3.1认识不等式

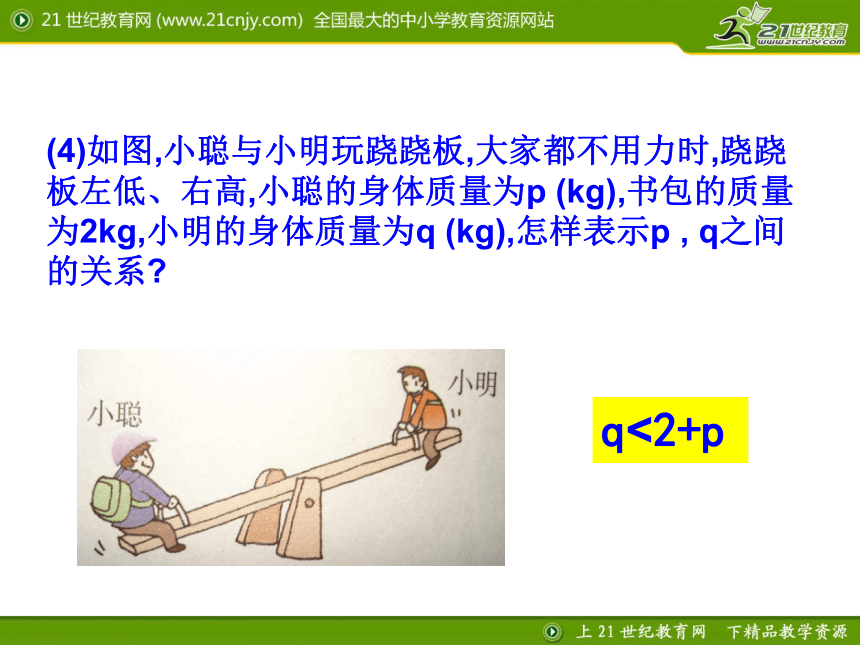
课件23张PPT。3.1 认识不等式下列问题中的数量关系应该用怎样的式子来表示:(1)如图,是从分水到瑶琳的公路上对汽车的限速标志,表示汽车在该路段行驶的速度不得超过40km/h,用v (km/h)表示汽车的速度,怎样表示v与40之间的关系?v≤40（2）根据科学家测定,太阳表面的温度不低于6000℃。设太阳表面的温度为t(℃)，怎样表示t和6000之间的关系?t 6000≥≥（3）天平左盘放3个乒乓球,右盘放5克砝码,天平倾斜,设每个乒乓球的质量为x(g),怎样表示x与5之间的关系?3x 5 ＞＞(4)如图,小聪与小明玩跷跷板,大家都不用力时,跷跷板左低、右高,小聪的身体质量为p (kg),书包的质量为2kg,小明的身体质量为q (kg),怎样表示p , q之间的关系?q<2+p（5）要使代数式 有意义, x的值与3之间有什么关系?x 3≠≠ 像v≤40，t≥6000，3x＞5，q＜p+2，x≠3这样，用符号“＜”（或“≤”），“＞”（或“≥”），“≠”连接而成的数学式子，叫不等式。这些用来连接的符号统称不等号。
像这样用“＞, ≥, ＜,≤, ≠”连接
而成的数学式子,叫做不等式. 这些用来连接的符号叫做不等号.辩一辩在数学表达式:
①x-2， ②-2<0，③4x+3y≤0， ④x+y=7
⑤x≠8，⑥x+y， ⑦x+4≥6， ⑧-2>8中，
不等式有______________________.试一试选择适当的不等号填空：
（1）2＿＿3； （2）－ ＿＿ －3
（3）－a2＿＿0
（4）若x≠y,则－x＿＿－y例1 根据下列数量关系列不等式：
（1）y的2倍与6的和比1小；
（2）x2减去10不大于10；
（3）设a，b，c为一个三角形的三条边长，两边
之和大于第三边.
（4）a是正数。2y+6<1x2-10≤10a+b>c a+c>b b+c>aa>0用不等式表示不等关系基本步骤是什么？（2）正确理解题中的关键词；（1）找准题中不等关系的两个量，并用代数式表示；（3）选择合适的不等号，连接两个代数式。题后反思比比看谁列得快又对（1） x比3大
（2） y与1的差小于y的45%
（3） y的绝对值与-8的和为负数
（4）正数a与1的和的算术平方根大于1
（5） x、y两数的平方和不小于0
（6） a与b的和的平方是非负数
练一练（1）x1=1，x2=2，请在数轴上表示出x1，x2的位置；（2）x＜1表示怎样的数的全体？据此理解， 表示怎样的数的全体？探索新知在数轴上表示下列不等式：（1）x<2（2）x ≥ -3（3）-2 ＜ x ≤1知识运用解：（1）（2）（3）在数轴上表示不等式，你认为需要确定什么？（2）确定方向；（1）确定空心圈或实心点；（3）注意选取合适的单位长度。题后反思看数轴写不等式○○●●①
②
③
④○x＞-3x＜2X≥ -2.5-3为x（m）。（1）用不等式表示发电机的正常工作的水位范围， 并把它表示在数轴上；解：（1）用不等式表示发电机的正常工作的水位范围是145 ≤ x≤ 175，在数轴上表示如图：（2）把X1=100, X2=125, X3=150, X4=165表示在数轴上显然，X3，X4满足不等式145 ≤ x≤ 175，而x1，x2不满足，
也就是说，当水位在150m，165m时，发电机能正常工作；
当水位在100m，125m时，发电机不能正常工作。课堂小结： 4、不等式是刻画不等量之间关系的重要模型，这一模型在
解决实际问题中起着重要的作用，体会建模思想和数形
结合的思想。　 实数a,b在数轴上的位置如图所示，选择适当的不等号填空：(1) a b
(2) |a| |b|
(3) a+b 0
(4) a-b 0
(5) ab 0我自信我能行＜＜＜＞＞ 下列不等式中，总能成立的是 （ ）
A． <0 B．
C．2a＞a D． ＞a
我自信我能行B≥0