2022-2023学年浙教版八年级数学上册 1.1 认识三角形 提升练习 (Word版含答案)
文档属性
| 名称 | 2022-2023学年浙教版八年级数学上册 1.1 认识三角形 提升练习 (Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 305.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-04 20:51:10 | ||
图片预览





文档简介
浙教版-8年级-上册-数学-第1章《三角形的初步知识》
1.1 认识三角形(1)
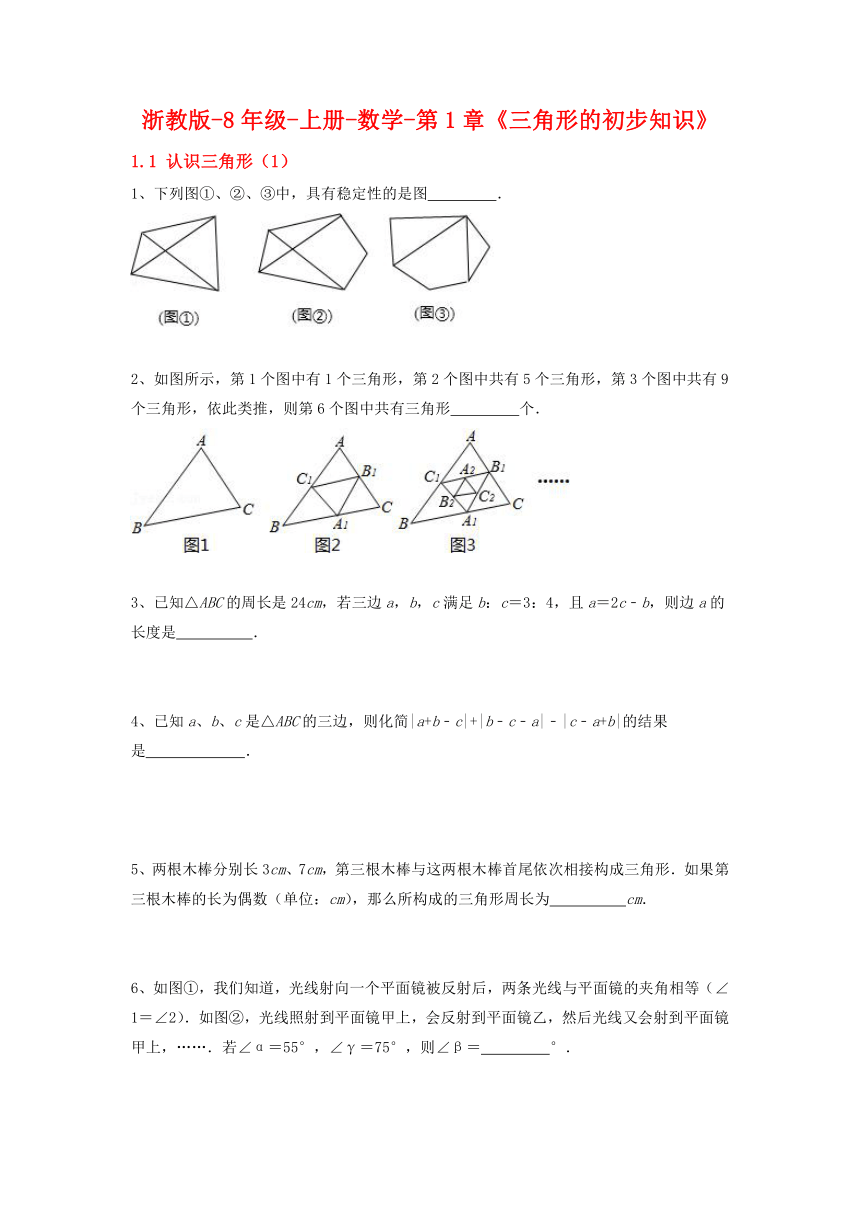
1、下列图①、②、③中,具有稳定性的是图 .
2、如图所示,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,依此类推,则第6个图中共有三角形 个.
3、已知△ABC的周长是24cm,若三边a,b,c满足b:c=3:4,且a=2c﹣b,则边a的长度是 .
4、已知a、b、c是△ABC的三边,则化简|a+b﹣c|+|b﹣c﹣a|﹣|c﹣a+b|的结果是 .
5、两根木棒分别长3cm、7cm,第三根木棒与这两根木棒首尾依次相接构成三角形.如果第三根木棒的长为偶数(单位:cm),那么所构成的三角形周长为 cm.
6、如图①,我们知道,光线射向一个平面镜被反射后,两条光线与平面镜的夹角相等(∠1=∠2).如图②,光线照射到平面镜甲上,会反射到平面镜乙,然后光线又会射到平面镜甲上,…….若∠α=55°,∠γ=75°,则∠β= °.
7、已知△ABC中,∠A=65°,将∠B、∠C按照如图所示折叠,若∠ADB′=35°,则∠1+∠2+∠3= °.
8、如图,△ABC中,A1,A2,A3,…,An为AC边上不同的n个点,首先连接BA1,图中出现了3个不同的三角形,再连接BA2,图中便有6个不同的三角形…
(1)完成下表:
连接个数
出现三角形个数
(2)若出现了45个三角形,则共连接了多少个点?
(3)若一直连接到An,则图中共有 个三角形.
9、在同一平面内,用3根和5根火柴棒不折断首尾顺次相接,分别摆成三角形,现把这两个三角形根据三边火柴根数分别记为(1,1,1)和(2,2,1).
(1)现有12根火柴,请你摆一摆,分别画出符合条件的所有三角形,并标出各边三角形的火柴根数?
(2)如果有18根火柴,你能摆成几种三角形?请按题中的记法表示出所有符合条件的三角形.(不要求画图)
10、过A、B、C、D、E五个点中任意三点画三角形;
(1)其中以AB为一边可以画出 个三角形;
(2)其中以C为顶点可以画出 个三角形.
11、① 设△ABC的三边分别为a、b、c,试证明:a<(a+b+c)
② 设四边形的四边长依次为a、b、c、d,两条对角线分别为e、f,证明:e+f>(a+b+c+d)
12、如图,点P是△ABC内部的一点.
(1)度量线段AB,AC,PB,PC的长度,根据度量结果比较AB+AC与PB+PC的大小;
(2)改变点P的位置,上述结论还成立吗?
(3)你能说明上述结论为什么正确吗?
13、如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:
(1)∠BAE的度数; (2)∠DAE的度数;
(3)探究:小明认为如果条件∠B=70°,∠C=30°改成∠B﹣∠C=40°,也能得出∠DAE的度数?
若能,请你写出求解过程;若不能,请说明理由.
14、在△ABC中,D是BC边上一点,且∠CDA=∠CAB,MN是经过点D的一条直线.
(1)直线MN⊥AC,垂足为点E,在图1中画出直线MN.若∠CAB=70°,∠DAB=20°,求∠CAD,∠CDE的度数;
(2)直线MN∥AB交AC边于点F,在图2中画出直线MN,求证:∠CDF=∠CAD.(提示:三角形内角和等于180°)
15、问题情境:如图1,AB∥CD,∠PAB=120°,∠PCD=130°,求∠APC的度数.小明的思路是:过点P作PE∥AB,通过平行线性质来求∠APC.
(1)问题思考:按小明的思路,请你求出∠APC的度数;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B,D两点之间运动时,请你判断∠APC与α,β之间有何数量关系,并说明你的理由;
(3)问题解决:我们发现借助构造平行线的方法可以解决许多问题,随着以后的学习你还会发现平行线的许多用途.请你试试构造平行线解决以下问题.
已知:如图3,三角形ABC,求证:∠A+∠B+∠C=180°.
16、小红同学以“一个含30°的直角三角尺和两条平行线”为背景开展探究活动.如图,在直角三角形ABC中,已知∠BAC=90°,∠ABC=30°,∠ACB=60°,直线a∥b.
(1)如图1,直线b与线段AC相交(b不过点C),若∠1=43°,求∠2的度数;
(2)如图2,小红同学把直线b向上平移,使得直线b过点C,若∠1=43°,求∠2的度数;
(3)如用3,小红同学把直线b继续向上平移,使得直线b与线段BC相交(b不过点B),设∠1=x(30°<x<90°),∠2=y,求y与x之间的关系式.
1.1 认识三角形(1)-参考答案
1、下列图①、②、③中,具有稳定性的是图 .
【解答】解:∵三角形具有稳定性,∴①具有稳定性.
2、如图所示,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,依此类推,则第6个图中共有三角形 个.
【解答】解:第n个图形中,三角形的个数是1+4(n﹣1)=4n﹣3.所以当n=6时,原式=21.
3、已知△ABC的周长是24cm,若三边a,b,c满足b:c=3:4,且a=2c﹣b,则边a的长度是 .
【解答】解:由题意得,,解得:,故答案为:10cm.
4、已知a、b、c是△ABC的三边,则化简|a+b﹣c|+|b﹣c﹣a|﹣|c﹣a+b|的结果是 .
【解答】解:∵a、b、c分别为△ABC的三边长,∴a+b﹣c>0,b﹣c﹣a<0,c﹣a+b>0,
∴|a+b﹣c|+|b﹣c﹣a|﹣|c﹣a+b|=a+b﹣c﹣b+c+a﹣c+a﹣b=3a﹣b﹣c.故答案为:3a﹣b﹣c.
5、两根木棒分别长3cm、7cm,第三根木棒与这两根木棒首尾依次相接构成三角形.如果第三根木棒的长为偶数(单位:cm),那么所构成的三角形周长为 cm.
【解答】解:根据三角形的三边关系,得第三根木棒的长大于4cm而小于10cm.
又第三根木棒的长是偶数,则应为6cm,8cm.∴所构成的三角形周长为16cm或18cm,故答案为:16或18.
6、如图①,我们知道,光线射向一个平面镜被反射后,两条光线与平面镜的夹角相等(∠1=∠2).如图②,光线照射到平面镜甲上,会反射到平面镜乙,然后光线又会射到平面镜甲上,…….若∠α=55°,∠γ=75°,则∠β= °.
【解答】解:如图,由题意知:∠α=∠1=55°,∠β=∠2,∠γ=∠3=75°,
∵∠1+∠3+∠4=180°,∴∠4=50°,∵∠2+∠4+∠β=180°,∴∠β=65°,故答案为:65.
7、已知△ABC中,∠A=65°,将∠B、∠C按照如图所示折叠,若∠ADB′=35°,则∠1+∠2+∠3= °.
【解答】解:由折叠知:∠B=∠B′,∠C=∠C′.∵∠3=∠B+∠4,∠4=∠ADB′+∠B′,
∴∠3=∠B+∠ADB′+∠B′=2∠B+35°.
∵∠1+∠2=180°﹣∠C′GC+180°﹣∠C′FC=360°﹣(∠C′FC+∠C′GC),
∠C′FC+∠C′GC=360°﹣∠C﹣∠C′=360°﹣2∠C,
∴∠1+∠2=360°﹣(∠C′FC+∠C′GC)=360°﹣(360°﹣2∠C)=2∠C.
∴∠1+∠2+∠3=2∠C+2∠B+35°=2(∠C+∠B)+35°=2(180°﹣∠A)+35°=2(180°﹣65°)+35°=265°
故答案为:265°.
8、如图,△ABC中,A1,A2,A3,…,An为AC边上不同的n个点,首先连接BA1,图中出现了3个不同的三角形,再连接BA2,图中便有6个不同的三角形…
(1)完成下表:
连接个数
出现三角形个数
(2)若出现了45个三角形,则共连接了多少个点?
(3)若一直连接到An,则图中共有 个三角形.
【解答】解:(1)
连接个数 1 2 3 4 5 6
出现三角形个数 3 6 10 15 21 28
(2)8个点;
(3)1+2+3+…+(n+1)=[1+2+3+…+(n+1)+1+2+3+…+(n+1)]=(n+1)(n+2).
9、在同一平面内,用3根和5根火柴棒不折断首尾顺次相接,分别摆成三角形,现把这两个三角形根据三边火柴根数分别记为(1,1,1)和(2,2,1).
(1)现有12根火柴,请你摆一摆,分别画出符合条件的所有三角形,并标出各边三角形的火柴根数?
(2)如果有18根火柴,你能摆成几种三角形?请按题中的记法表示出所有符合条件的三角形.(不要求画图)
【解答】解:(1)根据边长都为正数和周长为12,以及三角形边长的关系可得出所有的符合条件的三角形分别为(2,5,5),(3,4,5),(4,4,4);
(2)(2,8,8),(3,7,8),(4,7,7),(4,6,8),(5,6,7),(5,5,8),(6,6,6).
10、过A、B、C、D、E五个点中任意三点画三角形;
(1)其中以AB为一边可以画出 个三角形;
(2)其中以C为顶点可以画出 个三角形.
【解答】解:(1)如图,以AB为一边的三角形有△ABC、△ABD、△ABE共3个;
(2)如图,以点C为顶点的三角形有△ABC、△BEC、△BCD、△ACE、△ACD、△CDE共6个.
11、① 设△ABC的三边分别为a、b、c,试证明:a<(a+b+c)
② 设四边形的四边长依次为a、b、c、d,两条对角线分别为e、f,证明:e+f>(a+b+c+d)
【解答】解:①证明:∵b+c>a,∴b+c>a,∴b+c+a>a+a,
∴(a+b+c)>a,即a<(a+b+c);
② 证明:显然n+x>a,x+m>b,y+m>c,n+y>d,所以:2(x+y+m+n)>a+b+c+d,
即:2(e+f)>a+b+c+d,所以:e+f>(a+b+c+d).
12、如图,点P是△ABC内部的一点.
(1)度量线段AB,AC,PB,PC的长度,根据度量结果比较AB+AC与PB+PC的大小;
(2)改变点P的位置,上述结论还成立吗?
(3)你能说明上述结论为什么正确吗?
【解答】解:(1)如图有:AB+AC>PB+PC;
(2)改变点P的位置,上述结论还成立;
(3)如图,连接AP,BP,CP,延长BP交于AC于点E,
在△ABE中有,AB+AE>BE=BP+PE①,在△CEP中有,PE+CE>PC②
①+②得,AB+AE+PE+CE>BP+PE+PC,AB+AC+PE>BP+PE+PC,∴AB+AC>BP+PC.
13、如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:
(1)∠BAE的度数; (2)∠DAE的度数;
(3)探究:小明认为如果条件∠B=70°,∠C=30°改成∠B﹣∠C=40°,也能得出∠DAE的度数?
若能,请你写出求解过程;若不能,请说明理由.
【解答】解:(1)∵∠B+∠C+∠BAC=180°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣70°﹣30°=80°,
∵AE平分∠BAC,∴∠BAE=∠BAC=40°;
(2)∵AD⊥BC,∴∠ADE=90°,而∠ADE=∠B+∠BAD,∴∠BAD=90°﹣∠B=90°﹣70°=20°,
∴∠DAE=∠BAE﹣∠BAD=40°﹣20°=20°;
(3)能.∵∠B+∠C+∠BAC=180°,∴∠BAC=180°﹣∠B﹣∠C,∵AE平分∠BAC,
∴∠BAE=∠BAC=(180°﹣∠B﹣∠C)=90°﹣(∠B+∠C),∵AD⊥BC,∴∠ADE=90°,
而∠ADE=∠B+∠BAD,∴∠BAD=90°﹣∠B,
∴∠DAE=∠BAE﹣∠BAD=90°﹣(∠B+∠C)﹣(90°﹣∠B)=(∠B﹣∠C),
∵∠B﹣∠C=40°,∴∠DAE=×40°=20°.
14、在△ABC中,D是BC边上一点,且∠CDA=∠CAB,MN是经过点D的一条直线.
(1)直线MN⊥AC,垂足为点E,在图1中画出直线MN.若∠CAB=70°,∠DAB=20°,求∠CAD,∠CDE的度数;
(2)直线MN∥AB交AC边于点F,在图2中画出直线MN,求证:∠CDF=∠CAD.(提示:三角形内角和等于180°)
【解答】解:(1)如图1中,∵∠CAB=70°,∠DAB=20°,∴∠CAD=∠CAB﹣∠DAB=70°﹣20°=50°,
∵DE⊥AC,∴∠AED=90°,∴∠ADE=90°﹣50°=40°,∵∠ADC=∠CAB=70°,
∴∠CDE=∠ADC﹣∠ADE=70°﹣40°=30°;
(2)证明:∵MN∥AB,∴∠ADF=∠DAB,∵∠ADC=∠CAB,∴∠CDF=∠CAD.
15、问题情境:如图1,AB∥CD,∠PAB=120°,∠PCD=130°,求∠APC的度数.小明的思路是:过点P作PE∥AB,通过平行线性质来求∠APC.
(1)问题思考:按小明的思路,请你求出∠APC的度数;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B,D两点之间运动时,请你判断∠APC与α,β之间有何数量关系,并说明你的理由;
(3)问题解决:我们发现借助构造平行线的方法可以解决许多问题,随着以后的学习你还会发现平行线的许多用途.请你试试构造平行线解决以下问题.
已知:如图3,三角形ABC,求证:∠A+∠B+∠C=180°.
【解答】解:(1)如图1,过P作PE∥AB,∵AB∥CD,∴PE∥AB∥CD,
∴∠PAB+∠APE=180°,∠PCD+∠CPE=180°,∵∠PAB=120°,∠PCD=130°,
∴∠APE=60°,∠CPE=50°,∴∠APC=∠APE+∠CPE=110°;
(2)∠APC=α+β,理由如下:如图2,过P作PE∥AB,交AC于E,∵AB∥CD,∴AB∥PE∥CD,
∴∠APE=∠PAB=α,∠CPE=∠PCD=β,∴∠APC=∠APE+∠CPE=α+β,
(3)证明:如图3,过点A作MN∥BC,∴∠B=∠1,∠C=∠2,∵∠BAC+∠1+∠2=180°,∴∠BAC+∠B+∠C=180°.
16、小红同学以“一个含30°的直角三角尺和两条平行线”为背景开展探究活动.如图,在直角三角形ABC中,已知∠BAC=90°,∠ABC=30°,∠ACB=60°,直线a∥b.
(1)如图1,直线b与线段AC相交(b不过点C),若∠1=43°,求∠2的度数;
(2)如图2,小红同学把直线b向上平移,使得直线b过点C,若∠1=43°,求∠2的度数;
(3)如用3,小红同学把直线b继续向上平移,使得直线b与线段BC相交(b不过点B),设∠1=x(30°<x<90°),∠2=y,求y与x之间的关系式.
【解答】解:(1)如图(1),∵∠BAC=90°,∠1=43°,∴∠3=180°﹣∠BAC﹣∠1=47°,
∵a∥b,∴∠2=∠3=47°;
(2)如图(2),∵a∥b,∠1=43°,∴∠3=∠1=43°,
∴∠4=∠3﹣∠ABC=13°,∴∠2=180°﹣∠4=167°;
(3)如图(3),∵a∥b,∠1=x,∴∠3=∠1=x,∴∠4=∠3﹣∠ABC=x﹣30°,
∴∠2=180°﹣∠4=210°﹣x,即y=210°﹣x.
1.1 认识三角形(1)
1、下列图①、②、③中,具有稳定性的是图 .
2、如图所示,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,依此类推,则第6个图中共有三角形 个.
3、已知△ABC的周长是24cm,若三边a,b,c满足b:c=3:4,且a=2c﹣b,则边a的长度是 .
4、已知a、b、c是△ABC的三边,则化简|a+b﹣c|+|b﹣c﹣a|﹣|c﹣a+b|的结果是 .
5、两根木棒分别长3cm、7cm,第三根木棒与这两根木棒首尾依次相接构成三角形.如果第三根木棒的长为偶数(单位:cm),那么所构成的三角形周长为 cm.
6、如图①,我们知道,光线射向一个平面镜被反射后,两条光线与平面镜的夹角相等(∠1=∠2).如图②,光线照射到平面镜甲上,会反射到平面镜乙,然后光线又会射到平面镜甲上,…….若∠α=55°,∠γ=75°,则∠β= °.
7、已知△ABC中,∠A=65°,将∠B、∠C按照如图所示折叠,若∠ADB′=35°,则∠1+∠2+∠3= °.
8、如图,△ABC中,A1,A2,A3,…,An为AC边上不同的n个点,首先连接BA1,图中出现了3个不同的三角形,再连接BA2,图中便有6个不同的三角形…
(1)完成下表:
连接个数
出现三角形个数
(2)若出现了45个三角形,则共连接了多少个点?
(3)若一直连接到An,则图中共有 个三角形.
9、在同一平面内,用3根和5根火柴棒不折断首尾顺次相接,分别摆成三角形,现把这两个三角形根据三边火柴根数分别记为(1,1,1)和(2,2,1).
(1)现有12根火柴,请你摆一摆,分别画出符合条件的所有三角形,并标出各边三角形的火柴根数?
(2)如果有18根火柴,你能摆成几种三角形?请按题中的记法表示出所有符合条件的三角形.(不要求画图)
10、过A、B、C、D、E五个点中任意三点画三角形;
(1)其中以AB为一边可以画出 个三角形;
(2)其中以C为顶点可以画出 个三角形.
11、① 设△ABC的三边分别为a、b、c,试证明:a<(a+b+c)
② 设四边形的四边长依次为a、b、c、d,两条对角线分别为e、f,证明:e+f>(a+b+c+d)
12、如图,点P是△ABC内部的一点.
(1)度量线段AB,AC,PB,PC的长度,根据度量结果比较AB+AC与PB+PC的大小;
(2)改变点P的位置,上述结论还成立吗?
(3)你能说明上述结论为什么正确吗?
13、如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:
(1)∠BAE的度数; (2)∠DAE的度数;
(3)探究:小明认为如果条件∠B=70°,∠C=30°改成∠B﹣∠C=40°,也能得出∠DAE的度数?
若能,请你写出求解过程;若不能,请说明理由.
14、在△ABC中,D是BC边上一点,且∠CDA=∠CAB,MN是经过点D的一条直线.
(1)直线MN⊥AC,垂足为点E,在图1中画出直线MN.若∠CAB=70°,∠DAB=20°,求∠CAD,∠CDE的度数;
(2)直线MN∥AB交AC边于点F,在图2中画出直线MN,求证:∠CDF=∠CAD.(提示:三角形内角和等于180°)
15、问题情境:如图1,AB∥CD,∠PAB=120°,∠PCD=130°,求∠APC的度数.小明的思路是:过点P作PE∥AB,通过平行线性质来求∠APC.
(1)问题思考:按小明的思路,请你求出∠APC的度数;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B,D两点之间运动时,请你判断∠APC与α,β之间有何数量关系,并说明你的理由;
(3)问题解决:我们发现借助构造平行线的方法可以解决许多问题,随着以后的学习你还会发现平行线的许多用途.请你试试构造平行线解决以下问题.
已知:如图3,三角形ABC,求证:∠A+∠B+∠C=180°.
16、小红同学以“一个含30°的直角三角尺和两条平行线”为背景开展探究活动.如图,在直角三角形ABC中,已知∠BAC=90°,∠ABC=30°,∠ACB=60°,直线a∥b.
(1)如图1,直线b与线段AC相交(b不过点C),若∠1=43°,求∠2的度数;
(2)如图2,小红同学把直线b向上平移,使得直线b过点C,若∠1=43°,求∠2的度数;
(3)如用3,小红同学把直线b继续向上平移,使得直线b与线段BC相交(b不过点B),设∠1=x(30°<x<90°),∠2=y,求y与x之间的关系式.
1.1 认识三角形(1)-参考答案
1、下列图①、②、③中,具有稳定性的是图 .
【解答】解:∵三角形具有稳定性,∴①具有稳定性.
2、如图所示,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,依此类推,则第6个图中共有三角形 个.
【解答】解:第n个图形中,三角形的个数是1+4(n﹣1)=4n﹣3.所以当n=6时,原式=21.
3、已知△ABC的周长是24cm,若三边a,b,c满足b:c=3:4,且a=2c﹣b,则边a的长度是 .
【解答】解:由题意得,,解得:,故答案为:10cm.
4、已知a、b、c是△ABC的三边,则化简|a+b﹣c|+|b﹣c﹣a|﹣|c﹣a+b|的结果是 .
【解答】解:∵a、b、c分别为△ABC的三边长,∴a+b﹣c>0,b﹣c﹣a<0,c﹣a+b>0,
∴|a+b﹣c|+|b﹣c﹣a|﹣|c﹣a+b|=a+b﹣c﹣b+c+a﹣c+a﹣b=3a﹣b﹣c.故答案为:3a﹣b﹣c.
5、两根木棒分别长3cm、7cm,第三根木棒与这两根木棒首尾依次相接构成三角形.如果第三根木棒的长为偶数(单位:cm),那么所构成的三角形周长为 cm.
【解答】解:根据三角形的三边关系,得第三根木棒的长大于4cm而小于10cm.
又第三根木棒的长是偶数,则应为6cm,8cm.∴所构成的三角形周长为16cm或18cm,故答案为:16或18.
6、如图①,我们知道,光线射向一个平面镜被反射后,两条光线与平面镜的夹角相等(∠1=∠2).如图②,光线照射到平面镜甲上,会反射到平面镜乙,然后光线又会射到平面镜甲上,…….若∠α=55°,∠γ=75°,则∠β= °.
【解答】解:如图,由题意知:∠α=∠1=55°,∠β=∠2,∠γ=∠3=75°,
∵∠1+∠3+∠4=180°,∴∠4=50°,∵∠2+∠4+∠β=180°,∴∠β=65°,故答案为:65.
7、已知△ABC中,∠A=65°,将∠B、∠C按照如图所示折叠,若∠ADB′=35°,则∠1+∠2+∠3= °.
【解答】解:由折叠知:∠B=∠B′,∠C=∠C′.∵∠3=∠B+∠4,∠4=∠ADB′+∠B′,
∴∠3=∠B+∠ADB′+∠B′=2∠B+35°.
∵∠1+∠2=180°﹣∠C′GC+180°﹣∠C′FC=360°﹣(∠C′FC+∠C′GC),
∠C′FC+∠C′GC=360°﹣∠C﹣∠C′=360°﹣2∠C,
∴∠1+∠2=360°﹣(∠C′FC+∠C′GC)=360°﹣(360°﹣2∠C)=2∠C.
∴∠1+∠2+∠3=2∠C+2∠B+35°=2(∠C+∠B)+35°=2(180°﹣∠A)+35°=2(180°﹣65°)+35°=265°
故答案为:265°.
8、如图,△ABC中,A1,A2,A3,…,An为AC边上不同的n个点,首先连接BA1,图中出现了3个不同的三角形,再连接BA2,图中便有6个不同的三角形…
(1)完成下表:
连接个数
出现三角形个数
(2)若出现了45个三角形,则共连接了多少个点?
(3)若一直连接到An,则图中共有 个三角形.
【解答】解:(1)
连接个数 1 2 3 4 5 6
出现三角形个数 3 6 10 15 21 28
(2)8个点;
(3)1+2+3+…+(n+1)=[1+2+3+…+(n+1)+1+2+3+…+(n+1)]=(n+1)(n+2).
9、在同一平面内,用3根和5根火柴棒不折断首尾顺次相接,分别摆成三角形,现把这两个三角形根据三边火柴根数分别记为(1,1,1)和(2,2,1).
(1)现有12根火柴,请你摆一摆,分别画出符合条件的所有三角形,并标出各边三角形的火柴根数?
(2)如果有18根火柴,你能摆成几种三角形?请按题中的记法表示出所有符合条件的三角形.(不要求画图)
【解答】解:(1)根据边长都为正数和周长为12,以及三角形边长的关系可得出所有的符合条件的三角形分别为(2,5,5),(3,4,5),(4,4,4);
(2)(2,8,8),(3,7,8),(4,7,7),(4,6,8),(5,6,7),(5,5,8),(6,6,6).
10、过A、B、C、D、E五个点中任意三点画三角形;
(1)其中以AB为一边可以画出 个三角形;
(2)其中以C为顶点可以画出 个三角形.
【解答】解:(1)如图,以AB为一边的三角形有△ABC、△ABD、△ABE共3个;
(2)如图,以点C为顶点的三角形有△ABC、△BEC、△BCD、△ACE、△ACD、△CDE共6个.
11、① 设△ABC的三边分别为a、b、c,试证明:a<(a+b+c)
② 设四边形的四边长依次为a、b、c、d,两条对角线分别为e、f,证明:e+f>(a+b+c+d)
【解答】解:①证明:∵b+c>a,∴b+c>a,∴b+c+a>a+a,
∴(a+b+c)>a,即a<(a+b+c);
② 证明:显然n+x>a,x+m>b,y+m>c,n+y>d,所以:2(x+y+m+n)>a+b+c+d,
即:2(e+f)>a+b+c+d,所以:e+f>(a+b+c+d).
12、如图,点P是△ABC内部的一点.
(1)度量线段AB,AC,PB,PC的长度,根据度量结果比较AB+AC与PB+PC的大小;
(2)改变点P的位置,上述结论还成立吗?
(3)你能说明上述结论为什么正确吗?
【解答】解:(1)如图有:AB+AC>PB+PC;
(2)改变点P的位置,上述结论还成立;
(3)如图,连接AP,BP,CP,延长BP交于AC于点E,
在△ABE中有,AB+AE>BE=BP+PE①,在△CEP中有,PE+CE>PC②
①+②得,AB+AE+PE+CE>BP+PE+PC,AB+AC+PE>BP+PE+PC,∴AB+AC>BP+PC.
13、如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:
(1)∠BAE的度数; (2)∠DAE的度数;
(3)探究:小明认为如果条件∠B=70°,∠C=30°改成∠B﹣∠C=40°,也能得出∠DAE的度数?
若能,请你写出求解过程;若不能,请说明理由.
【解答】解:(1)∵∠B+∠C+∠BAC=180°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣70°﹣30°=80°,
∵AE平分∠BAC,∴∠BAE=∠BAC=40°;
(2)∵AD⊥BC,∴∠ADE=90°,而∠ADE=∠B+∠BAD,∴∠BAD=90°﹣∠B=90°﹣70°=20°,
∴∠DAE=∠BAE﹣∠BAD=40°﹣20°=20°;
(3)能.∵∠B+∠C+∠BAC=180°,∴∠BAC=180°﹣∠B﹣∠C,∵AE平分∠BAC,
∴∠BAE=∠BAC=(180°﹣∠B﹣∠C)=90°﹣(∠B+∠C),∵AD⊥BC,∴∠ADE=90°,
而∠ADE=∠B+∠BAD,∴∠BAD=90°﹣∠B,
∴∠DAE=∠BAE﹣∠BAD=90°﹣(∠B+∠C)﹣(90°﹣∠B)=(∠B﹣∠C),
∵∠B﹣∠C=40°,∴∠DAE=×40°=20°.
14、在△ABC中,D是BC边上一点,且∠CDA=∠CAB,MN是经过点D的一条直线.
(1)直线MN⊥AC,垂足为点E,在图1中画出直线MN.若∠CAB=70°,∠DAB=20°,求∠CAD,∠CDE的度数;
(2)直线MN∥AB交AC边于点F,在图2中画出直线MN,求证:∠CDF=∠CAD.(提示:三角形内角和等于180°)
【解答】解:(1)如图1中,∵∠CAB=70°,∠DAB=20°,∴∠CAD=∠CAB﹣∠DAB=70°﹣20°=50°,
∵DE⊥AC,∴∠AED=90°,∴∠ADE=90°﹣50°=40°,∵∠ADC=∠CAB=70°,
∴∠CDE=∠ADC﹣∠ADE=70°﹣40°=30°;
(2)证明:∵MN∥AB,∴∠ADF=∠DAB,∵∠ADC=∠CAB,∴∠CDF=∠CAD.
15、问题情境:如图1,AB∥CD,∠PAB=120°,∠PCD=130°,求∠APC的度数.小明的思路是:过点P作PE∥AB,通过平行线性质来求∠APC.
(1)问题思考:按小明的思路,请你求出∠APC的度数;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B,D两点之间运动时,请你判断∠APC与α,β之间有何数量关系,并说明你的理由;
(3)问题解决:我们发现借助构造平行线的方法可以解决许多问题,随着以后的学习你还会发现平行线的许多用途.请你试试构造平行线解决以下问题.
已知:如图3,三角形ABC,求证:∠A+∠B+∠C=180°.
【解答】解:(1)如图1,过P作PE∥AB,∵AB∥CD,∴PE∥AB∥CD,
∴∠PAB+∠APE=180°,∠PCD+∠CPE=180°,∵∠PAB=120°,∠PCD=130°,
∴∠APE=60°,∠CPE=50°,∴∠APC=∠APE+∠CPE=110°;
(2)∠APC=α+β,理由如下:如图2,过P作PE∥AB,交AC于E,∵AB∥CD,∴AB∥PE∥CD,
∴∠APE=∠PAB=α,∠CPE=∠PCD=β,∴∠APC=∠APE+∠CPE=α+β,
(3)证明:如图3,过点A作MN∥BC,∴∠B=∠1,∠C=∠2,∵∠BAC+∠1+∠2=180°,∴∠BAC+∠B+∠C=180°.
16、小红同学以“一个含30°的直角三角尺和两条平行线”为背景开展探究活动.如图,在直角三角形ABC中,已知∠BAC=90°,∠ABC=30°,∠ACB=60°,直线a∥b.
(1)如图1,直线b与线段AC相交(b不过点C),若∠1=43°,求∠2的度数;
(2)如图2,小红同学把直线b向上平移,使得直线b过点C,若∠1=43°,求∠2的度数;
(3)如用3,小红同学把直线b继续向上平移,使得直线b与线段BC相交(b不过点B),设∠1=x(30°<x<90°),∠2=y,求y与x之间的关系式.
【解答】解:(1)如图(1),∵∠BAC=90°,∠1=43°,∴∠3=180°﹣∠BAC﹣∠1=47°,
∵a∥b,∴∠2=∠3=47°;
(2)如图(2),∵a∥b,∠1=43°,∴∠3=∠1=43°,
∴∠4=∠3﹣∠ABC=13°,∴∠2=180°﹣∠4=167°;
(3)如图(3),∵a∥b,∠1=x,∴∠3=∠1=x,∴∠4=∠3﹣∠ABC=x﹣30°,
∴∠2=180°﹣∠4=210°﹣x,即y=210°﹣x.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
