2021-2022学年浙教版八年级数学上册2.7 探索勾股定理 同步练习(word版含解析)
文档属性
| 名称 | 2021-2022学年浙教版八年级数学上册2.7 探索勾股定理 同步练习(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 445.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 00:00:00 | ||
图片预览


文档简介
浙教版八上(浙教版)第2章 特殊三角形2.7 探索勾股定理
一、选择题(共8小题)
1. 下列直角三角形中,以 为直角三角形斜边的是
A. ,, B. ,,
C. ,, D. ,,
2. 已知 的三边长分别是 ,,,则 的面积是
A. B. C. D.
3. 已知 ,, 为 的三边,且满足 ,则 是
A. 等边三角形 B. 直角三角形
C. 等腰直角三角形 D. 等腰三角形或直角三角形
4. 由下列条件不能判定 为直角三角形的是
A.
B.
C.
D. ,,
5. 如图所示,在单位正方形组成的网格图中标有 ,,, 四条线段,其中能构成一个直角三角形三边的线段是
A. ,, B. ,, C. ,, D. ,,
6. 在长方形 中,,, 为 ,, 边上的点,且 ,,,,,则 的长为
A. B. C. D.
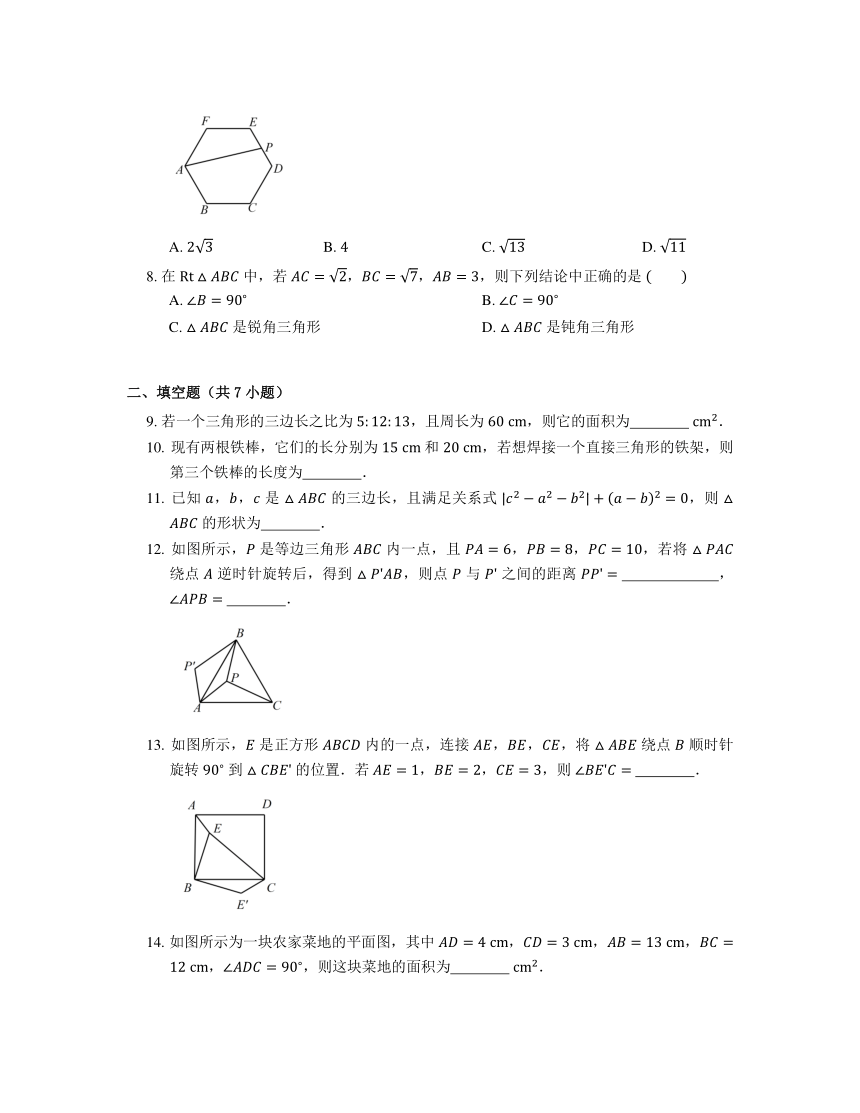
7. 如图所示,正六边形 中,, 是 的中点,连接 ,则 的长为
A. B. C. D.
8. 在 中,若 ,,,则下列结论中正确的是
A. B.
C. 是锐角三角形 D. 是钝角三角形
二、填空题(共7小题)
9. 若一个三角形的三边长之比为 ,且周长为 ,则它的面积为 .
10. 现有两根铁棒,它们的长分别为 和 ,若想焊接一个直接三角形的铁架,则第三个铁棒的长度为 .
11. 已知 ,, 是 的三边长,且满足关系式 ,则 的形状为 .
12. 如图所示, 是等边三角形 内一点,且 ,,,若将 绕点 逆时针旋转后,得到 ,则点 与 之间的距离 , .
13. 如图所示, 是正方形 内的一点,连接 ,,,将 绕点 顺时针旋转 到 的位置.若 ,,,则 .
14. 如图所示为一块农家菜地的平面图,其中 ,,,,,则这块菜地的面积为 .
15. 若 , , 是直角三角形的三条边长,斜边 上的高的长是 ,给出下列结论:
① 以 , , 的长为边的三条线段能组成一个三角形;
② 以 , , 的长为边的三条线段能组成一个三角形;
③ 以 , , 的长为边的三条线段能组成直角三角形;
④ 以 , , 的长为边的三条线段能组成直角三角形.
其中所有正确结论的序号为 .
三、解答题(共5小题)
16. 如图所示,在 的方格纸中,每一个小正方形的边长都为 .四边形 的顶点都在格点上.
(1) 是不是直角 请说明理由.
(2)求四边形 的面积(可以根据需要添加字母).
17. 已知三角形的三边分别为 ,,,且 ,,.
(1)请判断这个三角形的形状.
(2)试找出一组 ,,,使三角形的最小边不小于 ,另两边的差为 ,三边均为正整数.
18. 如图所示,在正方形 中,,,,请你判定 的形状,并说明理由.
19. 如图所示,在 中,,,, 为 边上的动点,点 从点 出发沿边 往点 运动,当运动到点 时停止,若设点 运动的时间为 ,点 运动的速度为每秒 个单位长度.
(1)当 时, , .
(2)当 时, 是直角三角形.
(3)当 为何值时, 是等腰三角形 请说明理由.
20. 王老师在一次探究性学习课程中,设计了如下数表:
(1)请你分别观察 ,, 与 之间的关系,并用含自然数 的代数式表示: , , .
(2)以 ,, 为边的三角形是否为直角三角形 证明你的结论.
(3)观察下列勾股数 ,,,,分析其中的规律,根据规律写出第五组勾股数.
答案
1. A
2. A
3. D
4. D
5. B
6. B
7. C
8. B
9.
10. 或
11. 等腰直角三角形
12. ,
13.
14.
15. ②③④
【解析】用特殊值法,取 , , ,则 ,分别代入四个答案排除.
16. (1) 是直角.理由如下:连接 .
,,,
.
是直角.
(2) ,
即四边形 的面积是 .
17. (1)
.
这个三角形是直角三角形.
(2) 取 ,即 ,
.
,.
18. 是直角三角形.理由如下:
在正方形 中,,,,
,,,.
,,.
.
,即 是直角三角形.
19. (1) ;
(2) 或
(3) ①当 时,如图1所示,过点 作 于点 ,
则 ,,
.
②当 时,,
.
③当 时,如图2所示,过点 作 于点 ,
则 .
,
.
综上所述, 时, 是等腰三角形.
20. (1) ;;.
(2) 是直角三角形.
证明:
,
,
.
以 ,, 为边的三角形是直角三角形.
(3) .
一、选择题(共8小题)
1. 下列直角三角形中,以 为直角三角形斜边的是
A. ,, B. ,,
C. ,, D. ,,
2. 已知 的三边长分别是 ,,,则 的面积是
A. B. C. D.
3. 已知 ,, 为 的三边,且满足 ,则 是
A. 等边三角形 B. 直角三角形
C. 等腰直角三角形 D. 等腰三角形或直角三角形
4. 由下列条件不能判定 为直角三角形的是
A.
B.
C.
D. ,,
5. 如图所示,在单位正方形组成的网格图中标有 ,,, 四条线段,其中能构成一个直角三角形三边的线段是
A. ,, B. ,, C. ,, D. ,,
6. 在长方形 中,,, 为 ,, 边上的点,且 ,,,,,则 的长为
A. B. C. D.
7. 如图所示,正六边形 中,, 是 的中点,连接 ,则 的长为
A. B. C. D.
8. 在 中,若 ,,,则下列结论中正确的是
A. B.
C. 是锐角三角形 D. 是钝角三角形
二、填空题(共7小题)
9. 若一个三角形的三边长之比为 ,且周长为 ,则它的面积为 .
10. 现有两根铁棒,它们的长分别为 和 ,若想焊接一个直接三角形的铁架,则第三个铁棒的长度为 .
11. 已知 ,, 是 的三边长,且满足关系式 ,则 的形状为 .
12. 如图所示, 是等边三角形 内一点,且 ,,,若将 绕点 逆时针旋转后,得到 ,则点 与 之间的距离 , .
13. 如图所示, 是正方形 内的一点,连接 ,,,将 绕点 顺时针旋转 到 的位置.若 ,,,则 .
14. 如图所示为一块农家菜地的平面图,其中 ,,,,,则这块菜地的面积为 .
15. 若 , , 是直角三角形的三条边长,斜边 上的高的长是 ,给出下列结论:
① 以 , , 的长为边的三条线段能组成一个三角形;
② 以 , , 的长为边的三条线段能组成一个三角形;
③ 以 , , 的长为边的三条线段能组成直角三角形;
④ 以 , , 的长为边的三条线段能组成直角三角形.
其中所有正确结论的序号为 .
三、解答题(共5小题)
16. 如图所示,在 的方格纸中,每一个小正方形的边长都为 .四边形 的顶点都在格点上.
(1) 是不是直角 请说明理由.
(2)求四边形 的面积(可以根据需要添加字母).
17. 已知三角形的三边分别为 ,,,且 ,,.
(1)请判断这个三角形的形状.
(2)试找出一组 ,,,使三角形的最小边不小于 ,另两边的差为 ,三边均为正整数.
18. 如图所示,在正方形 中,,,,请你判定 的形状,并说明理由.
19. 如图所示,在 中,,,, 为 边上的动点,点 从点 出发沿边 往点 运动,当运动到点 时停止,若设点 运动的时间为 ,点 运动的速度为每秒 个单位长度.
(1)当 时, , .
(2)当 时, 是直角三角形.
(3)当 为何值时, 是等腰三角形 请说明理由.
20. 王老师在一次探究性学习课程中,设计了如下数表:
(1)请你分别观察 ,, 与 之间的关系,并用含自然数 的代数式表示: , , .
(2)以 ,, 为边的三角形是否为直角三角形 证明你的结论.
(3)观察下列勾股数 ,,,,分析其中的规律,根据规律写出第五组勾股数.
答案
1. A
2. A
3. D
4. D
5. B
6. B
7. C
8. B
9.
10. 或
11. 等腰直角三角形
12. ,
13.
14.
15. ②③④
【解析】用特殊值法,取 , , ,则 ,分别代入四个答案排除.
16. (1) 是直角.理由如下:连接 .
,,,
.
是直角.
(2) ,
即四边形 的面积是 .
17. (1)
.
这个三角形是直角三角形.
(2) 取 ,即 ,
.
,.
18. 是直角三角形.理由如下:
在正方形 中,,,,
,,,.
,,.
.
,即 是直角三角形.
19. (1) ;
(2) 或
(3) ①当 时,如图1所示,过点 作 于点 ,
则 ,,
.
②当 时,,
.
③当 时,如图2所示,过点 作 于点 ,
则 .
,
.
综上所述, 时, 是等腰三角形.
20. (1) ;;.
(2) 是直角三角形.
证明:
,
,
.
以 ,, 为边的三角形是直角三角形.
(3) .
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
