2.3.1有理数的乘法 课件(共22张PPT)
文档属性
| 名称 | 2.3.1有理数的乘法 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
2.3有理数的乘法(1)
浙教版版七年级上册
教学目标
2.掌握有理数的乘法法则.
1.回顾小学所学数的乘法,经历乘法法则的发生过程.
3.会运用乘法法则求若干个有理数相乘的积.
4.理解倒数的概念.
复习回顾
正有理数
有理数
引入负数
运算
运算
2 × 3 = 6
2 × (3) =
(2 )× (3) =
(2 ) × 3 =
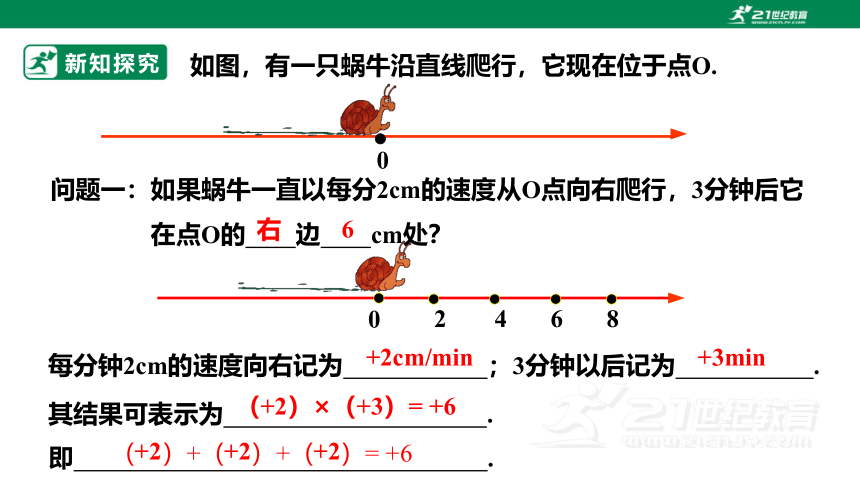
新知探究
如图,有一只蜗牛沿直线爬行,它现在位于点O.
0
0
2
4
6
8
每分钟2cm的速度向右记为 ;3分钟以后记为 .
其结果可表示为 .
+2cm/min
问题一:如果蜗牛一直以每分2cm的速度从O点向右爬行,3分钟后它
在点O的 边 cm处?
右
6
+3min
即 .
(+2)×(+3)= +6
( )+( )+( )= +6
+2 +2 +2
新知探究
其结果可表示为 .
0
8
6
4
2
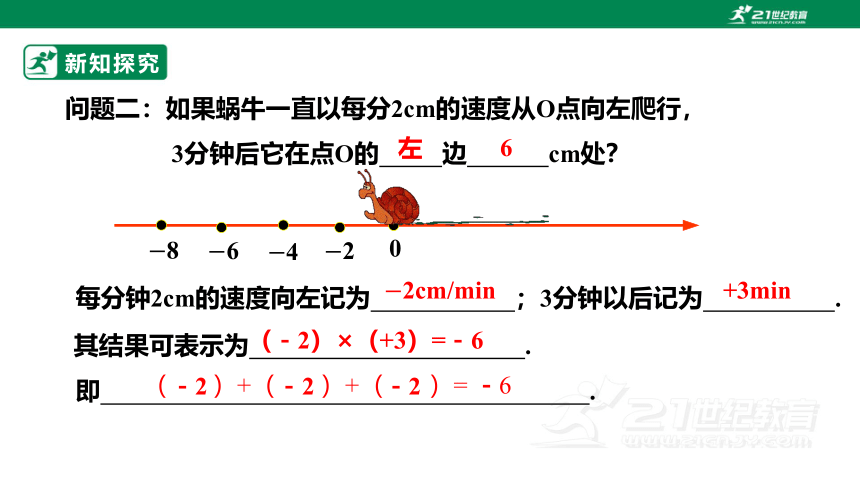
(-2)×(+3)=-6
问题二:如果蜗牛一直以每分2cm的速度从O点向左爬行,
3分钟后它在点O的 边 cm处?
左
6
每分钟2cm的速度向左记为 ;3分钟以后记为 .
2cm/min
+3min
即 .
( )+( )+( )= -6
-2 -2 -2
新知探究
问题三:如果蜗牛一直以每分2cm的速度向右爬行,现在蜗牛在O点处,
那么3分钟前它在点O的 边 cm处?
0
8
6
4
2
左
6
每分钟2cm的速度向右记为 ;3分钟前记为 .
2cm/min
3min
其结果可表示为 .
(+2)×( 3 )=-6
新知探究
问题四:如果蜗牛一直以每分2cm的速度向左爬行,现在蜗牛在O点处,
那么3分钟前它在点O的 边 cm处?
0
右
6
2
4
6
8
每分钟2cm的速度向左记为 ;3分钟前记为 .
2cm/min
3min
其结果可表示为 .
(2)×( 3 )
6
=
归纳总结
(+2)×(+3)= +6
(+2)×(3)=6
(2)×(+3)=6
比较算式,探寻运算规律
改变一个数的符号,积就变为原来的相反数.
(2)×(+3)= (2×3)= 6
(+2)×(3)= (2×3)=6
( 2 )×(3 )= +6
(2)×(3)= (2×3)= 6
改变两个数的符号,积就变为原来的数.
新知讲解
同号得正
异号得负
绝
对
值
相
乘
(+2)×(+3) =
+6
(-2 )×(-3) =
(+2 )×(-3) =
(-2 )×(+3) =
+6
-6
-6
0×(+3)=
0×(3)=
0
0
任何数同零相乘,积为零.
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数同零相乘,积为零.
牛刀小试
1、不计算,直接确定下列积的符号:
(1) 35×(-13) (2)(-14)×6
(3)(-7)×(-19) (4) 1.5×2.7
-
+
-
+
2、用“<”,“>”或“=”填空
(1)( 7)×(+3) 0. (2)( 13)×( 7.9) 0.
(3)0× ( ) 0. (4)(1) ×() ×(1.5)_____0.
<
>
=
<
典例精析
例1 : 计算:
(1)
(2)( 2.5)×4
(3)( 5)×0×
(4)( )×( 3)
(5)( 6)×( )×( 4)
=1
= (2.5×4)
= 10
=0
=+(×3)
=1
= (6××4)
= 30
几个有理数相乘,怎样确定积的符号?
多个不为零的有理数相乘,积的符号由负因数的个数确定.
负因数的个数为奇数时,积为负;负因数的个数为偶数时,积为正.
新知讲授
( )×( 3)
若两个有理数的乘积为1,就称这两个有理数互为倒数.
例如, 是 的倒数, 也是 的倒数.
练习: 的倒数是______ ,
8的倒数是______ ,
1的倒数是______ , 0的倒数是
1
7
0没有倒数
因为任何数与0相乘,积为0,不存在与0相乘积为1的数.
什么数的倒数是它本身?
1和1
要点提炼
注意事项
(1)0没有倒数.
(2)求分数的倒数,只要把这个分数的分子,分母颠倒位置即可.
(3)正数的倒数是正数,负数的倒数是负数.
(4)求小数的倒数时,要先把小数化成分数.
(5)求带分数的倒数时,要先把带分数化成假分数.
试探寻下列数的倒数
1 0.2 3 1 1
倒数
7
0
不存在
1
1
5
课堂练习
1、下列各式中,积为负数的是 ( )
A. (-5)×(-2)×(-3)×(-7) B. (-5)×(-2)×|-3|
C. (-5)×2×0×(-7) D. (-5)×2×(-3)×(-7)
2、下列关系式正确的是 ( )
A. |-3|<0 B. -(-3)<0 C. -3+2>0 D. -3×2<0
3、若|x|=4,|y|=7,且xy<0,则x+y的值为 ( )
A. 11或-11 B. 3或-3 C. 11或3 D. -11或-3
4、两个有理数的和为正数,积为负数,则这两个有理数是 ( )
A. 两个正数 B. 两个负数
C. 一正一负且正数的绝对值较大 D. 一正一负且负数的绝对值较大
D
D
B
C
5、下列说法中,正确的是 ( )
A. 0的倒数是0 B. 倒数是它本身的数是1
C. 相反数等于它本身的数是负数 D. 绝对值最小的数是0
D
6、计算:
(1)
(3)
(2)
(4)( 2)×3×( 0.5)
(6)( )×( )×( 2)
(5)| 1.25|×( 8)×4
=
=
=
=3
=
= 40
7、把 6表示成两个整数的积,有多少种可能?把它们全部写出来.
1
8、在数5,1,,5,中任取三个数相乘,其中最大的积是a,最小的积是b,求a,b的值.
a=5(4) 5=100
b=5(4) () =
课堂总结
通过本节课的交流,你有什么体验或收获
1.两数相乘,同号得 ,异号得 ,再把绝对值相乘;
0 乘任何数得 .
正
负
0
2.几个有理数相乘,因数都不为 0 时,
积的符号由 确定.
负因数的个数
奇数个为负,偶数个为正
有一因数为 0 时,积是
0 .
3. 倒数的定义
若两个有理数的乘积为1,就称这两个有理数互为倒数.
作业布置
1.作业本
2.教材练习题
拓展提升
1、若|a|=3, |b|=5,则a×b=________________.
2、已知a,b 互为相反数, c,d 互为倒数, m 的绝对值为2,
求 (a+b)c×d+m的值.
15或15
∵ a,b 互为相反数, c,d 互为倒数, m 的绝对值为2
∴ a+b = 0 ,c×d = 1, m = 2
∴ (a+b)c×d+m= 0+1+m = 3或1
3、若定义一种新的运算“*”,规定有理数a*b=4ab,如2*3=4×2×3=24.
(1)求3*(4)的值; (2)求(2)*(6*3)的值.
(1)3*(4)=4×3×(4)=48;
(2)(2)*(6*3)=(2)*(4×6×3)=(2)*(72)=4×(2)×(72)=576.
解:
趣味数学
如图,A,B两点在数轴上对应的数分别为a,b,且点A在点B的左边,|a|=10,|b|=90,a×b<0.
(1)求a,b的值.
(2)现有一只电子蚂蚁P从点A出发,以3个单位长度/秒的速度向右运动,同时另一只电子蚂蚁Q从点B出发,以2个单位长度/秒的速度向左运动.
①设两只电子蚂蚁在数轴上的点C相遇,求出点C对应的数是多少.
②经过多长时间,两只电子蚂蚁在数轴上相距20个单位长度?
板书设计
2.3有理数的乘法(1)
1.乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数与零相乘,积为零.
2.多个不为零的有理数相乘,积的符号由负因数的个数确定.
负因数的个数为奇数时,积为负;负因数的个数为偶数时,积为正.
若两个有理数的乘积为1,就称这两个有理数互为倒数.
3.倒数的定义:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.3有理数的乘法(1)
浙教版版七年级上册
教学目标
2.掌握有理数的乘法法则.
1.回顾小学所学数的乘法,经历乘法法则的发生过程.
3.会运用乘法法则求若干个有理数相乘的积.
4.理解倒数的概念.
复习回顾
正有理数
有理数
引入负数
运算
运算
2 × 3 = 6
2 × (3) =
(2 )× (3) =
(2 ) × 3 =
新知探究
如图,有一只蜗牛沿直线爬行,它现在位于点O.
0
0
2
4
6
8
每分钟2cm的速度向右记为 ;3分钟以后记为 .
其结果可表示为 .
+2cm/min
问题一:如果蜗牛一直以每分2cm的速度从O点向右爬行,3分钟后它
在点O的 边 cm处?
右
6
+3min
即 .
(+2)×(+3)= +6
( )+( )+( )= +6
+2 +2 +2
新知探究
其结果可表示为 .
0
8
6
4
2
(-2)×(+3)=-6
问题二:如果蜗牛一直以每分2cm的速度从O点向左爬行,
3分钟后它在点O的 边 cm处?
左
6
每分钟2cm的速度向左记为 ;3分钟以后记为 .
2cm/min
+3min
即 .
( )+( )+( )= -6
-2 -2 -2
新知探究
问题三:如果蜗牛一直以每分2cm的速度向右爬行,现在蜗牛在O点处,
那么3分钟前它在点O的 边 cm处?
0
8
6
4
2
左
6
每分钟2cm的速度向右记为 ;3分钟前记为 .
2cm/min
3min
其结果可表示为 .
(+2)×( 3 )=-6
新知探究
问题四:如果蜗牛一直以每分2cm的速度向左爬行,现在蜗牛在O点处,
那么3分钟前它在点O的 边 cm处?
0
右
6
2
4
6
8
每分钟2cm的速度向左记为 ;3分钟前记为 .
2cm/min
3min
其结果可表示为 .
(2)×( 3 )
6
=
归纳总结
(+2)×(+3)= +6
(+2)×(3)=6
(2)×(+3)=6
比较算式,探寻运算规律
改变一个数的符号,积就变为原来的相反数.
(2)×(+3)= (2×3)= 6
(+2)×(3)= (2×3)=6
( 2 )×(3 )= +6
(2)×(3)= (2×3)= 6
改变两个数的符号,积就变为原来的数.
新知讲解
同号得正
异号得负
绝
对
值
相
乘
(+2)×(+3) =
+6
(-2 )×(-3) =
(+2 )×(-3) =
(-2 )×(+3) =
+6
-6
-6
0×(+3)=
0×(3)=
0
0
任何数同零相乘,积为零.
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数同零相乘,积为零.
牛刀小试
1、不计算,直接确定下列积的符号:
(1) 35×(-13) (2)(-14)×6
(3)(-7)×(-19) (4) 1.5×2.7
-
+
-
+
2、用“<”,“>”或“=”填空
(1)( 7)×(+3) 0. (2)( 13)×( 7.9) 0.
(3)0× ( ) 0. (4)(1) ×() ×(1.5)_____0.
<
>
=
<
典例精析
例1 : 计算:
(1)
(2)( 2.5)×4
(3)( 5)×0×
(4)( )×( 3)
(5)( 6)×( )×( 4)
=1
= (2.5×4)
= 10
=0
=+(×3)
=1
= (6××4)
= 30
几个有理数相乘,怎样确定积的符号?
多个不为零的有理数相乘,积的符号由负因数的个数确定.
负因数的个数为奇数时,积为负;负因数的个数为偶数时,积为正.
新知讲授
( )×( 3)
若两个有理数的乘积为1,就称这两个有理数互为倒数.
例如, 是 的倒数, 也是 的倒数.
练习: 的倒数是______ ,
8的倒数是______ ,
1的倒数是______ , 0的倒数是
1
7
0没有倒数
因为任何数与0相乘,积为0,不存在与0相乘积为1的数.
什么数的倒数是它本身?
1和1
要点提炼
注意事项
(1)0没有倒数.
(2)求分数的倒数,只要把这个分数的分子,分母颠倒位置即可.
(3)正数的倒数是正数,负数的倒数是负数.
(4)求小数的倒数时,要先把小数化成分数.
(5)求带分数的倒数时,要先把带分数化成假分数.
试探寻下列数的倒数
1 0.2 3 1 1
倒数
7
0
不存在
1
1
5
课堂练习
1、下列各式中,积为负数的是 ( )
A. (-5)×(-2)×(-3)×(-7) B. (-5)×(-2)×|-3|
C. (-5)×2×0×(-7) D. (-5)×2×(-3)×(-7)
2、下列关系式正确的是 ( )
A. |-3|<0 B. -(-3)<0 C. -3+2>0 D. -3×2<0
3、若|x|=4,|y|=7,且xy<0,则x+y的值为 ( )
A. 11或-11 B. 3或-3 C. 11或3 D. -11或-3
4、两个有理数的和为正数,积为负数,则这两个有理数是 ( )
A. 两个正数 B. 两个负数
C. 一正一负且正数的绝对值较大 D. 一正一负且负数的绝对值较大
D
D
B
C
5、下列说法中,正确的是 ( )
A. 0的倒数是0 B. 倒数是它本身的数是1
C. 相反数等于它本身的数是负数 D. 绝对值最小的数是0
D
6、计算:
(1)
(3)
(2)
(4)( 2)×3×( 0.5)
(6)( )×( )×( 2)
(5)| 1.25|×( 8)×4
=
=
=
=3
=
= 40
7、把 6表示成两个整数的积,有多少种可能?把它们全部写出来.
1
8、在数5,1,,5,中任取三个数相乘,其中最大的积是a,最小的积是b,求a,b的值.
a=5(4) 5=100
b=5(4) () =
课堂总结
通过本节课的交流,你有什么体验或收获
1.两数相乘,同号得 ,异号得 ,再把绝对值相乘;
0 乘任何数得 .
正
负
0
2.几个有理数相乘,因数都不为 0 时,
积的符号由 确定.
负因数的个数
奇数个为负,偶数个为正
有一因数为 0 时,积是
0 .
3. 倒数的定义
若两个有理数的乘积为1,就称这两个有理数互为倒数.
作业布置
1.作业本
2.教材练习题
拓展提升
1、若|a|=3, |b|=5,则a×b=________________.
2、已知a,b 互为相反数, c,d 互为倒数, m 的绝对值为2,
求 (a+b)c×d+m的值.
15或15
∵ a,b 互为相反数, c,d 互为倒数, m 的绝对值为2
∴ a+b = 0 ,c×d = 1, m = 2
∴ (a+b)c×d+m= 0+1+m = 3或1
3、若定义一种新的运算“*”,规定有理数a*b=4ab,如2*3=4×2×3=24.
(1)求3*(4)的值; (2)求(2)*(6*3)的值.
(1)3*(4)=4×3×(4)=48;
(2)(2)*(6*3)=(2)*(4×6×3)=(2)*(72)=4×(2)×(72)=576.
解:
趣味数学
如图,A,B两点在数轴上对应的数分别为a,b,且点A在点B的左边,|a|=10,|b|=90,a×b<0.
(1)求a,b的值.
(2)现有一只电子蚂蚁P从点A出发,以3个单位长度/秒的速度向右运动,同时另一只电子蚂蚁Q从点B出发,以2个单位长度/秒的速度向左运动.
①设两只电子蚂蚁在数轴上的点C相遇,求出点C对应的数是多少.
②经过多长时间,两只电子蚂蚁在数轴上相距20个单位长度?
板书设计
2.3有理数的乘法(1)
1.乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数与零相乘,积为零.
2.多个不为零的有理数相乘,积的符号由负因数的个数确定.
负因数的个数为奇数时,积为负;负因数的个数为偶数时,积为正.
若两个有理数的乘积为1,就称这两个有理数互为倒数.
3.倒数的定义:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
