二次函数y=a(x-h)2的图象与性质(二)
文档属性
| 名称 | 二次函数y=a(x-h)2的图象与性质(二) |

|
|
| 格式 | zip | ||
| 文件大小 | 61.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-06 21:39:13 | ||
图片预览

文档简介
课 题:《二次函数y=a(x-h)2的图象与性质(二)》
序 号: ( 8 )
年 级: 九年级 单元名称:第27章二次函数
课 型: 新授课 上课时间:
学习内容: 华东师大版 11--13页
1 会画这类函数的图象,并掌握这类函数的性质.
2知道二次函数与的联系
重 点:知道二次函数与的联系
难 点:掌握抛物线平移至的规律
学法指导:合作探究
学 习 过 程
自主预习课本 11--13页,完成下列各题:
1把抛物线y=-x2向左平移_______个单位,就得到抛物线y=-(x+1)2 ;
2把抛物线y=-x2向右平移_______个单位,就得到抛物线y=-(x-1)2
3.如果要得到抛物线,应将抛物线向 平移 单位.
4.如果要得到抛物线,应将抛物线向 平移 单位.
函数 大致图象 开口方向 顶点坐标 对称轴 最值 增减性
当时,取最 值 . 在对称轴左侧随的增大而 ;在对称轴右侧随的增大而 .
当时,取最 值 . 在对称轴左侧随的增大而 ;在对称轴右侧随的增大而 .
当时,取最 值 . 在对称轴左侧随的增大而 ;在对称轴右侧随的增大而 .
1填空:
2抛物线向 平移 个单位可得抛物线.
3当时的图象,可以由函数的图象向 平移得到;当时的图象,可以由函数的图象向 平移得到。
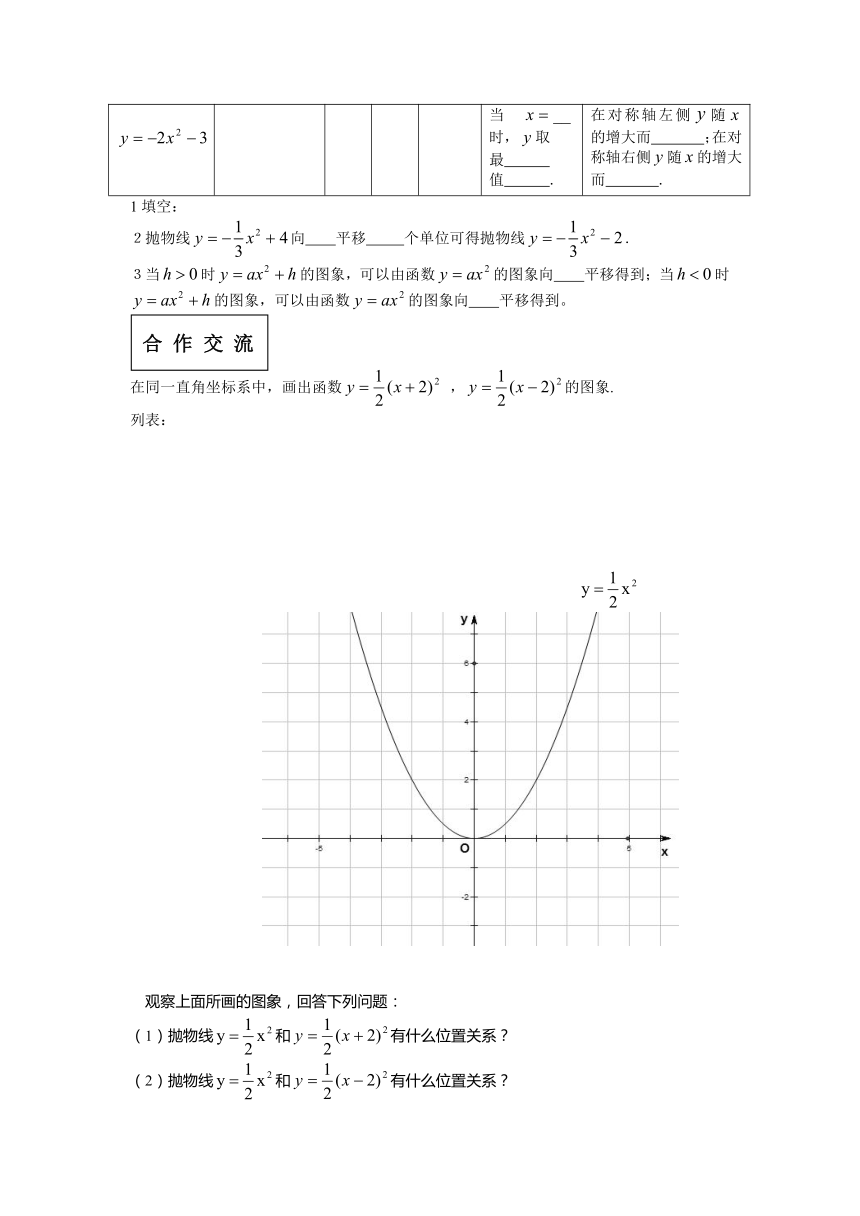
在同一直角坐标系中,画出函数 ,的图象.
列表:
观察上面所画的图象,回答下列问题:
抛物线和有什么位置关系?
抛物线和有什么位置关系?
抛物线和有什么位置关系?
(4)抛物线和有什么位置关系?
归纳:
注意:把抛物线作左右平移,是对x作加减,规律是:左加右减。
学以致用:
1.抛物线向右平移4个单位后,得到的抛物线的表达式为___________________;
抛物线向左平移3个单位后,得到的抛物线的表达式为___________________;
抛物线向右平移1个单位后,得到的抛物线解析式为_______________;
抛物线y=-(x-1)x2向左平移2个单位后,得到的抛物线解析式为_______________。
2.抛物线可以看作抛物线沿x轴向______平移____个单位得到。
3.抛物线是由抛物线__________________向右平移2个单位得到的;
抛物线是由抛物线__________________向左平移3个单位得到的
4.抛物线y=m (x+n)2向左平移2个单位后,得到的函数关系式是y=-4 (x-4)2,则
m=__________,n=___________.
跟踪练习:抛物线向右平移3个单位后得到抛物线,则
5.把抛物线向左平移3个单位,再向上平移2个单位,得到的抛物线的解析式为 ,此时抛物线的开口方向 ,顶点坐标为 ,对称轴为 .
跟踪练习:把抛物线向右平移4个单位,再向下平移3个单位,得到的抛物线的解析式为 ,此时抛物线的开口方向 ,顶点坐标为 ,对称轴为 .
将抛物线 y=ax2 向右平移后,所得新抛物线的顶点横坐标为3,且新抛物线经过点(2,4),求a的值。
7.将抛物线 y=-2x2 左右平移,使得它与x轴相交于点A,与y轴相交于点B。若△ABO的面积为27,求平移后的抛物线的解析式。
1将抛物向左平移1个单位后,得到的抛物线的解析式是 .
把抛物线y=3x2向右平移4个单位后,得到的抛物线的表达式为____________________.
2的图象是由 向右平移4个单位得到.
3若将抛物线y=2x2+1向下平移2个单位后,得到的抛物线解析式为_______________.
4将抛物线沿轴向下平移2个单位得到的抛物线的解析式为 ,再沿轴向上平移3个单位得到的抛物线的解析式为 .
5将二次函数的图象沿轴向上平移3个单位长度得到的函数解析式为 ,再沿轴向左平移7个单位长度得到的函数解析式为 .
6 把抛物线沿轴向下平移7个单位得到的抛物线的解析式为,
则a= ,c= .
7把抛物线沿轴向右平移3个单位长度得到的新的二次函数解析式为,则 , .
8将抛物线向左平移后所得新抛物线的顶点横坐标为 -2,且新抛物线经过点
(1,3),求的值.
预 习 检 测
知 识 准 备
合 作 交 流
课 后 反 思
达 标 检 测
课 后 反 思
序 号: ( 8 )
年 级: 九年级 单元名称:第27章二次函数
课 型: 新授课 上课时间:
学习内容: 华东师大版 11--13页
1 会画这类函数的图象,并掌握这类函数的性质.
2知道二次函数与的联系
重 点:知道二次函数与的联系
难 点:掌握抛物线平移至的规律
学法指导:合作探究
学 习 过 程
自主预习课本 11--13页,完成下列各题:
1把抛物线y=-x2向左平移_______个单位,就得到抛物线y=-(x+1)2 ;
2把抛物线y=-x2向右平移_______个单位,就得到抛物线y=-(x-1)2
3.如果要得到抛物线,应将抛物线向 平移 单位.
4.如果要得到抛物线,应将抛物线向 平移 单位.
函数 大致图象 开口方向 顶点坐标 对称轴 最值 增减性
当时,取最 值 . 在对称轴左侧随的增大而 ;在对称轴右侧随的增大而 .
当时,取最 值 . 在对称轴左侧随的增大而 ;在对称轴右侧随的增大而 .
当时,取最 值 . 在对称轴左侧随的增大而 ;在对称轴右侧随的增大而 .
1填空:
2抛物线向 平移 个单位可得抛物线.
3当时的图象,可以由函数的图象向 平移得到;当时的图象,可以由函数的图象向 平移得到。
在同一直角坐标系中,画出函数 ,的图象.
列表:
观察上面所画的图象,回答下列问题:
抛物线和有什么位置关系?
抛物线和有什么位置关系?
抛物线和有什么位置关系?
(4)抛物线和有什么位置关系?
归纳:
注意:把抛物线作左右平移,是对x作加减,规律是:左加右减。
学以致用:
1.抛物线向右平移4个单位后,得到的抛物线的表达式为___________________;
抛物线向左平移3个单位后,得到的抛物线的表达式为___________________;
抛物线向右平移1个单位后,得到的抛物线解析式为_______________;
抛物线y=-(x-1)x2向左平移2个单位后,得到的抛物线解析式为_______________。
2.抛物线可以看作抛物线沿x轴向______平移____个单位得到。
3.抛物线是由抛物线__________________向右平移2个单位得到的;
抛物线是由抛物线__________________向左平移3个单位得到的
4.抛物线y=m (x+n)2向左平移2个单位后,得到的函数关系式是y=-4 (x-4)2,则
m=__________,n=___________.
跟踪练习:抛物线向右平移3个单位后得到抛物线,则
5.把抛物线向左平移3个单位,再向上平移2个单位,得到的抛物线的解析式为 ,此时抛物线的开口方向 ,顶点坐标为 ,对称轴为 .
跟踪练习:把抛物线向右平移4个单位,再向下平移3个单位,得到的抛物线的解析式为 ,此时抛物线的开口方向 ,顶点坐标为 ,对称轴为 .
将抛物线 y=ax2 向右平移后,所得新抛物线的顶点横坐标为3,且新抛物线经过点(2,4),求a的值。
7.将抛物线 y=-2x2 左右平移,使得它与x轴相交于点A,与y轴相交于点B。若△ABO的面积为27,求平移后的抛物线的解析式。
1将抛物向左平移1个单位后,得到的抛物线的解析式是 .
把抛物线y=3x2向右平移4个单位后,得到的抛物线的表达式为____________________.
2的图象是由 向右平移4个单位得到.
3若将抛物线y=2x2+1向下平移2个单位后,得到的抛物线解析式为_______________.
4将抛物线沿轴向下平移2个单位得到的抛物线的解析式为 ,再沿轴向上平移3个单位得到的抛物线的解析式为 .
5将二次函数的图象沿轴向上平移3个单位长度得到的函数解析式为 ,再沿轴向左平移7个单位长度得到的函数解析式为 .
6 把抛物线沿轴向下平移7个单位得到的抛物线的解析式为,
则a= ,c= .
7把抛物线沿轴向右平移3个单位长度得到的新的二次函数解析式为,则 , .
8将抛物线向左平移后所得新抛物线的顶点横坐标为 -2,且新抛物线经过点
(1,3),求的值.
预 习 检 测
知 识 准 备
合 作 交 流
课 后 反 思
达 标 检 测
课 后 反 思
