二次函数y=a(x-h)2+k的图象与性质
文档属性
| 名称 | 二次函数y=a(x-h)2+k的图象与性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 64.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-06 21:39:46 | ||
图片预览

文档简介
课 题:《二次函数y=a(x-h)2+k的图象与性质(一)》
序 号: ( 9 )
年 级: 九年级 单元名称:第27章二次函数
课 型: 新授课 上课时间:
学习内容: 华东师大版 13---15页
学习目标:1.会画二次函数y=a (x-h)2+k的图象;
2.掌握二次函数y=a (x-h)2+k的性质;
3.会应用二次函数y=a (x-h)2+k的性质解题.
重 点:会应用二次函数y=a (x-h)2+k的性质解题.
难 点:会画二次函数y=a (x-h)2+k的图象
学法指导:合作探究
学 习 过 程
自主预习课本13---15页,完成下列各题:
1.抛物线的顶点坐标为 。
2.抛物线y=-3 (x+4)2+1中,当x=______时,y有最______值是________.
3..抛物线开口 ,顶点坐标是 ,对称轴是 ,当
x= 时,y有最 值为 。
4.函数,当x 时,y随x的增大而增大,当 时,y随x的增大而减小;当x 时,函数取最 值,值为 。
1目前我们已经学习了几种形式的二次函数?
2在同一坐标系中画出二次函数y=-x2 、 y=-x2-2、y=-(x+3)2的草图。
分别说出它们的性质。
说出抛物线y=-x2与y=-x2-2、 y=-(x+3)2的关系。
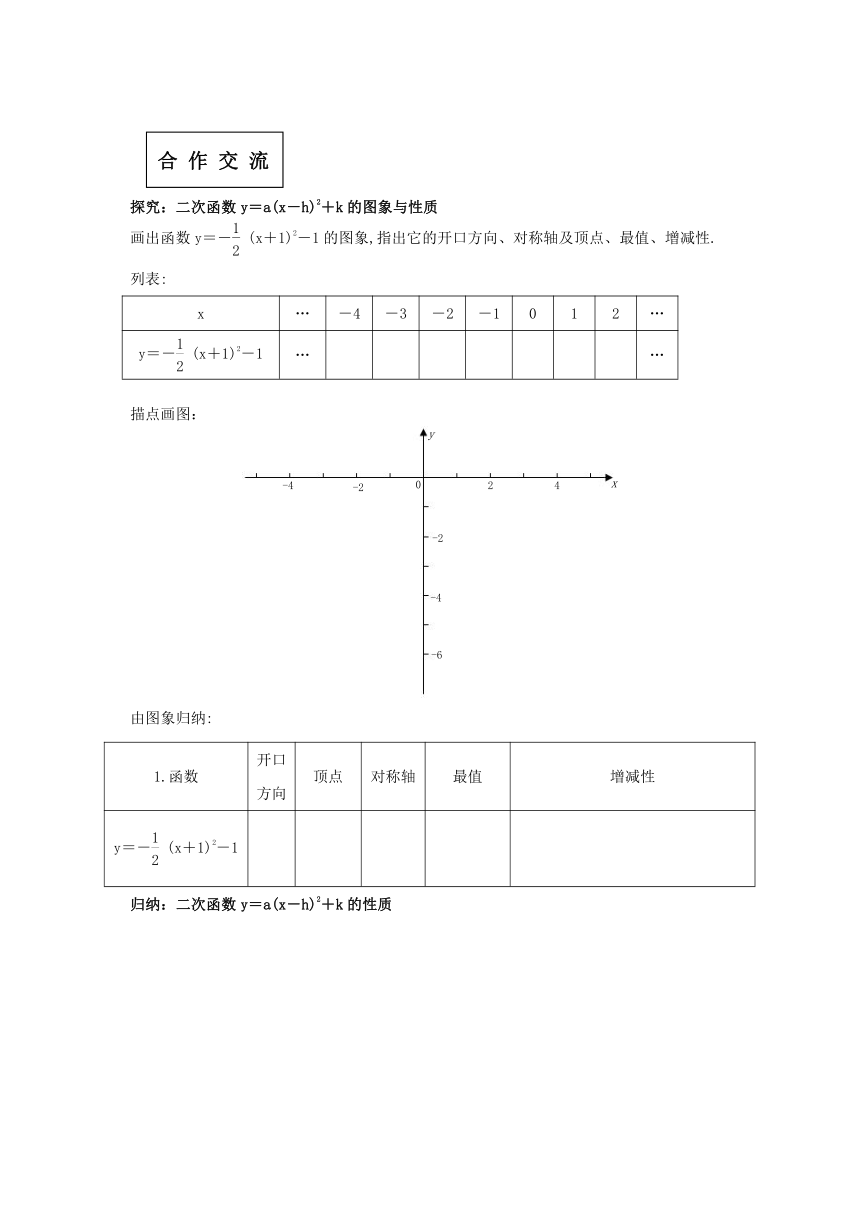
探究:二次函数y=a(x-h)2+k的图象与性质
画出函数y=-(x+1)2-1的图象,指出它的开口方向、对称轴及顶点、最值、增减性.
列表:
x … -4 -3 -2 -1 0 1 2 …
y=-(x+1)2-1 … …
描点画图:
由图象归纳:
1.函数 开口方向 顶点 对称轴 最值 增减性
y=-(x+1)2-1
归纳:二次函数y=a(x-h)2+k的性质
知识梳理:
y=ax2 y=ax2+k y=a (x-h)2 y=a (x-h)2+k
开口方向
顶点
对称轴
最值
增减性(对称轴右侧)
学以致用:1
y=3x2 y=-x2+1 y=(x+2)2 y=-4 (x-5)2-3
开口方向
顶点
对称轴
最值
增减性(对称轴左侧)
2顶点坐标为(-2,3),开口方向和大小与抛物线y=x2相同的解析式为( )
A.y=(x-2)2+3 B.y=(x+2)2-3 C.y=(x+2)2+3 D.y=-(x+2)2+3
3.已知二次函数的图象上有三个点,则的大小关系为( )
A、 B、 C、 D、
4.请选择一组你喜欢的a、h、k的值,使二次函数()的图象同时满足下列条件:①开口向下;②当x<2时,y随x的增大而增大;当x>2时,y随x的增大而减小。这样的二次函数的关系式可以是_________________。
抛物线y=4x2-1的开口 ,对称轴 ,顶点
坐标 ; 当x 时,取最 值;当
x 时,随的增大而增大,当x 时,随
的增大而减小. 其图象可以由 向 平移 得到.
2.抛物线y=(x-0.5)2的开口 ,对称轴 ,顶点
坐标 ; 当x 时,取最 值;当
x 时,随的增大而增大,当x 时,随
的增大而减小. 其图象可以由 向 平移 得到.
抛物线y=-6(x+2)2+5的开口 ,对称轴 ,
顶点坐标 ; 当时取最 值;当时
随的增大而增大,当时随的增大而减小.
4.函数的开口向 ,对称轴 ,顶点坐标
,当x= 时,y有最 值,此时y= ;当X 时,
y随x的增大而增大,当 时,y随x的增大而减小.
已知二次函数的图象上有三个点,
则的大小关系为( )
A、 B、 C、 D、
6.顶点坐标为(3,-5),开口方向和大小与抛物线y=-3x2相同的解析式为( )
A.y=3(x+3)2-5 B.y=-3(x+3)2+5 C .y=3(x-3)2-5 D.y=-3(x-3)2-5
预 习 检 测
知 识 准 备
合 作 交 流
达 标 检 测
课 后 反 思
序 号: ( 9 )
年 级: 九年级 单元名称:第27章二次函数
课 型: 新授课 上课时间:
学习内容: 华东师大版 13---15页
学习目标:1.会画二次函数y=a (x-h)2+k的图象;
2.掌握二次函数y=a (x-h)2+k的性质;
3.会应用二次函数y=a (x-h)2+k的性质解题.
重 点:会应用二次函数y=a (x-h)2+k的性质解题.
难 点:会画二次函数y=a (x-h)2+k的图象
学法指导:合作探究
学 习 过 程
自主预习课本13---15页,完成下列各题:
1.抛物线的顶点坐标为 。
2.抛物线y=-3 (x+4)2+1中,当x=______时,y有最______值是________.
3..抛物线开口 ,顶点坐标是 ,对称轴是 ,当
x= 时,y有最 值为 。
4.函数,当x 时,y随x的增大而增大,当 时,y随x的增大而减小;当x 时,函数取最 值,值为 。
1目前我们已经学习了几种形式的二次函数?
2在同一坐标系中画出二次函数y=-x2 、 y=-x2-2、y=-(x+3)2的草图。
分别说出它们的性质。
说出抛物线y=-x2与y=-x2-2、 y=-(x+3)2的关系。
探究:二次函数y=a(x-h)2+k的图象与性质
画出函数y=-(x+1)2-1的图象,指出它的开口方向、对称轴及顶点、最值、增减性.
列表:
x … -4 -3 -2 -1 0 1 2 …
y=-(x+1)2-1 … …
描点画图:
由图象归纳:
1.函数 开口方向 顶点 对称轴 最值 增减性
y=-(x+1)2-1
归纳:二次函数y=a(x-h)2+k的性质
知识梳理:
y=ax2 y=ax2+k y=a (x-h)2 y=a (x-h)2+k
开口方向
顶点
对称轴
最值
增减性(对称轴右侧)
学以致用:1
y=3x2 y=-x2+1 y=(x+2)2 y=-4 (x-5)2-3
开口方向
顶点
对称轴
最值
增减性(对称轴左侧)
2顶点坐标为(-2,3),开口方向和大小与抛物线y=x2相同的解析式为( )
A.y=(x-2)2+3 B.y=(x+2)2-3 C.y=(x+2)2+3 D.y=-(x+2)2+3
3.已知二次函数的图象上有三个点,则的大小关系为( )
A、 B、 C、 D、
4.请选择一组你喜欢的a、h、k的值,使二次函数()的图象同时满足下列条件:①开口向下;②当x<2时,y随x的增大而增大;当x>2时,y随x的增大而减小。这样的二次函数的关系式可以是_________________。
抛物线y=4x2-1的开口 ,对称轴 ,顶点
坐标 ; 当x 时,取最 值;当
x 时,随的增大而增大,当x 时,随
的增大而减小. 其图象可以由 向 平移 得到.
2.抛物线y=(x-0.5)2的开口 ,对称轴 ,顶点
坐标 ; 当x 时,取最 值;当
x 时,随的增大而增大,当x 时,随
的增大而减小. 其图象可以由 向 平移 得到.
抛物线y=-6(x+2)2+5的开口 ,对称轴 ,
顶点坐标 ; 当时取最 值;当时
随的增大而增大,当时随的增大而减小.
4.函数的开口向 ,对称轴 ,顶点坐标
,当x= 时,y有最 值,此时y= ;当X 时,
y随x的增大而增大,当 时,y随x的增大而减小.
已知二次函数的图象上有三个点,
则的大小关系为( )
A、 B、 C、 D、
6.顶点坐标为(3,-5),开口方向和大小与抛物线y=-3x2相同的解析式为( )
A.y=3(x+3)2-5 B.y=-3(x+3)2+5 C .y=3(x-3)2-5 D.y=-3(x-3)2-5
预 习 检 测
知 识 准 备
合 作 交 流
达 标 检 测
课 后 反 思
