浙教版九年级上册2.2.2简单事件的概率课件(共18张PPT)
文档属性
| 名称 | 浙教版九年级上册2.2.2简单事件的概率课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
浙教版数学九年级上册第二单元第二节第二课时
问题引入,回顾概念
问题:
(1)一个口袋内装有大小相等的1个白球和3个黑球,从中任意摸出1个球,摸出黑球的概率为______;
(2)有10张卡片(从1号到10号),从中任取1张,取到的卡号是3的倍数的概率为_______.
请先按暂停键!思考完成后
再按回播放键!
问题引入,回顾概念
在数学中,我们把事件发生的可能性的大小,称为事件发生的概率.
关键 ① 求事件所有可能的结果总数n
② 求事件A发生的可能的结果m (m ≤n)
公式
前提 所有结果发生的可能性相等,且互相排斥
深入探究,应用概念
例1 一个盒子里装有4个只有颜色不同的球,其中3个红球,1个白球.从盒子里摸出一个球,记下颜色后放回,并搅匀,再摸出一个球.
(1)写出两次摸球的所有可能的结果;
解:所有可能的结果所总数为n=4×4=16.
第1次
第2次
白
红1
红2
红3
白
红1
红2
红3
白,白
白,红1
白,红2
白,红3
红1,白
红1 ,红1
红1,红2
红1,红3
红2 ,白
红2,红1
红2 ,红2
红2 ,红3
红3 ,白
红3 ,红1
红3 ,红2
红3,红3
列表法
深入探究,应用概念
第1次
第2次
白
红1
红2
红3
白
红1
红2
红3
白,白
白,红1
白,红2
白,红3
红1,白
红1 ,红1
红1,红2
红1,红3
红2 ,白
红2,红1
红2 ,红2
红2 ,红3
红3 ,白
红3 ,红1
红3 ,红2
红3,红3
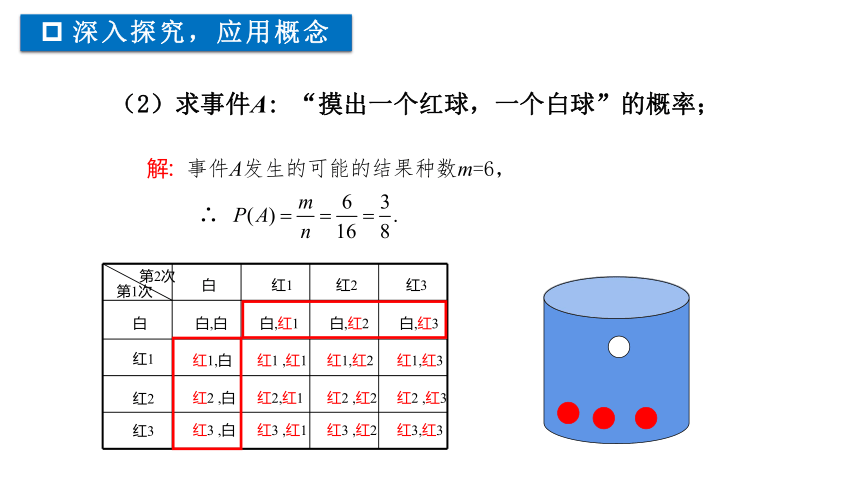
解: 事件A发生的可能的结果种数m=6,
∴
(2)求事件A: “摸出一个红球,一个白球”的概率;
深入探究,应用概念
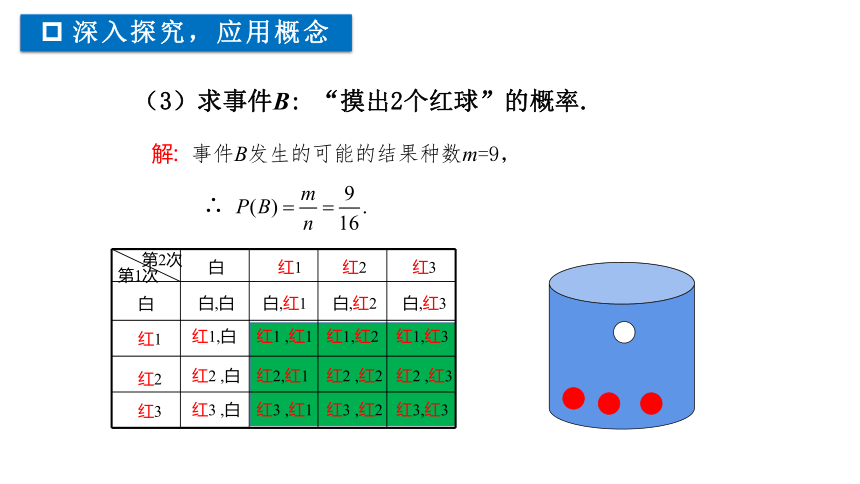
(3)求事件B: “摸出2个红球”的概率.
解: 事件B发生的可能的结果种数m=9,
∴
第1次
第2次
白
红1
红2
红3
白
红1
红2
红3
白,白
白,红1
白,红2
白,红3
红1,白
红1 ,红1
红1,红2
红1,红3
红2 ,白
红2,红1
红2 ,红2
红2 ,红3
红3 ,白
红3 ,红1
红3 ,红2
红3,红3
深入探究,应用概念
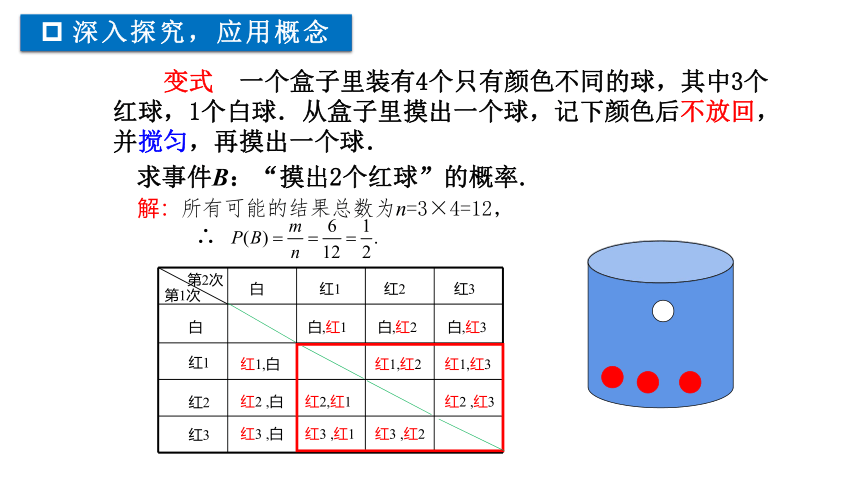
变式 一个盒子里装有4个只有颜色不同的球,其中3个红球,1个白球.从盒子里摸出一个球,记下颜色后不放回,并搅匀,再摸出一个球.
求事件B:“摸出2个红球”的概率.
第1次
第2次
白
红1
红2
红3
白
红1
红2
红3
白,红1
白,红2
白,红3
红1,白
红1,红2
红1,红3
红2 ,白
红2,红1
红2 ,红3
红3 ,白
红3 ,红1
红3 ,红2
解:所有可能的结果总数为n=3×4=12,
∴
深入探究,应用概念
例2 学校组织春游,安排给九年级3辆车,小明与小慧都可以从这3辆车中任选一辆搭乘.问小明与小慧同车的概率有多大
甲
乙
丙
甲
乙
丙
甲
乙
丙
小明
选的车
甲
乙
丙
小慧
选的车
树状图
∴所有可能的结果总数为n=9,
小明与小慧同车的结果总数为m=3,
答:小明与小慧同车的概率是 .
解:记这三辆车分别为甲、乙、丙,
解:记这三辆车分别为甲、乙、丙,小明与小慧乘车的所有可能的
结果列表如下:(各种结果发生的可能性相同)
小慧选的车
小明选的车 甲 乙 丙
甲 甲,甲 甲,乙 甲,丙
乙 乙,甲 乙,乙 乙,丙
丙 丙,甲 丙,乙 丙,丙
小慧选的车
小明选的车 甲 乙 丙
甲 甲,甲 甲,乙 甲,丙
乙 乙,甲 乙,乙 乙,丙
丙 丙,甲 丙,乙 丙,丙
深入探究,应用概念
列表法
答:小明与小慧同车的概率是 .
练习1 小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问小明正好穿的是相同的一双袜子的概率是多少?
解:设两双袜子分别为A1、A2、B1、B2,则
A1 A2 B 1 B2
开始
A2 B1 B2 A1 B1 B2 A1 A2 B2 A1 A2 B1
答:穿相同一双袜子的概率为
√
√
√
√
习题演练,掌握新知
练习2 在一个口袋中有4个完全相同的小球,把它们分别标上数字-1,0,1,2,随机摸出一个小球记录数字然后放回,在随机的摸出一个小球记录数字.求下列事件的概率:
(1)两次都是正数的概率P(A); (2)两次的数字和等于0的概率P(B).
深入探究,应用概念
解:根据题意,可以用以下表格表示所有不同的结果.
第一次
第二次 -1 0 1 2
-1 (-1,-1) (0,-1) (1,-1) (2,-1)
0 (-1,0) (0,0) (1,0) (2,0)
1 (-1,1) (0,1) (1,1) (2,1)
2 (-1,2) (0,2) (1,2) (2,-2)
深入探究,应用概念
深化拓展,体悟新知
例3 如图,转盘的白色扇形和红色扇形的圆心角分别为120°和240°.让转盘自由转动2次,求指针一次落在白色区域,另一次落在红色区域的概率.
问题 发生的可能性不相等
策略 不等变相等
白色
红Ⅰ
红Ⅱ
白色
红Ⅰ
红Ⅱ
白色
白色
红Ⅰ
红Ⅰ
红Ⅱ
红Ⅱ
深化拓展,体悟新知
解:把红色扇形划分成两个圆心角都是120°的扇形(如图)
Ⅰ
Ⅱ
所有可能的结果总数为n=3×3=9,指针一次 落在白色区域,另一次落在红色区域的结果总数为m=4.
深化拓展,体悟新知
练习 如图,转盘的黄色扇形和绿色扇形的圆心角分别为90°和270°.让转盘自由转动2次,求指针2次都落在绿色区域的概率.
拓展 有甲、乙转盘如图,分别将甲、乙转盘各自由转动1次,求指针分别落在红色和绿色区域的概率.
深化拓展,体悟新知
甲
乙
白
红 Ⅰ
红 Ⅱ
绿 Ⅲ
黄
绿 Ⅰ
绿 Ⅱ
甲
乙
绿 Ⅲ
黄
绿 Ⅰ
绿 Ⅱ
绿 Ⅲ
黄
绿 Ⅰ
绿 Ⅱ
小结新课,梳理新知
简单事件的概率
直接求
二重条件
多重条件
一重条件
树状图或列表法
树状图
所有结果发生的可能性相等
类型
策略
公式
策略 不等变相等
所有结果发生的可能性不相等
同学们再见
浙教版数学九年级上册第二单元第二节第二课时
问题引入,回顾概念
问题:
(1)一个口袋内装有大小相等的1个白球和3个黑球,从中任意摸出1个球,摸出黑球的概率为______;
(2)有10张卡片(从1号到10号),从中任取1张,取到的卡号是3的倍数的概率为_______.
请先按暂停键!思考完成后
再按回播放键!
问题引入,回顾概念
在数学中,我们把事件发生的可能性的大小,称为事件发生的概率.
关键 ① 求事件所有可能的结果总数n
② 求事件A发生的可能的结果m (m ≤n)
公式
前提 所有结果发生的可能性相等,且互相排斥
深入探究,应用概念
例1 一个盒子里装有4个只有颜色不同的球,其中3个红球,1个白球.从盒子里摸出一个球,记下颜色后放回,并搅匀,再摸出一个球.
(1)写出两次摸球的所有可能的结果;
解:所有可能的结果所总数为n=4×4=16.
第1次
第2次
白
红1
红2
红3
白
红1
红2
红3
白,白
白,红1
白,红2
白,红3
红1,白
红1 ,红1
红1,红2
红1,红3
红2 ,白
红2,红1
红2 ,红2
红2 ,红3
红3 ,白
红3 ,红1
红3 ,红2
红3,红3
列表法
深入探究,应用概念
第1次
第2次
白
红1
红2
红3
白
红1
红2
红3
白,白
白,红1
白,红2
白,红3
红1,白
红1 ,红1
红1,红2
红1,红3
红2 ,白
红2,红1
红2 ,红2
红2 ,红3
红3 ,白
红3 ,红1
红3 ,红2
红3,红3
解: 事件A发生的可能的结果种数m=6,
∴
(2)求事件A: “摸出一个红球,一个白球”的概率;
深入探究,应用概念
(3)求事件B: “摸出2个红球”的概率.
解: 事件B发生的可能的结果种数m=9,
∴
第1次
第2次
白
红1
红2
红3
白
红1
红2
红3
白,白
白,红1
白,红2
白,红3
红1,白
红1 ,红1
红1,红2
红1,红3
红2 ,白
红2,红1
红2 ,红2
红2 ,红3
红3 ,白
红3 ,红1
红3 ,红2
红3,红3
深入探究,应用概念
变式 一个盒子里装有4个只有颜色不同的球,其中3个红球,1个白球.从盒子里摸出一个球,记下颜色后不放回,并搅匀,再摸出一个球.
求事件B:“摸出2个红球”的概率.
第1次
第2次
白
红1
红2
红3
白
红1
红2
红3
白,红1
白,红2
白,红3
红1,白
红1,红2
红1,红3
红2 ,白
红2,红1
红2 ,红3
红3 ,白
红3 ,红1
红3 ,红2
解:所有可能的结果总数为n=3×4=12,
∴
深入探究,应用概念
例2 学校组织春游,安排给九年级3辆车,小明与小慧都可以从这3辆车中任选一辆搭乘.问小明与小慧同车的概率有多大
甲
乙
丙
甲
乙
丙
甲
乙
丙
小明
选的车
甲
乙
丙
小慧
选的车
树状图
∴所有可能的结果总数为n=9,
小明与小慧同车的结果总数为m=3,
答:小明与小慧同车的概率是 .
解:记这三辆车分别为甲、乙、丙,
解:记这三辆车分别为甲、乙、丙,小明与小慧乘车的所有可能的
结果列表如下:(各种结果发生的可能性相同)
小慧选的车
小明选的车 甲 乙 丙
甲 甲,甲 甲,乙 甲,丙
乙 乙,甲 乙,乙 乙,丙
丙 丙,甲 丙,乙 丙,丙
小慧选的车
小明选的车 甲 乙 丙
甲 甲,甲 甲,乙 甲,丙
乙 乙,甲 乙,乙 乙,丙
丙 丙,甲 丙,乙 丙,丙
深入探究,应用概念
列表法
答:小明与小慧同车的概率是 .
练习1 小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问小明正好穿的是相同的一双袜子的概率是多少?
解:设两双袜子分别为A1、A2、B1、B2,则
A1 A2 B 1 B2
开始
A2 B1 B2 A1 B1 B2 A1 A2 B2 A1 A2 B1
答:穿相同一双袜子的概率为
√
√
√
√
习题演练,掌握新知
练习2 在一个口袋中有4个完全相同的小球,把它们分别标上数字-1,0,1,2,随机摸出一个小球记录数字然后放回,在随机的摸出一个小球记录数字.求下列事件的概率:
(1)两次都是正数的概率P(A); (2)两次的数字和等于0的概率P(B).
深入探究,应用概念
解:根据题意,可以用以下表格表示所有不同的结果.
第一次
第二次 -1 0 1 2
-1 (-1,-1) (0,-1) (1,-1) (2,-1)
0 (-1,0) (0,0) (1,0) (2,0)
1 (-1,1) (0,1) (1,1) (2,1)
2 (-1,2) (0,2) (1,2) (2,-2)
深入探究,应用概念
深化拓展,体悟新知
例3 如图,转盘的白色扇形和红色扇形的圆心角分别为120°和240°.让转盘自由转动2次,求指针一次落在白色区域,另一次落在红色区域的概率.
问题 发生的可能性不相等
策略 不等变相等
白色
红Ⅰ
红Ⅱ
白色
红Ⅰ
红Ⅱ
白色
白色
红Ⅰ
红Ⅰ
红Ⅱ
红Ⅱ
深化拓展,体悟新知
解:把红色扇形划分成两个圆心角都是120°的扇形(如图)
Ⅰ
Ⅱ
所有可能的结果总数为n=3×3=9,指针一次 落在白色区域,另一次落在红色区域的结果总数为m=4.
深化拓展,体悟新知
练习 如图,转盘的黄色扇形和绿色扇形的圆心角分别为90°和270°.让转盘自由转动2次,求指针2次都落在绿色区域的概率.
拓展 有甲、乙转盘如图,分别将甲、乙转盘各自由转动1次,求指针分别落在红色和绿色区域的概率.
深化拓展,体悟新知
甲
乙
白
红 Ⅰ
红 Ⅱ
绿 Ⅲ
黄
绿 Ⅰ
绿 Ⅱ
甲
乙
绿 Ⅲ
黄
绿 Ⅰ
绿 Ⅱ
绿 Ⅲ
黄
绿 Ⅰ
绿 Ⅱ
小结新课,梳理新知
简单事件的概率
直接求
二重条件
多重条件
一重条件
树状图或列表法
树状图
所有结果发生的可能性相等
类型
策略
公式
策略 不等变相等
所有结果发生的可能性不相等
同学们再见
同课章节目录
