2022-2023学年浙教版八年级数学上册1.2定义与命题提升练习(word版含答案)
文档属性
| 名称 | 2022-2023学年浙教版八年级数学上册1.2定义与命题提升练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 181.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-08 20:25:07 | ||
图片预览




文档简介
浙教版-8年级-上册-数学-第1章《三角形的初步知识》
1.2 定义与命题(1)定义与命题
【知识点-部分】
1、定义:用来说明一个名词或术语的意义的语句。
形式: ……叫做(是、为)……;
注:定义是严密的,避免使用含糊不清的术语。
2、命题:判断一件事情的句子,每个命题都由条件和结论两部分组成。
形式:如果(若)…那么(则)…
含义:(1)命题必须是一个完整的句子;(2)这个句子必须对某件事情作出肯定或否定的判断。
注:有些命题的条件和结论不够明显,要把命题改写成“如果……那么……”的形式,再找条件和结论。
1.2 定义与命题(2)真假命题、基本事实与定理
【知识点-部分】
一、真假命题、反证法
1、真命题:正确的命题(真命题在条件成立时,结论无一例外地成立)。
2、假命题:不正确的命题(假命题在条件成立时,结论却不能保证总是成立)。
3、反例:举一个例子,若具有命题的条件,而不具有命题的结论,这种例子称为反例。
注:(1)说明一个命题是真命题,需要根据定义、公理、定理进行严格证明才行;
(2)说明一个命题是假命题,举出一个反例即可。
4、证明的必要性:
(1)证明的定义:要判断一个命题是不是真命题,仅仅依靠经验、观察、实验和猜想是不够的,必须一步步、有根有据的进行推理。推理的过程叫做证明
(2)步骤:1) 理解题意:分清命题的条件(已知),结论(求证) 2)根据题意,画出图形;
3)结合图形,用符号语言写出“已知”和“求证 4)分析题意,探索证明思路; 5)写出证明过程;
方法:举出反例、推理证明、反证法
5、反证法:假设命题不成立,从这样的假设出发,经过推理得出和已知条件矛盾,或者与定义,公理,定理等矛
盾,从而得出假设命题不成立是错误的,即所求证的命题正确.
步骤:(1)反设(否定结论);(2)归谬(利用已知条件和反设,已学过的公理、定理、定义、法则,
进行推理,得出与已学过的公理、定理、或与已知条件,或与假设矛盾);
(3)写出结论(肯定原命题成立)。
二、公理与定理
一、公理-1、公理定义:通过长期实践总结出来,并且被人们公认的真命题叫做公理。
注:(1)公里是不需要推理证明的真命题; (2)公理可作为判断其他命题真假的依据。
2、常见公理:(1)同位角相等,两直线平行; (2)两直线平行,同位角相等;
(3)两边及其夹角对应相等的两个三角形全等; (4)两角及其夹边对应相等的两个三角形全等;
(5)三边对应相等的两个三角形全等; (6)全等三角形的对应边相等,对应角相等;
(7)两点确定一条直线; (8)等式的有关性质和不等式的有关性质都可以看做公理;
例如:“在等式或不等式中,一个量可以用它的等量来代替”简称为“等量代换”。
二、定理-1、定理:通过推理得到证实的真命题叫做定理。
注:(1)定理都是真命题,但真命题不一定都是定理; (2)定理可作为判断其他命题真假的依据。
【典型例题-精选部分】
1、下面是六个推断:
① 因为平角的两条边在一条直线上,所以直线是一个平角.
② 因为周角的两条边在一条射线上,所以射线是一个周角.
③ 因为扇形是圆的一部分,所以圆周的一部分是扇形.
④ 因为平行的线段没有交点,所以不相交的两条线段平行.
⑤ 因为正方形的边长都相等,所以边长相等的四边形是正方形.
⑥ 因为等腰三角形有两个内角相等,所以有两个内角相等的三角形是等腰三角形.
其中正确的结论有 个,其序号是 .
2、数学上往往是先有猜想,猜想被证明正确后便成为定理.黎曼猜想(也称黎曼假设)是100多年前由德国著名数学家黎曼提出的,它是世界上最重要的数学猜想之一.有大约1000个数学命题,一旦黎曼猜想得到证明,它们就必然成立.黎曼猜想与物理学、密码学也有深刻的联系.黎曼猜想与以下数学式有关:1+++…++…
当s=1时,上式就是所有正整数的倒数的和1+++…++…(*)
随着n的无限增加,(*)式中的第n项将无限接近于0,那么(*)式的值会比10大吗?会比10000大吗?
自然的感觉是“聚沙成塔”、“积少成多”,即设法把很多小小的项累加起来变大,下面是实现这个想法的一种组合法:1++(+)+(+++)+(+++++++)+…+
>1++(+)+(+++)+(+++++++)+…+
用这种方法可以判定(*)式中:
(1)从第一项1开始,一共 项的和就可以大于3;
(2)从第一项1开始,一共 项的和就可以大于6.
3、判断下列命题是真命题还是假命题;如果是假命题,请举一个反例
(1)两个锐角的和是锐角;
(2)若a>b,则a2>b2;
(3)若n是自然数,则代数式(3n+1)(3n+2)+1的值是3的倍数.
4、请判断下列命题的真假性,若是假命题请举反例说明.
(1)若a>b,则a2>b2;
(2)两个无理数的和仍是无理数;
(3)若三角形三边a,b,c满足(a﹣b)(b﹣c)(c﹣a)=0,则三角形是等边三角形;
(4)若三条线段a,b,c满足a+b>c,则这三条线段a,b,c能够组成三角形.
5、把下列命题改写成“如果…那么…”的形式.
(1)两直线平行,同位角相等;
(2)在同一个三角形中,等角对等边;
(3)同角的补角相等;
(4)两个无理数的积仍是无理数.
6、将下列命题改写成“如果…,那么…”的形式.
(1)能被2整除的数也能被4整除;
(2)相等的两个角是对顶角;
(3)若xy=0,则x=0;
(4)角平分线上的点到这个角两边的距离相等.
7、下列定理中,哪些有逆定理?如果有逆定理,写出它的逆定理.
(1)全等三角形的对应角相等.
(2)同旁内角互补,两直线平行.
8、请写出下列命题的逆命题,并判断这些逆命题是否成立.
(1)同旁内角相等,两直线平行.
(2)如果两个角是直角,那么这两个角相等.
9、对几何命题进行逆向思考是几何研究中的重要策略,我们知道,等腰三角形两腰上的高 线相等,那么等腰三角形两腰上的中线,两底角的角平分线也分别相等吗?它们的逆命 题会正确吗?
(1)请判断下列命题的真假,并在相应命题后面的括号内填上“真”或“假”.
① 等腰三角形两腰上的中线相等
② 等腰三角形两底角的角平分线相等
③ 有两条角平分线相等的三角形是等腰三角形
(2)请写出“等腰三角形两腰上的中线相等”的逆命题,如果逆命题为真,请画出图形,写出已知、求证并进行证明,如果不是,请举出反例.
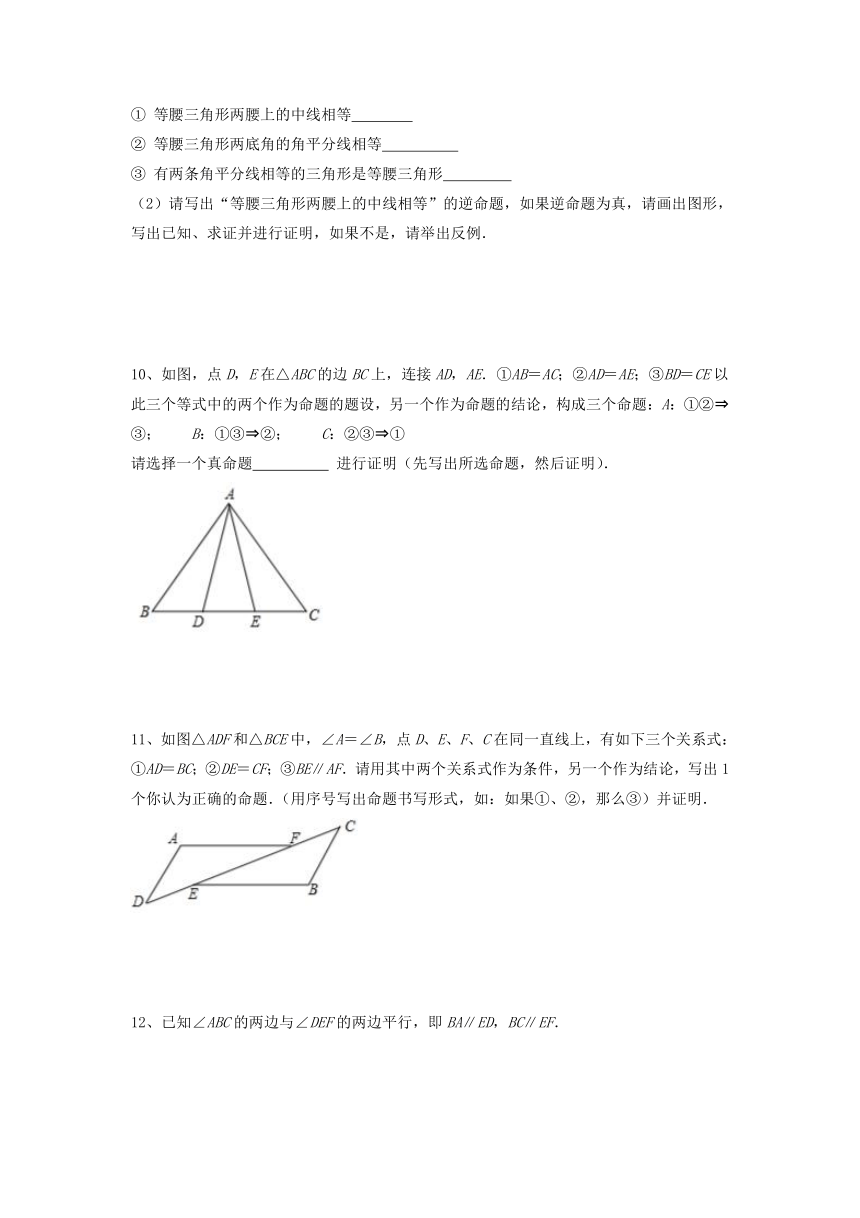
10、如图,点D,E在△ABC的边BC上,连接AD,AE.①AB=AC;②AD=AE;③BD=CE以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:A:①② ③; B:①③ ②; C:②③ ①
请选择一个真命题 进行证明(先写出所选命题,然后证明).
11、如图△ADF和△BCE中,∠A=∠B,点D、E、F、C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.请用其中两个关系式作为条件,另一个作为结论,写出1个你认为正确的命题.(用序号写出命题书写形式,如:如果①、②,那么③)并证明.
12、已知∠ABC的两边与∠DEF的两边平行,即BA∥ED,BC∥EF.
(1)如图①,若∠B=40°.则∠E= °.
(2)如图②,猜想∠B与∠E有怎样的关系?并说明理由.
(3)如图③,猜想∠B与∠E有怎样的关系?并说明理由.
(4)根据以上的情况,请你归纳概括出一个真命题.
13、在数学课上,林老师在黑板上画出如图所示的△ABD和△ACE两个三角形,并写出四个条件:①AB=AC;②AD=AE;③∠1=∠2;④∠B=∠C.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.
题设: ;结论: .(均填写序号)
证明: .
14、如图,B、A、E三点在同一直线上,(1)AD∥BC,(2)∠B=∠C,(3)AD平分∠EAC.
请你用其中两个作为条件,另一个作为结论,构造一个真命题,并证明.
已知: ;求证: 。
证明:
15、在学习了全等三角形和等边三角形的知识后,张老师出了如下一道题:如图,点B是线段AC上任意一点,分别以AB、BC为边在AC同一侧作等边△ABD和等边△BCE,连接CD、AE分别与BE和DB交于点N、M,连接MN.求证:△ABE≌△DBC.接着张老师又让学生分小组进行探究:你还能得出什么结论?精英小组探究的结论是:AM=DN
奋斗小组探究的结论是:△EMB≌△CNB.创新小组探究的结论是:MN∥AC.
(1)你认为哪一小组探究的结论是正确的?
(2)选择其中你认为正确的一种情形加以证明.
【参考答案】
1、下面是六个推断:
① 因为平角的两条边在一条直线上,所以直线是一个平角.
② 因为周角的两条边在一条射线上,所以射线是一个周角.
③ 因为扇形是圆的一部分,所以圆周的一部分是扇形.
④ 因为平行的线段没有交点,所以不相交的两条线段平行.
⑤ 因为正方形的边长都相等,所以边长相等的四边形是正方形.
⑥ 因为等腰三角形有两个内角相等,所以有两个内角相等的三角形是等腰三角形.
其中正确的结论有 个,其序号是 .
【解答】解:① 因为直线没有端点,所以直线不是平角,故此小题错误;
② 因为射线是一条线,所以射线不是角,故此小题错误;
③ 因为一条弧和经过这条弧两端的两条半径所围成的图形叫扇形,所以圆周的一部分不是扇形,故此小题错误;
④ 因为线段有两个端点,所以不相交的两条线段不一定平行,故此小题错误;
⑤ 因为边长相等的四边形有可能是菱形,所以此小题错误;
⑥ 符合等腰三角形的性质及判定定理,故此小题正确.
故正确的结论有1个,其序号是⑥.故答案为:1,⑥.
2、数学上往往是先有猜想,猜想被证明正确后便成为定理.黎曼猜想(也称黎曼假设)是100多年前由德国著名数学家黎曼提出的,它是世界上最重要的数学猜想之一.有大约1000个数学命题,一旦黎曼猜想得到证明,它们就必然成立.黎曼猜想与物理学、密码学也有深刻的联系.黎曼猜想与以下数学式有关:1+++…++…
当s=1时,上式就是所有正整数的倒数的和1+++…++…(*)
随着n的无限增加,(*)式中的第n项将无限接近于0,那么(*)式的值会比10大吗?会比10000大吗?
自然的感觉是“聚沙成塔”、“积少成多”,即设法把很多小小的项累加起来变大,下面是实现这个想法的一种组合法:1++(+)+(+++)+(+++++++)+…+
>1++(+)+(+++)+(+++++++)+…+
用这种方法可以判定(*)式中:
(1)从第一项1开始,一共 项的和就可以大于3;
(2)从第一项1开始,一共 项的和就可以大于6.
【解答】解:(1)∵1++(+)+(+++)+(+++++++)+…+
>1++(+)+(+++)+(+++++++)+…+,
∴1+×4=3,∵1+1+2+4+8=16,∴前面16项的和大于3,故答案为:16.
(2)当1+x×=6时,x=10,∴1+1+2+4+8+16+32+64+128+256+512=1024,
∴前面1024项的和大于6,故答案为:1024.
3、判断下列命题是真命题还是假命题;如果是假命题,请举一个反例
(1)两个锐角的和是锐角;
(2)若a>b,则a2>b2;
(3)若n是自然数,则代数式(3n+1)(3n+2)+1的值是3的倍数.
【解答】解:(1)假命题.反例为:40°与60°的和为100°;
(2)假命题.反例为:a=1,b=﹣3,但是a2=1<b2=9.
(3)真命题.∵(3n+1)(3n+2)+1=9n2+6n+3n+2+1=9n2+9n+3=3(3n2+3n+1),
又n为自然数,∴3(3n2+3n+1)为3的倍数.
4、请判断下列命题的真假性,若是假命题请举反例说明.
(1)若a>b,则a2>b2;
(2)两个无理数的和仍是无理数;
(3)若三角形三边a,b,c满足(a﹣b)(b﹣c)(c﹣a)=0,则三角形是等边三角形;
(4)若三条线段a,b,c满足a+b>c,则这三条线段a,b,c能够组成三角形.
【解答】解:(1)若a>b,则a2>b2,是假命题,例如:0>﹣1,但02<(﹣1)2;
(2)两个无理数的和仍是无理数,是假命题,例如:﹣+=0,和是有理数;
(3)若三角形三边a,b,c满足(a﹣b)(b﹣c)(c﹣a)=0,则三角形是等边三角形,是假命题,
例如:a=b,b≠c时,(a﹣b)(b﹣c)(c﹣a)=0,三角形是等腰三角形;
(4)若三条线段a,b,c满足a+b>c,则这三条线段a,b,c能够组成三角形,是假命题,
例如:三条线段a=3,b=2,c=1满足a+b>c,但这三条线段不能够组成三角形.
5、把下列命题改写成“如果…那么…”的形式.
(1)两直线平行,同位角相等;
(2)在同一个三角形中,等角对等边;
(3)同角的补角相等;
(4)两个无理数的积仍是无理数.
【解答】解:(1)如果两直线平行,那么同位角相等;
(2)在同一个三角形中,如果两个角相等,那么它们所对的边相等;
(3)如果两个角是同一个角的补角,那么这两个角相等;
(4)如果两个数是无理数,那么这两个数的积仍是无理数.
6、将下列命题改写成“如果…,那么…”的形式.
(1)能被2整除的数也能被4整除;
(2)相等的两个角是对顶角;
(3)若xy=0,则x=0;
(4)角平分线上的点到这个角两边的距离相等.
【解答】解:(1)如果一个数能被2整除,那么这个数也能被4整除;
(2)如果两个角相等,那么这两个角是对顶角;
(3)如果xy=0,那么x=0;
(4)如果一个点在角平分线上,那么它到角两边的距离相等.
7、下列定理中,哪些有逆定理?如果有逆定理,写出它的逆定理.
(1)全等三角形的对应角相等.
(2)同旁内角互补,两直线平行.
【解答】解:(1)全等三角形的对应角相等的逆命题是对应角相等的三角形是全等三角形,错误;
(2)同旁内角互补,两直线平行的逆命题是两直线平行,同旁内角互补,正确.
8、请写出下列命题的逆命题,并判断这些逆命题是否成立.
(1)同旁内角相等,两直线平行.
(2)如果两个角是直角,那么这两个角相等.
【解答】解:(1)同旁内角相等,两直线平行,逆命题是两直线平行,同旁内角相等,逆命题不成立;
(2)如果两个角是直角,那么这两个角相等,逆命题是如果两个角相等,那么两个角是直角,逆命题不成立.
9、对几何命题进行逆向思考是几何研究中的重要策略,我们知道,等腰三角形两腰上的高 线相等,那么等腰三角形两腰上的中线,两底角的角平分线也分别相等吗?它们的逆命 题会正确吗?
(1)请判断下列命题的真假,并在相应命题后面的括号内填上“真”或“假”.
① 等腰三角形两腰上的中线相等
② 等腰三角形两底角的角平分线相等
③ 有两条角平分线相等的三角形是等腰三角形
(2)请写出“等腰三角形两腰上的中线相等”的逆命题,如果逆命题为真,请画出图形,写出已知、求证并进行证明,如果不是,请举出反例.
【解答】解:(1)① 等腰三角形两腰上的中线相等是真命题;
② 等腰三角形两底角的角平分线相等是真命题;
③ 有两条角平分线相等的三角形是等腰三角形是真命题; 故答案为:真;真;真;
(2)逆命题是:有两边上的中线相等的三角形是等腰三角形;
已知:如图,△ABC中,BD,CE分别是AC,BC边上的中线,且BD=CE,
求证:△ABC是等腰三角形;
证明:连接DE,过点D作DF∥EC,交BC的延长线于点F,
∵BD,CE分别是AC,BC边上的中线,∴DE是△ABC的中位线,∴DE∥BC,∵DF∥EC,
∴四边形DECF是平行四边形,∴EC=DF,∵BD=CE,∴DF=BD,∴∠DBF=∠DFB,
∵DF∥EC,∴∠F=∠ECB,∴∠ECB=∠DBC,在△DBC与△ECB中,∴△DBC≌△ECB,
∴EB=DC,∴AB=AC,∴△ABC是等腰三角形.
10、如图,点D,E在△ABC的边BC上,连接AD,AE.①AB=AC;②AD=AE;③BD=CE以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:A:①② ③; B:①③ ②; C:②③ ①
请选择一个真命题 进行证明(先写出所选命题,然后证明).
【解答】已知:AB=AC,BD=CE,求证:AD=AE.
证明:∵AB=AC,∴∠B=∠C,在△ABD和△ACE中,,∴△ABD≌△ACE,∴AD=AE.
故答案为:①③②.
11、如图△ADF和△BCE中,∠A=∠B,点D、E、F、C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.请用其中两个关系式作为条件,另一个作为结论,写出1个你认为正确的命题.(用序号写出命题书写形式,如:如果①、②,那么③)并证明.
【解答】解:“如果①,③,那么②”,
证明:∵BE∥AF,∴∠AFD=∠BEC.∵AD=BC,∠A=∠B,
∴△ADF≌△BCE.∴DF=CE.∴DF﹣EF=CE﹣EF.即DE=CF.
对于“如果②,③,那么①”证明如下:
∵BE∥AF,∴∠AFD=∠BEC.∵DE=CF,∴DE+EF=CF+EF. 即DF=CE.
∵∠A=∠B,∴△ADF≌△BCE.∴AD=BC.
12、已知∠ABC的两边与∠DEF的两边平行,即BA∥ED,BC∥EF.
(1)如图①,若∠B=40°.则∠E= °.
(2)如图②,猜想∠B与∠E有怎样的关系?并说明理由.
(3)如图③,猜想∠B与∠E有怎样的关系?并说明理由.
(4)根据以上的情况,请你归纳概括出一个真命题.
【解答】解:(1)∵AB∥DE,∴∠B=∠DGC,∵BC∥EF,∴∠DGC=∠E,∴∠B=∠E=40°,故答案为:40;
(2)∠B=∠E,∵AB∥DE,∴∠B+∠BGE=180°,∵BC∥EF,∴∠BGE+∠E=180°,∴∠B=∠E;
(3)∠B+∠E=180°,
理由是:∵BA∥ED,BC∥EF,∴∠E=∠BGD,∠B+∠BGD=180°,∴∠B+∠E=180°;
(4)如果一个角的两边分别平行于另一个角的两边,则这两个角相等或互补.
13、在数学课上,林老师在黑板上画出如图所示的△ABD和△ACE两个三角形,并写出四个条件:①AB=AC;②AD=AE;③∠1=∠2;④∠B=∠C.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.
题设: ;结论: .(均填写序号)
证明: .
【解答】解:答案不唯一.如:
已知:在△ABD和△ACE中,AB=AC,AD=AE,∠1=∠2.求证:∠B=∠C.
证明:∵∠1=∠2,∴∠BAD=∠CAE.在△ABD和△ACE中,,∴△ABD≌△ACE.(SAS),
∴∠B=∠C(全等三角形对应边相等);故答案为:①②③;④.
∵∠1=∠2,∴∠BAD=∠CAE.在△ABD和△ACE中,,∴△ABD≌△ACE.(SAS),
∴∠B=∠C(全等三角形对应边相等).
14、如图,B、A、E三点在同一直线上,(1)AD∥BC,(2)∠B=∠C,(3)AD平分∠EAC.
请你用其中两个作为条件,另一个作为结论,构造一个真命题,并证明.
已知: ;求证: 。
证明:
【解答】解:命题:已知:AD∥BC,∠B=∠C,求证:AD平分∠EAC.
证明:∵AD∥BC,∴∠B=∠EAD,∠C=∠DAC.又∵∠B=∠C,∴∠EAD=∠DAC.即AD平分∠EAC.故是真命题.
故答案为:AD∥BC,∠B=∠C,AD平分∠EAC.
15、在学习了全等三角形和等边三角形的知识后,张老师出了如下一道题:如图,点B是线段AC上任意一点,分别以AB、BC为边在AC同一侧作等边△ABD和等边△BCE,连接CD、AE分别与BE和DB交于点N、M,连接MN.求证:△ABE≌△DBC.接着张老师又让学生分小组进行探究:你还能得出什么结论?精英小组探究的结论是:AM=DN
奋斗小组探究的结论是:△EMB≌△CNB.创新小组探究的结论是:MN∥AC.
(1)你认为哪一小组探究的结论是正确的?
(2)选择其中你认为正确的一种情形加以证明.
【解答】解:(1)三个小组探究的结论都正确;
(2)∵△ABD和△BCE是等边三角形,∴AB=BD,BC=BE,∠ABD=∠CBE=60°,∴∠ABE=∠DBC,
在△ABE与△DBC中,,∴△ABE≌△DBC(SAS),∴∠BAM=∠BDN,∠AEB=∠DCB,
在△ABM与△DBN中,,∴△ABM≌△DBN(AAS),∴AM=DN,BM=BN,
∵∠MBN=180°﹣60°﹣60°=60°,∴△BMN是等边三角形,∴∠BMN=60°,∴∠BMN=∠ABM,∴NM∥AC,
在△EMB与△CNB中,,∴△EMB≌△CNB(AAS).
1.2 定义与命题(1)定义与命题
【知识点-部分】
1、定义:用来说明一个名词或术语的意义的语句。
形式: ……叫做(是、为)……;
注:定义是严密的,避免使用含糊不清的术语。
2、命题:判断一件事情的句子,每个命题都由条件和结论两部分组成。
形式:如果(若)…那么(则)…
含义:(1)命题必须是一个完整的句子;(2)这个句子必须对某件事情作出肯定或否定的判断。
注:有些命题的条件和结论不够明显,要把命题改写成“如果……那么……”的形式,再找条件和结论。
1.2 定义与命题(2)真假命题、基本事实与定理
【知识点-部分】
一、真假命题、反证法
1、真命题:正确的命题(真命题在条件成立时,结论无一例外地成立)。
2、假命题:不正确的命题(假命题在条件成立时,结论却不能保证总是成立)。
3、反例:举一个例子,若具有命题的条件,而不具有命题的结论,这种例子称为反例。
注:(1)说明一个命题是真命题,需要根据定义、公理、定理进行严格证明才行;
(2)说明一个命题是假命题,举出一个反例即可。
4、证明的必要性:
(1)证明的定义:要判断一个命题是不是真命题,仅仅依靠经验、观察、实验和猜想是不够的,必须一步步、有根有据的进行推理。推理的过程叫做证明
(2)步骤:1) 理解题意:分清命题的条件(已知),结论(求证) 2)根据题意,画出图形;
3)结合图形,用符号语言写出“已知”和“求证 4)分析题意,探索证明思路; 5)写出证明过程;
方法:举出反例、推理证明、反证法
5、反证法:假设命题不成立,从这样的假设出发,经过推理得出和已知条件矛盾,或者与定义,公理,定理等矛
盾,从而得出假设命题不成立是错误的,即所求证的命题正确.
步骤:(1)反设(否定结论);(2)归谬(利用已知条件和反设,已学过的公理、定理、定义、法则,
进行推理,得出与已学过的公理、定理、或与已知条件,或与假设矛盾);
(3)写出结论(肯定原命题成立)。
二、公理与定理
一、公理-1、公理定义:通过长期实践总结出来,并且被人们公认的真命题叫做公理。
注:(1)公里是不需要推理证明的真命题; (2)公理可作为判断其他命题真假的依据。
2、常见公理:(1)同位角相等,两直线平行; (2)两直线平行,同位角相等;
(3)两边及其夹角对应相等的两个三角形全等; (4)两角及其夹边对应相等的两个三角形全等;
(5)三边对应相等的两个三角形全等; (6)全等三角形的对应边相等,对应角相等;
(7)两点确定一条直线; (8)等式的有关性质和不等式的有关性质都可以看做公理;
例如:“在等式或不等式中,一个量可以用它的等量来代替”简称为“等量代换”。
二、定理-1、定理:通过推理得到证实的真命题叫做定理。
注:(1)定理都是真命题,但真命题不一定都是定理; (2)定理可作为判断其他命题真假的依据。
【典型例题-精选部分】
1、下面是六个推断:
① 因为平角的两条边在一条直线上,所以直线是一个平角.
② 因为周角的两条边在一条射线上,所以射线是一个周角.
③ 因为扇形是圆的一部分,所以圆周的一部分是扇形.
④ 因为平行的线段没有交点,所以不相交的两条线段平行.
⑤ 因为正方形的边长都相等,所以边长相等的四边形是正方形.
⑥ 因为等腰三角形有两个内角相等,所以有两个内角相等的三角形是等腰三角形.
其中正确的结论有 个,其序号是 .
2、数学上往往是先有猜想,猜想被证明正确后便成为定理.黎曼猜想(也称黎曼假设)是100多年前由德国著名数学家黎曼提出的,它是世界上最重要的数学猜想之一.有大约1000个数学命题,一旦黎曼猜想得到证明,它们就必然成立.黎曼猜想与物理学、密码学也有深刻的联系.黎曼猜想与以下数学式有关:1+++…++…
当s=1时,上式就是所有正整数的倒数的和1+++…++…(*)
随着n的无限增加,(*)式中的第n项将无限接近于0,那么(*)式的值会比10大吗?会比10000大吗?
自然的感觉是“聚沙成塔”、“积少成多”,即设法把很多小小的项累加起来变大,下面是实现这个想法的一种组合法:1++(+)+(+++)+(+++++++)+…+
>1++(+)+(+++)+(+++++++)+…+
用这种方法可以判定(*)式中:
(1)从第一项1开始,一共 项的和就可以大于3;
(2)从第一项1开始,一共 项的和就可以大于6.
3、判断下列命题是真命题还是假命题;如果是假命题,请举一个反例
(1)两个锐角的和是锐角;
(2)若a>b,则a2>b2;
(3)若n是自然数,则代数式(3n+1)(3n+2)+1的值是3的倍数.
4、请判断下列命题的真假性,若是假命题请举反例说明.
(1)若a>b,则a2>b2;
(2)两个无理数的和仍是无理数;
(3)若三角形三边a,b,c满足(a﹣b)(b﹣c)(c﹣a)=0,则三角形是等边三角形;
(4)若三条线段a,b,c满足a+b>c,则这三条线段a,b,c能够组成三角形.
5、把下列命题改写成“如果…那么…”的形式.
(1)两直线平行,同位角相等;
(2)在同一个三角形中,等角对等边;
(3)同角的补角相等;
(4)两个无理数的积仍是无理数.
6、将下列命题改写成“如果…,那么…”的形式.
(1)能被2整除的数也能被4整除;
(2)相等的两个角是对顶角;
(3)若xy=0,则x=0;
(4)角平分线上的点到这个角两边的距离相等.
7、下列定理中,哪些有逆定理?如果有逆定理,写出它的逆定理.
(1)全等三角形的对应角相等.
(2)同旁内角互补,两直线平行.
8、请写出下列命题的逆命题,并判断这些逆命题是否成立.
(1)同旁内角相等,两直线平行.
(2)如果两个角是直角,那么这两个角相等.
9、对几何命题进行逆向思考是几何研究中的重要策略,我们知道,等腰三角形两腰上的高 线相等,那么等腰三角形两腰上的中线,两底角的角平分线也分别相等吗?它们的逆命 题会正确吗?
(1)请判断下列命题的真假,并在相应命题后面的括号内填上“真”或“假”.
① 等腰三角形两腰上的中线相等
② 等腰三角形两底角的角平分线相等
③ 有两条角平分线相等的三角形是等腰三角形
(2)请写出“等腰三角形两腰上的中线相等”的逆命题,如果逆命题为真,请画出图形,写出已知、求证并进行证明,如果不是,请举出反例.
10、如图,点D,E在△ABC的边BC上,连接AD,AE.①AB=AC;②AD=AE;③BD=CE以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:A:①② ③; B:①③ ②; C:②③ ①
请选择一个真命题 进行证明(先写出所选命题,然后证明).
11、如图△ADF和△BCE中,∠A=∠B,点D、E、F、C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.请用其中两个关系式作为条件,另一个作为结论,写出1个你认为正确的命题.(用序号写出命题书写形式,如:如果①、②,那么③)并证明.
12、已知∠ABC的两边与∠DEF的两边平行,即BA∥ED,BC∥EF.
(1)如图①,若∠B=40°.则∠E= °.
(2)如图②,猜想∠B与∠E有怎样的关系?并说明理由.
(3)如图③,猜想∠B与∠E有怎样的关系?并说明理由.
(4)根据以上的情况,请你归纳概括出一个真命题.
13、在数学课上,林老师在黑板上画出如图所示的△ABD和△ACE两个三角形,并写出四个条件:①AB=AC;②AD=AE;③∠1=∠2;④∠B=∠C.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.
题设: ;结论: .(均填写序号)
证明: .
14、如图,B、A、E三点在同一直线上,(1)AD∥BC,(2)∠B=∠C,(3)AD平分∠EAC.
请你用其中两个作为条件,另一个作为结论,构造一个真命题,并证明.
已知: ;求证: 。
证明:
15、在学习了全等三角形和等边三角形的知识后,张老师出了如下一道题:如图,点B是线段AC上任意一点,分别以AB、BC为边在AC同一侧作等边△ABD和等边△BCE,连接CD、AE分别与BE和DB交于点N、M,连接MN.求证:△ABE≌△DBC.接着张老师又让学生分小组进行探究:你还能得出什么结论?精英小组探究的结论是:AM=DN
奋斗小组探究的结论是:△EMB≌△CNB.创新小组探究的结论是:MN∥AC.
(1)你认为哪一小组探究的结论是正确的?
(2)选择其中你认为正确的一种情形加以证明.
【参考答案】
1、下面是六个推断:
① 因为平角的两条边在一条直线上,所以直线是一个平角.
② 因为周角的两条边在一条射线上,所以射线是一个周角.
③ 因为扇形是圆的一部分,所以圆周的一部分是扇形.
④ 因为平行的线段没有交点,所以不相交的两条线段平行.
⑤ 因为正方形的边长都相等,所以边长相等的四边形是正方形.
⑥ 因为等腰三角形有两个内角相等,所以有两个内角相等的三角形是等腰三角形.
其中正确的结论有 个,其序号是 .
【解答】解:① 因为直线没有端点,所以直线不是平角,故此小题错误;
② 因为射线是一条线,所以射线不是角,故此小题错误;
③ 因为一条弧和经过这条弧两端的两条半径所围成的图形叫扇形,所以圆周的一部分不是扇形,故此小题错误;
④ 因为线段有两个端点,所以不相交的两条线段不一定平行,故此小题错误;
⑤ 因为边长相等的四边形有可能是菱形,所以此小题错误;
⑥ 符合等腰三角形的性质及判定定理,故此小题正确.
故正确的结论有1个,其序号是⑥.故答案为:1,⑥.
2、数学上往往是先有猜想,猜想被证明正确后便成为定理.黎曼猜想(也称黎曼假设)是100多年前由德国著名数学家黎曼提出的,它是世界上最重要的数学猜想之一.有大约1000个数学命题,一旦黎曼猜想得到证明,它们就必然成立.黎曼猜想与物理学、密码学也有深刻的联系.黎曼猜想与以下数学式有关:1+++…++…
当s=1时,上式就是所有正整数的倒数的和1+++…++…(*)
随着n的无限增加,(*)式中的第n项将无限接近于0,那么(*)式的值会比10大吗?会比10000大吗?
自然的感觉是“聚沙成塔”、“积少成多”,即设法把很多小小的项累加起来变大,下面是实现这个想法的一种组合法:1++(+)+(+++)+(+++++++)+…+
>1++(+)+(+++)+(+++++++)+…+
用这种方法可以判定(*)式中:
(1)从第一项1开始,一共 项的和就可以大于3;
(2)从第一项1开始,一共 项的和就可以大于6.
【解答】解:(1)∵1++(+)+(+++)+(+++++++)+…+
>1++(+)+(+++)+(+++++++)+…+,
∴1+×4=3,∵1+1+2+4+8=16,∴前面16项的和大于3,故答案为:16.
(2)当1+x×=6时,x=10,∴1+1+2+4+8+16+32+64+128+256+512=1024,
∴前面1024项的和大于6,故答案为:1024.
3、判断下列命题是真命题还是假命题;如果是假命题,请举一个反例
(1)两个锐角的和是锐角;
(2)若a>b,则a2>b2;
(3)若n是自然数,则代数式(3n+1)(3n+2)+1的值是3的倍数.
【解答】解:(1)假命题.反例为:40°与60°的和为100°;
(2)假命题.反例为:a=1,b=﹣3,但是a2=1<b2=9.
(3)真命题.∵(3n+1)(3n+2)+1=9n2+6n+3n+2+1=9n2+9n+3=3(3n2+3n+1),
又n为自然数,∴3(3n2+3n+1)为3的倍数.
4、请判断下列命题的真假性,若是假命题请举反例说明.
(1)若a>b,则a2>b2;
(2)两个无理数的和仍是无理数;
(3)若三角形三边a,b,c满足(a﹣b)(b﹣c)(c﹣a)=0,则三角形是等边三角形;
(4)若三条线段a,b,c满足a+b>c,则这三条线段a,b,c能够组成三角形.
【解答】解:(1)若a>b,则a2>b2,是假命题,例如:0>﹣1,但02<(﹣1)2;
(2)两个无理数的和仍是无理数,是假命题,例如:﹣+=0,和是有理数;
(3)若三角形三边a,b,c满足(a﹣b)(b﹣c)(c﹣a)=0,则三角形是等边三角形,是假命题,
例如:a=b,b≠c时,(a﹣b)(b﹣c)(c﹣a)=0,三角形是等腰三角形;
(4)若三条线段a,b,c满足a+b>c,则这三条线段a,b,c能够组成三角形,是假命题,
例如:三条线段a=3,b=2,c=1满足a+b>c,但这三条线段不能够组成三角形.
5、把下列命题改写成“如果…那么…”的形式.
(1)两直线平行,同位角相等;
(2)在同一个三角形中,等角对等边;
(3)同角的补角相等;
(4)两个无理数的积仍是无理数.
【解答】解:(1)如果两直线平行,那么同位角相等;
(2)在同一个三角形中,如果两个角相等,那么它们所对的边相等;
(3)如果两个角是同一个角的补角,那么这两个角相等;
(4)如果两个数是无理数,那么这两个数的积仍是无理数.
6、将下列命题改写成“如果…,那么…”的形式.
(1)能被2整除的数也能被4整除;
(2)相等的两个角是对顶角;
(3)若xy=0,则x=0;
(4)角平分线上的点到这个角两边的距离相等.
【解答】解:(1)如果一个数能被2整除,那么这个数也能被4整除;
(2)如果两个角相等,那么这两个角是对顶角;
(3)如果xy=0,那么x=0;
(4)如果一个点在角平分线上,那么它到角两边的距离相等.
7、下列定理中,哪些有逆定理?如果有逆定理,写出它的逆定理.
(1)全等三角形的对应角相等.
(2)同旁内角互补,两直线平行.
【解答】解:(1)全等三角形的对应角相等的逆命题是对应角相等的三角形是全等三角形,错误;
(2)同旁内角互补,两直线平行的逆命题是两直线平行,同旁内角互补,正确.
8、请写出下列命题的逆命题,并判断这些逆命题是否成立.
(1)同旁内角相等,两直线平行.
(2)如果两个角是直角,那么这两个角相等.
【解答】解:(1)同旁内角相等,两直线平行,逆命题是两直线平行,同旁内角相等,逆命题不成立;
(2)如果两个角是直角,那么这两个角相等,逆命题是如果两个角相等,那么两个角是直角,逆命题不成立.
9、对几何命题进行逆向思考是几何研究中的重要策略,我们知道,等腰三角形两腰上的高 线相等,那么等腰三角形两腰上的中线,两底角的角平分线也分别相等吗?它们的逆命 题会正确吗?
(1)请判断下列命题的真假,并在相应命题后面的括号内填上“真”或“假”.
① 等腰三角形两腰上的中线相等
② 等腰三角形两底角的角平分线相等
③ 有两条角平分线相等的三角形是等腰三角形
(2)请写出“等腰三角形两腰上的中线相等”的逆命题,如果逆命题为真,请画出图形,写出已知、求证并进行证明,如果不是,请举出反例.
【解答】解:(1)① 等腰三角形两腰上的中线相等是真命题;
② 等腰三角形两底角的角平分线相等是真命题;
③ 有两条角平分线相等的三角形是等腰三角形是真命题; 故答案为:真;真;真;
(2)逆命题是:有两边上的中线相等的三角形是等腰三角形;
已知:如图,△ABC中,BD,CE分别是AC,BC边上的中线,且BD=CE,
求证:△ABC是等腰三角形;
证明:连接DE,过点D作DF∥EC,交BC的延长线于点F,
∵BD,CE分别是AC,BC边上的中线,∴DE是△ABC的中位线,∴DE∥BC,∵DF∥EC,
∴四边形DECF是平行四边形,∴EC=DF,∵BD=CE,∴DF=BD,∴∠DBF=∠DFB,
∵DF∥EC,∴∠F=∠ECB,∴∠ECB=∠DBC,在△DBC与△ECB中,∴△DBC≌△ECB,
∴EB=DC,∴AB=AC,∴△ABC是等腰三角形.
10、如图,点D,E在△ABC的边BC上,连接AD,AE.①AB=AC;②AD=AE;③BD=CE以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:A:①② ③; B:①③ ②; C:②③ ①
请选择一个真命题 进行证明(先写出所选命题,然后证明).
【解答】已知:AB=AC,BD=CE,求证:AD=AE.
证明:∵AB=AC,∴∠B=∠C,在△ABD和△ACE中,,∴△ABD≌△ACE,∴AD=AE.
故答案为:①③②.
11、如图△ADF和△BCE中,∠A=∠B,点D、E、F、C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.请用其中两个关系式作为条件,另一个作为结论,写出1个你认为正确的命题.(用序号写出命题书写形式,如:如果①、②,那么③)并证明.
【解答】解:“如果①,③,那么②”,
证明:∵BE∥AF,∴∠AFD=∠BEC.∵AD=BC,∠A=∠B,
∴△ADF≌△BCE.∴DF=CE.∴DF﹣EF=CE﹣EF.即DE=CF.
对于“如果②,③,那么①”证明如下:
∵BE∥AF,∴∠AFD=∠BEC.∵DE=CF,∴DE+EF=CF+EF. 即DF=CE.
∵∠A=∠B,∴△ADF≌△BCE.∴AD=BC.
12、已知∠ABC的两边与∠DEF的两边平行,即BA∥ED,BC∥EF.
(1)如图①,若∠B=40°.则∠E= °.
(2)如图②,猜想∠B与∠E有怎样的关系?并说明理由.
(3)如图③,猜想∠B与∠E有怎样的关系?并说明理由.
(4)根据以上的情况,请你归纳概括出一个真命题.
【解答】解:(1)∵AB∥DE,∴∠B=∠DGC,∵BC∥EF,∴∠DGC=∠E,∴∠B=∠E=40°,故答案为:40;
(2)∠B=∠E,∵AB∥DE,∴∠B+∠BGE=180°,∵BC∥EF,∴∠BGE+∠E=180°,∴∠B=∠E;
(3)∠B+∠E=180°,
理由是:∵BA∥ED,BC∥EF,∴∠E=∠BGD,∠B+∠BGD=180°,∴∠B+∠E=180°;
(4)如果一个角的两边分别平行于另一个角的两边,则这两个角相等或互补.
13、在数学课上,林老师在黑板上画出如图所示的△ABD和△ACE两个三角形,并写出四个条件:①AB=AC;②AD=AE;③∠1=∠2;④∠B=∠C.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.
题设: ;结论: .(均填写序号)
证明: .
【解答】解:答案不唯一.如:
已知:在△ABD和△ACE中,AB=AC,AD=AE,∠1=∠2.求证:∠B=∠C.
证明:∵∠1=∠2,∴∠BAD=∠CAE.在△ABD和△ACE中,,∴△ABD≌△ACE.(SAS),
∴∠B=∠C(全等三角形对应边相等);故答案为:①②③;④.
∵∠1=∠2,∴∠BAD=∠CAE.在△ABD和△ACE中,,∴△ABD≌△ACE.(SAS),
∴∠B=∠C(全等三角形对应边相等).
14、如图,B、A、E三点在同一直线上,(1)AD∥BC,(2)∠B=∠C,(3)AD平分∠EAC.
请你用其中两个作为条件,另一个作为结论,构造一个真命题,并证明.
已知: ;求证: 。
证明:
【解答】解:命题:已知:AD∥BC,∠B=∠C,求证:AD平分∠EAC.
证明:∵AD∥BC,∴∠B=∠EAD,∠C=∠DAC.又∵∠B=∠C,∴∠EAD=∠DAC.即AD平分∠EAC.故是真命题.
故答案为:AD∥BC,∠B=∠C,AD平分∠EAC.
15、在学习了全等三角形和等边三角形的知识后,张老师出了如下一道题:如图,点B是线段AC上任意一点,分别以AB、BC为边在AC同一侧作等边△ABD和等边△BCE,连接CD、AE分别与BE和DB交于点N、M,连接MN.求证:△ABE≌△DBC.接着张老师又让学生分小组进行探究:你还能得出什么结论?精英小组探究的结论是:AM=DN
奋斗小组探究的结论是:△EMB≌△CNB.创新小组探究的结论是:MN∥AC.
(1)你认为哪一小组探究的结论是正确的?
(2)选择其中你认为正确的一种情形加以证明.
【解答】解:(1)三个小组探究的结论都正确;
(2)∵△ABD和△BCE是等边三角形,∴AB=BD,BC=BE,∠ABD=∠CBE=60°,∴∠ABE=∠DBC,
在△ABE与△DBC中,,∴△ABE≌△DBC(SAS),∴∠BAM=∠BDN,∠AEB=∠DCB,
在△ABM与△DBN中,,∴△ABM≌△DBN(AAS),∴AM=DN,BM=BN,
∵∠MBN=180°﹣60°﹣60°=60°,∴△BMN是等边三角形,∴∠BMN=60°,∴∠BMN=∠ABM,∴NM∥AC,
在△EMB与△CNB中,,∴△EMB≌△CNB(AAS).
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
