2.3等腰三角形性质2 课件(共19张PPT)
文档属性
| 名称 | 2.3等腰三角形性质2 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 364.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-08 19:26:13 | ||
图片预览

文档简介
(共19张PPT)
2.3 等腰三角形的性质定理 2
等腰三角形的轴对称性------等腰三角形三线合一
浙教版八上
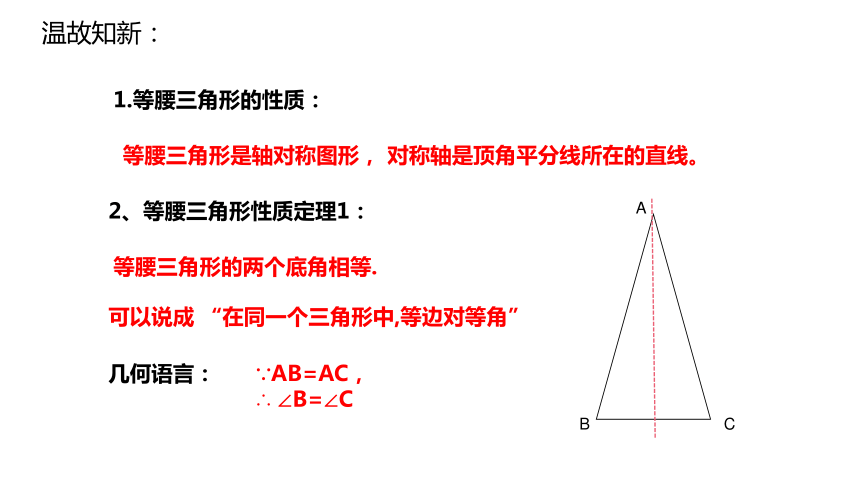
1.等腰三角形的性质:
等腰三角形是轴对称图形, 对称轴是顶角平分线所在的直线。
2、等腰三角形性质定理1:
等腰三角形的两个底角相等.
可以说成 “在同一个三角形中,等边对等角”
几何语言:
∵AB=AC,
∴ ∠B=∠C
温故知新:
A
B
C
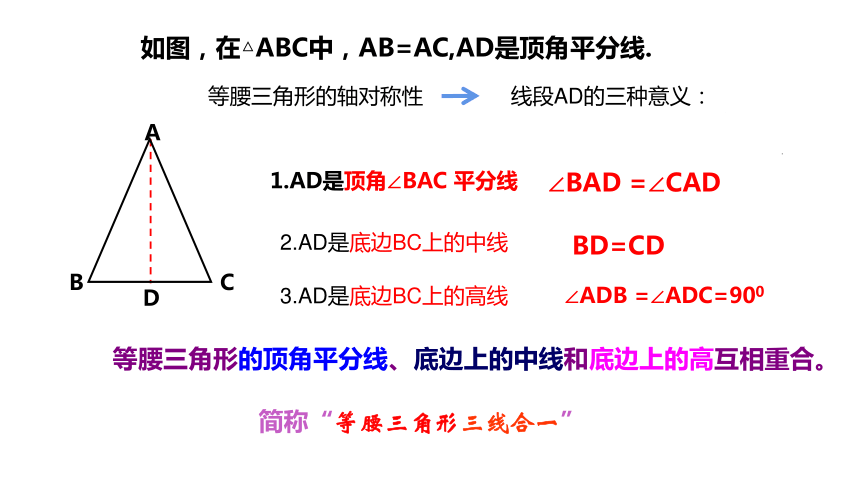
如图,在△ABC中,AB=AC,AD是顶角平分线.
A
B
C
D
BD=CD
∠BAD =∠CAD
∠ADB =∠ADC=900
线段AD的三种意义:
1.AD是顶角∠BAC 平分线
2.AD是底边BC上的中线
3.AD是底边BC上的高线
.
.
等腰三角形的轴对称性
等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合。
简称“等腰三角形三线合一”
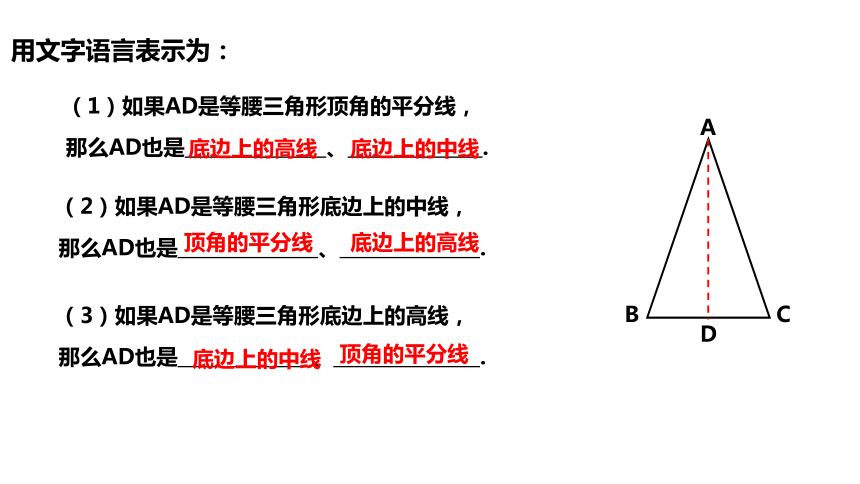
用文字语言表示为:
(1)如果AD是等腰三角形顶角的平分线,
那么AD也是 、 .
(2)如果AD是等腰三角形底边上的中线,
那么AD也是 、 .
(3)如果AD是等腰三角形底边上的高线,
那么AD也是 、 .
A
B
C
D
底边上的高线
底边上的中线
顶角的平分线
底边上的高线
底边上的中线
顶角的平分线
A
B
C
D
A
B
C
D
┓
A
B
C
D
A
B
C
D
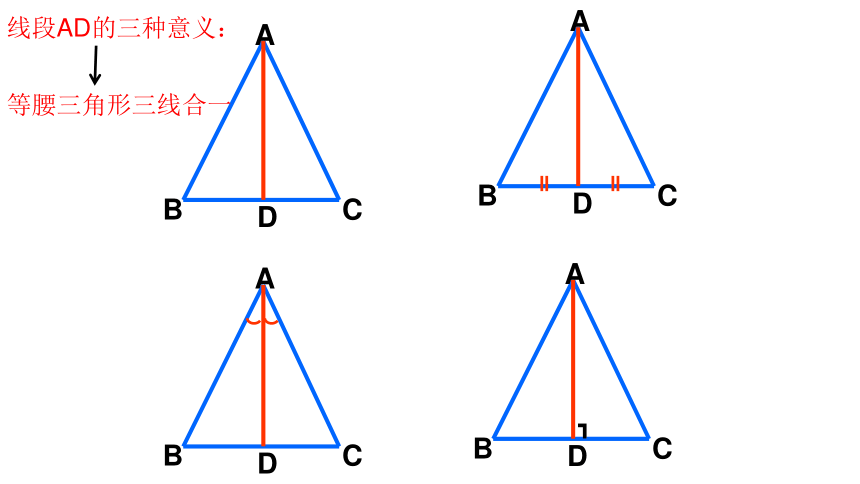
线段AD的三种意义:
等腰三角形三线合一
A
D
C
B
1
2
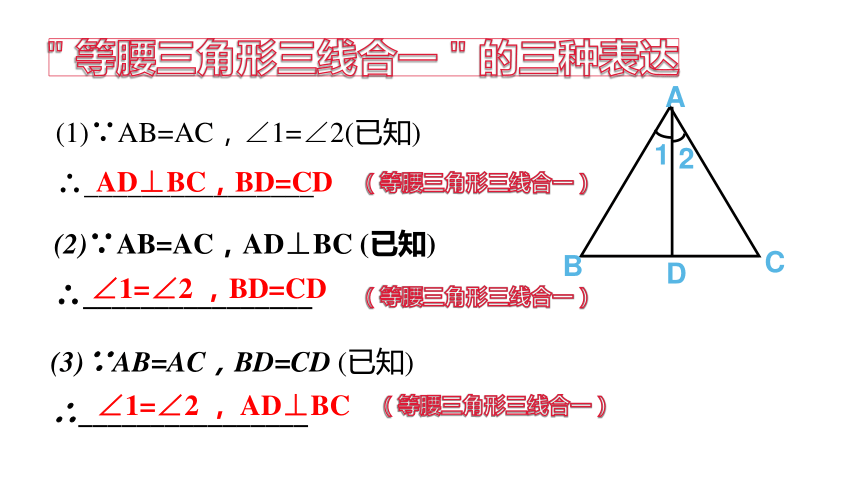
(1)∵AB=AC,∠1=∠2(已知)
∴________________
"等腰三角形三线合一"的三种表达
AD⊥BC,BD=CD
(2)∵AB=AC,AD⊥BC (已知)
∴________________
∠1=∠2 ,BD=CD
(3)∵AB=AC,BD=CD (已知)
∴________________
∠1=∠2 , AD⊥BC
(等腰三角形三线合一)
(等腰三角形三线合一)
(等腰三角形三线合一)
等腰
三角形
顶角平分线
底边上的高线
底边上的中线
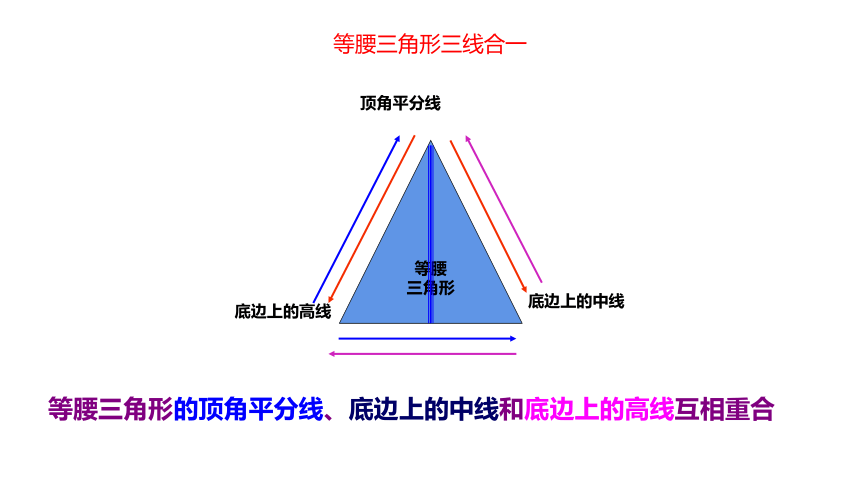
等腰三角形三线合一
等腰三角形的顶角平分线、底边上的中线和底边上的高线互相重合
等腰三角形的顶角平分线、底边上的中线和底边上的高线互相重合,
等腰三角形腰上的高线,腰上的中线,底角的平分线不一定互相重合。
等腰三角形(腰≠底边)
等边三角形(腰=底边)
非等腰三角形
非等腰三角形一边上的高线,该边上的中线,该边所对的角的平分线两两不重合
┐
┐
┐
┐
┐
┐
1、等腰三角形的角平分线、中线和高线互相重合。
2、等腰三角形的顶角平分线一定垂直底边。
3、等腰三角形的角平分线、高线和中线的
总数一共能画出9条。
4、等腰三角形底边上的中线一定垂直于底边。
1.判断对错
(X)
(√)
(X)
(√)
学以致用:
例1: 如图,已知点D在△ABC 的内部,连结AD、BD、CD,若AD平分∠BAC,∠ADB=∠ADC,求证:AD⊥BC.
证明:如图,延长AD,交BC于点E
∵AD平分∠BAC,∴∠BAD=∠CAD
在△ABD 和△ACD 中
‘
∴ △ABD ≌ △ACD (ASA)
∴AB=AC
∵AE平分∠BAC
∴AE⊥BC
即AD⊥BC(等腰三角形的三线合一)
E
例2 已知线段a, h,用直尺和圆规作等腰三角形ABC,使底边BC=a, BC边上的高为h.
h
a
作法:
1.作线段BC=a.
2.作BC的中垂线m,交BC于点D.
3.在直线 m上截取DA=h,连接AB,AC.
△ABC就是所求的等腰三角形.
D
B
C
h
A
1、等腰三角形的两个底角相等.
或 “在同一个三角形中,等边对等角”
简称“等腰三角形三线合一”
2、等腰三角形的顶角平分线、底边上的中线 和底边上的高互相重合.
归纳小结:
10
50°
4
当堂检测:
夯实基础,稳扎稳打
1.如图,在△ABC中,AB=AC.
(1)若AD平分∠BAC,BD=4, 则CD= .
(2)若BD=CD,∠BAC=100°,则∠CAD= .
(3)若AD⊥BC于点D,CD=5,则BC= .
.
2.如图,为了让电线杆垂直于地面,工程人员的操作方法通常是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC,当固定点B,C到杆脚E的距离相等,且B,E,C在同一直线上时,电线杆DE就垂直于BC.工程人员这种操作方法的依据是( )
A.等边对等角 B.垂线段最短
C.等腰三角形“三线合一” D.线段垂直平分线上的点
到这条线段两端点的距离相等
C
.
3.如图,房屋的顶角∠BAC=100°,过屋顶A的立柱AD⊥BC,屋椽AB=AC, 求顶架上∠B、∠C、∠BAD、∠CAD的度数。
解:在△ABC中,
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
=40°
又∵AD⊥BC(已知)
∴∠BAD=∠CAD(等腰三角形三线合一)
∴∠BAD=∠CAD=50°
A
B
D
C
∟
4.如图,AD是等边△ABC的中线,点E在AC上,AD=AE,
则∠EDC的度数为( )
A 150 B 200 C 250 D 300
A
连续递推,豁然开朗
A
B
C
D
E
等边三角形--------每个内角都是600
5.在△ABC中,AB=AC,D是BC边上的中点,
DF⊥AC于F DE ⊥ AB 于E .求证:DE=DF。
A
B
C
D
E
F
方法一:证明: ∵DE⊥AB,DF⊥AC(已知)
∴∠BED=∠CFD
又∵D是BC中点(已知)
∴BD=DC
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
在△DBE与△DCF中
∠DEB=∠DFC(已证)
∠B=∠C(已证)
BD=DC(已证)
∴ △BDE ≌ △CDF(AAS)
∴DE=DF
方法二:连AD 。
∵AB=AC,BD=DC(已知)
∴AD是∠BAC的平分线。
(等腰三角形三线合一)
又∵DE⊥AB DF⊥AC
∴DE=DF
(角平分线上的点到这个
角的两边距离相等)
6.如图,点D,E在BC上,AB=AC,AD=AE,
求证:BD=CE
法1
∵AB=AC , AD=AE
∴∠B=∠C , ∠ADE=∠AED
在△ABE和△ACD中
∴△ABE≌△ACD(AAS)
∴BE=CD
∴BE-DE=CD-DE
即BD=CE
。
6.如图,点D,E在BC上,AB=AC,AD=AE,求证:BD=CE
H
过A作AH ⊥ BC于H
∵ AB=AC , AD=AE
∴ BH=CH , DH=EH
∴BH-DH=CH-EH
即BD=CE
法2
等量减等量,其差相等;等量加等量,其和相等。
2.3 等腰三角形的性质定理 2
等腰三角形的轴对称性------等腰三角形三线合一
浙教版八上
1.等腰三角形的性质:
等腰三角形是轴对称图形, 对称轴是顶角平分线所在的直线。
2、等腰三角形性质定理1:
等腰三角形的两个底角相等.
可以说成 “在同一个三角形中,等边对等角”
几何语言:
∵AB=AC,
∴ ∠B=∠C
温故知新:
A
B
C
如图,在△ABC中,AB=AC,AD是顶角平分线.
A
B
C
D
BD=CD
∠BAD =∠CAD
∠ADB =∠ADC=900
线段AD的三种意义:
1.AD是顶角∠BAC 平分线
2.AD是底边BC上的中线
3.AD是底边BC上的高线
.
.
等腰三角形的轴对称性
等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合。
简称“等腰三角形三线合一”
用文字语言表示为:
(1)如果AD是等腰三角形顶角的平分线,
那么AD也是 、 .
(2)如果AD是等腰三角形底边上的中线,
那么AD也是 、 .
(3)如果AD是等腰三角形底边上的高线,
那么AD也是 、 .
A
B
C
D
底边上的高线
底边上的中线
顶角的平分线
底边上的高线
底边上的中线
顶角的平分线
A
B
C
D
A
B
C
D
┓
A
B
C
D
A
B
C
D
线段AD的三种意义:
等腰三角形三线合一
A
D
C
B
1
2
(1)∵AB=AC,∠1=∠2(已知)
∴________________
"等腰三角形三线合一"的三种表达
AD⊥BC,BD=CD
(2)∵AB=AC,AD⊥BC (已知)
∴________________
∠1=∠2 ,BD=CD
(3)∵AB=AC,BD=CD (已知)
∴________________
∠1=∠2 , AD⊥BC
(等腰三角形三线合一)
(等腰三角形三线合一)
(等腰三角形三线合一)
等腰
三角形
顶角平分线
底边上的高线
底边上的中线
等腰三角形三线合一
等腰三角形的顶角平分线、底边上的中线和底边上的高线互相重合
等腰三角形的顶角平分线、底边上的中线和底边上的高线互相重合,
等腰三角形腰上的高线,腰上的中线,底角的平分线不一定互相重合。
等腰三角形(腰≠底边)
等边三角形(腰=底边)
非等腰三角形
非等腰三角形一边上的高线,该边上的中线,该边所对的角的平分线两两不重合
┐
┐
┐
┐
┐
┐
1、等腰三角形的角平分线、中线和高线互相重合。
2、等腰三角形的顶角平分线一定垂直底边。
3、等腰三角形的角平分线、高线和中线的
总数一共能画出9条。
4、等腰三角形底边上的中线一定垂直于底边。
1.判断对错
(X)
(√)
(X)
(√)
学以致用:
例1: 如图,已知点D在△ABC 的内部,连结AD、BD、CD,若AD平分∠BAC,∠ADB=∠ADC,求证:AD⊥BC.
证明:如图,延长AD,交BC于点E
∵AD平分∠BAC,∴∠BAD=∠CAD
在△ABD 和△ACD 中
‘
∴ △ABD ≌ △ACD (ASA)
∴AB=AC
∵AE平分∠BAC
∴AE⊥BC
即AD⊥BC(等腰三角形的三线合一)
E
例2 已知线段a, h,用直尺和圆规作等腰三角形ABC,使底边BC=a, BC边上的高为h.
h
a
作法:
1.作线段BC=a.
2.作BC的中垂线m,交BC于点D.
3.在直线 m上截取DA=h,连接AB,AC.
△ABC就是所求的等腰三角形.
D
B
C
h
A
1、等腰三角形的两个底角相等.
或 “在同一个三角形中,等边对等角”
简称“等腰三角形三线合一”
2、等腰三角形的顶角平分线、底边上的中线 和底边上的高互相重合.
归纳小结:
10
50°
4
当堂检测:
夯实基础,稳扎稳打
1.如图,在△ABC中,AB=AC.
(1)若AD平分∠BAC,BD=4, 则CD= .
(2)若BD=CD,∠BAC=100°,则∠CAD= .
(3)若AD⊥BC于点D,CD=5,则BC= .
.
2.如图,为了让电线杆垂直于地面,工程人员的操作方法通常是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC,当固定点B,C到杆脚E的距离相等,且B,E,C在同一直线上时,电线杆DE就垂直于BC.工程人员这种操作方法的依据是( )
A.等边对等角 B.垂线段最短
C.等腰三角形“三线合一” D.线段垂直平分线上的点
到这条线段两端点的距离相等
C
.
3.如图,房屋的顶角∠BAC=100°,过屋顶A的立柱AD⊥BC,屋椽AB=AC, 求顶架上∠B、∠C、∠BAD、∠CAD的度数。
解:在△ABC中,
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
=40°
又∵AD⊥BC(已知)
∴∠BAD=∠CAD(等腰三角形三线合一)
∴∠BAD=∠CAD=50°
A
B
D
C
∟
4.如图,AD是等边△ABC的中线,点E在AC上,AD=AE,
则∠EDC的度数为( )
A 150 B 200 C 250 D 300
A
连续递推,豁然开朗
A
B
C
D
E
等边三角形--------每个内角都是600
5.在△ABC中,AB=AC,D是BC边上的中点,
DF⊥AC于F DE ⊥ AB 于E .求证:DE=DF。
A
B
C
D
E
F
方法一:证明: ∵DE⊥AB,DF⊥AC(已知)
∴∠BED=∠CFD
又∵D是BC中点(已知)
∴BD=DC
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
在△DBE与△DCF中
∠DEB=∠DFC(已证)
∠B=∠C(已证)
BD=DC(已证)
∴ △BDE ≌ △CDF(AAS)
∴DE=DF
方法二:连AD 。
∵AB=AC,BD=DC(已知)
∴AD是∠BAC的平分线。
(等腰三角形三线合一)
又∵DE⊥AB DF⊥AC
∴DE=DF
(角平分线上的点到这个
角的两边距离相等)
6.如图,点D,E在BC上,AB=AC,AD=AE,
求证:BD=CE
法1
∵AB=AC , AD=AE
∴∠B=∠C , ∠ADE=∠AED
在△ABE和△ACD中
∴△ABE≌△ACD(AAS)
∴BE=CD
∴BE-DE=CD-DE
即BD=CE
。
6.如图,点D,E在BC上,AB=AC,AD=AE,求证:BD=CE
H
过A作AH ⊥ BC于H
∵ AB=AC , AD=AE
∴ BH=CH , DH=EH
∴BH-DH=CH-EH
即BD=CE
法2
等量减等量,其差相等;等量加等量,其和相等。
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
