2.3等腰三角形的性质 (1) 公开课

课件23张PPT。2.3等腰三角形的
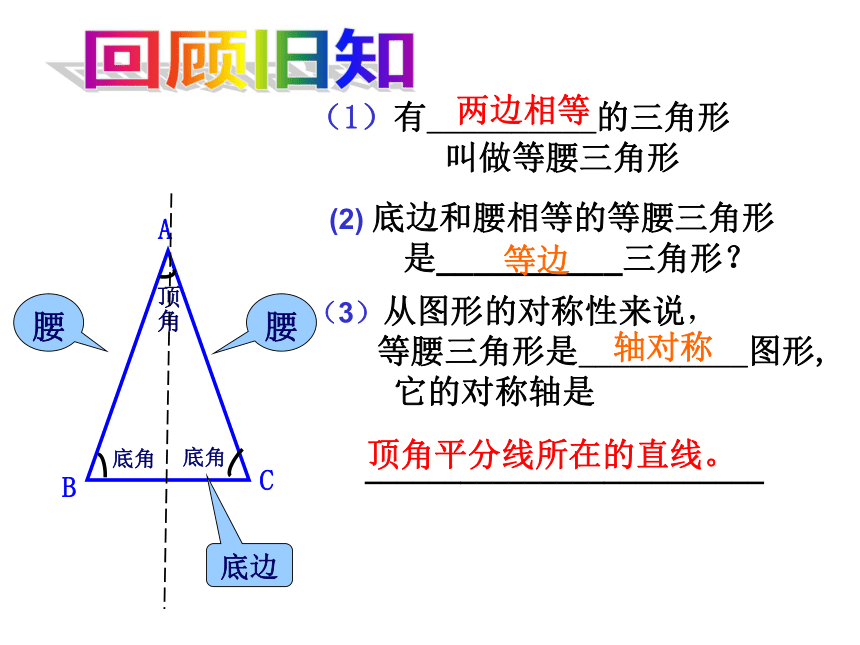
性质定理（1）有__________的三角形
叫做等腰三角形底边
(1)
（3）从图形的对称性来说，
等腰三角形是__________图形,
它的对称轴是
_________________________
顶角平分线所在的直线。


(2) 底边和腰相等的等腰三角形
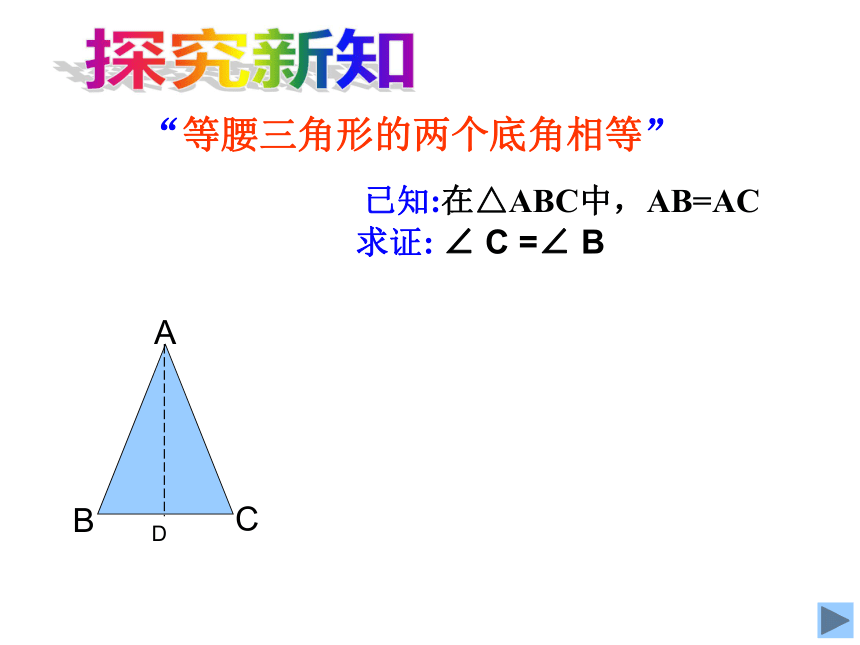
是__________三角形？等边两边相等轴对称回顾旧知 已知:在△ABC中，AB=AC
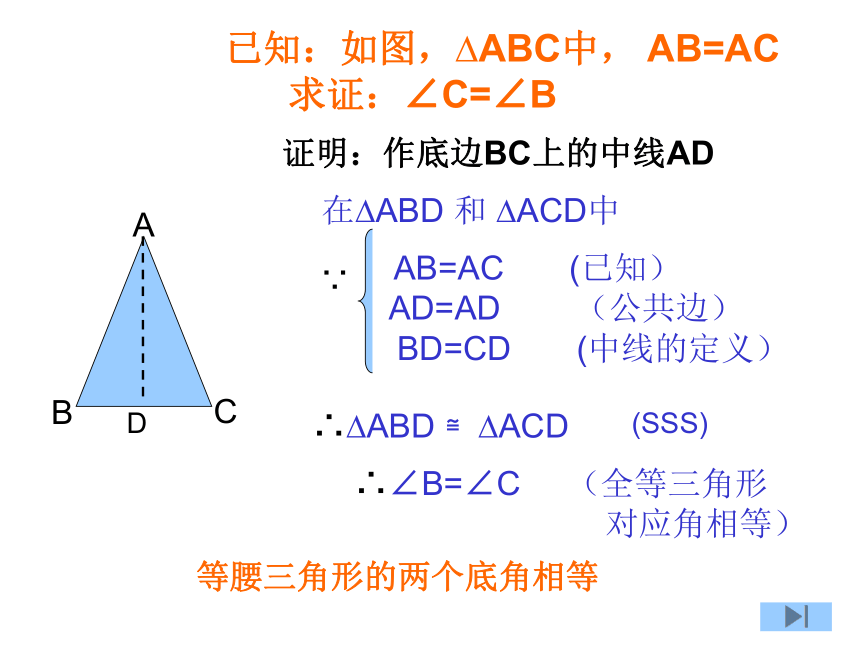
求证: ∠ C =∠ BD“等腰三角形的两个底角相等” 探究新知 已知：如图，?ABC中， AB=AC
求证：∠C=∠BD证明：作底边BC上的中线AD AB=AC (已知）
AD=AD （公共边）
BD=CD (中线的定义）∴?ABD ≌?ACD ∴∠B=∠C （全等三角形
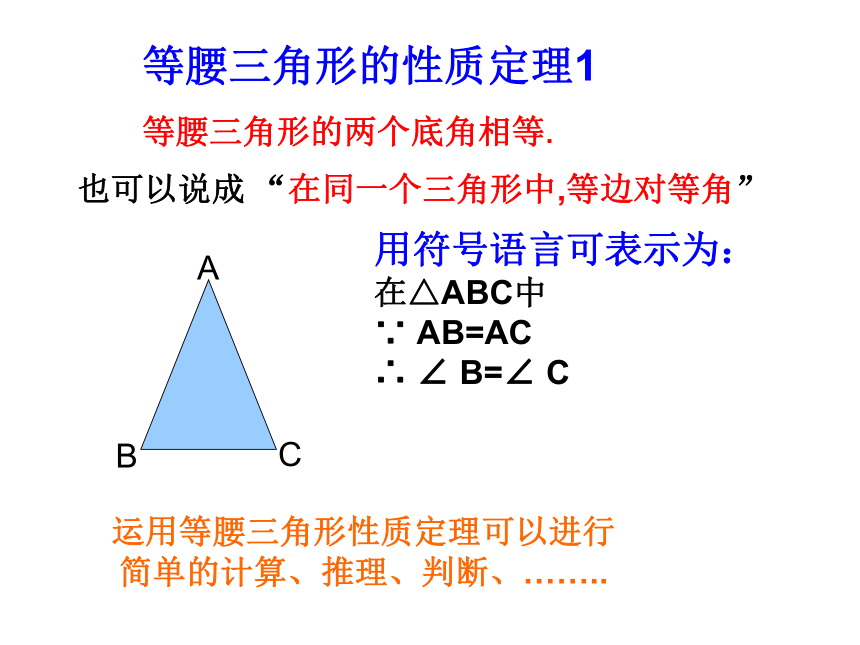
对应角相等）∵(SSS)在?ABD 和 ?ACD中等腰三角形的两个底角相等 等腰三角形的性质定理1 等腰三角形的两个底角相等.也可以说成 “在同一个三角形中,等边对等角”
用符号语言可表示为：
在△ABC中
∵ AB=AC
∴ ∠ B=∠ C
运用等腰三角形性质定理可以进行
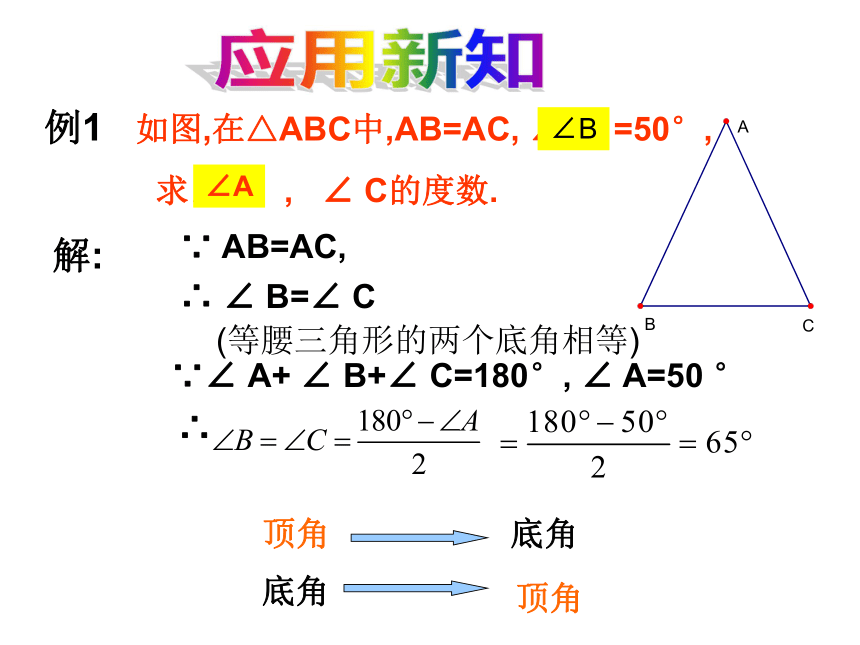
简单的计算、推理、判断、……..应用新知例1 如图,在△ABC中,AB=AC, ∠A =50°,
求∠ B , ∠ C的度数. 解:∵ AB=AC,∴ ∠ B=∠ C(等腰三角形的两个底角相等)∵∠ A+ ∠ B+∠ C=180°, ∠ A=50 °
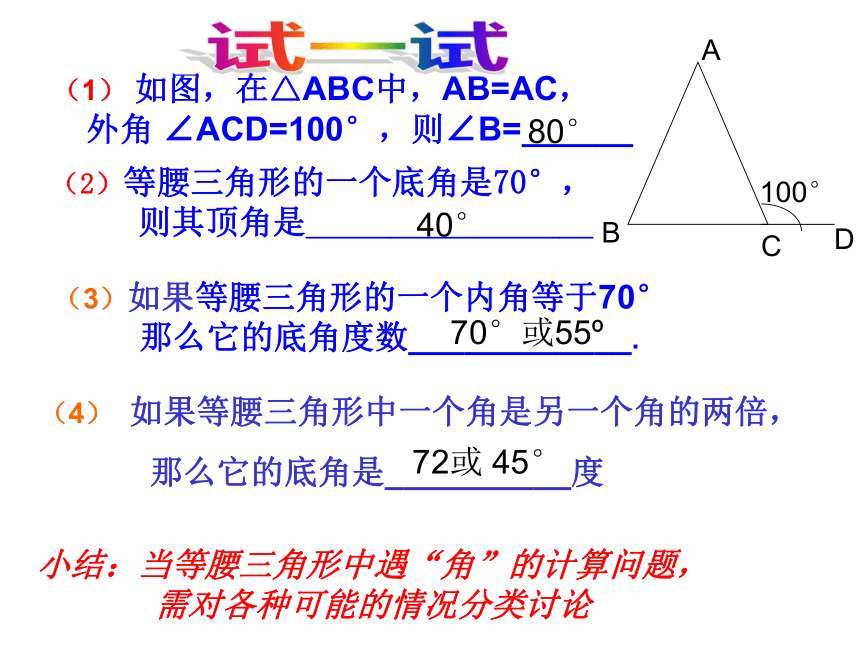
∠B∠A∴底角顶角底角顶角 （2）等腰三角形的一个底角是70°，
则其顶角是_________________
（3）如果等腰三角形的一个内角等于70°
那么它的底角度数____________.
（1） 如图，在△ABC中，AB=AC，
外角 ∠ACD=100°，则∠B=______ （4） 如果等腰三角形中一个角是另一个角的两倍，
那么它的底角是__________度小结：当等腰三角形中遇“角”的计算问题，
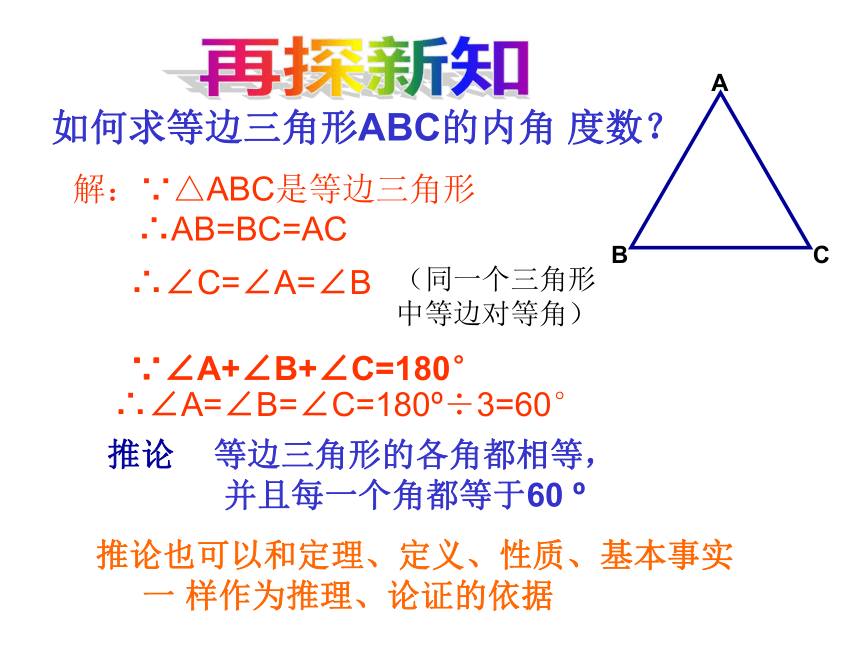
需对各种可能的情况分类讨论80°40°70°或55o72或 45°试一试 推论 等边三角形的各角都相等，
并且每一个角都等于60 o

解：∵△ABC是等边三角形
∴AB=BC=AC
∴∠C=∠A=∠B
（同一个三角形中等边对等角） 推论也可以和定理、定义、性质、基本事实
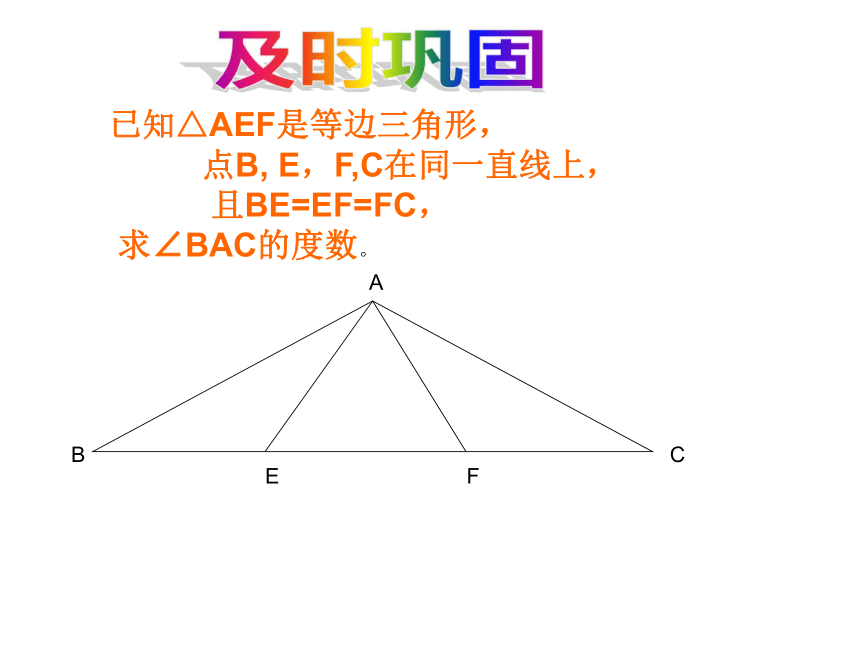
一 样作为推理、论证的依据 ∴∠A=∠B=∠C=180o÷3=60°如何求等边三角形ABC的内角 度数？∵∠A+∠B+∠C=180°再探新知已知△AEF是等边三角形，
点B, E，F,C在同一直线上，
且BE=EF=FC，
求∠BAC的度数。及时巩固“ 等腰三角形
两腰上的中线
_____”
“ 等腰三角形
两腰上的高线 _____ ” “ 等腰三角形
两底角的平分线
相等吗”？
相等 相等再回首已知： 如图 ，在△ABC中，AB＝AC，
BD, CE分别是∠ABC ,∠ACB的平分线。
求证： BD=CE
例2 求证“等腰三角形两底角的平分线相等” 等腰三角形两底角的平分线相等 已知： 如图 ，在△ABC中，AB＝AC，
BD, CE分别是∠ABC ,∠ACB的平分线
求证：BD =CE证明：∵AB=AC
∴∠ABC=∠ACB∵BD, CE分别是∠ABC ,∠ACB的平分线(等边对等角）∴∠ECB=∠DBC∴?BCE≌ ?CBD(ASA)BD=CE(全等三角形对应边相等）∴∠ECB= ∠ACB, ∠DBC= ∠ABC
等腰三角形底角的平分线相等如图，在ΔABC中，AB=AC，P为BC的中点，
点D,E分别在 AB ,AC上，AD=AE
求证：PD=PE.
小结：等腰三角形的性质定理------两个底角相等
（或等边对等角）为两个角相等又增加了一种证明方法
强化新知等腰三角形
的主要特征②从角看-------------①从边看----------③从“三线”看-----------④从整体看---------分类思想 --------在 解决等腰三角形问题中
有着重要 的作用 总结反思两边相等两个底角相等
两腰上的中线相等
两腰上的高线相等
两底角平分线相等是轴对称图形

新知提升（1）已知等腰三角形ABC中，∠A=70°
求 ∠B 的度数 （2）已知△ABC中，AB=AC,且BC=BF=AF
求∠A 的度数13解： ∵BF=AF BF=BC
2∵∠3+ ∠ 2+∠C =180° ∵AB=AC ∴∠1 = ∠A ∠ 2= ∠C ∴ ∠ ABC= ∠C∴α+2α+2α=180°设∠A=α则∠1=α ∴∠2=∠1+ ∠A=2α
∠3=2 α-α=α∴ ∠A=α=36° ∠C=∠ABC=2α
（等边对等角）（等边对等角）FF(1) FA=FB
BC=BF
(2) FA=FB
CB=CF(3) FA=FB
FB=FCF结论：∠A=36°∠A= αα2α2α3αα2α2ααα（3）从等腰三角形纸片的 底角 顶点出发，将其剪成两个
等腰三角形，求原等腰三角形纸片的顶角度数
5α=180°7α=180°顶角提示：等腰三角形，遇到边不确定时要分类讨论问题延伸2：从等腰三角形纸片的顶点出发，
将其剪成两个等腰三角形，
求出此等腰三角形纸片的顶角度数课后再思考：（2）在△ABC中，AB=AC，AB的中垂线与AC所在的直线相交所得的锐角是42°，求∠BEFEF∠B=66°∠B=24°在没有明确等腰三角形的具体形状时，我们要考虑顶角是锐角，直角或钝角的情形。42°42°等腰三角形的顶角的外角等于底角的2倍知识提升二：请你判断 (1) 如 图（1），若AD=AE, 则∠ C= ∠ B （ ） (2) 如图（2），若 AE=EC，则 BE平分 ∠ABC ( )（1）（2）× × “等边对等角”是指“在同一个三角形中，
相等的边所对的角相等”(3)如图（3) 在△ABC中，BC=BA ,则∠A=∠C （ ）√（3）　　将一把等腰三角尺和一个重锤如图１放置，就能检查一根讲台边沿是否水平，你知道为什么吗？ 请你思考等腰三角形一条腰上的高与另一条腰的夹角是50°，
试求出它顶角的度数挑战自己：提示：等腰三角形遇“高线”问题中，要考虑高线在三角形内部和外部两种情形。50°50°顶角140°顶角是40°帮你归纳 1） 等腰三角形一个性质定理：
本节课的我们学习了 2）等腰三角形一个推论：简称：等边对等角 等边三角形的每个内角都等于60° 利用等腰三角形的性质定理
可进行简单的 推理，计算。 4) 分类思想: 在数学解题中起着非常重要的作用3）两底角相等