浙教版九年级数学上册1.4二次函数的应用 同步练习(含解析)
文档属性
| 名称 | 浙教版九年级数学上册1.4二次函数的应用 同步练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 787.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 00:00:00 | ||
图片预览


文档简介
浙教版九年级数学上册同步练习
1.4二次函数的应用
一、选择题(每题3分,共24分)
1.某商场降价销售一批名牌衬衫,已知所获得利润(元)与降价金额(元)之间的关系是,则获利最多为 ( )
A.元 B.元 C.元 D.元
2.某种商品的价格是元,准备进行两次降价.如果每次降价的百分率都是,经过两次降价后的价格(单位:元)随每次降价的百分率的变化而变化,则关于的函数解析式是 ( )
A. B.
C. D.
3.如图,用绳子围成周长为的矩形,记矩形的一边长为,矩形的面积为.当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数表达式为 ( )
A. B.
C. D.
4.向空中发射一枚炮弹,第x秒时的高度为y米,且高度与时间的关系为y=ax2+bx+c(a≠0).若此炮弹在第6秒与第18秒时的高度相等,则在下列时间中炮弹所在高度最高的是 ( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
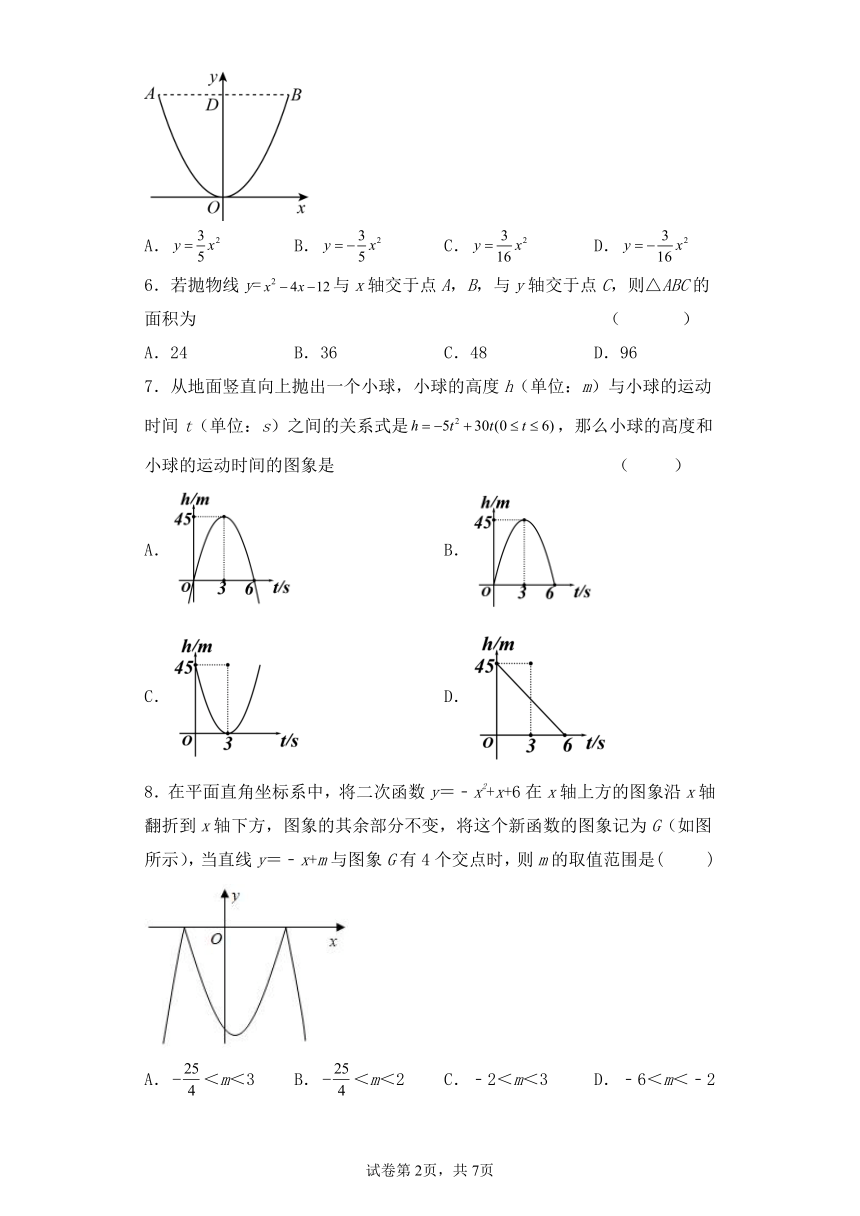
5.如图是一个不倒翁的部分剖面图,可看做一个抛物线,若肚子最大的宽度,,按图示位置建立的平面直角坐标系可知,抛物线表达式为 ( )
A. B. C. D.
6.若抛物线y=与x轴交于点A,B,与y轴交于点C,则△ABC的面积为 ( )
A.24 B.36 C.48 D.96
7.从地面竖直向上抛出一个小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是,那么小球的高度和小球的运动时间的图象是 ( )
A. B.
C. D.
8.在平面直角坐标系中,将二次函数y=﹣x2+x+6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,将这个新函数的图象记为G(如图所示),当直线y=﹣x+m与图象G有4个交点时,则m的取值范围是( )
A.<m<3 B.<m<2 C.﹣2<m<3 D.﹣6<m<﹣2
二、填空题(每题3分,共24分)
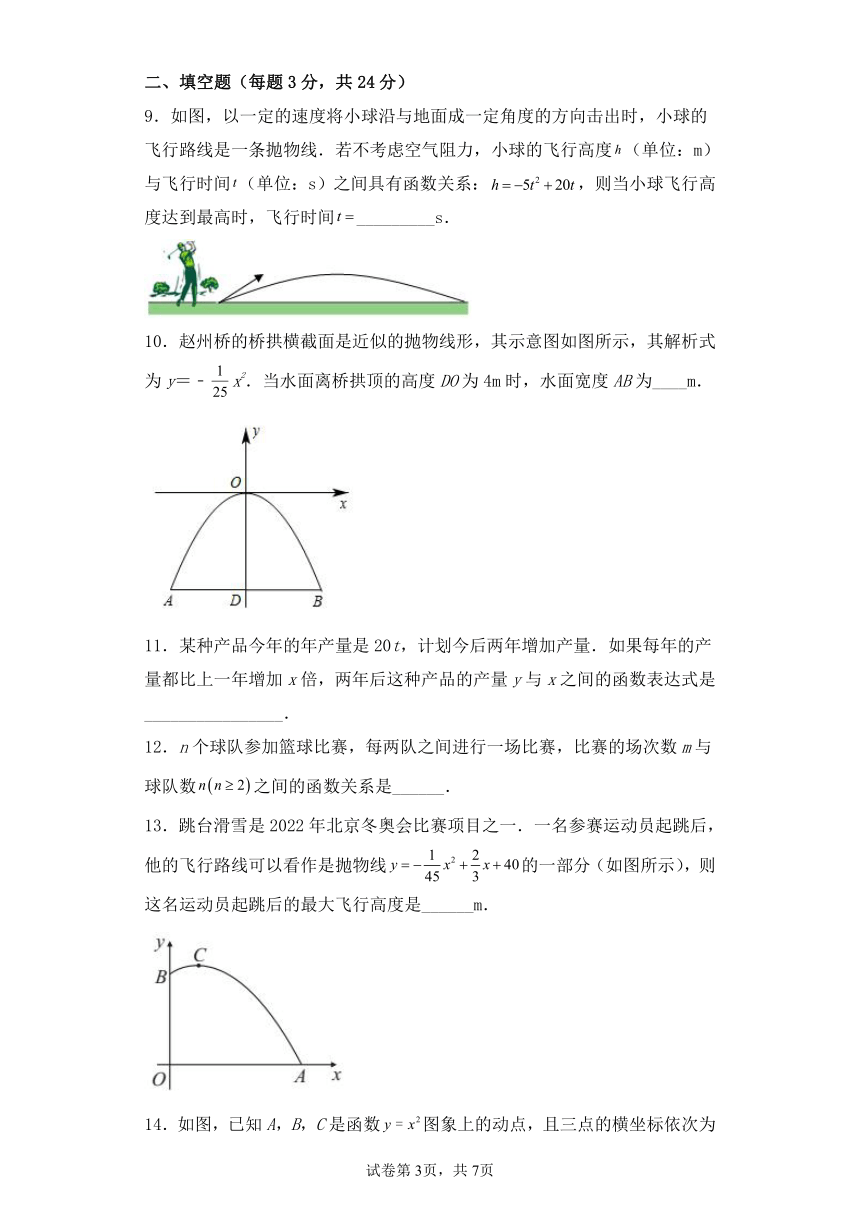
9.如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度(单位:m)与飞行时间(单位:s)之间具有函数关系:,则当小球飞行高度达到最高时,飞行时间_________s.
10.赵州桥的桥拱横截面是近似的抛物线形,其示意图如图所示,其解析式为y=﹣x2.当水面离桥拱顶的高度DO为4m时,水面宽度AB为____m.
11.某种产品今年的年产量是20t,计划今后两年增加产量.如果每年的产量都比上一年增加x倍,两年后这种产品的产量y与x之间的函数表达式是________________.
12.n个球队参加篮球比赛,每两队之间进行一场比赛,比赛的场次数m与球队数之间的函数关系是______.
13.跳台滑雪是2022年北京冬奥会比赛项目之一.一名参赛运动员起跳后,他的飞行路线可以看作是抛物线的一部分(如图所示),则这名运动员起跳后的最大飞行高度是______m.
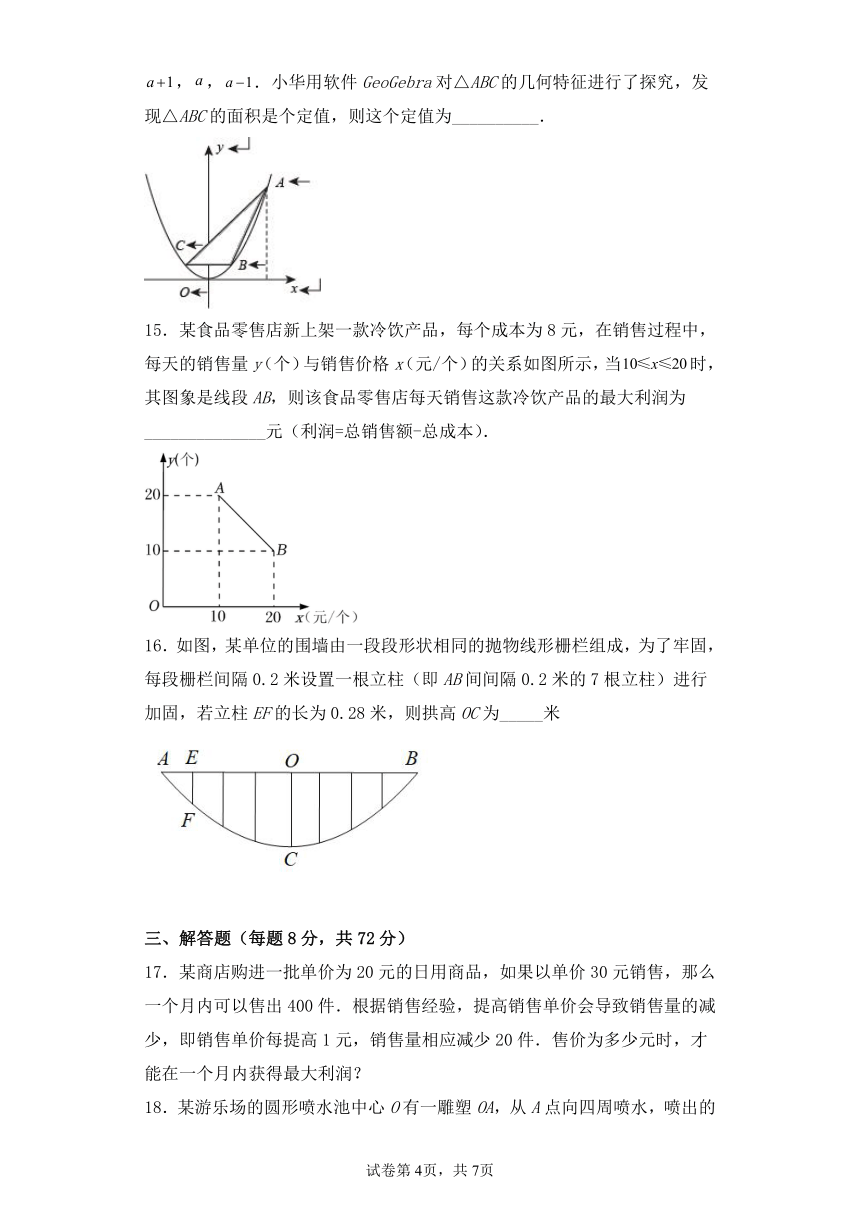
14.如图,已知A,B,C是函数图象上的动点,且三点的横坐标依次为,,.小华用软件GeoGebra对△ABC的几何特征进行了探究,发现△ABC的面积是个定值,则这个定值为__________.
15.某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为______________元(利润=总销售额-总成本).
16.如图,某单位的围墙由一段段形状相同的抛物线形栅栏组成,为了牢固,每段栅栏间隔0.2米设置一根立柱(即AB间间隔0.2米的7根立柱)进行加固,若立柱EF的长为0.28米,则拱高OC为_____米
三、解答题(每题8分,共72分)
17.某商店购进一批单价为20元的日用商品,如果以单价30元销售,那么一个月内可以售出400件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件.售价为多少元时,才能在一个月内获得最大利润?
18.某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同。如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为.
(1)求落水点C、D之间的距离;
(2)若需在OD上离O点10米的E处竖立雕塑EF,,且雕塑的顶部刚好碰到水柱,求雕塑EF的高.
19.如图,在喷水池的中心A处竖直安装一个水管AB.水管的顶端安有一个喷水管、使喷出的抛物线形水柱在与池中心A的水平距离为1m处达到最高点C.高度为3m.水柱落地点D离池中心A处3m.建立适当的平面直角坐标系,解答下列问题.
(1)求水柱所在抛物线的函数解析式;
(2)求水管AB的长.
20.已知一直角三角形两条直角边的和等于8,若其中一直角边为.
(1)写出这个直角三角形的面积关于的函数解析式;
(2)当两条直角边各为多少时这个直角三角形的面积最大?
21.我们不妨约定:纵坐标等于横坐标一半的点叫做“双减点”,例如点(1,),(0,0),(-3,),(m,)……,显然,这样的“双减点”有无数个.根据约定,解答下列问题:
(1)若点(2022,n)是“双减点”,则n= ;
(2)若一次函数y=2x+8的图像上存在“双减点”,试求该图像上“双减点”的坐标;
(3)设二次函数y=x2-2x的图像的双减点为点A,B.(点A在点B左侧),在x轴上找一点P,使得PAB为等腰三角形,求点P的坐标.
22.某网店正在热销一款电子产品,其成本为10元/件,销售中发现,该商品每天的销售量y(件)与销售单价x(元/件)之间存在如图所示的关系:
(1)请求出y与x之间的函数关系式;
(2)该款电子产品的销售单价为多少元时,每天销售利润最大?最大利润是多少元;
23.现要修建一条隧道,其截面为抛物线型,如图所示,线段表示水平的路面,以O为坐标原点,以所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.根据设计要求:,该抛物线的顶点P到的距离为.
(1)求满足设计要求的抛物线的函数表达式;
(2)现需在这一隧道内壁上安装照明灯,如图所示,即在该抛物线上的点A、B处分别安装照明灯.已知点A、B到的距离均为,求点A、B的坐标.
24.跳绳是大家喜爱的一项体育运动,当绳子甩到最高处时,其形状视为抛物线.如图是甲,乙两人将绳子甩到最高处时的示意图,已知两人拿绳子的手离地面的高度都为1m,并且相距4m,现以两人的站立点所在的直线为x轴,过甲拿绳子的手作x轴的垂线为y轴,建立如图所示的平面直角坐标系,且绳子所对应的抛物线解析式为.
(1)求绳子所对应的抛物线解析式(不要求写自变量的取值范围);
(2)身高1.70m的小明,能否站在绳子的正下方,让绳子通过他的头顶?
(3)身高1.64m的小军,站在绳子的下方,设他距离甲拿绳子的手sm,为确保绳子能通过他的头顶,请求出s的取值范围.
25.矩形OABC的顶点A,C分别在x,y轴的正半轴上,点F是边BC上的一个动点(不与点B,C重合),过点F的反比例函数的图象与边AB交于点E(8,m),AB=4.
(1)如图1,若BE=3AE.
①求反比例函数的表达式;
②将矩形OABC折叠,使O点与F点重合,折痕分别与x,y轴交于点H,G,求线段OG的长度.
(2)如图2,连接OF,EF,请用含m的关系式表示OAEF的面积,并求OAEF的面积的最大值.
试卷第1页,共3页
试卷第7页,共7页
参考答案:
1解:对于抛物线,
,
时,有最大值,最大值为,
故选:D.
2.解:根据题意得y=2(1-x)2,
所以y与x之间的函数解析式为y=2(1-x)2.
故选:B.
3.解:由题意得,
2(x+y)=10,
∴x+y=5,
∴y=5﹣x,
∵S=xy
=x(5﹣x)
∴矩形面积满足的函数关系为S=x(5﹣x),
由题意可知自变量的取值范围为,
故选:A.
4.解:此炮弹在第6秒与第18秒时的高度相等,
抛物线的对称轴直线是:,
抛物线开口向下,
时,函数值最大,
即第12秒炮弹所在高度最高,
故选:C.
5.解:∵AB=10cm,OD=15cm,
∴点B的坐标为(5,15),
设抛物线的表达式为y=ax2,
代入(5,15),得:15=a52,
解得:a=,
∴抛物线的表达式为y=x2.
故选:A.
6.解:令y=0,则可得方程=0,
解得:=6,=-2,
故它与x轴的两个交点分别是:(-2,0),(6,0),
当x=0时,y=-12,
故它与y轴的交点是:(0,-12),
∴该三角形的面积为.
故选:C.
7.解:,
令h=0,,
解得:t=0或6,
∴小球的高度和小球的运动时间的图象是开口向下,位于x轴上方抛物线的一段,且顶点坐标为(3,45),
∴B选项图象符合题意.
故选:B
8.解:如图,当y=0时,﹣x2+x+6=0,
解得x1=﹣2,x2=3,
则A(﹣2,0),B(3,0),
将该二次函数在x轴上方的图象沿x轴翻折到x轴下方的部分图象的解析式为y=(x+2)(x﹣3),
即y=x2﹣x﹣6(﹣2≤x≤3),
当直线y=﹣x+m经过点A(﹣2,0)时,2+m=0,解得m=﹣2;
当直线y=﹣x+m与抛物线y=x2﹣x﹣6(﹣2≤x≤3)有唯一公共点时,方程x2﹣x﹣6=﹣x+m有相等的实数解,解得m=﹣6,
所以当直线y=﹣x+m与新图象有4个交点时,m的取值范围为﹣6<m<﹣2.
故选:D.
9.解:∵h=-5t2+20t=-5(t-2)2+20,
且-5<0,
∴当t=2时,h取最大值20,
故答案为:2.
10.解:由题意得,﹣4 =﹣x2,
解得x =±10,
即点A的坐标为(﹣10,﹣4),点B的坐标为(10,﹣4),
这时水面宽度AB为20m,
故答案为:20.
11.解:根据题意得:
故答案为:
12.解:m=n(n-1)=n2-n,
故答案为:m=n(n-1)=n2-n.
13.解:抛物线,
∴抛物线顶点C的坐标为(15,45),
∴这名运动员起跳后的最大飞行高度是45m.
故答案为:45.
14.解:如图,作AD⊥x轴于D,BE⊥x轴于E,CF⊥x轴于F,
∵A,B,C三点的横坐标依次为a+1,a,a-1,
∴AD=(a+1)2=a2+2a+1,BE=a2,CF=(a-1)2=a2-2a+1,
∴S△ABC=S梯形ADFC-S梯形ADEB-S梯形BEFC
=(a2+2a+1+a2-2a+1)×2-(a2+2a+1+a2)×1-(a2+a2-2a+1)×1
=1;
∴△ABC的面积是个定值,这个定值为1.
故答案为:1.
15.解:当时,设,把(10,20),(20,10)代入可得:
,
解得,
∴每天的销售量y(个)与销售价格x(元/个)的函数解析式为,
设该食品零售店每天销售这款冷饮产品的利润为w元,
,
∵1<0,
∴当时,w有最大值为121,
故答案为:121.
16.
解:如图,以点C为坐标系原点,OC所在直线为y轴,建立直角坐标系.
设抛物线的解析式为,
由题意可知:点A的横坐标为-0.8,点F的横坐标为-0.6,
代入,
有,,
点A的纵坐标即为OC的长,
∴0.36a+0.28=0.64a,
解得a=1,
∴抛物线解析式为,
,
故OC的长为:0.64m.
17.解:设销售单价为x元,销售利润为y元,依题意得,单件利润为元,月销量为件,
月销售利润,
整理得,
配方得,
所以时,y取得最大值4500.
故售价为35元时,才能在一个月内获得最大利润,最大利润为4500元.
18. (1)解:当y=0时,,
解得:x1=﹣1(舍去),x2=11,
∴点D的坐标为(11,0),
∴OD=11m.
∵从A点向四周喷水,喷出的水柱为抛物线,且形状相同,
∴OC=OD=11m,
∴CD=OC+OD=22m.
(2)解:∵,,
当x=10时,,
∴点F(10,)
∴雕塑EF的高为米.
19.解:(1)以池中心为原点,竖直安装的水管为y轴,与水管垂直的为x轴建立直角坐标系.
由于在距池中心的水平距离为1m时达到最高,高度为3m,
则设抛物线的解析式为:y=a(x﹣1)2+3,
代入(3,0)求得:a=﹣(x﹣1)2+3.
将a值代入得到抛物线的解析式为:y=﹣(x﹣1)2+3(0≤x≤3);
(2)令x=0,则y==2.25.
故水管AB的长为2.25m.
20. (1)解:=(8-)=4-= -+4
关于的函数解析式为 = -+4;
(2)解:= -+4 =-(-4)+ 8,
∴当=4时,面积最大,
即当两条直角边都为4时,这个直角三角形的面积最大.
21. (1)解∶根据题意得:.
故答案为:1011
(2)解:根据题意得:,
∴,
解得:,
∴,
∴该图像上“双减点”的坐标为;
(3)解:根据题意得:,
∴,解得:,
∴y=0或,
∴点A(0,0),B(,),
设点P(m,0),
当AP=BP时,,
解得:,
此时点;
当AB=AP时,,
解得:,
此时点或;
当时AB=BP时,,
解得:m=5或0(舍去),
此时点P(5,0);
综上所述,点P的坐标为或或或(5,0).
22. (1)解:设y与x的函数关系式为,将(20,100),(25,50)代入y=kx+b,
得 ,
解得 ,
∴y与x的函数关系式为y=﹣10x+300;
(2)解:设该款电子产品每天的销售利润为w元,
由题意得w=(x﹣10) y
=(x﹣10)(﹣10x+300)
=﹣10x2+400x﹣3000
=﹣10(x﹣20)2+1000,
∵﹣10<0,
∴当x=20时,w有最大值,w最大值为1000.
答:该款电子产品销售单价定为20元时,每天销售利润最大,最大销售利润为1000元;
23. (1)依题意,顶点,
设抛物线的函数表达式为,
将代入,得.解之,得.
∴抛物线的函数表达式为.
(2)令,得.
解之,得.
∴.
24. (1)根据题意,抛物线经过点(0,1),(4,1).
∴
解得
∴绳子所对应的抛物线解析式为:y=.
(2)身高1.70m的小明,不能站在绳子的正下方让绳子通过他的头顶.
理由如下:
∵y=,当x=时,
y最大值==.
∴绳子能碰到小明,小明不能站在绳子的正下方让绳子通过他的头顶.
(3)当y=1.64时,=1.64,
即=0.
解得x==.
∴x1=2.4,x2=1.6.
∴.
25. (1)解:①∵BE=3AE,AB=4,
∴AE=1,BE=3,
∴E(8,1),
∴k=8×1=8,
∴反比例函数表达式为y;
②当y=4时,x=2,
∴F(2,4),
∴CF=2,
设OG=x,则CG=4﹣x,FG=x,
由勾股定理得,
,
解得x,
∴OG;
(2)解:∵点E、F在反比例函数的图象上,
∴CF×4=8m,
∴CF=2m,
∴四边形OAEF的面积为8×4
=-+4m+16=﹣+20,
∵0<m<4,
∴当m=2时,四边形OAEF的面积最大为20.
答案第1页,共2页
答案第9页,共10页
1.4二次函数的应用
一、选择题(每题3分,共24分)
1.某商场降价销售一批名牌衬衫,已知所获得利润(元)与降价金额(元)之间的关系是,则获利最多为 ( )
A.元 B.元 C.元 D.元
2.某种商品的价格是元,准备进行两次降价.如果每次降价的百分率都是,经过两次降价后的价格(单位:元)随每次降价的百分率的变化而变化,则关于的函数解析式是 ( )
A. B.
C. D.
3.如图,用绳子围成周长为的矩形,记矩形的一边长为,矩形的面积为.当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数表达式为 ( )
A. B.
C. D.
4.向空中发射一枚炮弹,第x秒时的高度为y米,且高度与时间的关系为y=ax2+bx+c(a≠0).若此炮弹在第6秒与第18秒时的高度相等,则在下列时间中炮弹所在高度最高的是 ( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
5.如图是一个不倒翁的部分剖面图,可看做一个抛物线,若肚子最大的宽度,,按图示位置建立的平面直角坐标系可知,抛物线表达式为 ( )
A. B. C. D.
6.若抛物线y=与x轴交于点A,B,与y轴交于点C,则△ABC的面积为 ( )
A.24 B.36 C.48 D.96
7.从地面竖直向上抛出一个小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是,那么小球的高度和小球的运动时间的图象是 ( )
A. B.
C. D.
8.在平面直角坐标系中,将二次函数y=﹣x2+x+6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,将这个新函数的图象记为G(如图所示),当直线y=﹣x+m与图象G有4个交点时,则m的取值范围是( )
A.<m<3 B.<m<2 C.﹣2<m<3 D.﹣6<m<﹣2
二、填空题(每题3分,共24分)
9.如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度(单位:m)与飞行时间(单位:s)之间具有函数关系:,则当小球飞行高度达到最高时,飞行时间_________s.
10.赵州桥的桥拱横截面是近似的抛物线形,其示意图如图所示,其解析式为y=﹣x2.当水面离桥拱顶的高度DO为4m时,水面宽度AB为____m.
11.某种产品今年的年产量是20t,计划今后两年增加产量.如果每年的产量都比上一年增加x倍,两年后这种产品的产量y与x之间的函数表达式是________________.
12.n个球队参加篮球比赛,每两队之间进行一场比赛,比赛的场次数m与球队数之间的函数关系是______.
13.跳台滑雪是2022年北京冬奥会比赛项目之一.一名参赛运动员起跳后,他的飞行路线可以看作是抛物线的一部分(如图所示),则这名运动员起跳后的最大飞行高度是______m.
14.如图,已知A,B,C是函数图象上的动点,且三点的横坐标依次为,,.小华用软件GeoGebra对△ABC的几何特征进行了探究,发现△ABC的面积是个定值,则这个定值为__________.
15.某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为______________元(利润=总销售额-总成本).
16.如图,某单位的围墙由一段段形状相同的抛物线形栅栏组成,为了牢固,每段栅栏间隔0.2米设置一根立柱(即AB间间隔0.2米的7根立柱)进行加固,若立柱EF的长为0.28米,则拱高OC为_____米
三、解答题(每题8分,共72分)
17.某商店购进一批单价为20元的日用商品,如果以单价30元销售,那么一个月内可以售出400件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件.售价为多少元时,才能在一个月内获得最大利润?
18.某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同。如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为.
(1)求落水点C、D之间的距离;
(2)若需在OD上离O点10米的E处竖立雕塑EF,,且雕塑的顶部刚好碰到水柱,求雕塑EF的高.
19.如图,在喷水池的中心A处竖直安装一个水管AB.水管的顶端安有一个喷水管、使喷出的抛物线形水柱在与池中心A的水平距离为1m处达到最高点C.高度为3m.水柱落地点D离池中心A处3m.建立适当的平面直角坐标系,解答下列问题.
(1)求水柱所在抛物线的函数解析式;
(2)求水管AB的长.
20.已知一直角三角形两条直角边的和等于8,若其中一直角边为.
(1)写出这个直角三角形的面积关于的函数解析式;
(2)当两条直角边各为多少时这个直角三角形的面积最大?
21.我们不妨约定:纵坐标等于横坐标一半的点叫做“双减点”,例如点(1,),(0,0),(-3,),(m,)……,显然,这样的“双减点”有无数个.根据约定,解答下列问题:
(1)若点(2022,n)是“双减点”,则n= ;
(2)若一次函数y=2x+8的图像上存在“双减点”,试求该图像上“双减点”的坐标;
(3)设二次函数y=x2-2x的图像的双减点为点A,B.(点A在点B左侧),在x轴上找一点P,使得PAB为等腰三角形,求点P的坐标.
22.某网店正在热销一款电子产品,其成本为10元/件,销售中发现,该商品每天的销售量y(件)与销售单价x(元/件)之间存在如图所示的关系:
(1)请求出y与x之间的函数关系式;
(2)该款电子产品的销售单价为多少元时,每天销售利润最大?最大利润是多少元;
23.现要修建一条隧道,其截面为抛物线型,如图所示,线段表示水平的路面,以O为坐标原点,以所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.根据设计要求:,该抛物线的顶点P到的距离为.
(1)求满足设计要求的抛物线的函数表达式;
(2)现需在这一隧道内壁上安装照明灯,如图所示,即在该抛物线上的点A、B处分别安装照明灯.已知点A、B到的距离均为,求点A、B的坐标.
24.跳绳是大家喜爱的一项体育运动,当绳子甩到最高处时,其形状视为抛物线.如图是甲,乙两人将绳子甩到最高处时的示意图,已知两人拿绳子的手离地面的高度都为1m,并且相距4m,现以两人的站立点所在的直线为x轴,过甲拿绳子的手作x轴的垂线为y轴,建立如图所示的平面直角坐标系,且绳子所对应的抛物线解析式为.
(1)求绳子所对应的抛物线解析式(不要求写自变量的取值范围);
(2)身高1.70m的小明,能否站在绳子的正下方,让绳子通过他的头顶?
(3)身高1.64m的小军,站在绳子的下方,设他距离甲拿绳子的手sm,为确保绳子能通过他的头顶,请求出s的取值范围.
25.矩形OABC的顶点A,C分别在x,y轴的正半轴上,点F是边BC上的一个动点(不与点B,C重合),过点F的反比例函数的图象与边AB交于点E(8,m),AB=4.
(1)如图1,若BE=3AE.
①求反比例函数的表达式;
②将矩形OABC折叠,使O点与F点重合,折痕分别与x,y轴交于点H,G,求线段OG的长度.
(2)如图2,连接OF,EF,请用含m的关系式表示OAEF的面积,并求OAEF的面积的最大值.
试卷第1页,共3页
试卷第7页,共7页
参考答案:
1解:对于抛物线,
,
时,有最大值,最大值为,
故选:D.
2.解:根据题意得y=2(1-x)2,
所以y与x之间的函数解析式为y=2(1-x)2.
故选:B.
3.解:由题意得,
2(x+y)=10,
∴x+y=5,
∴y=5﹣x,
∵S=xy
=x(5﹣x)
∴矩形面积满足的函数关系为S=x(5﹣x),
由题意可知自变量的取值范围为,
故选:A.
4.解:此炮弹在第6秒与第18秒时的高度相等,
抛物线的对称轴直线是:,
抛物线开口向下,
时,函数值最大,
即第12秒炮弹所在高度最高,
故选:C.
5.解:∵AB=10cm,OD=15cm,
∴点B的坐标为(5,15),
设抛物线的表达式为y=ax2,
代入(5,15),得:15=a52,
解得:a=,
∴抛物线的表达式为y=x2.
故选:A.
6.解:令y=0,则可得方程=0,
解得:=6,=-2,
故它与x轴的两个交点分别是:(-2,0),(6,0),
当x=0时,y=-12,
故它与y轴的交点是:(0,-12),
∴该三角形的面积为.
故选:C.
7.解:,
令h=0,,
解得:t=0或6,
∴小球的高度和小球的运动时间的图象是开口向下,位于x轴上方抛物线的一段,且顶点坐标为(3,45),
∴B选项图象符合题意.
故选:B
8.解:如图,当y=0时,﹣x2+x+6=0,
解得x1=﹣2,x2=3,
则A(﹣2,0),B(3,0),
将该二次函数在x轴上方的图象沿x轴翻折到x轴下方的部分图象的解析式为y=(x+2)(x﹣3),
即y=x2﹣x﹣6(﹣2≤x≤3),
当直线y=﹣x+m经过点A(﹣2,0)时,2+m=0,解得m=﹣2;
当直线y=﹣x+m与抛物线y=x2﹣x﹣6(﹣2≤x≤3)有唯一公共点时,方程x2﹣x﹣6=﹣x+m有相等的实数解,解得m=﹣6,
所以当直线y=﹣x+m与新图象有4个交点时,m的取值范围为﹣6<m<﹣2.
故选:D.
9.解:∵h=-5t2+20t=-5(t-2)2+20,
且-5<0,
∴当t=2时,h取最大值20,
故答案为:2.
10.解:由题意得,﹣4 =﹣x2,
解得x =±10,
即点A的坐标为(﹣10,﹣4),点B的坐标为(10,﹣4),
这时水面宽度AB为20m,
故答案为:20.
11.解:根据题意得:
故答案为:
12.解:m=n(n-1)=n2-n,
故答案为:m=n(n-1)=n2-n.
13.解:抛物线,
∴抛物线顶点C的坐标为(15,45),
∴这名运动员起跳后的最大飞行高度是45m.
故答案为:45.
14.解:如图,作AD⊥x轴于D,BE⊥x轴于E,CF⊥x轴于F,
∵A,B,C三点的横坐标依次为a+1,a,a-1,
∴AD=(a+1)2=a2+2a+1,BE=a2,CF=(a-1)2=a2-2a+1,
∴S△ABC=S梯形ADFC-S梯形ADEB-S梯形BEFC
=(a2+2a+1+a2-2a+1)×2-(a2+2a+1+a2)×1-(a2+a2-2a+1)×1
=1;
∴△ABC的面积是个定值,这个定值为1.
故答案为:1.
15.解:当时,设,把(10,20),(20,10)代入可得:
,
解得,
∴每天的销售量y(个)与销售价格x(元/个)的函数解析式为,
设该食品零售店每天销售这款冷饮产品的利润为w元,
,
∵1<0,
∴当时,w有最大值为121,
故答案为:121.
16.
解:如图,以点C为坐标系原点,OC所在直线为y轴,建立直角坐标系.
设抛物线的解析式为,
由题意可知:点A的横坐标为-0.8,点F的横坐标为-0.6,
代入,
有,,
点A的纵坐标即为OC的长,
∴0.36a+0.28=0.64a,
解得a=1,
∴抛物线解析式为,
,
故OC的长为:0.64m.
17.解:设销售单价为x元,销售利润为y元,依题意得,单件利润为元,月销量为件,
月销售利润,
整理得,
配方得,
所以时,y取得最大值4500.
故售价为35元时,才能在一个月内获得最大利润,最大利润为4500元.
18. (1)解:当y=0时,,
解得:x1=﹣1(舍去),x2=11,
∴点D的坐标为(11,0),
∴OD=11m.
∵从A点向四周喷水,喷出的水柱为抛物线,且形状相同,
∴OC=OD=11m,
∴CD=OC+OD=22m.
(2)解:∵,,
当x=10时,,
∴点F(10,)
∴雕塑EF的高为米.
19.解:(1)以池中心为原点,竖直安装的水管为y轴,与水管垂直的为x轴建立直角坐标系.
由于在距池中心的水平距离为1m时达到最高,高度为3m,
则设抛物线的解析式为:y=a(x﹣1)2+3,
代入(3,0)求得:a=﹣(x﹣1)2+3.
将a值代入得到抛物线的解析式为:y=﹣(x﹣1)2+3(0≤x≤3);
(2)令x=0,则y==2.25.
故水管AB的长为2.25m.
20. (1)解:=(8-)=4-= -+4
关于的函数解析式为 = -+4;
(2)解:= -+4 =-(-4)+ 8,
∴当=4时,面积最大,
即当两条直角边都为4时,这个直角三角形的面积最大.
21. (1)解∶根据题意得:.
故答案为:1011
(2)解:根据题意得:,
∴,
解得:,
∴,
∴该图像上“双减点”的坐标为;
(3)解:根据题意得:,
∴,解得:,
∴y=0或,
∴点A(0,0),B(,),
设点P(m,0),
当AP=BP时,,
解得:,
此时点;
当AB=AP时,,
解得:,
此时点或;
当时AB=BP时,,
解得:m=5或0(舍去),
此时点P(5,0);
综上所述,点P的坐标为或或或(5,0).
22. (1)解:设y与x的函数关系式为,将(20,100),(25,50)代入y=kx+b,
得 ,
解得 ,
∴y与x的函数关系式为y=﹣10x+300;
(2)解:设该款电子产品每天的销售利润为w元,
由题意得w=(x﹣10) y
=(x﹣10)(﹣10x+300)
=﹣10x2+400x﹣3000
=﹣10(x﹣20)2+1000,
∵﹣10<0,
∴当x=20时,w有最大值,w最大值为1000.
答:该款电子产品销售单价定为20元时,每天销售利润最大,最大销售利润为1000元;
23. (1)依题意,顶点,
设抛物线的函数表达式为,
将代入,得.解之,得.
∴抛物线的函数表达式为.
(2)令,得.
解之,得.
∴.
24. (1)根据题意,抛物线经过点(0,1),(4,1).
∴
解得
∴绳子所对应的抛物线解析式为:y=.
(2)身高1.70m的小明,不能站在绳子的正下方让绳子通过他的头顶.
理由如下:
∵y=,当x=时,
y最大值==.
∴绳子能碰到小明,小明不能站在绳子的正下方让绳子通过他的头顶.
(3)当y=1.64时,=1.64,
即=0.
解得x==.
∴x1=2.4,x2=1.6.
∴.
25. (1)解:①∵BE=3AE,AB=4,
∴AE=1,BE=3,
∴E(8,1),
∴k=8×1=8,
∴反比例函数表达式为y;
②当y=4时,x=2,
∴F(2,4),
∴CF=2,
设OG=x,则CG=4﹣x,FG=x,
由勾股定理得,
,
解得x,
∴OG;
(2)解:∵点E、F在反比例函数的图象上,
∴CF×4=8m,
∴CF=2m,
∴四边形OAEF的面积为8×4
=-+4m+16=﹣+20,
∵0<m<4,
∴当m=2时,四边形OAEF的面积最大为20.
答案第1页,共2页
答案第9页,共10页
同课章节目录
