1.3 证明（2）课件

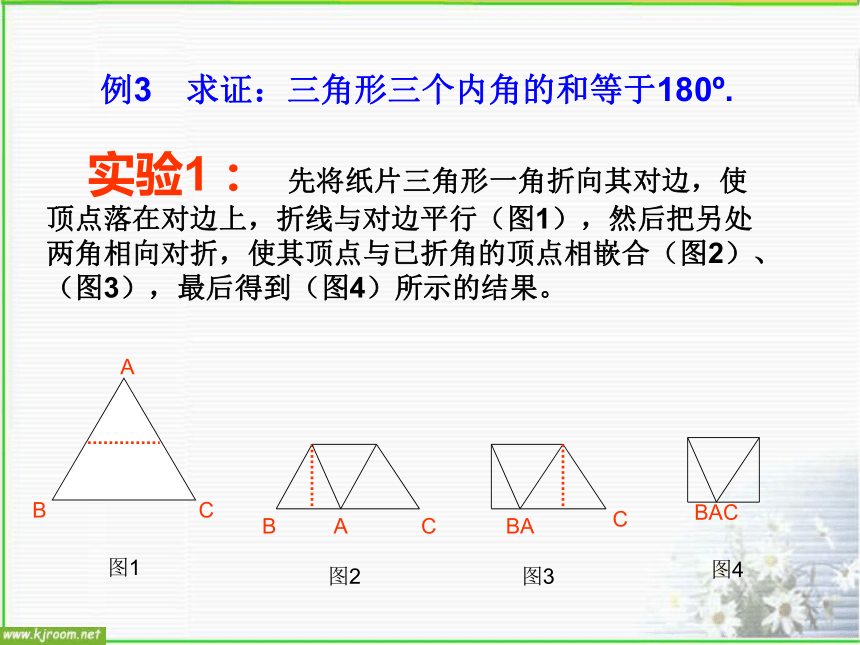
课件16张PPT。泰顺六中 翁怀新2013年9月12日1.3 证明（2）胜者的“钥匙”证明命题的一般步骤:(1)根据题意,画出图形；(2)分清命题的条件和结论，结合图形，在“已知”中写出条件，在“求证”中写出结论；(3)在“证明”中写出推理过程.　　依据思路,运用数学符号和数学语言条理清晰地写出证明过程；检查表达过程是否正确、完善. 实验1： 先将纸片三角形一角折向其对边，使顶点落在对边上，折线与对边平行（图1），然后把另处两角相向对折，使其顶点与已折角的顶点相嵌合（图2）、（图3），最后得到（图4）所示的结果。
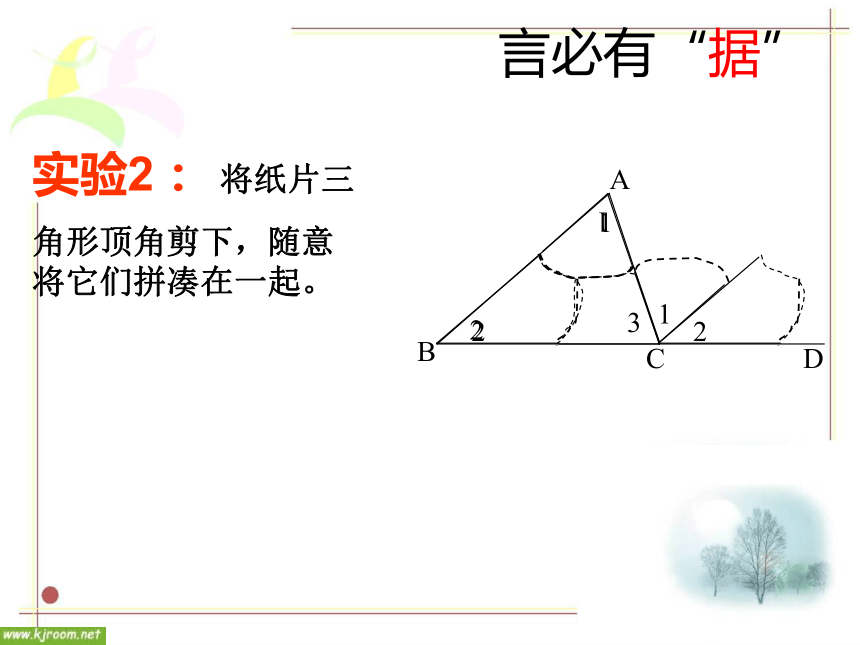
例3　求证：三角形三个内角的和等于180o.言必有“据”12ABD3C实验2： 将纸片三
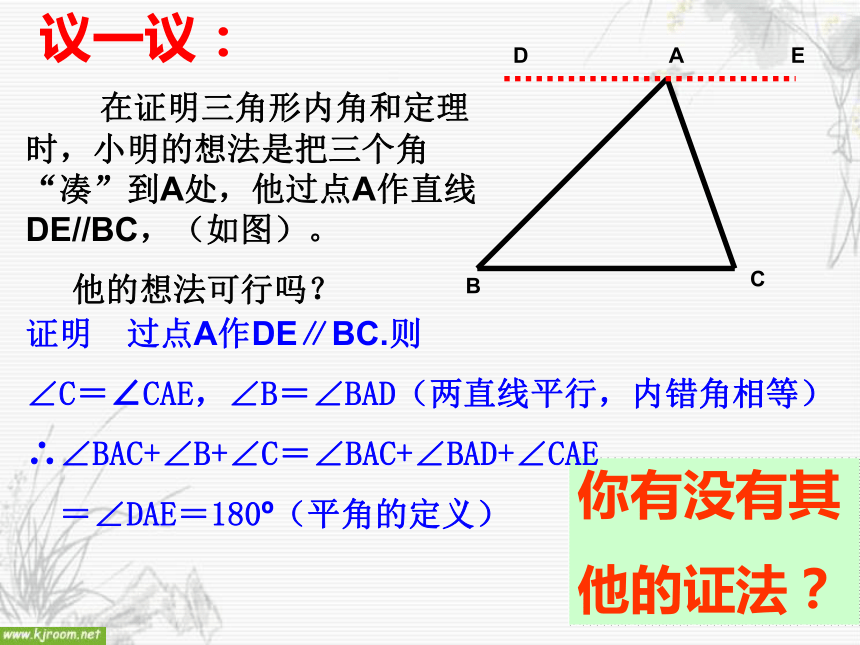
角形顶角剪下，随意将它们拼凑在一起。议一议： 在证明三角形内角和定理时，小明的想法是把三个角“凑”到A处，他过点A作直线DE//BC，（如图）。
他的想法可行吗？你有没有其
他的证法？证明　过点A作DE∥BC.则
∠C＝∠CAE，∠B＝∠BAD（两直线平行，内错角相等）
∴∠BAC+∠B+∠C＝∠BAC+∠BAD+∠CAE
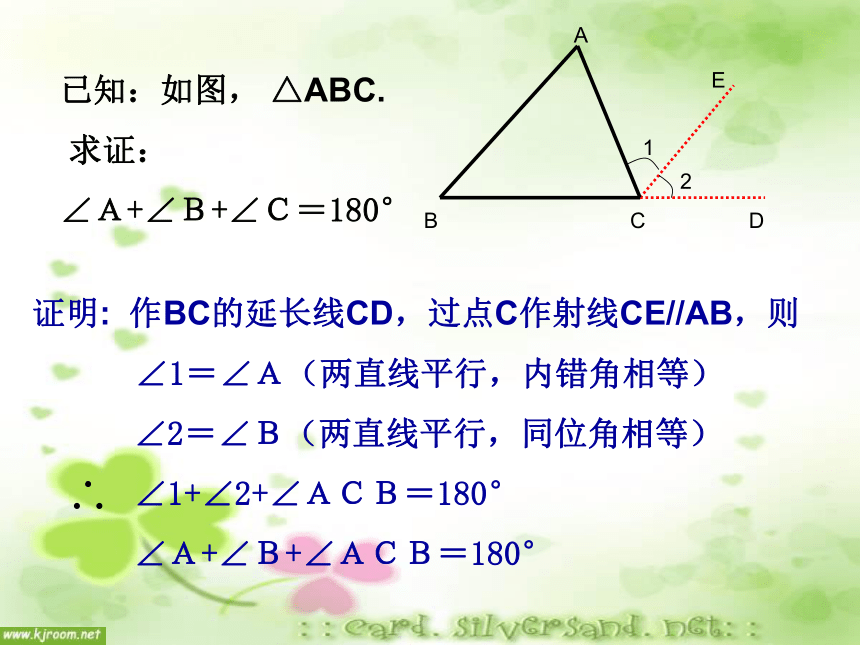
　＝∠DAE＝180o（平角的定义）证明: 作BC的延长线CD，过点C作射线CE//AB，则
∠1＝∠Ａ（两直线平行，内错角相等）
∠2＝∠Ｂ（两直线平行，同位角相等）
∠1+∠2+∠ＡＣＢ＝180°
∠Ａ+∠Ｂ+∠ＡＣＢ＝180°三角形内角和定理三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.这里的结论,以后可以直接运用. 关于辅助线：辅助线是为了证明需要在原图上添画的线.（辅助线通常画成虚线）
它的作用是把分散的条件集中，把隐含的条件显现出来，起到牵线搭桥的作用.
添加辅助线，可构造新图形，形成新关系，找到联系已知与未知的桥梁，把问题转化，但辅助线的添法没有一定的规律，要根据需要而定,平时做题时要注意总结.(1) 添加辅助线在许多几何证明题中是关键一步(2) 添平行线可以构造许多相等的角ZUOYIZUO课内练习1、p19页1题例4已知：如图，∠B+∠D=∠BCD,
求证： AB∥DE分析 如右图所示，延长BC，交DE于
点F，根据平行线的判定定理，只要
证明∠B=∠CFD或∠B+∠BFE=1800 ，
就能证明AB∥DE。BEFCDA证明：如右图延长BC，交DE于F,∵∠B+∠D= ∠B CD(已知)又∵∠BCD是△DCF 的一个外角∴　∠BCD=∠D+∠ CFD
(三角形的一个外角等于和它不相邻的两个内角的和）∴ 　∠B+ ∠D= ∠D+ ∠ CFD∴ ∠B= ∠ CFD 即 AB∥DE（内错角相等， 两直线平行）ZUOYIZUO课内练习2、p19页2题本堂课我们学到了什么新知识？本堂课我们学到；
1、进一步学习证明的思考方法；
2、进一步学习证明的方法和表述体验添加辅助线在证明中的作用。小结；知识的升华1、作业本P3-4
2、课时特训P10-12
祝你成功！再见！