1.5三角形全等的判定（1）

课件27张PPT。教材分析 1、教学内容：浙教版八年级上册第一章第1。5节内容，课本25页到28页。
2、教材的地位和作用： 本节内容作为“探索三角形全等的条件”的第一课时，通过探究活动，使学生在实践中学习创造性地思维，是培养学生自主学习合作交流的好素材。且通过观察多媒体的动画演示，大力地培养了学生的空间观念，并在探索过程中，发展了学生有条理的思考能力。在应用“边边边”定理和稳定性性质中，发展了推理能力和应用意识，故包含了丰富的数学思想，这是本节课的精辟所在。
教学目标（1）知识目标：
1、探索并掌握两个三角形全等的条件：有三边对应相等的两个
三角形全等（SSS）。
2、了解三角形的稳定性及其应用。
3、会运用“SSS”判定两个三角形全等。
4、掌握角平分线的尺规作图。（2）能力目标：
让学生学会有条理地思考、分析、解决问题的能力，培养推理、应用能力和空间想象能力。 （3）情感目标：
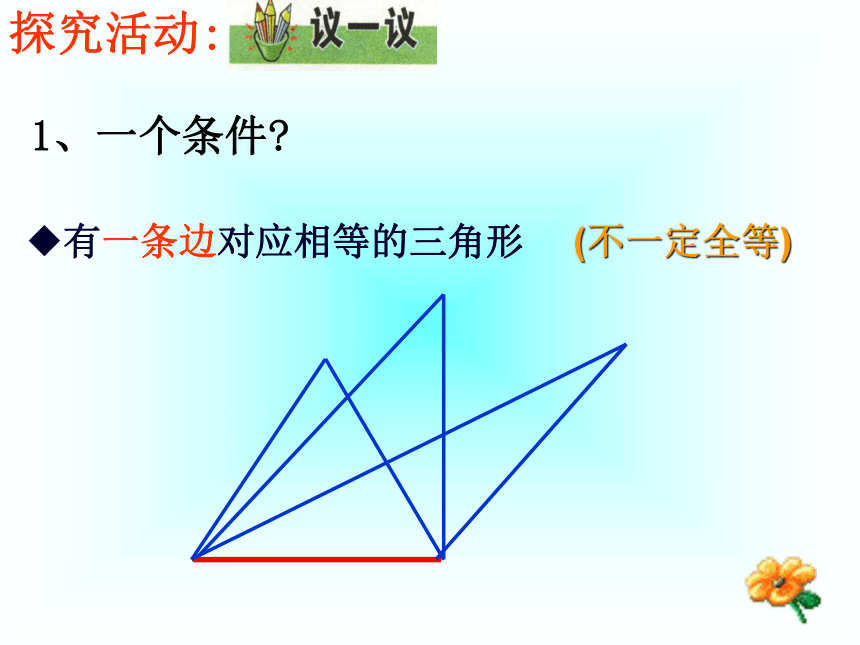
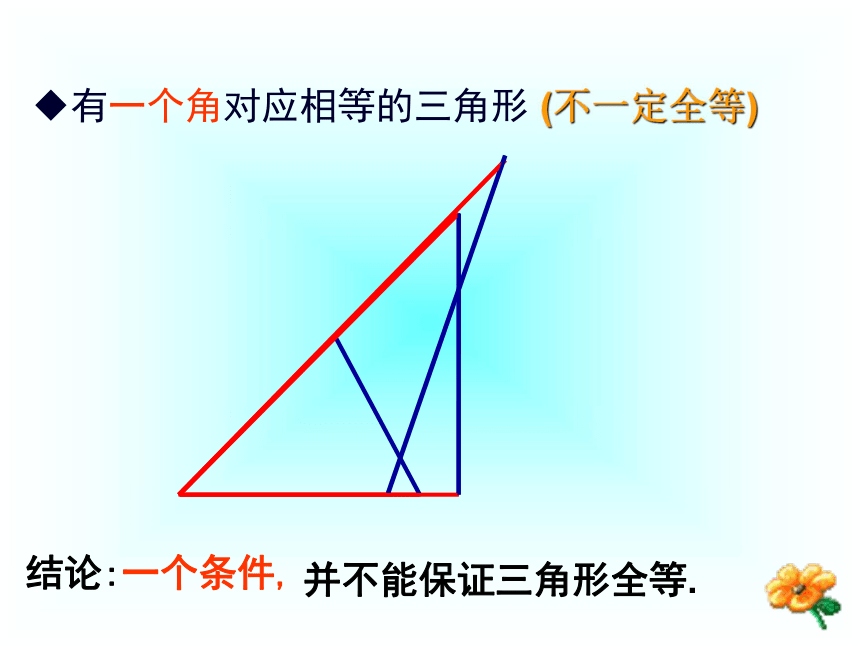
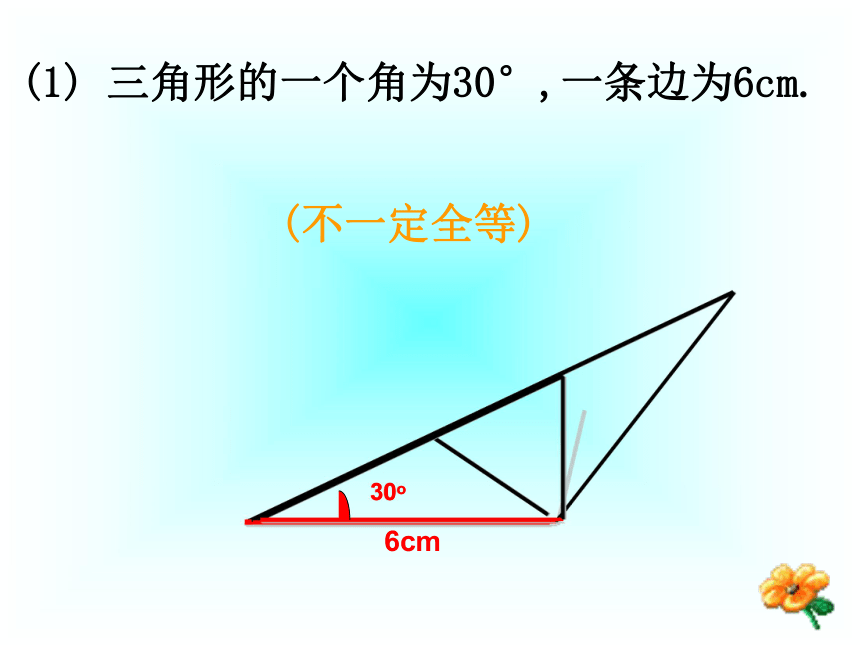
让学生学会大胆探索、善于归纳、应用、培养学生个性，优化数学思维品质。教学重点和难点教学重点：两个三角形全等的条件：有三边对应相等的两个三角形全等。 “尺规作图”是学生初次遇到的数学问题，它不仅对作图工具了限制，而且还要求学生写作法，是本节教学的难点。教学难点：泰顺六中 翁怀新2013年9月16日1.5 三角形全等的判定(1)情境问题: 小明家的衣橱上镶有两块全等的三角形玻璃装饰物,其中一块被打碎了,妈妈让小明到玻璃店配一块回来.同学们,发挥你的想象力,你觉得小明这时该测量哪些数据呢?数据能尽可能少吗？ 1、一个条件?有一条边对应相等的三角形(不一定全等)探究活动:有一个角对应相等的三角形结论:一个条件,并不能保证三角形全等.(不一定全等)按照下面给出的两个条件画出三角形,并与其他同学的比一比!(1)三角形的一个角为 30°,一条边为6cm ;(2)三角形的两条边分别是 4cm 和 6cm ;(3)三角形的两个角分别是 30°和 60°. 2、两个条件?(不一定全等)(1) 三角形的一个角为30°,一条边为6cm.(2)三角形的两条边分别是：4cm，6cm.(不一定全等)(3)三角形的两个角分别是：30°，60°.结论：有两个条件对应相等也不能保证三角形全等.(不一定全等) 3、三个条件?（1）已知三角形的三个角分别为30°,60°,90°. 三个内角对应相等的三角形不一定全等。结论:(2)已知三角形三条边分别是 4cm，5cm，7cm，画出这个
三角形，把所画的三角形分别剪下来，并与同伴比一比，
发现什么？三边对应相等的两个三角形全等，探究新知(★依次点击即可)三角形全等的条件(或判定）: 一般地,有三边对应相等的两个三角形全等.
可以简写成 “边边边” 或“ SSS ” S ——边AB=A’B’BC=B’C’AC=A’C’（SSS）数学表达式：在△ABC和△A’B’C’中（SSS）例1:如图，在四边形ABCD中,AB=CD，AD=CB，
则∠A=∠C.请说明理由。AB=CD （已知）AD=CB （已知）BD=DB（公共边）∴ ∠A= ∠C
(全等三角形的对应角相等)例题练一练:SSS BCCB
△DCBBF=CD 或 BD=CF(课内练习P21 T2.)取出课前自制长度适当的木条，把它们分别做成三角形和四边形
框架，并拉动它们。你发现什么？ 三角形的大小和形状是固定不变的，而四边形的形状会改变。做一做:三角形的稳定性：当三角形的三条边长确定时，三角形的形状、大小完全被确定，
这个性质叫三角形的稳定性。三角形的稳定性在生活中的应用：LITIJIANXI 例2 已知∠BAC（如图），用直尺和圆规作∠BAC的平分线AD，并说出该作法正确的理由。FED（1）以点A为圆心，适当长为半径作圆弧，与角的两边分别交于E、F两点。 （2）分别以E、F为圆心，大于二分之一EF长为半径作圆弧，两条弧交于点D。（3）过点A、D作射线AD。（4）AD就是所求的角平分线。KENEILIANXI 如图，点B、E、C、F在同一条直线上，且AB=DE，AC=DF，BE=CF。请将下面说明△ABC≌△DEF的过程和理由补充完整。∴ △ABD≌△CBD （ ）在△ABC和△DEF中AB= （ ）∵ BE=CF （ ）∴ BE+EC=CF+EC，即BC=EF =DF（ ）BC= （ ）∵解已知已知DEAC已知EF已证SSS知识回顾1. 已知三边长画三角形的方法.2. 三角形全等条件一.3. 三角形的稳定性.4. 角平分线的尺规作图法.请同学们谈谈本节课的收获与体会:本节课你学到了什么？
发现了什么？
有什么收获？
还存在什么没有解决的问题？ 课后作业:1、课本P21-22课后作业题2、作业本§1.5再　见！