浙教版(2019)高中信息技术必修1 迭代 课件(14张PPT)
文档属性
| 名称 | 浙教版(2019)高中信息技术必修1 迭代 课件(14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-09-14 08:33:21 | ||
图片预览






文档简介
(共14张PPT)
第五章 迭代
用Python程序编程实现求s=1+2+3+…+n的代码。
n=int(input(“请输入一个正整数:”))
s=0
for i in range(1,n+1):
s=s+i
print(s)
迭代实例:
迭代的科学概念:
重复反馈过程的活动,其目的通常是是为了使结果符合目标需求。每一次对过程的重复被称为一次迭代,而每一次迭代得到的结果会被用来作为下一次迭代的初始值。
计算机解决问题时,也经常采用这种迭代的方式,即迭代算法。它利用计算机运算速度快、适合做重复性操作的特点,让计算机重复执行一组指令(或一些步骤),这组指令(或这些步骤)每执行一次时,都会将变量从原值递推出一个新值。
迭代的概念:
利用迭代算法处理问题,需要考虑以下三个方面:
①确定迭代变量。
在能够用迭代算法处理的问题中,至少具有一个直接或间接地不断由旧值递推出新值的变量,这个变量就是迭代变量。
②建立迭代关系式(数值关系)。
所谓迭代关系式,指如何从变量的前一个值推出其下一个值的公式(或关系)。
③控制迭代过程(结束条件)。
迭代过程在经过若干次重复执行以后要能结束,因此,要设定迭代结束的条件。
迭代的算法:
n=int(input(“请输入一个正整数:”))
s=0
for i in range(1,n+1):
s=s+i
print(s)
迭代实例:
迭代变量?数值关系?迭代过程?
迭代实例:斐波那契数列、黄金分割数列、兔子数列
黄金分割数列:第10个数字是什么?
f1 f2 f1+f2
1 1 2
1 2 3
2 3 5
3 5 8
5 8 13
8 13 21
13 21 34
①确定迭代变量。②建立迭代关系。③控制迭代(结束)过程。
f1,f2=1,1
f3=f1+f2
程序实现:
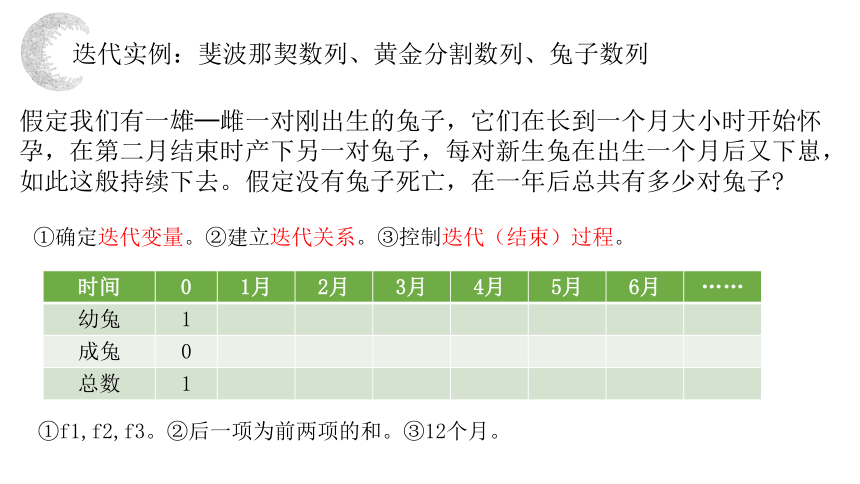
迭代实例:斐波那契数列、黄金分割数列、兔子数列
假定我们有一雄─雌一对刚出生的兔子,它们在长到一个月大小时开始怀孕,在第二月结束时产下另一对兔子,每对新生兔在出生一个月后又下崽,如此这般持续下去。假定没有兔子死亡,在一年后总共有多少对兔子
①确定迭代变量。②建立迭代关系。③控制迭代(结束)过程。
时间 0 1月 2月 3月 4月 5月 6月 ……
幼兔 1
成兔 0
总数 1
①f1,f2,f3。②后一项为前两项的和。③12个月。
迭代实例:斐波那契数列、黄金分割数列、兔子数列
假定一对大兔子每月能生一对小兔子,且每对新生的小兔子经过一个月可以长成一对大兔子,具备繁殖能力,如果不发生死亡,且每次均生下一雌一雄。问一年后共有多少对兔子?
①确定迭代变量。②建立迭代(数值)关系式。③控制迭代(结束)过程。
时间 0 1月 2月 3月 4月 5月 6月 ……
幼兔 1 0 1 1 2 3 5
成兔 0 1 1 2 3 5 8
总数 1 1 2 3 5 8 13
迭代实例:斐波那契数列、黄金分割数列、兔子数列
时间 0 1月 2月 3月 4月 5月 6月 ……
幼兔 1 0 1 1 2 3 5
成兔 0 1 1 2 3 5 8
总数 1 1 2 3 5 8 13
程序实现:
f1=1
f2=2
for i in range(3,13):
f3=f1+f2
f1=f2
f2=f3
print(f3)
f1=1
f2=2
for i in range(3,13):
f1,f2,=f2,f1+f2
print(f2)
辗转相除法求两个数的最大公约数的步骤如下:
先用小的一个数除大的一个数,得第一个余数;
再用第一个余数除小的一个数,得第二个余数;
又用第二个余数除第一个余数,得第三个余数;
这样逐次用后一个数去除前一个余数,直到余数是0为止.
那么,最后一个除数就是所求的最大公约数(如果最后的除数是1,那么原来的两个数是互质数).
例如求1515和600的最大公约数:
第一次:用600除1515,商2余315;第二次:用315除600,商1余285;
第三次:用285除315,商1余30;第四次:用30除285,商9余15;
第五次:用15除30,商2余0.
1515和600的最大公约数是15.
典型应用:辗转相除法、欧几里得算法
典型应用:欧几里得算法
欧几里得算法又称辗转相除法,用于计算两个整数m,n的最大公约数。
基于定理:
gcd(m,n)=gcd(n,m%n)
即:整数m,n的最大公约数等于n和m除以n的余数的最大公约数。
欧几里得算法在执行时,也是一个反复迭代的过程,直到余数等于0为止。
Python代码实现如下:
def gcd(m,n):
while n!=0:
temp=n
n=m%n
m=temp
return m
m,n是迭代变量,迭代关系式n m和
m%n n,由旧值推出新值,然后循环
执行,直到余数为0,结束迭代。
例:采用迭代算法求a的平方根。
基本思路:先估测一个近似值x,然后不断令x等于x和的平均数(迭代公式为:xn+1=(xn+)(n>=0)),经过若干次迭代后,x的值将逐渐逼近a的平方根。
以求2的平方根为例,可估测一个近似值(如x0=1)作为初值,设定
前后两次求出的x的差的绝对值小于10-5。
迭代次数 xn xn+1 |xn+1-xn|
1 1 1.5 0.5
2 1.5 1.416667 0.083333
3 1.416667 1.414216 0.002451
4 1.414216 1.414214 0.000002
相应的程序及测试结果如下所示:
a=int(input(“请输入一个需要求其平方根的数:”))
x=a/2
while((abs(x+a/x)/2-x))>0.00001):
x=(x+a/x)/2
print(a,“的平方根约为”,round((x+a/x)/2,6))
请输入一个需要求其平方根的数:2
2的平方根约为1.414214
在用迭代法求2的平方根的例子中,若将迭代变量
X的初值换为其他数值,对运行结果和迭代次数是否有影响?
若把x的值设置为0或者其他负值,则将得到错误的迭代结果。一般
情况下,应当把x的初值设置为接近于正确解的估值,这样可以得到
正确的结果,同时迭代次数也会减少。一般而言,应当注意求根公式
的三个问题:一是问题本身应有解;二是选择的初值应接近解的估值,
以减少迭代次数;三是迭代公式应该是正确的。
第五章 迭代
用Python程序编程实现求s=1+2+3+…+n的代码。
n=int(input(“请输入一个正整数:”))
s=0
for i in range(1,n+1):
s=s+i
print(s)
迭代实例:
迭代的科学概念:
重复反馈过程的活动,其目的通常是是为了使结果符合目标需求。每一次对过程的重复被称为一次迭代,而每一次迭代得到的结果会被用来作为下一次迭代的初始值。
计算机解决问题时,也经常采用这种迭代的方式,即迭代算法。它利用计算机运算速度快、适合做重复性操作的特点,让计算机重复执行一组指令(或一些步骤),这组指令(或这些步骤)每执行一次时,都会将变量从原值递推出一个新值。
迭代的概念:
利用迭代算法处理问题,需要考虑以下三个方面:
①确定迭代变量。
在能够用迭代算法处理的问题中,至少具有一个直接或间接地不断由旧值递推出新值的变量,这个变量就是迭代变量。
②建立迭代关系式(数值关系)。
所谓迭代关系式,指如何从变量的前一个值推出其下一个值的公式(或关系)。
③控制迭代过程(结束条件)。
迭代过程在经过若干次重复执行以后要能结束,因此,要设定迭代结束的条件。
迭代的算法:
n=int(input(“请输入一个正整数:”))
s=0
for i in range(1,n+1):
s=s+i
print(s)
迭代实例:
迭代变量?数值关系?迭代过程?
迭代实例:斐波那契数列、黄金分割数列、兔子数列
黄金分割数列:第10个数字是什么?
f1 f2 f1+f2
1 1 2
1 2 3
2 3 5
3 5 8
5 8 13
8 13 21
13 21 34
①确定迭代变量。②建立迭代关系。③控制迭代(结束)过程。
f1,f2=1,1
f3=f1+f2
程序实现:
迭代实例:斐波那契数列、黄金分割数列、兔子数列
假定我们有一雄─雌一对刚出生的兔子,它们在长到一个月大小时开始怀孕,在第二月结束时产下另一对兔子,每对新生兔在出生一个月后又下崽,如此这般持续下去。假定没有兔子死亡,在一年后总共有多少对兔子
①确定迭代变量。②建立迭代关系。③控制迭代(结束)过程。
时间 0 1月 2月 3月 4月 5月 6月 ……
幼兔 1
成兔 0
总数 1
①f1,f2,f3。②后一项为前两项的和。③12个月。
迭代实例:斐波那契数列、黄金分割数列、兔子数列
假定一对大兔子每月能生一对小兔子,且每对新生的小兔子经过一个月可以长成一对大兔子,具备繁殖能力,如果不发生死亡,且每次均生下一雌一雄。问一年后共有多少对兔子?
①确定迭代变量。②建立迭代(数值)关系式。③控制迭代(结束)过程。
时间 0 1月 2月 3月 4月 5月 6月 ……
幼兔 1 0 1 1 2 3 5
成兔 0 1 1 2 3 5 8
总数 1 1 2 3 5 8 13
迭代实例:斐波那契数列、黄金分割数列、兔子数列
时间 0 1月 2月 3月 4月 5月 6月 ……
幼兔 1 0 1 1 2 3 5
成兔 0 1 1 2 3 5 8
总数 1 1 2 3 5 8 13
程序实现:
f1=1
f2=2
for i in range(3,13):
f3=f1+f2
f1=f2
f2=f3
print(f3)
f1=1
f2=2
for i in range(3,13):
f1,f2,=f2,f1+f2
print(f2)
辗转相除法求两个数的最大公约数的步骤如下:
先用小的一个数除大的一个数,得第一个余数;
再用第一个余数除小的一个数,得第二个余数;
又用第二个余数除第一个余数,得第三个余数;
这样逐次用后一个数去除前一个余数,直到余数是0为止.
那么,最后一个除数就是所求的最大公约数(如果最后的除数是1,那么原来的两个数是互质数).
例如求1515和600的最大公约数:
第一次:用600除1515,商2余315;第二次:用315除600,商1余285;
第三次:用285除315,商1余30;第四次:用30除285,商9余15;
第五次:用15除30,商2余0.
1515和600的最大公约数是15.
典型应用:辗转相除法、欧几里得算法
典型应用:欧几里得算法
欧几里得算法又称辗转相除法,用于计算两个整数m,n的最大公约数。
基于定理:
gcd(m,n)=gcd(n,m%n)
即:整数m,n的最大公约数等于n和m除以n的余数的最大公约数。
欧几里得算法在执行时,也是一个反复迭代的过程,直到余数等于0为止。
Python代码实现如下:
def gcd(m,n):
while n!=0:
temp=n
n=m%n
m=temp
return m
m,n是迭代变量,迭代关系式n m和
m%n n,由旧值推出新值,然后循环
执行,直到余数为0,结束迭代。
例:采用迭代算法求a的平方根。
基本思路:先估测一个近似值x,然后不断令x等于x和的平均数(迭代公式为:xn+1=(xn+)(n>=0)),经过若干次迭代后,x的值将逐渐逼近a的平方根。
以求2的平方根为例,可估测一个近似值(如x0=1)作为初值,设定
前后两次求出的x的差的绝对值小于10-5。
迭代次数 xn xn+1 |xn+1-xn|
1 1 1.5 0.5
2 1.5 1.416667 0.083333
3 1.416667 1.414216 0.002451
4 1.414216 1.414214 0.000002
相应的程序及测试结果如下所示:
a=int(input(“请输入一个需要求其平方根的数:”))
x=a/2
while((abs(x+a/x)/2-x))>0.00001):
x=(x+a/x)/2
print(a,“的平方根约为”,round((x+a/x)/2,6))
请输入一个需要求其平方根的数:2
2的平方根约为1.414214
在用迭代法求2的平方根的例子中,若将迭代变量
X的初值换为其他数值,对运行结果和迭代次数是否有影响?
若把x的值设置为0或者其他负值,则将得到错误的迭代结果。一般
情况下,应当把x的初值设置为接近于正确解的估值,这样可以得到
正确的结果,同时迭代次数也会减少。一般而言,应当注意求根公式
的三个问题:一是问题本身应有解;二是选择的初值应接近解的估值,
以减少迭代次数;三是迭代公式应该是正确的。
