2.3等腰三角形的性质定理2

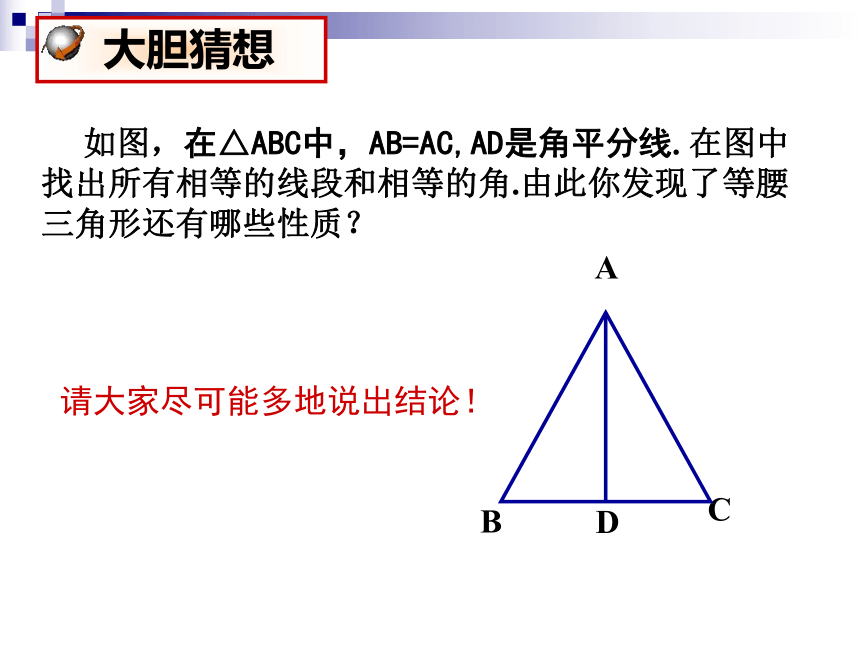
课件14张PPT。2.3等腰三角形的性质定理2 如图，在△ABC中，AB=AC,AD是角平分线. 在图中找出所有相等的线段和相等的角.由此你发现了等腰三角形还有哪些性质？ 大胆猜想请大家尽可能多地说出结论！等腰三角形的顶角平分线、底边上的中线和高线互相重合,简称等腰三角形三线合一等腰三角形的性质定理2等腰三角形的顶角平分线就是底边上的中线和高线；你怎么理解这个定理？
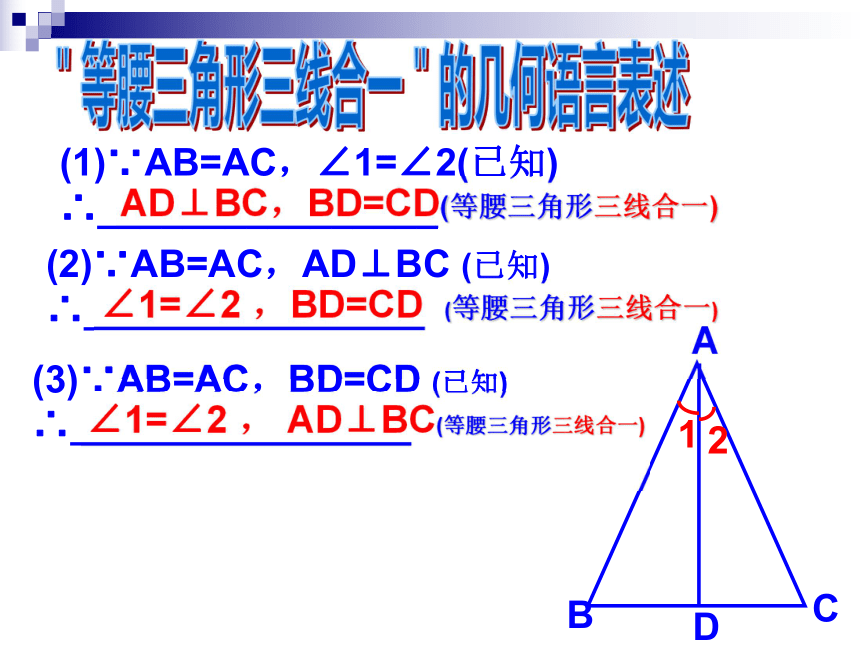
能用你的话说说吗？(1)∵AB=AC，∠1=∠2(已知)
∴________________＂等腰三角形三线合一＂的几何语言表述AD⊥BC，BD=CD(等腰三角形三线合一)(2)∵AB=AC，AD⊥BC (已知)
∴________________∠1=∠2 ，BD=CD (等腰三角形三线合一)
(3)∵AB=AC，BD=CD (已知)
∴________________∠1=∠2 ， AD⊥BC(等腰三角形三线合一)
判断：1、等腰三角形的角平分线、中线和高互相重合。
2、等腰三角形的顶角平分线一定垂直底边。
3、等腰三角形的角平分线、高线和中线的
总数一共能画出9条。
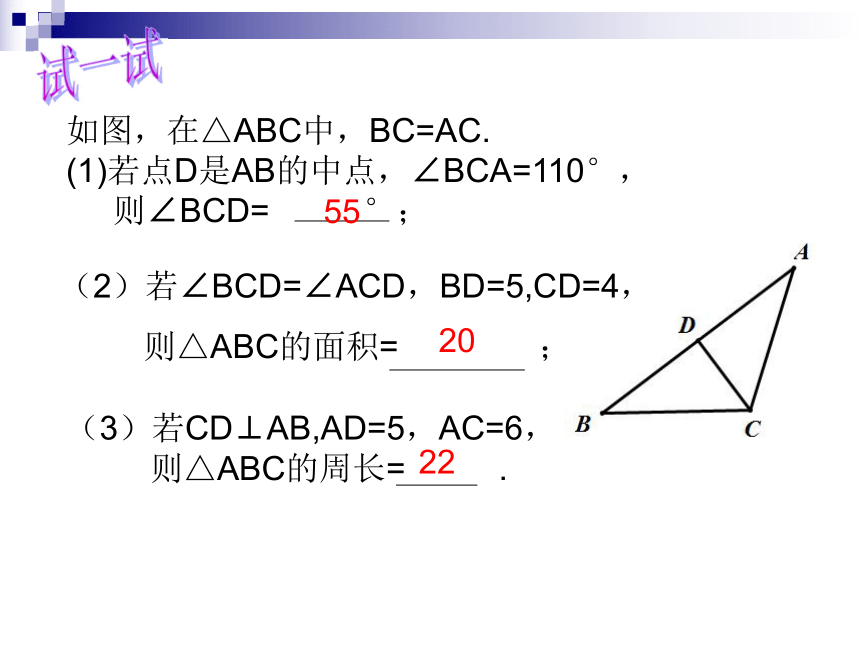
4、等腰三角形底边上的中线一定垂直于底边。（X）（√）（X）（√）如图，在△ABC中，BC=AC.
(1)若点D是AB的中点，∠BCA=110°，
则∠BCD= °；552220试一试用一用：例1.已知：如图，AD平分∠BAC，∠ABD=∠ACD.
(1)求证：AB=AC;
(2)连接BC，猜想AD与BC的位置关系？并说明理由.用一用：例2.已知线段a，h，用直尺和圆规作等腰三角形ABC，
使底边BC=a，底边BC边上的高线长为h. 作法：
1.作线段BC=a.
2.作线段BC的垂直平分线l，交BC于点D.
3.在直线l上截取DA=h，连接AB，AC.∴△ABC就是所求作的等腰三角形.要求:1.保留作图痕迹；2.写出结论.已知：如图，AC=AD，BC=BD，AB与CD相交于O点，求证：AB⊥CD拓展提高已知：如图，AC=AD，BC=BD，AB与CD相交于O点，求证：AB⊥CD证明：∵在△ABC和△ABD中AC=AD（已知）
BC=BD（已知）
AB=AB（公共边）∴△ ABC≌ △ABD（SSS）∴∠CAB=∠DAB（全等三角形对应角相等）又∵AC=AD∴ △ADO为等腰三角形（等腰三角形的定义）∴AO是△ABO的顶角平分线∴AO⊥CD（等腰三角形三线合一）∴AB⊥CD文字叙述几何语言等腰三角形的两底角相等
(同一个三角形中，等边对等角)∵AB=AC
∴∠B=∠C等腰三角形顶角的平分线、底边上的中线和高线互相重合
（简称等腰三角形三线合一）∵AB=AC，∠1=∠2 ∴AD⊥BC，BD=CD∵AB=AC， BD=CD ∴ ∠1=∠2 ，AD⊥BC∵AB=AC，AD⊥BC ∴ ∠1=∠2 ，BD=CD课堂小结自我提高1.已知：如图，在△ABC中，AB=AC, AD⊥BC ，
E为AD上一点，EF⊥AB，F为垂足，且EF=3.
则点E到边AC的距离是 . 2.已知：如图，在△ABC中，AB=AC，D为CA延长线上一点，
点F 在AB上，且AD=AF,连接DF并延长交BC于点E.
求证： DE⊥BC. G3H证明：过点A画AH⊥BC，H为垂足
∵AB=AC,AH⊥BC
∴∠BAH=∠CAH= ∠BAC
∵AF=AD
∴∠AFD=∠D
∵∠BAC=∠AFD+∠D
∴∠AFD=∠D= ∠BAC

∴∠AFD=∠BAH
∴DE∥AH
∴DE⊥BC