2.7 勾股定理（1）课件

课件25张PPT。LODAING…授课老师：肖美芳 我是地球人,I am a man on the earth…
﹌﹋ ﹠ ★ ◎ ▼ ♀ ♂其他星球上是否存在着“人”呢？为了探寻这一点，世界上许多科学家向宇宙发出了许多信号，如地球上人类的语言、音乐、各种图形等。哇！这是一种与外星人取得联系的什么图形？哦，据说我国著名的数学家华罗庚曾建议“发射”一种勾股定理的图形。如果宇宙“人”也拥有文明的话，那么他们一定会认识这种语言的，因为几乎所有具有古代文化的民族和国家都对勾股定理有所了解。勾股定理有着悠久的历史。
古巴比伦人和古代中国人看出了这个关系；
古希腊的毕达哥拉斯学派首先证明了这关系。
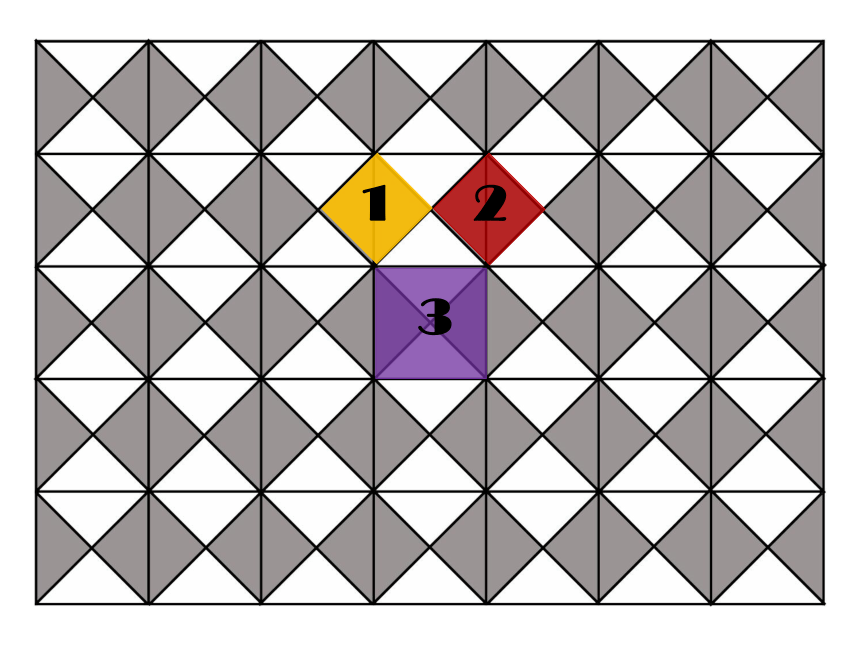
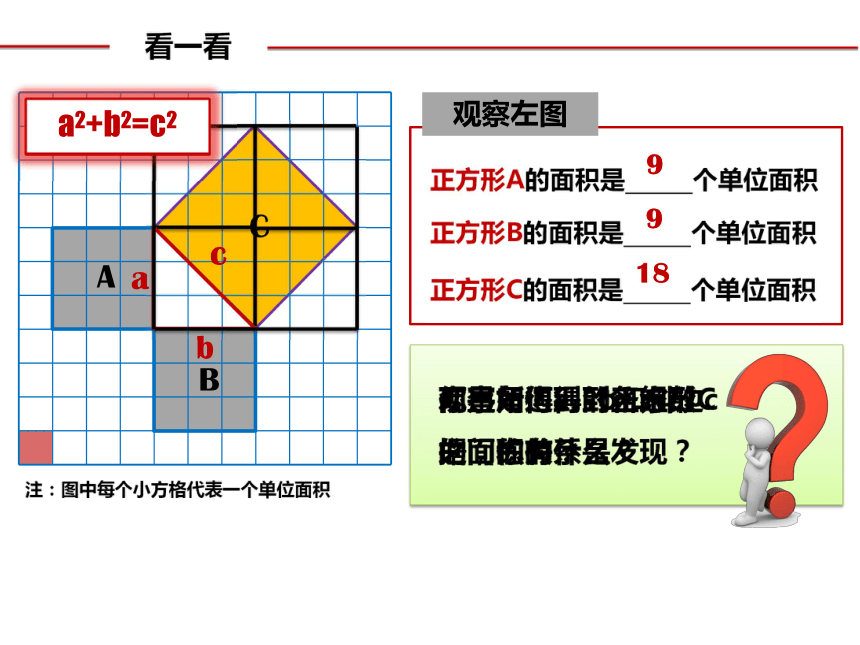
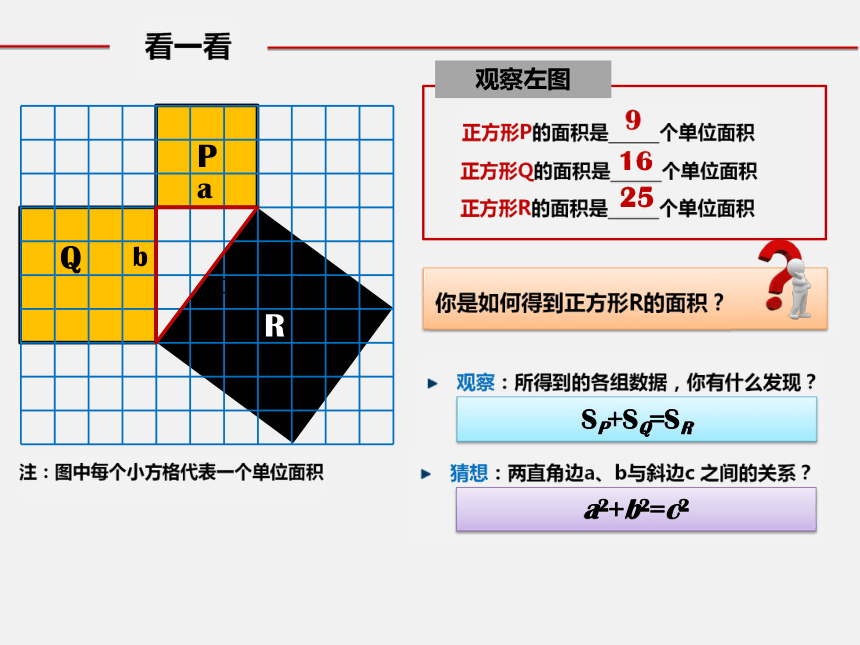
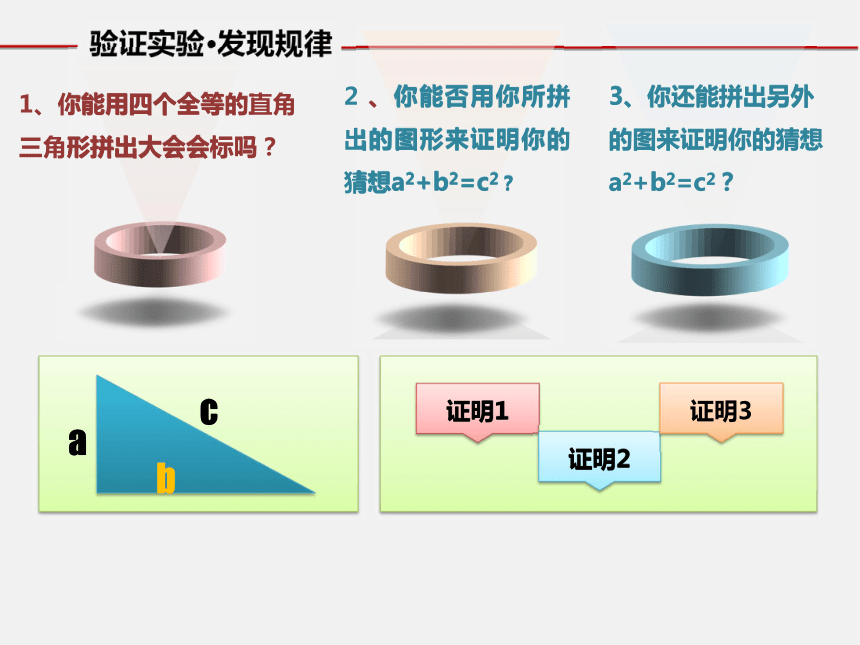
很多具有古代文化的民族和国家都会说：我们首先认识的数学定理是勾股定理。看一看相传两千多年前，一次毕达哥拉斯去朋友家作客，发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系，同学们，我们也来观察下面的图案，看看你能发现什么？智慧地板123看一看注：图中每个小方格代表一个单位面积ABC9918观察所得到的各组数据，你有什么发现？你是如何得到正方形C的面积的？SA+SB=SC两直角边a、b和斜边c之间的关系是？abca2+b2=c2看一看观察：所得到的各组数据，你有什么发现？SP+SQ=SR猜想：两直角边a、b与斜边c 之间的关系？a2+b2=c2abc注：图中每个小方格代表一个单位面积正方形Q的面积是 个单位面积正方形R的面积是 个单位面积91625正方形P的面积是 个单位面积2002年世界数学家大会会标验证实验·发现规律2 、你能否用你所拼出的图形来证明你的猜想a2+b2=c2？
3、你还能拼出另外的图来证明你的猜想a2+b2=c2？1、你能用四个全等的直角三角形拼出大会会标吗？证明1证明2证明3∵ c2==b2-2ab+a2+ 2ab =a2+b2∴a2+b2=c2大正方形的面积可以表示为 ；
也可以表示为 。c2该图2002年8月在北京召开的国际数学家大会的会标示意图，取材于我国古代数学著作《勾股圆方图》。证明1证明2∵ (a+b)2 = a2+2ab+b2 = 2ab +c2∴a2+b2=c2大正方形的面积可以表示为 ；
也可以表示为 。(a+b)2证明3拼一拼 试一试：你能只用这两个直角三角形来证明吗？又∵S梯形ABCD=S△AED+S△EBC+S△CED∴比较上面二式得c2=a2+b2青朱出入图勾股定理简介勾股定理曾引起很多人的兴趣，世界上目前对这个定理的证明方法共500多种，仅我国清末数学家华蘅芳就提供了20多种精彩的证法，至今可查的有关勾股定理的最早记载是大约公元前1世纪前后成书的我国古代的一部著名的数学著作《周脾算经》，比古希腊的著名数学家毕达哥拉斯的证明还要早五百多年。勾股定理直角三角形两直角边的平方和等于斜边的平方.
(人类最伟大的十个科学发现之一)abca2+b2=c2勾股弦辉煌发现我国早在三千多年就知道了这个定理，人们把弯曲成直角的手臂的上半部分称为“勾”，下半部分称为“股”，我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”。因此就把这一定理称为勾股定理。结论变形直角三角形中，两直角边的平方和等于斜边的平方考一考1、求下列图中表示边的未知数x、y、z的值。A81144BC144169352255X
2、在△ABC中，∠C=90°,如果c=10，a=6，那么△ABC的面积为 。z4y24美丽的毕达哥拉斯树小 结定理内容 定理应用 从特殊到一般、数形结合思想 重要的思想方法及数学思想 作业快餐勾股定理又称毕达哥拉斯定理，下面据传是当年毕达哥拉斯发现勾股定理时做出的证明。 将4个全等的直角三角形拼成边长为(a＋b)的正方形ABCD，使中间留下边长c的一个正方形洞。画出正方形ABCD。移动三角形至图2所示的位置中，于是留下了边长分别为a与b的两个正方形洞。则图1和图2中的白色部分面积必定相等，所以c2=a2+b2。课后阅读教师寄语要养成用数学的思维去解读世界的习惯。
只有不断的思考，才会有新的发现；只有量的变化，才会有质的进步。
其实数学在我们的生活中无处不在, 只要你是个有心人,就一定会发现在我们的身边,我们的眼前, 还有很多象 “勾股定理”那样的知识等待我们去探索，等待我们去发现……看一看QPRQP用了“补”的方法R用了“割”的方法如图，小方格的边长为1。你能求出正方形R的面积吗？