2022-2023学年浙教版八年级数学上册2.7探索勾股定理 同步练习题 (含答案)
文档属性
| 名称 | 2022-2023学年浙教版八年级数学上册2.7探索勾股定理 同步练习题 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 296.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 20:46:58 | ||
图片预览


文档简介
2022-2023学年浙教版八年级数学上册《2.7探索勾股定理》同步练习题(附答案)
一.选择题
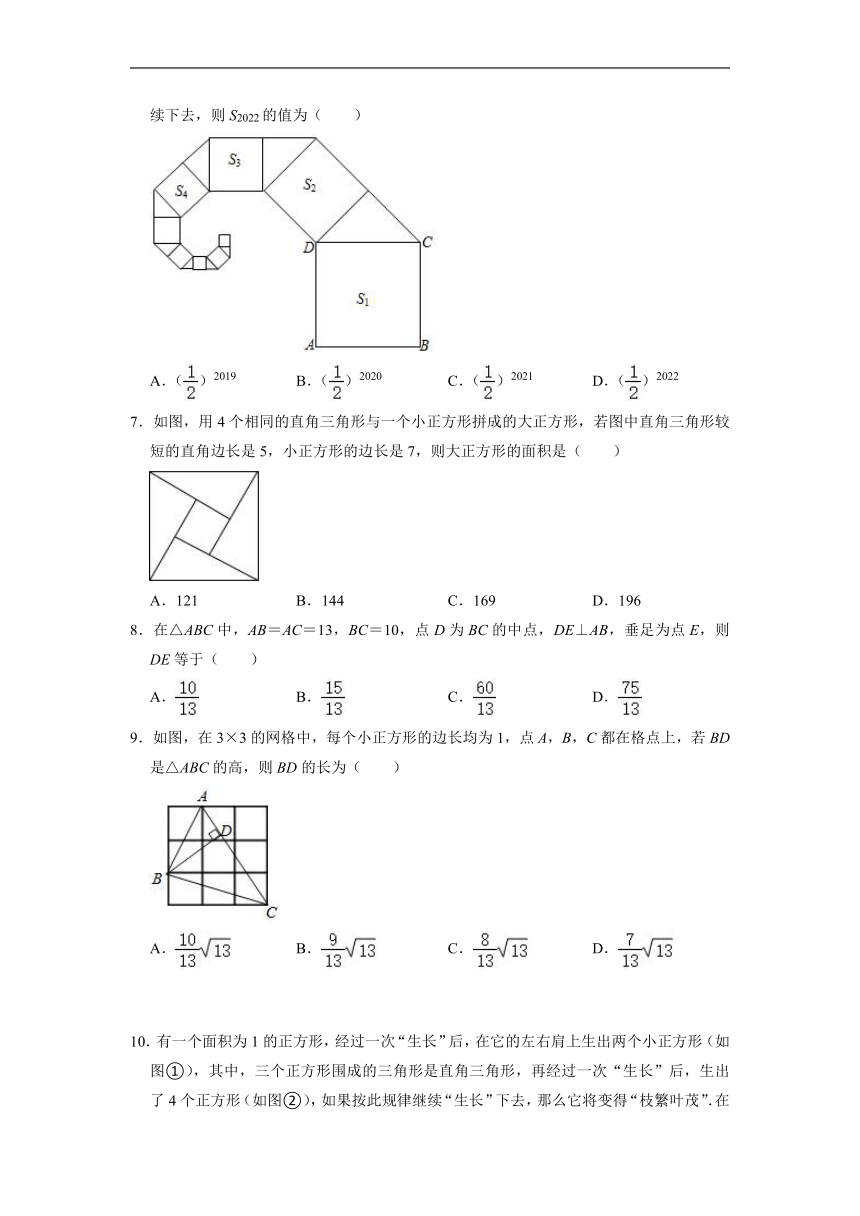
1.如图,在Rt△ABC中,∠ACB=90°,以AC为边在△ABC外作正方形,其面积为9,以BC为斜边在△ABC外作等腰直角三角形,其面积为4,则AB=( )
A.5 B.7 C. D.
2.如图,设小方格的面积为1,则图中以格点为端点且长度为的线段有( )
A.2条 B.3条 C.4条 D.5条
3.如图,是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中AE=10,BE=24,则EF的长是( )
A.14 B.13 C.14 D.14
4.一个直角三角形的两直角边长分别为3,4,则第三边长是( )
A.3 B.4 C.5 D.5或
5.如图所示:是一段楼梯,高BC是3m,斜边AC是5m,如果在楼梯上铺地毯,那么至少需要地毯( )
A.5m B.6m C.7m D.8m
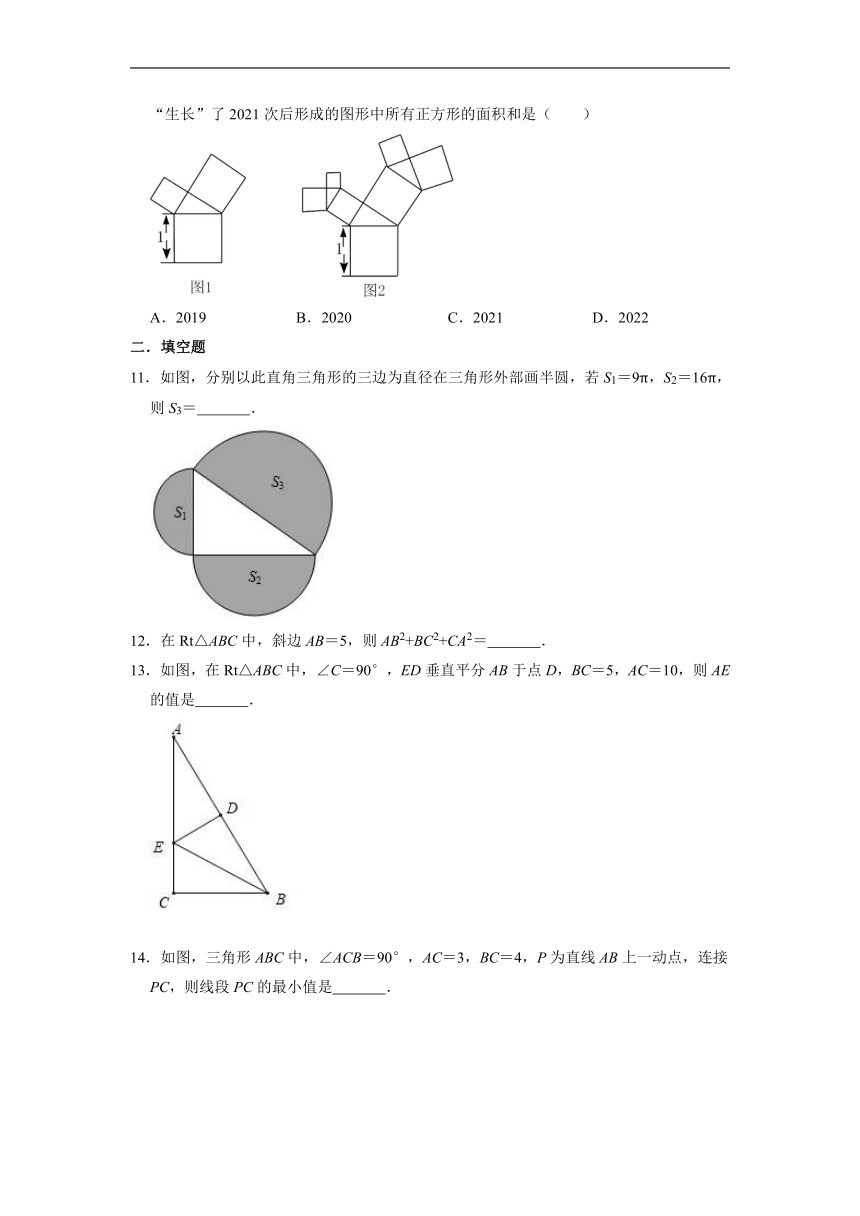
6.如图,正方形ABCD的边长为2.面积标记为S1.以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2022的值为( )
A.()2019 B.()2020 C.()2021 D.()2022
7.如图,用4个相同的直角三角形与一个小正方形拼成的大正方形,若图中直角三角形较短的直角边长是5,小正方形的边长是7,则大正方形的面积是( )
A.121 B.144 C.169 D.196
8.在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于( )
A. B. C. D.
9.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )
A. B. C. D.
10.有一个面积为1的正方形,经过一次“生长”后,在它的左右肩上生出两个小正方形(如图①),其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,生出了4个正方形(如图②),如果按此规律继续“生长”下去,那么它将变得“枝繁叶茂”.在“生长”了2021次后形成的图形中所有正方形的面积和是( )
A.2019 B.2020 C.2021 D.2022
二.填空题
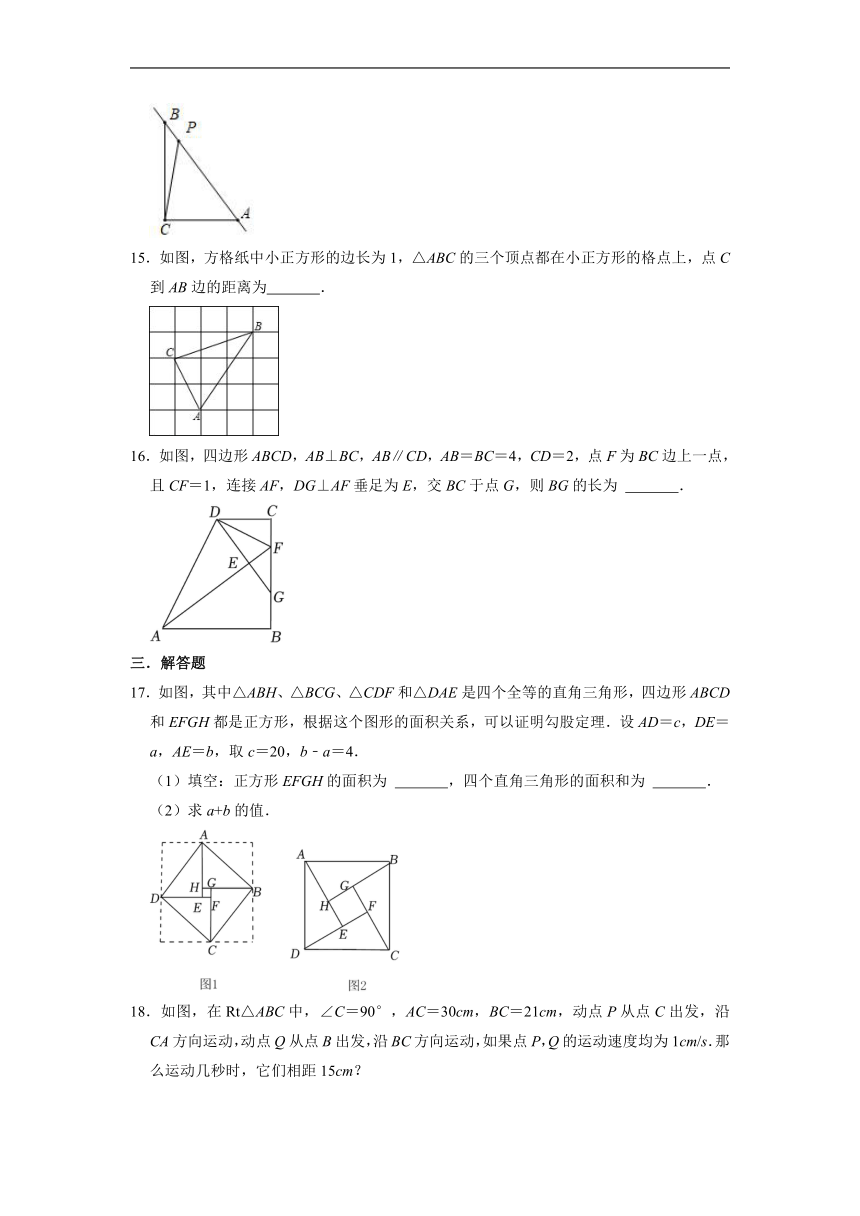
11.如图,分别以此直角三角形的三边为直径在三角形外部画半圆,若S1=9π,S2=16π,则S3= .
12.在Rt△ABC中,斜边AB=5,则AB2+BC2+CA2= .
13.如图,在Rt△ABC中,∠C=90°,ED垂直平分AB于点D,BC=5,AC=10,则AE的值是 .
14.如图,三角形ABC中,∠ACB=90°,AC=3,BC=4,P为直线AB上一动点,连接PC,则线段PC的最小值是 .
15.如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,点C到AB边的距离为 .
16.如图,四边形ABCD,AB⊥BC,AB∥CD,AB=BC=4,CD=2,点F为BC边上一点,且CF=1,连接AF,DG⊥AF垂足为E,交BC于点G,则BG的长为 .
三.解答题
17.如图,其中△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,根据这个图形的面积关系,可以证明勾股定理.设AD=c,DE=a,AE=b,取c=20,b﹣a=4.
(1)填空:正方形EFGH的面积为 ,四个直角三角形的面积和为 .
(2)求a+b的值.
18.如图,在Rt△ABC中,∠C=90°,AC=30cm,BC=21cm,动点P从点C出发,沿CA方向运动,动点Q从点B出发,沿BC方向运动,如果点P,Q的运动速度均为1cm/s.那么运动几秒时,它们相距15cm?
19.如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=3cm,AB=8cm,求图中阴影部分的面积.
20.如图,在等腰△ABC中,AB=BC=20,点D为AB上一点,且CD=16,BD=12,求AC的长.
参考答案
一.选择题
1.解:∵以AC为边在△ABC外作正方形,其面积为9,以BC为斜边在△ABC外作等腰直角三角形,其面积为4,
∴BC=4,AC=3,
在Rt△ABC中,∠ACB=90°,
由勾股定理得,AB=,
故选:A.
2.解:∵=,
∴是直角边长为2,3的直角三角形的斜边,
如图所示,AB,CD,BE,DF的长都等于;
故选:C.
3.解:∵AE=10,BE=24,即24和10为两条直角边长时,
小正方形的边长=24﹣10=14,
∴EF==14.
故选:D.
4.解:已知直角三角形的两直角边为3、4,
则第三边长为=5,
故选:C.
5.解:∵△ABC是直角三角形,BC=3m,AC=5m
∴AB===4m,
∴如果在楼梯上铺地毯,那么至少需要地毯为AB+BC=7米.
故选:C.
6.解:如图所示,
∵△CDE是等腰直角三角形,
∴DE=CE,∠CED=90°,
∴CD2=DE2+CE2=2DE2,
∴DE=CD,
即等腰直角三角形的直角边为斜边的倍,
∴S1=22=4=4×()0,
S2=(2×)2=2=4×()1,
S3=(×)2=1=4×()2,
S4=(1×)2==4×()3,
…,
∴Sn=4×()n﹣1,
∴S2022=4×()2021=()2019.
故选:A.
7.解:∵直角三角形较短的直角边长是5,小正方形的边长是7,
∴直角三角形的较长直角边=5+7=12,
∴直角三角形斜边长=13,
∴大正方形的边长是13,
∴大正方形的面积是13×13=169.
故选:C.
8.解:连接AD,
∵△ABC中,AB=AC=13,BC=10,D为BC中点,
∴AD⊥BC,BD=BC=5,
∴AD==12,
又∵DE⊥AB,
∴S△ABD=BD AD=AB ED,
∴ED=,
故选:C.
9.解:由勾股定理得:AC==,
∵S△ABC=3×3﹣=3.5,
∴,
∴,
∴BD=,
故选:D.
10.解:设直角三角形的是三条边分别是a,b,c.
根据勾股定理,得a2+b2=c2,
即正方形A的面积+正方形B的面积=正方形C的面积=1.
推而广之,“生长”了2021次后形成的图形中所有的正方形的面积和是2022×1=2022.
故选:D.
二.填空题
11.解:设面积为S1的半圆的直径为a,面积为S2的半圆的直径为b,面积为S3的半圆的直径为c,
由勾股定理得:a2+b2=c2,
由题意得:×π×()2=9π,×π×()2=16π,
则a2=72,b2=128,
∴c2=200,
∴S3=×π×()2=25π,
故答案为:25π.
12.解:∵在Rt△ABC中,斜边AB=5,
∴AB2=BC2+CA2=25,
∴AB2+BC2+CA2=25+25=50.
故答案为:50.
13.解:∵ED垂直平分AB于点D,
∴AE=BE,
设AE=x,则BE=x,
故在Rt△ECB中,
EC2+BC2=EB2,
(10﹣x)2+52=x2,
解得:x=.
故答案为:.
14.解:作CP⊥AB于P,
由垂线段最短可知,此时PC最小,
由勾股定理得,AB===5,
S△ABC=×AC×BC=×AB×PC,即×3×4=×5×PC,
解得,PC=,
故答案为:.
15.解:∵S△ABC=3×3﹣×1×2﹣×2×3﹣×1×3=,AB==,
∴点C到AB边的距离==.
故答案为:.
16.解:连接AG,过点D作DM⊥AB于点M,则四边形DMBC为矩形,
∴DM=BC=4,
∴AD===2,
∵CF=1,BC=AB=4,
∴BF=3,
∴AF===5,
∵DC=2,
∴DF==,
设EF=x,则AE=5﹣x,
∵AD2﹣AE2=DF2﹣EF2,
∴,
∴x=1,
∴EF=1,
∴AE=4,
∴AE=AB,
在Rt△AEG和Rt△ABG中,
,
∴Rt△AEG≌Rt△ABG(HL),
∴EG=BG,
设BG=y,则EG=3﹣y,
∵EF2+EG2=FG2,
∴12+y2=(3﹣y)2,
∴y=,
∴BG=,
故答案为:;
三.解答题
17.解:(1)∵HE=b﹣a=4,
∴S正方形EFGH=HE2=16,
∵AD=c=20,
∴S正方形ABCD=AD2=400,
∴四个直角三角形的面积和=S正方形ABCD﹣S正方形EFGH=400﹣16=384,
故答案为:16;384;
(2)由(1)可知四个直角三角形的面积和为384,
∴4×ab=384,解得2ab=384,
∵a2+b2=c2=400,
∴(a+b)2=a2+b2+2ab=400+384=784.
∴a+b=28(负值舍去).
18.解:设运动x秒时,它们相距15cm,则CP=xcm,CQ=(21﹣x)cm,依题意有
x2+(21﹣x)2=152,
解得x1=9,x2=12.
故运动9秒或12秒时,它们相距15cm.
19.解:由折叠可知△ADE和△AFE关于AE成轴对称,
故AF=AD,EF=DE=DC﹣CE=8﹣3=5.
所以CF=4,
设BF=xcm,则AF=AD=BC=x+4.
在Rt△ABF中,由勾股定理,得82+x2=(x+4)2.
解得x=6,故BC=10.
所以阴影部分的面积为:10×8﹣2S△ADE=80﹣50=30(cm2).
20.解:∵BC=20,CD=16,BD=12,
∴BD2+CD2=122+162=400=BC2,
∴△BCD是直角三角形,且∠BDC=90°,
∴∠ADC=90°.
在Rt△ACD中,AD=AB﹣BD=20﹣12=8,
∴AC===8.
一.选择题
1.如图,在Rt△ABC中,∠ACB=90°,以AC为边在△ABC外作正方形,其面积为9,以BC为斜边在△ABC外作等腰直角三角形,其面积为4,则AB=( )
A.5 B.7 C. D.
2.如图,设小方格的面积为1,则图中以格点为端点且长度为的线段有( )
A.2条 B.3条 C.4条 D.5条
3.如图,是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中AE=10,BE=24,则EF的长是( )
A.14 B.13 C.14 D.14
4.一个直角三角形的两直角边长分别为3,4,则第三边长是( )
A.3 B.4 C.5 D.5或
5.如图所示:是一段楼梯,高BC是3m,斜边AC是5m,如果在楼梯上铺地毯,那么至少需要地毯( )
A.5m B.6m C.7m D.8m
6.如图,正方形ABCD的边长为2.面积标记为S1.以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2022的值为( )
A.()2019 B.()2020 C.()2021 D.()2022
7.如图,用4个相同的直角三角形与一个小正方形拼成的大正方形,若图中直角三角形较短的直角边长是5,小正方形的边长是7,则大正方形的面积是( )
A.121 B.144 C.169 D.196
8.在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于( )
A. B. C. D.
9.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )
A. B. C. D.
10.有一个面积为1的正方形,经过一次“生长”后,在它的左右肩上生出两个小正方形(如图①),其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,生出了4个正方形(如图②),如果按此规律继续“生长”下去,那么它将变得“枝繁叶茂”.在“生长”了2021次后形成的图形中所有正方形的面积和是( )
A.2019 B.2020 C.2021 D.2022
二.填空题
11.如图,分别以此直角三角形的三边为直径在三角形外部画半圆,若S1=9π,S2=16π,则S3= .
12.在Rt△ABC中,斜边AB=5,则AB2+BC2+CA2= .
13.如图,在Rt△ABC中,∠C=90°,ED垂直平分AB于点D,BC=5,AC=10,则AE的值是 .
14.如图,三角形ABC中,∠ACB=90°,AC=3,BC=4,P为直线AB上一动点,连接PC,则线段PC的最小值是 .
15.如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,点C到AB边的距离为 .
16.如图,四边形ABCD,AB⊥BC,AB∥CD,AB=BC=4,CD=2,点F为BC边上一点,且CF=1,连接AF,DG⊥AF垂足为E,交BC于点G,则BG的长为 .
三.解答题
17.如图,其中△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,根据这个图形的面积关系,可以证明勾股定理.设AD=c,DE=a,AE=b,取c=20,b﹣a=4.
(1)填空:正方形EFGH的面积为 ,四个直角三角形的面积和为 .
(2)求a+b的值.
18.如图,在Rt△ABC中,∠C=90°,AC=30cm,BC=21cm,动点P从点C出发,沿CA方向运动,动点Q从点B出发,沿BC方向运动,如果点P,Q的运动速度均为1cm/s.那么运动几秒时,它们相距15cm?
19.如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=3cm,AB=8cm,求图中阴影部分的面积.
20.如图,在等腰△ABC中,AB=BC=20,点D为AB上一点,且CD=16,BD=12,求AC的长.
参考答案
一.选择题
1.解:∵以AC为边在△ABC外作正方形,其面积为9,以BC为斜边在△ABC外作等腰直角三角形,其面积为4,
∴BC=4,AC=3,
在Rt△ABC中,∠ACB=90°,
由勾股定理得,AB=,
故选:A.
2.解:∵=,
∴是直角边长为2,3的直角三角形的斜边,
如图所示,AB,CD,BE,DF的长都等于;
故选:C.
3.解:∵AE=10,BE=24,即24和10为两条直角边长时,
小正方形的边长=24﹣10=14,
∴EF==14.
故选:D.
4.解:已知直角三角形的两直角边为3、4,
则第三边长为=5,
故选:C.
5.解:∵△ABC是直角三角形,BC=3m,AC=5m
∴AB===4m,
∴如果在楼梯上铺地毯,那么至少需要地毯为AB+BC=7米.
故选:C.
6.解:如图所示,
∵△CDE是等腰直角三角形,
∴DE=CE,∠CED=90°,
∴CD2=DE2+CE2=2DE2,
∴DE=CD,
即等腰直角三角形的直角边为斜边的倍,
∴S1=22=4=4×()0,
S2=(2×)2=2=4×()1,
S3=(×)2=1=4×()2,
S4=(1×)2==4×()3,
…,
∴Sn=4×()n﹣1,
∴S2022=4×()2021=()2019.
故选:A.
7.解:∵直角三角形较短的直角边长是5,小正方形的边长是7,
∴直角三角形的较长直角边=5+7=12,
∴直角三角形斜边长=13,
∴大正方形的边长是13,
∴大正方形的面积是13×13=169.
故选:C.
8.解:连接AD,
∵△ABC中,AB=AC=13,BC=10,D为BC中点,
∴AD⊥BC,BD=BC=5,
∴AD==12,
又∵DE⊥AB,
∴S△ABD=BD AD=AB ED,
∴ED=,
故选:C.
9.解:由勾股定理得:AC==,
∵S△ABC=3×3﹣=3.5,
∴,
∴,
∴BD=,
故选:D.
10.解:设直角三角形的是三条边分别是a,b,c.
根据勾股定理,得a2+b2=c2,
即正方形A的面积+正方形B的面积=正方形C的面积=1.
推而广之,“生长”了2021次后形成的图形中所有的正方形的面积和是2022×1=2022.
故选:D.
二.填空题
11.解:设面积为S1的半圆的直径为a,面积为S2的半圆的直径为b,面积为S3的半圆的直径为c,
由勾股定理得:a2+b2=c2,
由题意得:×π×()2=9π,×π×()2=16π,
则a2=72,b2=128,
∴c2=200,
∴S3=×π×()2=25π,
故答案为:25π.
12.解:∵在Rt△ABC中,斜边AB=5,
∴AB2=BC2+CA2=25,
∴AB2+BC2+CA2=25+25=50.
故答案为:50.
13.解:∵ED垂直平分AB于点D,
∴AE=BE,
设AE=x,则BE=x,
故在Rt△ECB中,
EC2+BC2=EB2,
(10﹣x)2+52=x2,
解得:x=.
故答案为:.
14.解:作CP⊥AB于P,
由垂线段最短可知,此时PC最小,
由勾股定理得,AB===5,
S△ABC=×AC×BC=×AB×PC,即×3×4=×5×PC,
解得,PC=,
故答案为:.
15.解:∵S△ABC=3×3﹣×1×2﹣×2×3﹣×1×3=,AB==,
∴点C到AB边的距离==.
故答案为:.
16.解:连接AG,过点D作DM⊥AB于点M,则四边形DMBC为矩形,
∴DM=BC=4,
∴AD===2,
∵CF=1,BC=AB=4,
∴BF=3,
∴AF===5,
∵DC=2,
∴DF==,
设EF=x,则AE=5﹣x,
∵AD2﹣AE2=DF2﹣EF2,
∴,
∴x=1,
∴EF=1,
∴AE=4,
∴AE=AB,
在Rt△AEG和Rt△ABG中,
,
∴Rt△AEG≌Rt△ABG(HL),
∴EG=BG,
设BG=y,则EG=3﹣y,
∵EF2+EG2=FG2,
∴12+y2=(3﹣y)2,
∴y=,
∴BG=,
故答案为:;
三.解答题
17.解:(1)∵HE=b﹣a=4,
∴S正方形EFGH=HE2=16,
∵AD=c=20,
∴S正方形ABCD=AD2=400,
∴四个直角三角形的面积和=S正方形ABCD﹣S正方形EFGH=400﹣16=384,
故答案为:16;384;
(2)由(1)可知四个直角三角形的面积和为384,
∴4×ab=384,解得2ab=384,
∵a2+b2=c2=400,
∴(a+b)2=a2+b2+2ab=400+384=784.
∴a+b=28(负值舍去).
18.解:设运动x秒时,它们相距15cm,则CP=xcm,CQ=(21﹣x)cm,依题意有
x2+(21﹣x)2=152,
解得x1=9,x2=12.
故运动9秒或12秒时,它们相距15cm.
19.解:由折叠可知△ADE和△AFE关于AE成轴对称,
故AF=AD,EF=DE=DC﹣CE=8﹣3=5.
所以CF=4,
设BF=xcm,则AF=AD=BC=x+4.
在Rt△ABF中,由勾股定理,得82+x2=(x+4)2.
解得x=6,故BC=10.
所以阴影部分的面积为:10×8﹣2S△ADE=80﹣50=30(cm2).
20.解:∵BC=20,CD=16,BD=12,
∴BD2+CD2=122+162=400=BC2,
∴△BCD是直角三角形,且∠BDC=90°,
∴∠ADC=90°.
在Rt△ACD中,AD=AB﹣BD=20﹣12=8,
∴AC===8.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
