1.4全等三角形-提升练习 2022—2023学年浙教版数学八年级上册(含答案)
文档属性
| 名称 | 1.4全等三角形-提升练习 2022—2023学年浙教版数学八年级上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 225.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 23:25:11 | ||
图片预览



文档简介
浙教版-8年级-上册-数学-第1章《三角形的初步知识》
1.4全等三角形
【知识点-部分】
要点一、全等图形:形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等图形.
要点诠释:一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.两个全等形的周长相等,面积相等。
要点二、全等三角形:能够完全重合的两个三角形叫全等三角形。
要点三、对应顶点,对应边,对应角
1、对应顶点,对应边,对应角定义:两个全等三角形重合在一起,
重合的顶点叫对应顶点,重合的边叫对应边,重合的角叫对应角.
要点诠释:
1、在写两个三角形全等时,通常把对应顶点的字母写在对应位置上,这样容易找出对应边、对应角.如下图,△ABC与△DEF全等,记作△ABC≌△DEF,其中点A和点D,点B和点E,点C和点F是对应顶点;AB和DE,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角。
2、找对应边、对应角的方法
(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;
(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角;
(3)有公共边的,公共边是对应边; (4)有公共角的,公共角是对应角;
(5)有对顶角的,对顶角一定是对应角;
(6)两个全等三角形中一对最长的边(或最大的角)是对应边(或角),一对最短的边(或最小的角)是对应边
(或角),等等。
要点四、全等三角形的性质
1、全等三角形的对应边相等; 2、全等三角形的对应角相等。
要点诠释:全等三角形对应边上的高相等,对应边上的中线相等,周长相等,面积相等.全等三角形的性质是今后研究其它全等图形的重要工具。
【典型例题-精选部分】
1、如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,
(1)当DE=8,BC=5时,线段AE的长为 ;
(2)已知∠D=35°,∠C=60°,① 求∠DBC的度数;② 求∠AFD的度数.
2、如图所示,D,A,E在同一条直线上,BD⊥DE于D,CE⊥DE于E,且△ABD≌△CAE,AD=2cm,BD=4cm,求
(1)DE的长; (2)∠BAC的度数.
3、如图,点A、B、C、D在同一条直线上,点E、F是直线.AD上方的点,连接AE、CE、BF、DF,
若△ACE≌△FDB,FD=3,AD=8.
(1)判断直线CE与DF是否平行?并说明理由; (2)求CD的长;
(3)若∠E=26°,∠F=53°,求∠ACE的度数.
4、如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P,若AD=DC=2.4,BC=4.1.
(1)若∠ABE=162°,∠DBC=30°,求∠CBE的度数; (2)求△DCP与△BPE的周长和.
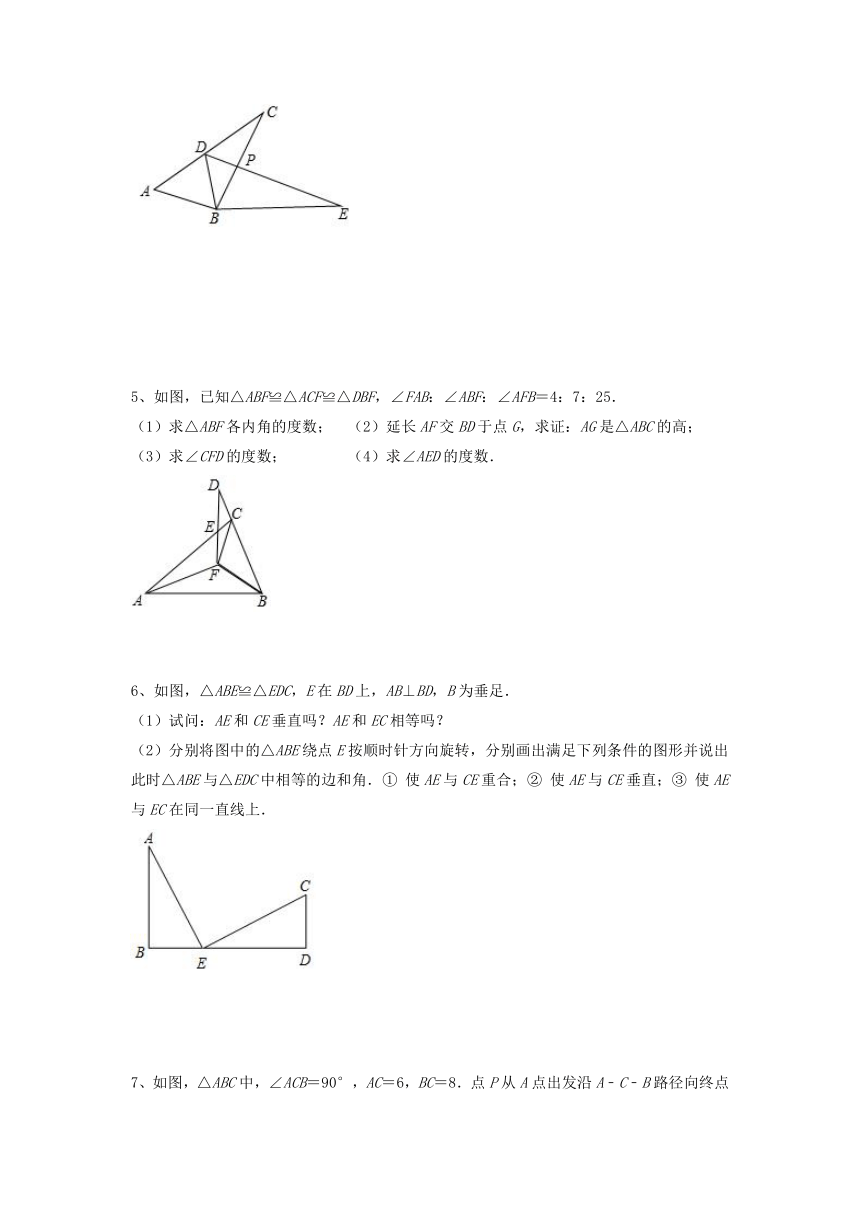
5、如图,已知△ABF≌△ACF≌△DBF,∠FAB:∠ABF:∠AFB=4:7:25.
(1)求△ABF各内角的度数; (2)延长AF交BD于点G,求证:AG是△ABC的高;
(3)求∠CFD的度数; (4)求∠AED的度数.
6、如图,△ABE≌△EDC,E在BD上,AB⊥BD,B为垂足.
(1)试问:AE和CE垂直吗?AE和EC相等吗?
(2)分别将图中的△ABE绕点E按顺时针方向旋转,分别画出满足下列条件的图形并说出此时△ABE与△EDC中相等的边和角.① 使AE与CE重合;② 使AE与CE垂直;③ 使AE与EC在同一直线上.
7、如图,△ABC中,∠ACB=90°,AC=6,BC=8.点P从A点出发沿A﹣C﹣B路径向终点运动,终点为B点;点Q从B点出发沿B﹣C﹣A路径向终点运动,终点为A点.点P和Q分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.问:点P运动多少时间时,△PEC与△QFC全等?请说明理由.
8、我们把两组对边分别平行的四边形定义为平行四边形,同样的道理,我们也可以把至少有一组邻边相等的四边形定义为等邻边四边形.把对角互补的等邻边四边形定义为完美等邻边四边形.
(1)请写出一个你学过的特殊四边形中是等邻边四边形的图形的名称;
(2)已知,如图,完美等邻边四边形ABCD,AD=CD,∠B+∠D=180°,连接对角线AC,BD,请你结合图形,写出完美等邻边四边形的一条性质;
(3)在四边形ABCD中,若∠B+∠D=180°,且BD平分∠ABC时,求证:四边形ABCD是完美等邻边四边形.
9、如图①,在Rt△ABC中,∠C=90°,BC=9cm,AC=12cm,AB=15cm,现有一动点P,从点A出发,沿着三角形的边AC→CB→BA运动,回到点A停止,速度为3cm/s,设运动时间为ts.
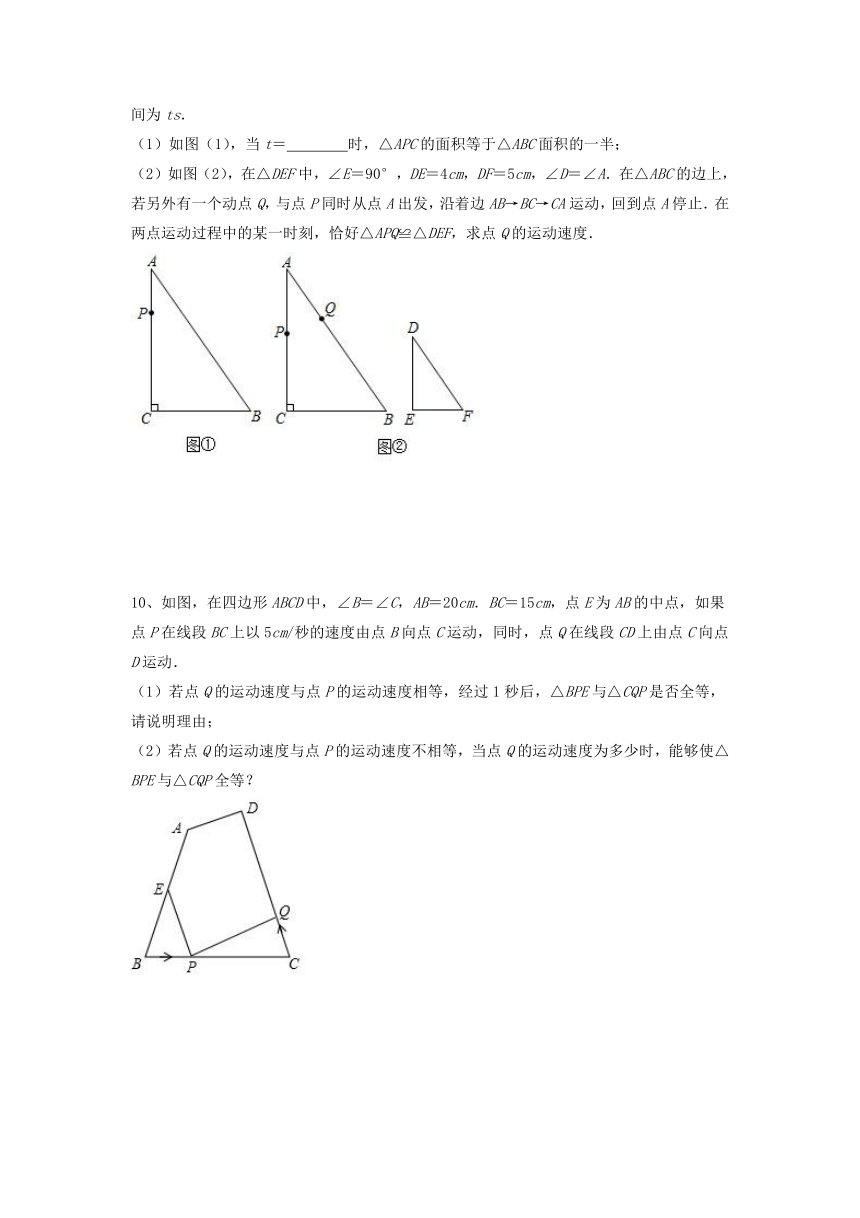
(1)如图(1),当t= 时,△APC的面积等于△ABC面积的一半;
(2)如图(2),在△DEF中,∠E=90°,DE=4cm,DF=5cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边AB→BC→CA运动,回到点A停止.在两点运动过程中的某一时刻,恰好△APQ≌△DEF,求点Q的运动速度.
10、如图,在四边形ABCD中,∠B=∠C,AB=20cm.BC=15cm,点E为AB的中点,如果点P在线段BC上以5cm/秒的速度由点B向点C运动,同时,点Q在线段CD上由点C向点D运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPE与△CQP是否全等,请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPE与△CQP全等?
【参考答案】
1、如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,
(1)当DE=8,BC=5时,线段AE的长为 ;
(2)已知∠D=35°,∠C=60°,① 求∠DBC的度数;② 求∠AFD的度数.
【解答】解:(1)∵△ABC≌△DEB,DE=8,BC=5,∴AB=DE=8,BE=BC=5,∴AE=AB﹣BE=8﹣5=3;
(2)① ∵△ABC≌△DEB∴∠A=∠D=35°,∠DBE=∠C=60°,∵∠A+∠ABC+∠C=180°,
∴∠ABC=180°﹣∠A﹣∠C=85°,∴∠DBC=∠ABC﹣∠DBE=85°﹣60°=25°;
② ∵∠AEF是△DBE的外角,∴∠AEF=∠D+∠DBE=35°+60°=95°,
∵∠AFD是△AEF的外角,∴∠AFD=∠A+∠AEF=35°+95°=130°.
2、如图所示,D,A,E在同一条直线上,BD⊥DE于D,CE⊥DE于E,且△ABD≌△CAE,AD=2cm,BD=4cm,求
(1)DE的长; (2)∠BAC的度数.
【解答】解:(1)∵△ABD≌△CAE,AD=2cm,BD=4cm,∴AE=BD=4cm,∴DE=AD+AE=6cm;
(2)∵BD⊥DE,∴∠D=90°,∴∠DBA+∠BAD=90°,∵△ABD≌△CAE,
∴∠DBA=∠CAE∴∠BAD+∠CAE=90°,∴∠BAC=90°.
3、如图,点A、B、C、D在同一条直线上,点E、F是直线.AD上方的点,连接AE、CE、BF、DF,
若△ACE≌△FDB,FD=3,AD=8.
(1)判断直线CE与DF是否平行?并说明理由; (2)求CD的长;
(3)若∠E=26°,∠F=53°,求∠ACE的度数.
【解答】解:(1)CE∥DF, 理由:∵△ACE≌△FDB,∴∠ACE=∠D,∴CE∥DF;
(2)∵△ACE≌△FDB,∴AC=DF=3,∵AD=8,∴CD=AD﹣AC=8﹣3=5;
(3)∵△ACE≌△FDB,∴∠DBF=∠E=26°,∵CE∥DF,∴∠1=∠F=53°,∴∠ACE=180°﹣26°﹣53°=101°
4、如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P,若AD=DC=2.4,BC=4.1.
(1)若∠ABE=162°,∠DBC=30°,求∠CBE的度数; (2)求△DCP与△BPE的周长和.
【解答】解:(1)∵∠ABE=162°,∠DBC=30°,∴∠ABD+∠CBE=132°,∵△ABC≌△DBE,∴∠ABC=∠DBE,
∴∠ABD=∠CBE=132°÷2=66°,即∠CBE的度数为66°;
(2)∵△ABC≌△DBE,∴DE=AD+DC=4.8,BE=BC=4.1,
△DCP和△BPE的周长和=DC+DP+CP+BP+PE+BE=DC+DE+BC+BE=15.4.
5、如图,已知△ABF≌△ACF≌△DBF,∠FAB:∠ABF:∠AFB=4:7:25.
(1)求△ABF各内角的度数; (2)延长AF交BD于点G,求证:AG是△ABC的高;
(3)求∠CFD的度数; (4)求∠AED的度数.
【解答】解:(1)∵∠FAB:∠ABF:∠AFB=4:7:25,
∴∠FAB=180°×=20°,∠ABF=180°×=35°,∠AFB=180°×=125°;
(2)证明:∵△ABF≌△ACF,∴AB=AC,∠BAF=∠CAF,∴AG是等腰△ABC顶角的平分线,
∴AG是△ABC的高(等腰三角形三线合一);
(3)解:∵△ABF≌△ACF≌△DBF,∴∠AFC=∠BFD=∠AFB=125°,
∴∠AFE=360°﹣∠AFB﹣∠BFD=360°﹣125°﹣125°=110°,∴∠CFD=∠AFC﹣∠AFE=125°﹣110°=15°;
(4)解:∵△ABF≌△ACF,∴∠FAC=∠FAB=20°,
由三角形的外角性质得,∠AED=∠FAC+∠AFE=20°+110°=130°.
6、如图,△ABE≌△EDC,E在BD上,AB⊥BD,B为垂足.
(1)试问:AE和CE垂直吗?AE和EC相等吗?
(2)分别将图中的△ABE绕点E按顺时针方向旋转,分别画出满足下列条件的图形并说出此时△ABE与△EDC中相等的边和角.① 使AE与CE重合;② 使AE与CE垂直;③ 使AE与EC在同一直线上.
【解答】解:(1)∵△ABE≌△EDC,∴AE=EC,∠A=∠CED,∵AB⊥BD,∴∠A+∠AEB=90°,
∴∠CED+∠AEB=90°,∴∠AEC=180°﹣90°=90°,∴AE⊥CE;
(2)如图所示,相等的边有AB=ED,AE=EC,BE=DC,
相等的角有∠BAE=∠DEC,∠ABE=∠EDC,∠AEB=∠ECD.
7、如图,△ABC中,∠ACB=90°,AC=6,BC=8.点P从A点出发沿A﹣C﹣B路径向终点运动,终点为B点;点Q从B点出发沿B﹣C﹣A路径向终点运动,终点为A点.点P和Q分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.问:点P运动多少时间时,△PEC与△QFC全等?请说明理由.
【解答】解:设运动时间为t秒时,△PEC与△QFC全等,∵△PEC与△QFC全等,∴斜边CP=CQ,
有四种情况:① P在AC上,Q在BC上,CP=6﹣t,CQ=8﹣3t,∴6﹣t=8﹣3t,∴t=1;
② P、Q都在AC上,此时P、Q重合,∴CP=6﹣t=3t﹣8,∴t=3.5;
③ P在BC上,Q在AC时,此时不存在;理由是:8÷3×1<6,Q到AC上时,P应也在AC上;
④ 当Q到A点(和A重合),P在BC上时,∵CQ=CP,CQ=AC=6,CP=t﹣6,∴t﹣6=6
∴t=12∵t<14∴t=12符合题意。答:点P运动1或3.5或12秒时,△PEC与△QFC全等.
8、我们把两组对边分别平行的四边形定义为平行四边形,同样的道理,我们也可以把至少有一组邻边相等的四边形定义为等邻边四边形.把对角互补的等邻边四边形定义为完美等邻边四边形.
(1)请写出一个你学过的特殊四边形中是等邻边四边形的图形的名称;
(2)已知,如图,完美等邻边四边形ABCD,AD=CD,∠B+∠D=180°,连接对角线AC,BD,请你结合图形,写出完美等邻边四边形的一条性质;
(3)在四边形ABCD中,若∠B+∠D=180°,且BD平分∠ABC时,求证:四边形ABCD是完美等邻边四边形.
【解答】解:(1)菱形、正方形都是满足条件的等邻边四边形
(2)性质是∠BAD+∠BCD=180°;
(3)证明:作DM⊥BC,DN⊥AB,垂足分别为M,N,∵BD平分∠ABC,DM⊥BC,DN⊥AB,∴DM=DN,
∵∠DMB=∠DNB=90°,∴∠ABC+∠MDN=180°,∵∠ABC+∠ADC=180°,∴∠ADC=∠MDN,∴∠ADN=∠MDC,
∵∠DNA=∠DMC,∴△DMC≌△DNA,∴AD=CD,∴四边形ABCD是等邻边四边形;
又∵∠ABC+∠ADC=180°,∴等邻边四边形ABCD是完美等邻边四边形.
9、如图①,在Rt△ABC中,∠C=90°,BC=9cm,AC=12cm,AB=15cm,现有一动点P,从点A出发,沿着三角形的边AC→CB→BA运动,回到点A停止,速度为3cm/s,设运动时间为ts.
(1)如图(1),当t= 或 时,△APC的面积等于△ABC面积的一半;
(2)如图(2),在△DEF中,∠E=90°,DE=4cm,DF=5cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边AB→BC→CA运动,回到点A停止.在两点运动过程中的某一时刻,恰好△APQ≌△DEF,求点Q的运动速度.
【解答】解:(1)① 当点P在BC上时,如图①﹣1,若△APC的面积等于△ABC面积的一半;则CP=BC=cm,
此时,点P移动的距离为AC+CP=12+=,移动的时间为:÷3=秒,
② 当点P在BA上时,如图①﹣2若△APC的面积等于△ABC面积的一半;则PD=BC,即点P为BA中点,
此时,点P移动的距离为AC+CB+BP=12+9+=cm,移动的时间为:÷3=秒,故答案为:或;
(2)△APQ≌△DEF,即,对应顶点为A与D,P与E,Q与F;
① 当点P在AC上,如图②﹣1所示:此时,AP=4,AQ=5,∴点Q移动的速度为5÷(4÷3)=cm/s,
② 当点P在AB上,如图②﹣2所示:此时,AP=4,AQ=5,即,点P移动的距离为9+12+15﹣4=32cm,
点Q移动的距离为9+12+15﹣5=31cm,∴点Q移动的速度为31÷(32÷3)=cm/s,
综上所述,两点运动过程中的某一时刻,恰好△APQ≌△DEF,点Q的运动速为cm/s或cm/s.
10、如图,在四边形ABCD中,∠B=∠C,AB=20cm.BC=15cm,点E为AB的中点,如果点P在线段BC上以5cm/秒的速度由点B向点C运动,同时,点Q在线段CD上由点C向点D运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPE与△CQP是否全等,请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPE与△CQP全等?
【解答】解:(1)△BPE与△CQP全等.
理由如下:∵点E为AB的中点,AB=20cm,∴BE=AB=×20=10cm,∵点P、Q的速度都是5cm/秒,
∴经过1秒后,BP=5cm,PC=BC﹣BP=15﹣5=10cm,CQ=5cm,∴BE=PC,BP=CQ,
在△BPE与△CQP中,,∴△BPE≌△CQP(SAS);
(2)∵△BPE与△CQP全等,∴CQ=BE=10,则PC=BP=7.5,点Q的运动速度为10÷(7.5÷5)=cm/秒;
或CP=BE=10,即BP=5,CQ=5,点Q的运动速度为5÷(5÷5)=5cm/秒;
∵点Q的运动速度与点P的运动速度不相等,∴x=5舍去,∴点Q的运动速度为cm/秒时,△BPE与△CQP全等.
1.4全等三角形
【知识点-部分】
要点一、全等图形:形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等图形.
要点诠释:一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.两个全等形的周长相等,面积相等。
要点二、全等三角形:能够完全重合的两个三角形叫全等三角形。
要点三、对应顶点,对应边,对应角
1、对应顶点,对应边,对应角定义:两个全等三角形重合在一起,
重合的顶点叫对应顶点,重合的边叫对应边,重合的角叫对应角.
要点诠释:
1、在写两个三角形全等时,通常把对应顶点的字母写在对应位置上,这样容易找出对应边、对应角.如下图,△ABC与△DEF全等,记作△ABC≌△DEF,其中点A和点D,点B和点E,点C和点F是对应顶点;AB和DE,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角。
2、找对应边、对应角的方法
(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;
(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角;
(3)有公共边的,公共边是对应边; (4)有公共角的,公共角是对应角;
(5)有对顶角的,对顶角一定是对应角;
(6)两个全等三角形中一对最长的边(或最大的角)是对应边(或角),一对最短的边(或最小的角)是对应边
(或角),等等。
要点四、全等三角形的性质
1、全等三角形的对应边相等; 2、全等三角形的对应角相等。
要点诠释:全等三角形对应边上的高相等,对应边上的中线相等,周长相等,面积相等.全等三角形的性质是今后研究其它全等图形的重要工具。
【典型例题-精选部分】
1、如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,
(1)当DE=8,BC=5时,线段AE的长为 ;
(2)已知∠D=35°,∠C=60°,① 求∠DBC的度数;② 求∠AFD的度数.
2、如图所示,D,A,E在同一条直线上,BD⊥DE于D,CE⊥DE于E,且△ABD≌△CAE,AD=2cm,BD=4cm,求
(1)DE的长; (2)∠BAC的度数.
3、如图,点A、B、C、D在同一条直线上,点E、F是直线.AD上方的点,连接AE、CE、BF、DF,
若△ACE≌△FDB,FD=3,AD=8.
(1)判断直线CE与DF是否平行?并说明理由; (2)求CD的长;
(3)若∠E=26°,∠F=53°,求∠ACE的度数.
4、如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P,若AD=DC=2.4,BC=4.1.
(1)若∠ABE=162°,∠DBC=30°,求∠CBE的度数; (2)求△DCP与△BPE的周长和.
5、如图,已知△ABF≌△ACF≌△DBF,∠FAB:∠ABF:∠AFB=4:7:25.
(1)求△ABF各内角的度数; (2)延长AF交BD于点G,求证:AG是△ABC的高;
(3)求∠CFD的度数; (4)求∠AED的度数.
6、如图,△ABE≌△EDC,E在BD上,AB⊥BD,B为垂足.
(1)试问:AE和CE垂直吗?AE和EC相等吗?
(2)分别将图中的△ABE绕点E按顺时针方向旋转,分别画出满足下列条件的图形并说出此时△ABE与△EDC中相等的边和角.① 使AE与CE重合;② 使AE与CE垂直;③ 使AE与EC在同一直线上.
7、如图,△ABC中,∠ACB=90°,AC=6,BC=8.点P从A点出发沿A﹣C﹣B路径向终点运动,终点为B点;点Q从B点出发沿B﹣C﹣A路径向终点运动,终点为A点.点P和Q分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.问:点P运动多少时间时,△PEC与△QFC全等?请说明理由.
8、我们把两组对边分别平行的四边形定义为平行四边形,同样的道理,我们也可以把至少有一组邻边相等的四边形定义为等邻边四边形.把对角互补的等邻边四边形定义为完美等邻边四边形.
(1)请写出一个你学过的特殊四边形中是等邻边四边形的图形的名称;
(2)已知,如图,完美等邻边四边形ABCD,AD=CD,∠B+∠D=180°,连接对角线AC,BD,请你结合图形,写出完美等邻边四边形的一条性质;
(3)在四边形ABCD中,若∠B+∠D=180°,且BD平分∠ABC时,求证:四边形ABCD是完美等邻边四边形.
9、如图①,在Rt△ABC中,∠C=90°,BC=9cm,AC=12cm,AB=15cm,现有一动点P,从点A出发,沿着三角形的边AC→CB→BA运动,回到点A停止,速度为3cm/s,设运动时间为ts.
(1)如图(1),当t= 时,△APC的面积等于△ABC面积的一半;
(2)如图(2),在△DEF中,∠E=90°,DE=4cm,DF=5cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边AB→BC→CA运动,回到点A停止.在两点运动过程中的某一时刻,恰好△APQ≌△DEF,求点Q的运动速度.
10、如图,在四边形ABCD中,∠B=∠C,AB=20cm.BC=15cm,点E为AB的中点,如果点P在线段BC上以5cm/秒的速度由点B向点C运动,同时,点Q在线段CD上由点C向点D运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPE与△CQP是否全等,请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPE与△CQP全等?
【参考答案】
1、如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,
(1)当DE=8,BC=5时,线段AE的长为 ;
(2)已知∠D=35°,∠C=60°,① 求∠DBC的度数;② 求∠AFD的度数.
【解答】解:(1)∵△ABC≌△DEB,DE=8,BC=5,∴AB=DE=8,BE=BC=5,∴AE=AB﹣BE=8﹣5=3;
(2)① ∵△ABC≌△DEB∴∠A=∠D=35°,∠DBE=∠C=60°,∵∠A+∠ABC+∠C=180°,
∴∠ABC=180°﹣∠A﹣∠C=85°,∴∠DBC=∠ABC﹣∠DBE=85°﹣60°=25°;
② ∵∠AEF是△DBE的外角,∴∠AEF=∠D+∠DBE=35°+60°=95°,
∵∠AFD是△AEF的外角,∴∠AFD=∠A+∠AEF=35°+95°=130°.
2、如图所示,D,A,E在同一条直线上,BD⊥DE于D,CE⊥DE于E,且△ABD≌△CAE,AD=2cm,BD=4cm,求
(1)DE的长; (2)∠BAC的度数.
【解答】解:(1)∵△ABD≌△CAE,AD=2cm,BD=4cm,∴AE=BD=4cm,∴DE=AD+AE=6cm;
(2)∵BD⊥DE,∴∠D=90°,∴∠DBA+∠BAD=90°,∵△ABD≌△CAE,
∴∠DBA=∠CAE∴∠BAD+∠CAE=90°,∴∠BAC=90°.
3、如图,点A、B、C、D在同一条直线上,点E、F是直线.AD上方的点,连接AE、CE、BF、DF,
若△ACE≌△FDB,FD=3,AD=8.
(1)判断直线CE与DF是否平行?并说明理由; (2)求CD的长;
(3)若∠E=26°,∠F=53°,求∠ACE的度数.
【解答】解:(1)CE∥DF, 理由:∵△ACE≌△FDB,∴∠ACE=∠D,∴CE∥DF;
(2)∵△ACE≌△FDB,∴AC=DF=3,∵AD=8,∴CD=AD﹣AC=8﹣3=5;
(3)∵△ACE≌△FDB,∴∠DBF=∠E=26°,∵CE∥DF,∴∠1=∠F=53°,∴∠ACE=180°﹣26°﹣53°=101°
4、如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P,若AD=DC=2.4,BC=4.1.
(1)若∠ABE=162°,∠DBC=30°,求∠CBE的度数; (2)求△DCP与△BPE的周长和.
【解答】解:(1)∵∠ABE=162°,∠DBC=30°,∴∠ABD+∠CBE=132°,∵△ABC≌△DBE,∴∠ABC=∠DBE,
∴∠ABD=∠CBE=132°÷2=66°,即∠CBE的度数为66°;
(2)∵△ABC≌△DBE,∴DE=AD+DC=4.8,BE=BC=4.1,
△DCP和△BPE的周长和=DC+DP+CP+BP+PE+BE=DC+DE+BC+BE=15.4.
5、如图,已知△ABF≌△ACF≌△DBF,∠FAB:∠ABF:∠AFB=4:7:25.
(1)求△ABF各内角的度数; (2)延长AF交BD于点G,求证:AG是△ABC的高;
(3)求∠CFD的度数; (4)求∠AED的度数.
【解答】解:(1)∵∠FAB:∠ABF:∠AFB=4:7:25,
∴∠FAB=180°×=20°,∠ABF=180°×=35°,∠AFB=180°×=125°;
(2)证明:∵△ABF≌△ACF,∴AB=AC,∠BAF=∠CAF,∴AG是等腰△ABC顶角的平分线,
∴AG是△ABC的高(等腰三角形三线合一);
(3)解:∵△ABF≌△ACF≌△DBF,∴∠AFC=∠BFD=∠AFB=125°,
∴∠AFE=360°﹣∠AFB﹣∠BFD=360°﹣125°﹣125°=110°,∴∠CFD=∠AFC﹣∠AFE=125°﹣110°=15°;
(4)解:∵△ABF≌△ACF,∴∠FAC=∠FAB=20°,
由三角形的外角性质得,∠AED=∠FAC+∠AFE=20°+110°=130°.
6、如图,△ABE≌△EDC,E在BD上,AB⊥BD,B为垂足.
(1)试问:AE和CE垂直吗?AE和EC相等吗?
(2)分别将图中的△ABE绕点E按顺时针方向旋转,分别画出满足下列条件的图形并说出此时△ABE与△EDC中相等的边和角.① 使AE与CE重合;② 使AE与CE垂直;③ 使AE与EC在同一直线上.
【解答】解:(1)∵△ABE≌△EDC,∴AE=EC,∠A=∠CED,∵AB⊥BD,∴∠A+∠AEB=90°,
∴∠CED+∠AEB=90°,∴∠AEC=180°﹣90°=90°,∴AE⊥CE;
(2)如图所示,相等的边有AB=ED,AE=EC,BE=DC,
相等的角有∠BAE=∠DEC,∠ABE=∠EDC,∠AEB=∠ECD.
7、如图,△ABC中,∠ACB=90°,AC=6,BC=8.点P从A点出发沿A﹣C﹣B路径向终点运动,终点为B点;点Q从B点出发沿B﹣C﹣A路径向终点运动,终点为A点.点P和Q分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.问:点P运动多少时间时,△PEC与△QFC全等?请说明理由.
【解答】解:设运动时间为t秒时,△PEC与△QFC全等,∵△PEC与△QFC全等,∴斜边CP=CQ,
有四种情况:① P在AC上,Q在BC上,CP=6﹣t,CQ=8﹣3t,∴6﹣t=8﹣3t,∴t=1;
② P、Q都在AC上,此时P、Q重合,∴CP=6﹣t=3t﹣8,∴t=3.5;
③ P在BC上,Q在AC时,此时不存在;理由是:8÷3×1<6,Q到AC上时,P应也在AC上;
④ 当Q到A点(和A重合),P在BC上时,∵CQ=CP,CQ=AC=6,CP=t﹣6,∴t﹣6=6
∴t=12∵t<14∴t=12符合题意。答:点P运动1或3.5或12秒时,△PEC与△QFC全等.
8、我们把两组对边分别平行的四边形定义为平行四边形,同样的道理,我们也可以把至少有一组邻边相等的四边形定义为等邻边四边形.把对角互补的等邻边四边形定义为完美等邻边四边形.
(1)请写出一个你学过的特殊四边形中是等邻边四边形的图形的名称;
(2)已知,如图,完美等邻边四边形ABCD,AD=CD,∠B+∠D=180°,连接对角线AC,BD,请你结合图形,写出完美等邻边四边形的一条性质;
(3)在四边形ABCD中,若∠B+∠D=180°,且BD平分∠ABC时,求证:四边形ABCD是完美等邻边四边形.
【解答】解:(1)菱形、正方形都是满足条件的等邻边四边形
(2)性质是∠BAD+∠BCD=180°;
(3)证明:作DM⊥BC,DN⊥AB,垂足分别为M,N,∵BD平分∠ABC,DM⊥BC,DN⊥AB,∴DM=DN,
∵∠DMB=∠DNB=90°,∴∠ABC+∠MDN=180°,∵∠ABC+∠ADC=180°,∴∠ADC=∠MDN,∴∠ADN=∠MDC,
∵∠DNA=∠DMC,∴△DMC≌△DNA,∴AD=CD,∴四边形ABCD是等邻边四边形;
又∵∠ABC+∠ADC=180°,∴等邻边四边形ABCD是完美等邻边四边形.
9、如图①,在Rt△ABC中,∠C=90°,BC=9cm,AC=12cm,AB=15cm,现有一动点P,从点A出发,沿着三角形的边AC→CB→BA运动,回到点A停止,速度为3cm/s,设运动时间为ts.
(1)如图(1),当t= 或 时,△APC的面积等于△ABC面积的一半;
(2)如图(2),在△DEF中,∠E=90°,DE=4cm,DF=5cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边AB→BC→CA运动,回到点A停止.在两点运动过程中的某一时刻,恰好△APQ≌△DEF,求点Q的运动速度.
【解答】解:(1)① 当点P在BC上时,如图①﹣1,若△APC的面积等于△ABC面积的一半;则CP=BC=cm,
此时,点P移动的距离为AC+CP=12+=,移动的时间为:÷3=秒,
② 当点P在BA上时,如图①﹣2若△APC的面积等于△ABC面积的一半;则PD=BC,即点P为BA中点,
此时,点P移动的距离为AC+CB+BP=12+9+=cm,移动的时间为:÷3=秒,故答案为:或;
(2)△APQ≌△DEF,即,对应顶点为A与D,P与E,Q与F;
① 当点P在AC上,如图②﹣1所示:此时,AP=4,AQ=5,∴点Q移动的速度为5÷(4÷3)=cm/s,
② 当点P在AB上,如图②﹣2所示:此时,AP=4,AQ=5,即,点P移动的距离为9+12+15﹣4=32cm,
点Q移动的距离为9+12+15﹣5=31cm,∴点Q移动的速度为31÷(32÷3)=cm/s,
综上所述,两点运动过程中的某一时刻,恰好△APQ≌△DEF,点Q的运动速为cm/s或cm/s.
10、如图,在四边形ABCD中,∠B=∠C,AB=20cm.BC=15cm,点E为AB的中点,如果点P在线段BC上以5cm/秒的速度由点B向点C运动,同时,点Q在线段CD上由点C向点D运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPE与△CQP是否全等,请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPE与△CQP全等?
【解答】解:(1)△BPE与△CQP全等.
理由如下:∵点E为AB的中点,AB=20cm,∴BE=AB=×20=10cm,∵点P、Q的速度都是5cm/秒,
∴经过1秒后,BP=5cm,PC=BC﹣BP=15﹣5=10cm,CQ=5cm,∴BE=PC,BP=CQ,
在△BPE与△CQP中,,∴△BPE≌△CQP(SAS);
(2)∵△BPE与△CQP全等,∴CQ=BE=10,则PC=BP=7.5,点Q的运动速度为10÷(7.5÷5)=cm/秒;
或CP=BE=10,即BP=5,CQ=5,点Q的运动速度为5÷(5÷5)=5cm/秒;
∵点Q的运动速度与点P的运动速度不相等,∴x=5舍去,∴点Q的运动速度为cm/秒时,△BPE与△CQP全等.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
