浙教版数学八年级上册1.1.4三角形角平分线和中垂线 同步练习(含答案)
文档属性
| 名称 | 浙教版数学八年级上册1.1.4三角形角平分线和中垂线 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 501.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-16 10:44:20 | ||
图片预览



文档简介
1.1.4三角形角平分线和中垂线同步练习
一、单选题
1.如图,CD是等腰三角形 △ABC底边上的中线,BE平分∠ABC,交CD于点E,AC=8,DE=2,则 △ BCE的面积是( )
A.4 B.6 C.8 D.12
2.如图,点P在锐角 的内部,连接 , ,点P关于 、 所在直线的对称点分别是 、 ,则 、 两点之间的距离可能是( )
A.8 B.7 C.6 D.5
3.如图, 平分 ,点P在 上,且 ,垂足为D,若 ,则P到 的距离d满足( )
A. B. C. D.无法确定
4.如图, 中, , , 的垂直平分线分别交 于点E,F,与 , 分别交于点D,G,则 的度数为( )
A. B. C. D.
5.如图,三条笔直的公路两两相交,交点分别在点A、B、C处,有两户村民分别在点D和点E处,现准备建造一个蓄水池,要求水池到两条公路AB、BC的距离相等,且到两户村民D、E的距离相等,则水池修建的位置应该是( )
A.在∠B的平分线与DE的交点处
B.在线段AB、AC的垂直平分线的交点处
C.在∠B的平分线与DE的垂直平分线的交点处
D.在∠A的平分线与DE的垂直平分线的交点处
6.如图,在等腰中,,,的平分线与AB的垂直平分线交于点E,沿FG折叠使点C与点E重合,则的度数是( ).
A.60度 B.55° C.50° D.45°
7.如图,任意画一个∠A=60°的△ABC,再分别作△ABC的两条角平分线BE和CD,BE和CD相交于点P,连接AP,有以下结论:①∠BPC=120°;②AP平分∠BAC;③点P到边AB,AC,BC的距离相等;④BD+CE=BC;⑤ ,其中错误的个数是( )个.
A.0 B.1 C.2 D.3
8.如图,在ABC中,∠C=90°,分别以A、B为圆心画弧,所画的弧交于两点,再连接该两点所在直线交BC于点D,连接AD.若BD=2,则AD的长为( )
A. B. C.1 D.2
9.如图,P是平分线上一点,OP=10,,在绕点P旋转的过程中始终保持不变,其两边和OA,OB分别相交于M,N,下列结论:①是等边三角形;②MN的值不变;③OM+ON=10;④四边形PMON面积不变.其中正确结论的个数为( )
A.4 B.3 C.2 D.1
二、填空题
10.如图,在∠AOB 的边 OA、OB 上取点 M、N,连接 MN,P 是△MON 外角平分线的交点, 若 MN=2,S△PMN=2,S△OMN=7.则△MON 的周长是 ;
11.如图,在 中, , 平分 , ,点D到 的距离为5.6,则 .
12.如图,已知∠BAC=130°,AB=AC,AC的垂直平分线交BC于点D,则∠BAD= ;
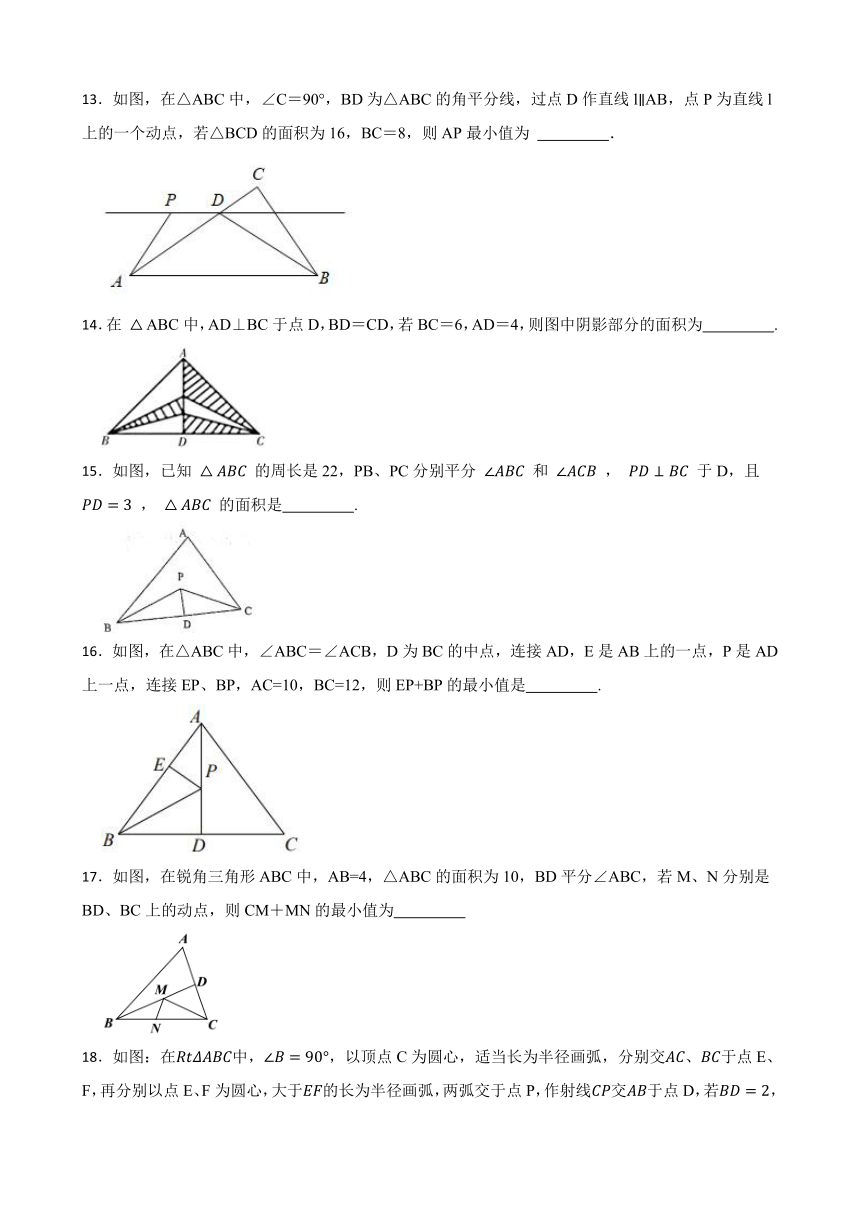
13.如图,在△ABC中,∠C=90°,BD为△ABC的角平分线,过点D作直线lAB,点P为直线l上的一个动点,若△BCD的面积为16,BC=8,则AP最小值为 .
14.在 ABC中,AD⊥BC于点D,BD=CD,若BC=6,AD=4,则图中阴影部分的面积为 .
15.如图,已知 的周长是22,PB、PC分别平分 和 , 于D,且 , 的面积是 .
16.如图,在△ABC中,∠ABC=∠ACB,D为BC的中点,连接AD,E是AB上的一点,P是AD上一点,连接EP、BP,AC=10,BC=12,则EP+BP的最小值是 .
17.如图,在锐角三角形ABC中,AB=4,△ABC的面积为10,BD平分∠ABC,若M、N分别是BD、BC上的动点,则CM+MN的最小值为
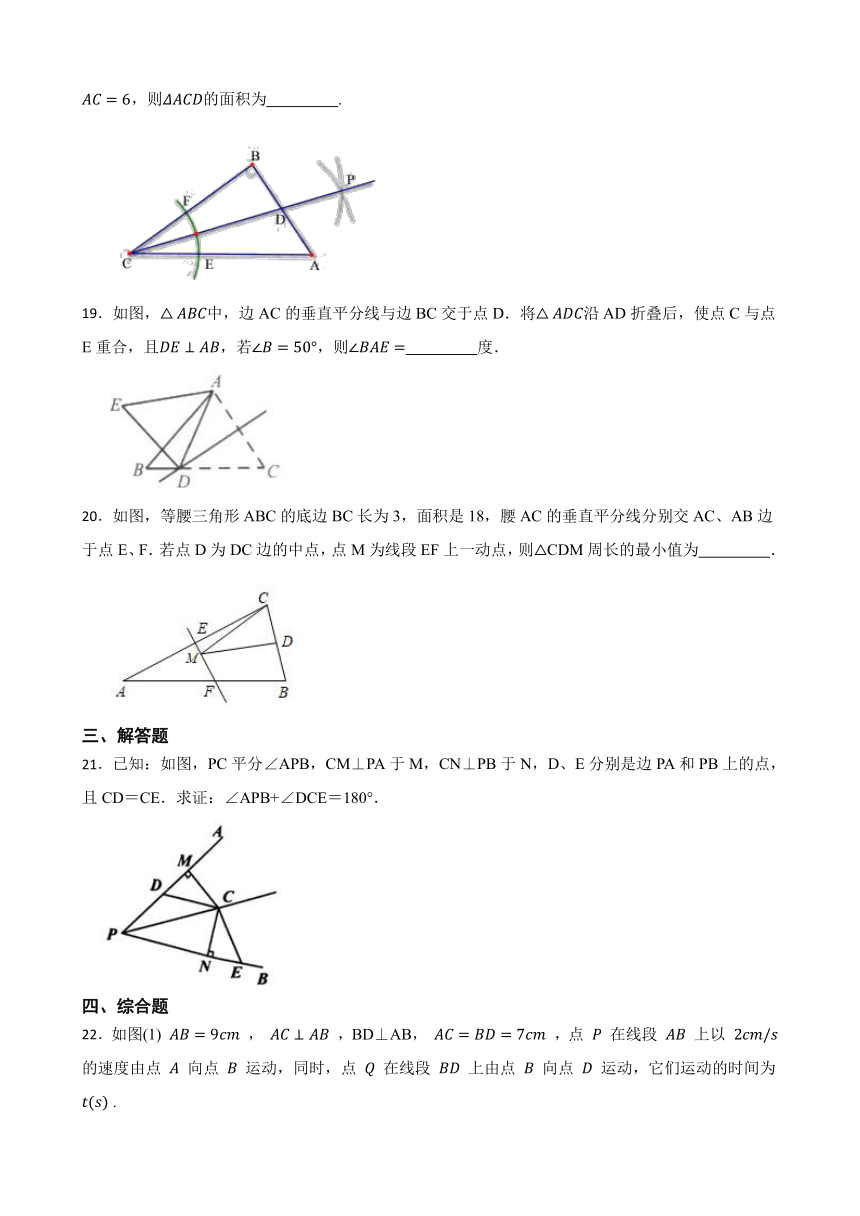
18.如图:在中,,以顶点C为圆心,适当长为半径画弧,分别交、于点E、F,再分别以点E、F为圆心,大于的长为半径画弧,两弧交于点P,作射线交于点D,若,,则的面积为 .
19.如图,中,边AC的垂直平分线与边BC交于点D.将沿AD折叠后,使点C与点E重合,且,若,则 度.
20.如图,等腰三角形ABC的底边BC长为3,面积是18,腰AC的垂直平分线分别交AC、AB边于点E、F.若点D为DC边的中点,点M为线段EF上一动点,则CDM周长的最小值为 .
三、解答题
21.已知:如图,PC平分∠APB,CM⊥PA于M,CN⊥PB于N,D、E分别是边PA和PB上的点,且CD=CE.求证:∠APB+∠DCE=180°.
四、综合题
22.如图(1) , ,BD⊥AB, ,点 在线段 上以 的速度由点 向点 运动,同时,点 在线段 上由点 向点 运动,它们运动的时间为 .
(1)若点 的速度与点 的速度相等,当 时,求证: ;
(2)在(1)的条件下,判断此时 和 的位置关系,并证明;
(3)将图(1)中的“ , ”,改为“ ”,得到图(2),其他条件不变.设点 的运动速度为 ,请问是否存在实数 ,使得 与 全等?若存在,求出相应的 和 的值;若不存在,请说明理由.
23.为培育学生“敢进取”精神,特设计此题:
如图1,在 中, ,AC=BC, , ,垂足分别为D,E.
(1)若AD=2.5cm,DE=1.7cm,求BE的长.
(2)如图2,在原题其他条件不变的前提下,将CE所在直线旋转到 ABC的外部,请你猜想AD,DE,BE三者之间的数量关系,直接写出结论: .(不需证明)
(3)如图3,若将原题中的条件改为:“在 ABC中,AC=BC,D,C,E三点在同一条直线上,并且有 ,其中 为任意钝角”,那么(2)中你的猜想是否还成立?若成立,请予以证明;若不成立,请说明理由.
24.已知:如图 ABC中,AB=AC=10,BC=8,∠A=39°,AB的垂直平分线MN交AC于D,交AB于M,连接BD.
求:
(1)∠DBC的度数;
(2)△BDC的周长.
25.在 中, , ,直线 经过点 ,且 于 , 于 .
(1)当直线 绕点 旋转到图1的位置时,
①求证: ≌ ;
②求证: ;
(2)当直线 绕点 旋转到图2的位置时,(1)中的结论②还成立吗?若成立,请给出证明;若不成立,说明理由.
26.下面是小东设计的尺规作图过程.
已知:如图,在Rt中,°.
求作:点,使得点在边上,且到和的距离相等.
作法:①如图,以点为圆心,任意长为半径画弧,分别交,于点,;
②分别以点,为圆心,大于为半径画弧,两弧交于点;
③画射线,交于点.
所以点即为所求.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:过点作于点,连接.
在和中,
∵,,,
∴≌(SSS).
∴∠ ▲ =∠ ▲ .
∵∠=90°,
∴.
∵,
∴( ▲ ).
27.如图,已知锐角.
(1)尺规作图:作的高(保留作图的痕迹,不要求写出作法);
(2)若,与有什么关系?并说明理由.
28.下面是小丽同学设计的“作30°角”的尺规作图过程.
已知:如图1,射线OA.
求作:∠AOB,使∠AOB =30°.
作法:如图2,
①在射线OA上任取一点C;
②分别以O,C为圆心,OC长为半径作弧,两弧在射线OA的上方交于点D,作射线OD,并连接CD;
③以O为圆心,任意长为半径作弧,分别交射线OA,OD于点E,F;
④分别以E,F为圆心,以大于的同样长为半径作弧,两弧在∠AOD内部交于点B;
⑤作射线OB;
∴ ∠AOB就是所求的角.
根据小丽设计的尺规作图过程,解答下列问题:
(1)使用直尺和圆规,依作法补全图2(保留作图痕迹);
(2)补全下面证明过程:
证明:连接BE,BF.
∵ OC=OD=CD,
∴ △OCD是等边三角形.
∴∠COD= ▲ °.
又∵ OE =OF,BE = BF,OB=OB,
∴ △OEB≌△OFB( ▲ )(填推理依据).
∴ ∠EOB=∠FOB( ▲ )(填推理依据).
∴ ∠AOB ==30°.
∴∠AOB就是所求的角.
29.如图,在 中, , 是 边的高.将 边对折,折痕为 ,连接 , 平分 .
(1)求 的度数.
(2)连接 ,求证: .
30.如图, , 于E, 交AD的延长线于F,且 .
(1)BE与DF是否相等?请说明理由;
(2)若 , ,则AB的长为 cm.
31.如图,在ΔABC中,AB、AC的垂直平分线l1、l2相交于点O.
(1)求证:点O在BC的垂直平分线上:
(2)若AB=AC=10,BC=12,则OA= .
32.下面是小军设计的“过线段端点作这条线段的垂线”的尺规作图过程.
已知:线段AB.
求作:AB的垂线,使它经过点A.
作法:如图,
①以点A为圆心,AB长为半径作弧,交线段BA的延长线于点C;
②分别以点B和点C为圆心,大于BC的长为半径作弧,两弧相交于直线BC上方的点D;
③作直线AD.
所以直线AD就是所求作的垂线.
根据小军设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接CD,BD.
∵BD= ▲ ,AB= ▲ ,
∴AD⊥AB( ▲ )(填推理的依据).
33.如图,在△ABC中,∠A=90°,BD平分∠ABC交AC于点D,AB=4,BC=12,AD=3,若点P在BC上运动.
(1)求线段DP的最小值;
(2)当DP最小时,求CDP的面积.
34.如图,OP是∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别为C,D.
(1)求证:OC=OD;
(2)求证:OP是CD的垂直平分线.
35.如图,在△ABC中,∠BAC=110°,分别交AB、BC于点D、E.MN垂直平分AC,分别交AC、BC于点M、N.连接AE、AN.
(1)求∠EAN的度数;
(2)若△AEN的周长为15,则BC的长为 .
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】B
4.【答案】A
5.【答案】C
6.【答案】C
7.【答案】A
8.【答案】D
9.【答案】B
10.【答案】11
11.【答案】16.8
12.【答案】105°
13.【答案】4
14.【答案】6
15.【答案】33
16.【答案】9.6
17.【答案】5
18.【答案】6
19.【答案】35
20.【答案】13.5
21.【答案】证明:∵PC平分∠APB,CM⊥PA于M,CN⊥PB于N,
∴CM=CN,∠PMC=90°,∠PNC=90°,
∴∠MPN+∠MCN=360°-∠PMC-∠PNC=360°-90°-90°=180°,
在Rt△MCD和Rt△NCE中,
,
∴Rt△MCD≌Rt△NCE(HL),
∴∠MCD=∠NCE,
∴∠APB+∠DCE=∠APB+∠DCN+∠NCE=∠APB+∠DCN+∠MCD=∠APB+∠MCN=180°.
22.【答案】(1)解: 与 全等,
理由如下:当 时, ,
则 ,
∴ ,
又∵ ,
在 和 中,
∴ ;
(2)解: ,
证明:∵ ,
∴ ,
∴ .
∴ ,
即 ;
(3)解: , ,
①若
则 , ,
∴ ,
解得: ,则 ;
②若 ,
则 , ,
则 ,解得, ,
∴ ,解得, ,
故当 , 或 , 时, 与 全等.
23.【答案】(1)解:∵ , ,
∴ ,
∴ .
∵ ,
∴ .
在 和 中,
,
,
∵DC=CE-DE,DE=1.7cm,
∴BE=0.8cm
(2)AD+BE=DE,(不需证明)
(3)(2)中的猜想还成立,
证明:∵ , , ,
∴
在 和 中,
,
,
∴ , ,
∴
24.【答案】(1)解:∵AB=AC,∠A=39°,
∴∠ABC=∠ACB=70.5°,
又∵DM为AB的垂直平分线,
∴DA=DB,
∴∠A=∠DBA=39°,
∴∠DBC=∠ABC-∠DBA=31.5°;
(2)解:∵DB=AD,AC=10,BC=8,
∴DB+DC=AD+DC=AC=10.
∴△DBC的周长为DB+DC+BC=18.
25.【答案】(1)证明:①∵AD⊥MN,BE⊥MN,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
又∵AC=BC,
∴ ≌ ;
②∵ ≌ ,
∴CD=BE,AD=CE,
∵DE=CE+CD,
∴DE=AD+BE;
(2)解:DE=AD+BE不成立,此时应有DE=AD-BE,理由如下:
∵BE⊥MN,AD⊥MN,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
又∵AC=BC,
∴ ≌ ,
∴AD=CE,CD=BE,
∵DE=CE-CD,
∴DE=AD-BE.
26.【答案】(1)解:补全的图形如下:
(2)解:过点作于点,连接.
在和中,
∵,,,
∴≌(SSS).
∴∠PAM=∠PAN.
∴=90°,
∴.
∵,
∴(角的平分线上的点到角的两边的距离相等).
故答案为:∠,∠,角的平分线上的点到角的两边的距离相等
27.【答案】(1)解:如图所示,即为所求;
(2)解:,理由如下:
在DC上截取DE=BD,连接AE,如图所示:
∵,
∴AB=AE,
∴∠B=∠AEB,
∵,
∴,
∵,
∴,
∴AE=EC=AB,
∵,
∴.
28.【答案】(1)解:补全作图如下,
(2)证明:连接BE,BF.
∵ OC=OD=CD,
∴ △OCD是等边三角形.
∴∠COD=60°.
又∵ OE =OF,BE = BF,OB=OB,
∴ △OEB≌△OFB(SSS)(填推理依据).
∴ ∠EOB=∠FOB(全等三角形对应角相等)(填推理依据).
∴ ∠AOB ==30°.
∴∠AOB就是所求的角.
故答案为:60°,SSS,全等三角形对应角相等
29.【答案】(1)解: 是 的对称轴,
, ,
.
是 边的高,
.
平分 ,
.
又 ,
.
.
, .
.
,
,
,
.
(2)证明:
, ,
, .
是等边三角形.
.
.
30.【答案】(1)解:BE=DF,理由是:
∵∠1=∠2,CE⊥AB于E,CF⊥AD于F,
∴CE=CF,∠F=∠CEB=90°,
在Rt△CEB和Rt△CFD中,
∴ ,
∴BE=DF;
(2)5
31.【答案】(1)证明:连接AO,
∵l1是AB的垂直平分线,
∴AO=BO,
∵l2是AC的垂直平分线,
∴AO=CO,
∴BO=CO,
∴点O在BC的垂直平分线上.
(2)
32.【答案】(1)解:补全的图形如图所示:
(2)证明:连接CD,BD.
∵BD=CD,AB=AC ,
∴AD⊥AB(等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合)(填推理的依据).
故答案为:CD,AC,等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合
33.【答案】(1)解:当DP⊥BC时,线段DP的值最小,
∵BD平分∠ABC,∠A=90°,
当DP⊥BC时,DP=AD,
∵AD=3,
∴DP的最小值是3;
(2)解:∵∠A=90°,
∴BD==5,
当DP最小时,DP=3,DP⊥BC,
则∠DPB=∠DPC=90°,
∴PB==4,
∴CP=BC-PB=12-4=8,
∴△CDP的面积=CP×DP=×8×3=12,
即当DP最小时,△CDP的面积为12.
34.【答案】(1)证明:∵P是∠AOB平分线上的一点,PC⊥OA,PD⊥OB,
∴PC=PD,
在Rt△POC与Rt△POD中,
∵,
∴Rt△POC≌Rt△POD(HL),
∴OC=OD;
(2)证明:
∵P是∠AOB平分线上的一点,
∴∠COP=∠DOP ,
∵由(1)知,OC=OD,
∴在△COE与△DOE中,
,
∴△COE≌△DOE(SAS),
∴CE=DE,∠CEO=∠DEO ,
∵∠CEO+∠DEO =180°,
∴∠CEO=∠DEO= 90°,
∴OE⊥CD,
∴OP是CD的垂直平分线.
35.【答案】(1)解:∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,同理可得∠CAN=∠C,
∴∠EAN=∠BAC-∠BAE-∠CAN=∠BAC-(∠B+∠C),
在△ABC中,∠B+∠C=180°-∠BAC=70°,
∴∠EAN=110°-70°=40°;
(2)15
一、单选题
1.如图,CD是等腰三角形 △ABC底边上的中线,BE平分∠ABC,交CD于点E,AC=8,DE=2,则 △ BCE的面积是( )
A.4 B.6 C.8 D.12
2.如图,点P在锐角 的内部,连接 , ,点P关于 、 所在直线的对称点分别是 、 ,则 、 两点之间的距离可能是( )
A.8 B.7 C.6 D.5
3.如图, 平分 ,点P在 上,且 ,垂足为D,若 ,则P到 的距离d满足( )
A. B. C. D.无法确定
4.如图, 中, , , 的垂直平分线分别交 于点E,F,与 , 分别交于点D,G,则 的度数为( )
A. B. C. D.
5.如图,三条笔直的公路两两相交,交点分别在点A、B、C处,有两户村民分别在点D和点E处,现准备建造一个蓄水池,要求水池到两条公路AB、BC的距离相等,且到两户村民D、E的距离相等,则水池修建的位置应该是( )
A.在∠B的平分线与DE的交点处
B.在线段AB、AC的垂直平分线的交点处
C.在∠B的平分线与DE的垂直平分线的交点处
D.在∠A的平分线与DE的垂直平分线的交点处
6.如图,在等腰中,,,的平分线与AB的垂直平分线交于点E,沿FG折叠使点C与点E重合,则的度数是( ).
A.60度 B.55° C.50° D.45°
7.如图,任意画一个∠A=60°的△ABC,再分别作△ABC的两条角平分线BE和CD,BE和CD相交于点P,连接AP,有以下结论:①∠BPC=120°;②AP平分∠BAC;③点P到边AB,AC,BC的距离相等;④BD+CE=BC;⑤ ,其中错误的个数是( )个.
A.0 B.1 C.2 D.3
8.如图,在ABC中,∠C=90°,分别以A、B为圆心画弧,所画的弧交于两点,再连接该两点所在直线交BC于点D,连接AD.若BD=2,则AD的长为( )
A. B. C.1 D.2
9.如图,P是平分线上一点,OP=10,,在绕点P旋转的过程中始终保持不变,其两边和OA,OB分别相交于M,N,下列结论:①是等边三角形;②MN的值不变;③OM+ON=10;④四边形PMON面积不变.其中正确结论的个数为( )
A.4 B.3 C.2 D.1
二、填空题
10.如图,在∠AOB 的边 OA、OB 上取点 M、N,连接 MN,P 是△MON 外角平分线的交点, 若 MN=2,S△PMN=2,S△OMN=7.则△MON 的周长是 ;
11.如图,在 中, , 平分 , ,点D到 的距离为5.6,则 .
12.如图,已知∠BAC=130°,AB=AC,AC的垂直平分线交BC于点D,则∠BAD= ;
13.如图,在△ABC中,∠C=90°,BD为△ABC的角平分线,过点D作直线lAB,点P为直线l上的一个动点,若△BCD的面积为16,BC=8,则AP最小值为 .
14.在 ABC中,AD⊥BC于点D,BD=CD,若BC=6,AD=4,则图中阴影部分的面积为 .
15.如图,已知 的周长是22,PB、PC分别平分 和 , 于D,且 , 的面积是 .
16.如图,在△ABC中,∠ABC=∠ACB,D为BC的中点,连接AD,E是AB上的一点,P是AD上一点,连接EP、BP,AC=10,BC=12,则EP+BP的最小值是 .
17.如图,在锐角三角形ABC中,AB=4,△ABC的面积为10,BD平分∠ABC,若M、N分别是BD、BC上的动点,则CM+MN的最小值为
18.如图:在中,,以顶点C为圆心,适当长为半径画弧,分别交、于点E、F,再分别以点E、F为圆心,大于的长为半径画弧,两弧交于点P,作射线交于点D,若,,则的面积为 .
19.如图,中,边AC的垂直平分线与边BC交于点D.将沿AD折叠后,使点C与点E重合,且,若,则 度.
20.如图,等腰三角形ABC的底边BC长为3,面积是18,腰AC的垂直平分线分别交AC、AB边于点E、F.若点D为DC边的中点,点M为线段EF上一动点,则CDM周长的最小值为 .
三、解答题
21.已知:如图,PC平分∠APB,CM⊥PA于M,CN⊥PB于N,D、E分别是边PA和PB上的点,且CD=CE.求证:∠APB+∠DCE=180°.
四、综合题
22.如图(1) , ,BD⊥AB, ,点 在线段 上以 的速度由点 向点 运动,同时,点 在线段 上由点 向点 运动,它们运动的时间为 .
(1)若点 的速度与点 的速度相等,当 时,求证: ;
(2)在(1)的条件下,判断此时 和 的位置关系,并证明;
(3)将图(1)中的“ , ”,改为“ ”,得到图(2),其他条件不变.设点 的运动速度为 ,请问是否存在实数 ,使得 与 全等?若存在,求出相应的 和 的值;若不存在,请说明理由.
23.为培育学生“敢进取”精神,特设计此题:
如图1,在 中, ,AC=BC, , ,垂足分别为D,E.
(1)若AD=2.5cm,DE=1.7cm,求BE的长.
(2)如图2,在原题其他条件不变的前提下,将CE所在直线旋转到 ABC的外部,请你猜想AD,DE,BE三者之间的数量关系,直接写出结论: .(不需证明)
(3)如图3,若将原题中的条件改为:“在 ABC中,AC=BC,D,C,E三点在同一条直线上,并且有 ,其中 为任意钝角”,那么(2)中你的猜想是否还成立?若成立,请予以证明;若不成立,请说明理由.
24.已知:如图 ABC中,AB=AC=10,BC=8,∠A=39°,AB的垂直平分线MN交AC于D,交AB于M,连接BD.
求:
(1)∠DBC的度数;
(2)△BDC的周长.
25.在 中, , ,直线 经过点 ,且 于 , 于 .
(1)当直线 绕点 旋转到图1的位置时,
①求证: ≌ ;
②求证: ;
(2)当直线 绕点 旋转到图2的位置时,(1)中的结论②还成立吗?若成立,请给出证明;若不成立,说明理由.
26.下面是小东设计的尺规作图过程.
已知:如图,在Rt中,°.
求作:点,使得点在边上,且到和的距离相等.
作法:①如图,以点为圆心,任意长为半径画弧,分别交,于点,;
②分别以点,为圆心,大于为半径画弧,两弧交于点;
③画射线,交于点.
所以点即为所求.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:过点作于点,连接.
在和中,
∵,,,
∴≌(SSS).
∴∠ ▲ =∠ ▲ .
∵∠=90°,
∴.
∵,
∴( ▲ ).
27.如图,已知锐角.
(1)尺规作图:作的高(保留作图的痕迹,不要求写出作法);
(2)若,与有什么关系?并说明理由.
28.下面是小丽同学设计的“作30°角”的尺规作图过程.
已知:如图1,射线OA.
求作:∠AOB,使∠AOB =30°.
作法:如图2,
①在射线OA上任取一点C;
②分别以O,C为圆心,OC长为半径作弧,两弧在射线OA的上方交于点D,作射线OD,并连接CD;
③以O为圆心,任意长为半径作弧,分别交射线OA,OD于点E,F;
④分别以E,F为圆心,以大于的同样长为半径作弧,两弧在∠AOD内部交于点B;
⑤作射线OB;
∴ ∠AOB就是所求的角.
根据小丽设计的尺规作图过程,解答下列问题:
(1)使用直尺和圆规,依作法补全图2(保留作图痕迹);
(2)补全下面证明过程:
证明:连接BE,BF.
∵ OC=OD=CD,
∴ △OCD是等边三角形.
∴∠COD= ▲ °.
又∵ OE =OF,BE = BF,OB=OB,
∴ △OEB≌△OFB( ▲ )(填推理依据).
∴ ∠EOB=∠FOB( ▲ )(填推理依据).
∴ ∠AOB ==30°.
∴∠AOB就是所求的角.
29.如图,在 中, , 是 边的高.将 边对折,折痕为 ,连接 , 平分 .
(1)求 的度数.
(2)连接 ,求证: .
30.如图, , 于E, 交AD的延长线于F,且 .
(1)BE与DF是否相等?请说明理由;
(2)若 , ,则AB的长为 cm.
31.如图,在ΔABC中,AB、AC的垂直平分线l1、l2相交于点O.
(1)求证:点O在BC的垂直平分线上:
(2)若AB=AC=10,BC=12,则OA= .
32.下面是小军设计的“过线段端点作这条线段的垂线”的尺规作图过程.
已知:线段AB.
求作:AB的垂线,使它经过点A.
作法:如图,
①以点A为圆心,AB长为半径作弧,交线段BA的延长线于点C;
②分别以点B和点C为圆心,大于BC的长为半径作弧,两弧相交于直线BC上方的点D;
③作直线AD.
所以直线AD就是所求作的垂线.
根据小军设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接CD,BD.
∵BD= ▲ ,AB= ▲ ,
∴AD⊥AB( ▲ )(填推理的依据).
33.如图,在△ABC中,∠A=90°,BD平分∠ABC交AC于点D,AB=4,BC=12,AD=3,若点P在BC上运动.
(1)求线段DP的最小值;
(2)当DP最小时,求CDP的面积.
34.如图,OP是∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别为C,D.
(1)求证:OC=OD;
(2)求证:OP是CD的垂直平分线.
35.如图,在△ABC中,∠BAC=110°,分别交AB、BC于点D、E.MN垂直平分AC,分别交AC、BC于点M、N.连接AE、AN.
(1)求∠EAN的度数;
(2)若△AEN的周长为15,则BC的长为 .
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】B
4.【答案】A
5.【答案】C
6.【答案】C
7.【答案】A
8.【答案】D
9.【答案】B
10.【答案】11
11.【答案】16.8
12.【答案】105°
13.【答案】4
14.【答案】6
15.【答案】33
16.【答案】9.6
17.【答案】5
18.【答案】6
19.【答案】35
20.【答案】13.5
21.【答案】证明:∵PC平分∠APB,CM⊥PA于M,CN⊥PB于N,
∴CM=CN,∠PMC=90°,∠PNC=90°,
∴∠MPN+∠MCN=360°-∠PMC-∠PNC=360°-90°-90°=180°,
在Rt△MCD和Rt△NCE中,
,
∴Rt△MCD≌Rt△NCE(HL),
∴∠MCD=∠NCE,
∴∠APB+∠DCE=∠APB+∠DCN+∠NCE=∠APB+∠DCN+∠MCD=∠APB+∠MCN=180°.
22.【答案】(1)解: 与 全等,
理由如下:当 时, ,
则 ,
∴ ,
又∵ ,
在 和 中,
∴ ;
(2)解: ,
证明:∵ ,
∴ ,
∴ .
∴ ,
即 ;
(3)解: , ,
①若
则 , ,
∴ ,
解得: ,则 ;
②若 ,
则 , ,
则 ,解得, ,
∴ ,解得, ,
故当 , 或 , 时, 与 全等.
23.【答案】(1)解:∵ , ,
∴ ,
∴ .
∵ ,
∴ .
在 和 中,
,
,
∵DC=CE-DE,DE=1.7cm,
∴BE=0.8cm
(2)AD+BE=DE,(不需证明)
(3)(2)中的猜想还成立,
证明:∵ , , ,
∴
在 和 中,
,
,
∴ , ,
∴
24.【答案】(1)解:∵AB=AC,∠A=39°,
∴∠ABC=∠ACB=70.5°,
又∵DM为AB的垂直平分线,
∴DA=DB,
∴∠A=∠DBA=39°,
∴∠DBC=∠ABC-∠DBA=31.5°;
(2)解:∵DB=AD,AC=10,BC=8,
∴DB+DC=AD+DC=AC=10.
∴△DBC的周长为DB+DC+BC=18.
25.【答案】(1)证明:①∵AD⊥MN,BE⊥MN,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
又∵AC=BC,
∴ ≌ ;
②∵ ≌ ,
∴CD=BE,AD=CE,
∵DE=CE+CD,
∴DE=AD+BE;
(2)解:DE=AD+BE不成立,此时应有DE=AD-BE,理由如下:
∵BE⊥MN,AD⊥MN,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
又∵AC=BC,
∴ ≌ ,
∴AD=CE,CD=BE,
∵DE=CE-CD,
∴DE=AD-BE.
26.【答案】(1)解:补全的图形如下:
(2)解:过点作于点,连接.
在和中,
∵,,,
∴≌(SSS).
∴∠PAM=∠PAN.
∴=90°,
∴.
∵,
∴(角的平分线上的点到角的两边的距离相等).
故答案为:∠,∠,角的平分线上的点到角的两边的距离相等
27.【答案】(1)解:如图所示,即为所求;
(2)解:,理由如下:
在DC上截取DE=BD,连接AE,如图所示:
∵,
∴AB=AE,
∴∠B=∠AEB,
∵,
∴,
∵,
∴,
∴AE=EC=AB,
∵,
∴.
28.【答案】(1)解:补全作图如下,
(2)证明:连接BE,BF.
∵ OC=OD=CD,
∴ △OCD是等边三角形.
∴∠COD=60°.
又∵ OE =OF,BE = BF,OB=OB,
∴ △OEB≌△OFB(SSS)(填推理依据).
∴ ∠EOB=∠FOB(全等三角形对应角相等)(填推理依据).
∴ ∠AOB ==30°.
∴∠AOB就是所求的角.
故答案为:60°,SSS,全等三角形对应角相等
29.【答案】(1)解: 是 的对称轴,
, ,
.
是 边的高,
.
平分 ,
.
又 ,
.
.
, .
.
,
,
,
.
(2)证明:
, ,
, .
是等边三角形.
.
.
30.【答案】(1)解:BE=DF,理由是:
∵∠1=∠2,CE⊥AB于E,CF⊥AD于F,
∴CE=CF,∠F=∠CEB=90°,
在Rt△CEB和Rt△CFD中,
∴ ,
∴BE=DF;
(2)5
31.【答案】(1)证明:连接AO,
∵l1是AB的垂直平分线,
∴AO=BO,
∵l2是AC的垂直平分线,
∴AO=CO,
∴BO=CO,
∴点O在BC的垂直平分线上.
(2)
32.【答案】(1)解:补全的图形如图所示:
(2)证明:连接CD,BD.
∵BD=CD,AB=AC ,
∴AD⊥AB(等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合)(填推理的依据).
故答案为:CD,AC,等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合
33.【答案】(1)解:当DP⊥BC时,线段DP的值最小,
∵BD平分∠ABC,∠A=90°,
当DP⊥BC时,DP=AD,
∵AD=3,
∴DP的最小值是3;
(2)解:∵∠A=90°,
∴BD==5,
当DP最小时,DP=3,DP⊥BC,
则∠DPB=∠DPC=90°,
∴PB==4,
∴CP=BC-PB=12-4=8,
∴△CDP的面积=CP×DP=×8×3=12,
即当DP最小时,△CDP的面积为12.
34.【答案】(1)证明:∵P是∠AOB平分线上的一点,PC⊥OA,PD⊥OB,
∴PC=PD,
在Rt△POC与Rt△POD中,
∵,
∴Rt△POC≌Rt△POD(HL),
∴OC=OD;
(2)证明:
∵P是∠AOB平分线上的一点,
∴∠COP=∠DOP ,
∵由(1)知,OC=OD,
∴在△COE与△DOE中,
,
∴△COE≌△DOE(SAS),
∴CE=DE,∠CEO=∠DEO ,
∵∠CEO+∠DEO =180°,
∴∠CEO=∠DEO= 90°,
∴OE⊥CD,
∴OP是CD的垂直平分线.
35.【答案】(1)解:∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,同理可得∠CAN=∠C,
∴∠EAN=∠BAC-∠BAE-∠CAN=∠BAC-(∠B+∠C),
在△ABC中,∠B+∠C=180°-∠BAC=70°,
∴∠EAN=110°-70°=40°;
(2)15
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
