浙教版八年级上册数学 1.5全等三角形判定 提高练习(含答案)
文档属性
| 名称 | 浙教版八年级上册数学 1.5全等三角形判定 提高练习(含答案) | 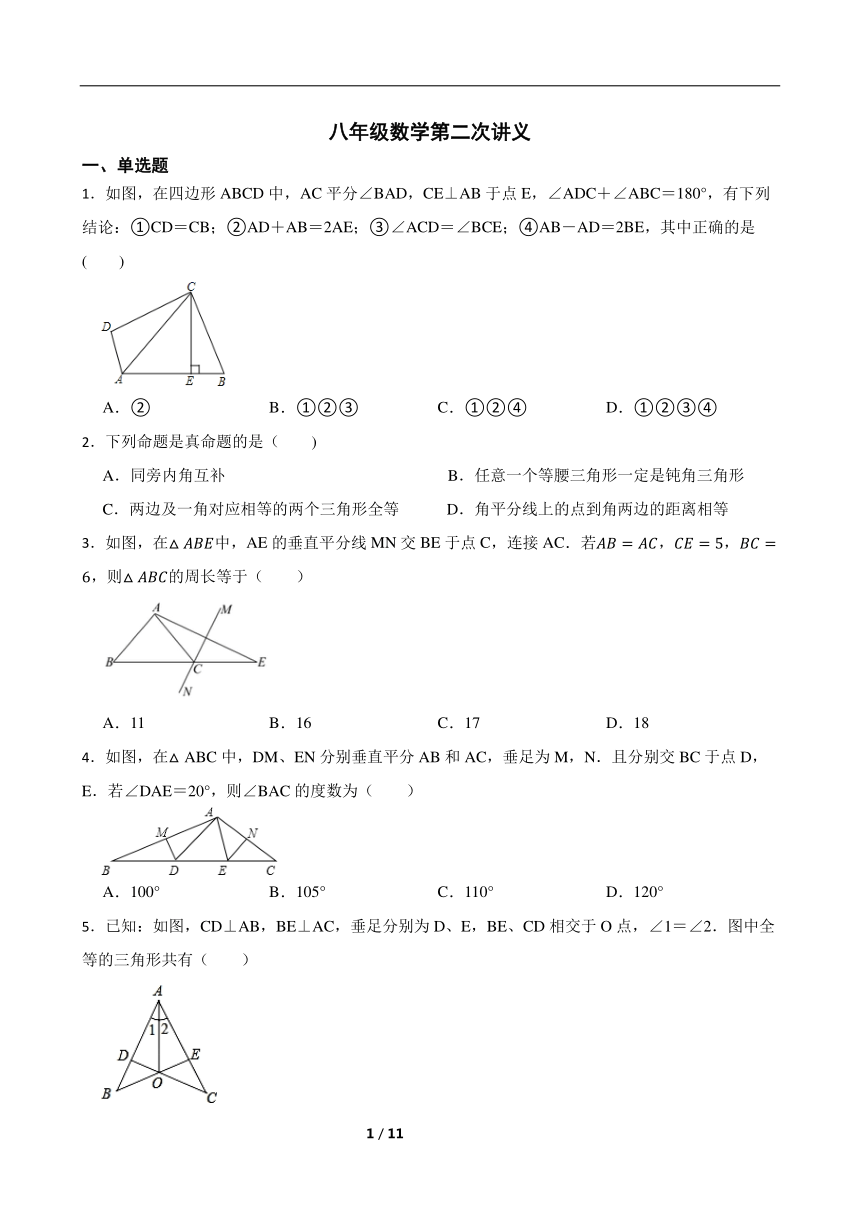 | |
| 格式 | zip | ||
| 文件大小 | 189.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-17 15:52:10 | ||
图片预览



文档简介
八年级数学第二次讲义
一、单选题
1.如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,∠ADC+∠ABC=180°,有下列结论:①CD=CB;②AD+AB=2AE;③∠ACD=∠BCE;④AB-AD=2BE,其中正确的是( )
A.② B.①②③ C.①②④ D.①②③④
2.下列命题是真命题的是( )
A.同旁内角互补 B.任意一个等腰三角形一定是钝角三角形
C.两边及一角对应相等的两个三角形全等 D.角平分线上的点到角两边的距离相等
3.如图,在中,AE的垂直平分线MN交BE于点C,连接AC.若,,,则的周长等于( )
A.11 B.16 C.17 D.18
4.如图,在△ABC中,DM、EN分别垂直平分AB和AC,垂足为M,N.且分别交BC于点D,E.若∠DAE=20°,则∠BAC的度数为( )
A.100° B.105° C.110° D.120°
5.已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2.图中全等的三角形共有( )
A.4对 B.3对 C.2对 D.1对
6.如图所示,∠B=∠C=90°,E是BC的中点,AE平分∠DAB,则下列说法正确的个数是( )
⑴DE平分∠CDA;⑵△EBA≌△EDA;⑶△EBA≌△DCE;⑷AB+CD=AD;⑸AE2+DE2=AD2
A.4个 B.3个 C.2个 D.1个
二、填空题
7.在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=2cm,过点E作EF⊥AC交CD的延长线于点F.若AE=3cm,则EF= cm.
8.如图,△ABC是等边三角形.在AC,BC边上各取一点P,Q,使 AP=CQ,且∠ABP=20°,AQ,BP相交于点O,则∠AQB= .
9.如图,线段AB、BC的垂直平分线l1、l2相交于点O,若∠1=37°,则∠AOC= .
10.如图,在锐角三角形ABC中,AB=4,△ABC的面积为10,BD平分∠ABC,若M、N分别是BD、BC上的动点,则CM+MN的最小值为
11.如图,在△ABC中,∠C=90°,BD为△ABC的角平分线,过点D作直线lAB,点P为直线l上的一个动点,若△BCD的面积为16,BC=8,则AP最小值为 .
12.如图,在△ABC中,BD、CE是△ABC的角平分线,BD,CE交于点O.过点O作OF⊥BC,垂足为F,若∠BAC=120°,OD OE=12,BC BE CD=5,则OF= .
三、综合题
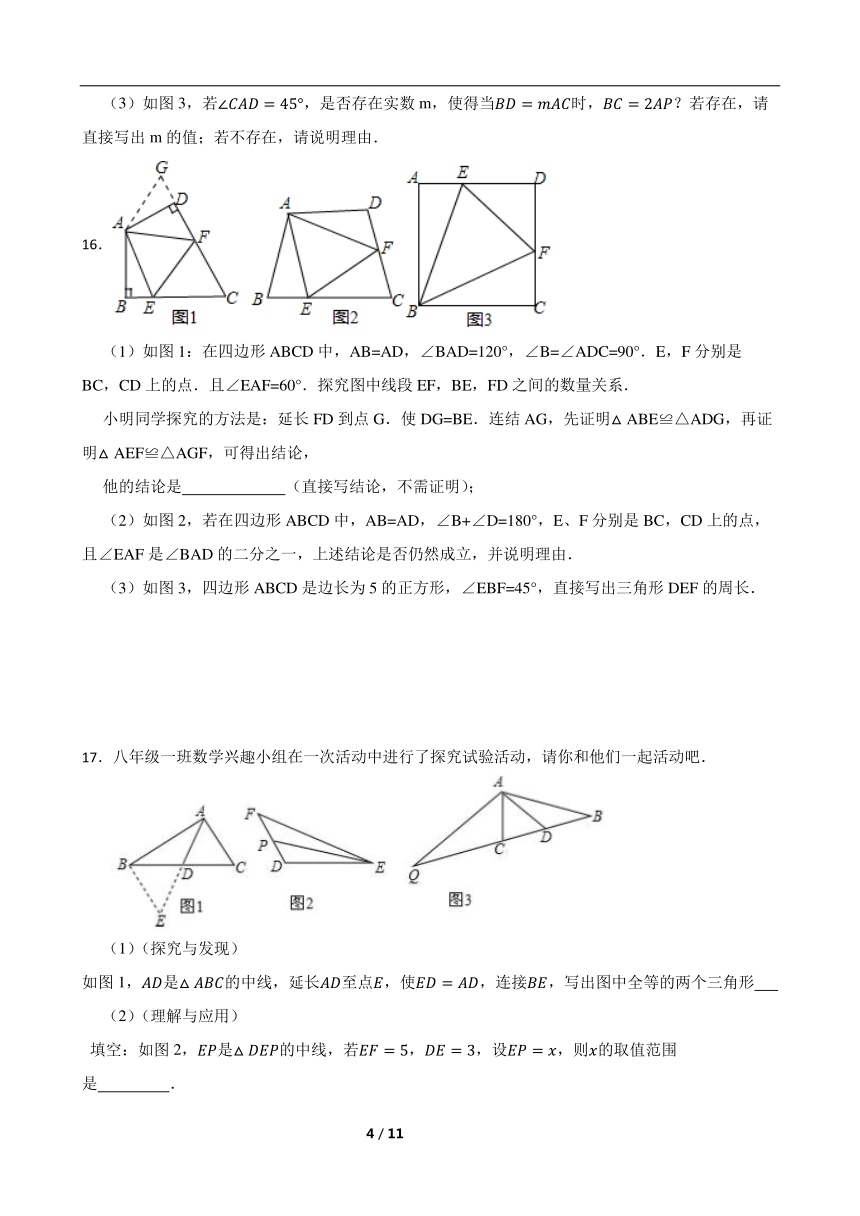
13.如图,在 中,已知 的垂直平分线交 于点N,交 于点M,连接 .
(1)若 ,求 的度数.
(2)若 , 的周长是 .
①求 的长度;
②若点P为直线 上一点,请你求出 周长的最小值.
14.如图,在 中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G,交AB于点E,连接EG、EF.
(1)求证: .
(2)请你判断: 与EF的大小关系,并加以证明.
15.已知在中,P是的中点,B是延长线上的一点,连接,.
(1)如图1,若,,,,求的长;
(2)过点D作,交的延长线于点E,如图2所示,若,,求证:;
(3)如图3,若,是否存在实数m,使得当时,?若存在,请直接写出m的值;若不存在,请说明理由.
16.
(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段EF,BE,FD之间的数量关系.
小明同学探究的方法是:延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,
他的结论是 (直接写结论,不需证明);
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC,CD上的点,且∠EAF是∠BAD的二分之一,上述结论是否仍然成立,并说明理由.
(3)如图3,四边形ABCD是边长为5的正方形,∠EBF=45°,直接写出三角形DEF的周长.
17.八年级一班数学兴趣小组在一次活动中进行了探究试验活动,请你和他们一起活动吧.
(1)(探究与发现)
如图1,是的中线,延长至点,使,连接,写出图中全等的两个三角形
(2)(理解与应用)
填空:如图2,是的中线,若,,设,则的取值范围是 .
(3)已知:如图3,是的中线,,点在的延长线上,,求证:.
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】B
4.【答案】A
5.【答案】A
6.【答案】B
7.【答案】5
8.【答案】80°
9.【答案】76°
10.【答案】5
11.【答案】4
12.【答案】
13.【答案】(1)解:∵ ,
∴ ,
∴ ,
∵ 的垂直平分线交 于点N,
∴ ,
∴
(2)解:①∵ 是 的垂直平分线,
∴ ,
∴ 的周长 ,
∵ , 的周长是 ,
∴ ;
② 周长 最小,即 最小,
根据轴对称性质得,当点P与M重合时,即 最小,
此时 周长的值最小,
∴ 周长的最小值
14.【答案】(1)证明:∵BG∥AC,
∴ ,
∵D是BC的中点,
∴BD=DC,
在△BDG和△CDF中,
,
∴ ,
∴ ;
(2)解: ,
由 得 ,
∵ ,∴ ,
∵ ,∴ ,
∴ .
15.【答案】(1)解:∵,,
∴∠B=180°-∠CAB-∠ACB=180°-90°-60°=30°,
∴,
∵,
∴,
∴是等边三角形,
∴.
∵P是的中点,
∴.
在中,,
设,则,
∴,
∴,
∴(已舍去),
∴.
(2)证明:如图1,连接,
∵DE∥AC,
∴.
在和中,
,
∴△CPA≌△DPE(AAS),
∴,.
∵,
∴.
又∵DE∥AC,
∴,
∴是等边三角形,
∴,.
∵,
∴.
在△CAB和△EBA中,
,
∴△CAB≌△EBA(SAS),
∴,
∴.
(3)解:存在这样的m,m=.
16.【答案】(1)EF=BE+DF
(2)结论EF=BE+DF仍然成立;
理由:如图2,延长FD到点G.使DG=BE.连结AG
在△ABE和△ADG中,
∵,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
∵,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
(3)解:如图3,延长DC到点G,截取CG=AE,连接BG,
在△AEB与△CGB中,
∵
,
∴△AEB≌△CGB(SAS),
∴BE=BG,∠ABE=∠CBG.
∵∠EBF=45°,∠ABC=90°,
∴∠ABE+∠CBF=45°,
∴∠CBF+∠CBG=45°.
在△EBF与△GBF中,
∵,
∴△EBF≌△GBF(SAS),
∴EF=GF,
∴△DEF的周长=EF+ED+CF=AE+CF+DE+DF=AD+CD=10.
17.【答案】(1)
(2)
(3)证明:如图3,延长到,使,连接,
,
是的中线,
,
在与中,
,
,
,,
,
,,
,,
,
,
,
在与中,
,
,
.
1 / 1
一、单选题
1.如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,∠ADC+∠ABC=180°,有下列结论:①CD=CB;②AD+AB=2AE;③∠ACD=∠BCE;④AB-AD=2BE,其中正确的是( )
A.② B.①②③ C.①②④ D.①②③④
2.下列命题是真命题的是( )
A.同旁内角互补 B.任意一个等腰三角形一定是钝角三角形
C.两边及一角对应相等的两个三角形全等 D.角平分线上的点到角两边的距离相等
3.如图,在中,AE的垂直平分线MN交BE于点C,连接AC.若,,,则的周长等于( )
A.11 B.16 C.17 D.18
4.如图,在△ABC中,DM、EN分别垂直平分AB和AC,垂足为M,N.且分别交BC于点D,E.若∠DAE=20°,则∠BAC的度数为( )
A.100° B.105° C.110° D.120°
5.已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2.图中全等的三角形共有( )
A.4对 B.3对 C.2对 D.1对
6.如图所示,∠B=∠C=90°,E是BC的中点,AE平分∠DAB,则下列说法正确的个数是( )
⑴DE平分∠CDA;⑵△EBA≌△EDA;⑶△EBA≌△DCE;⑷AB+CD=AD;⑸AE2+DE2=AD2
A.4个 B.3个 C.2个 D.1个
二、填空题
7.在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=2cm,过点E作EF⊥AC交CD的延长线于点F.若AE=3cm,则EF= cm.
8.如图,△ABC是等边三角形.在AC,BC边上各取一点P,Q,使 AP=CQ,且∠ABP=20°,AQ,BP相交于点O,则∠AQB= .
9.如图,线段AB、BC的垂直平分线l1、l2相交于点O,若∠1=37°,则∠AOC= .
10.如图,在锐角三角形ABC中,AB=4,△ABC的面积为10,BD平分∠ABC,若M、N分别是BD、BC上的动点,则CM+MN的最小值为
11.如图,在△ABC中,∠C=90°,BD为△ABC的角平分线,过点D作直线lAB,点P为直线l上的一个动点,若△BCD的面积为16,BC=8,则AP最小值为 .
12.如图,在△ABC中,BD、CE是△ABC的角平分线,BD,CE交于点O.过点O作OF⊥BC,垂足为F,若∠BAC=120°,OD OE=12,BC BE CD=5,则OF= .
三、综合题
13.如图,在 中,已知 的垂直平分线交 于点N,交 于点M,连接 .
(1)若 ,求 的度数.
(2)若 , 的周长是 .
①求 的长度;
②若点P为直线 上一点,请你求出 周长的最小值.
14.如图,在 中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G,交AB于点E,连接EG、EF.
(1)求证: .
(2)请你判断: 与EF的大小关系,并加以证明.
15.已知在中,P是的中点,B是延长线上的一点,连接,.
(1)如图1,若,,,,求的长;
(2)过点D作,交的延长线于点E,如图2所示,若,,求证:;
(3)如图3,若,是否存在实数m,使得当时,?若存在,请直接写出m的值;若不存在,请说明理由.
16.
(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段EF,BE,FD之间的数量关系.
小明同学探究的方法是:延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,
他的结论是 (直接写结论,不需证明);
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC,CD上的点,且∠EAF是∠BAD的二分之一,上述结论是否仍然成立,并说明理由.
(3)如图3,四边形ABCD是边长为5的正方形,∠EBF=45°,直接写出三角形DEF的周长.
17.八年级一班数学兴趣小组在一次活动中进行了探究试验活动,请你和他们一起活动吧.
(1)(探究与发现)
如图1,是的中线,延长至点,使,连接,写出图中全等的两个三角形
(2)(理解与应用)
填空:如图2,是的中线,若,,设,则的取值范围是 .
(3)已知:如图3,是的中线,,点在的延长线上,,求证:.
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】B
4.【答案】A
5.【答案】A
6.【答案】B
7.【答案】5
8.【答案】80°
9.【答案】76°
10.【答案】5
11.【答案】4
12.【答案】
13.【答案】(1)解:∵ ,
∴ ,
∴ ,
∵ 的垂直平分线交 于点N,
∴ ,
∴
(2)解:①∵ 是 的垂直平分线,
∴ ,
∴ 的周长 ,
∵ , 的周长是 ,
∴ ;
② 周长 最小,即 最小,
根据轴对称性质得,当点P与M重合时,即 最小,
此时 周长的值最小,
∴ 周长的最小值
14.【答案】(1)证明:∵BG∥AC,
∴ ,
∵D是BC的中点,
∴BD=DC,
在△BDG和△CDF中,
,
∴ ,
∴ ;
(2)解: ,
由 得 ,
∵ ,∴ ,
∵ ,∴ ,
∴ .
15.【答案】(1)解:∵,,
∴∠B=180°-∠CAB-∠ACB=180°-90°-60°=30°,
∴,
∵,
∴,
∴是等边三角形,
∴.
∵P是的中点,
∴.
在中,,
设,则,
∴,
∴,
∴(已舍去),
∴.
(2)证明:如图1,连接,
∵DE∥AC,
∴.
在和中,
,
∴△CPA≌△DPE(AAS),
∴,.
∵,
∴.
又∵DE∥AC,
∴,
∴是等边三角形,
∴,.
∵,
∴.
在△CAB和△EBA中,
,
∴△CAB≌△EBA(SAS),
∴,
∴.
(3)解:存在这样的m,m=.
16.【答案】(1)EF=BE+DF
(2)结论EF=BE+DF仍然成立;
理由:如图2,延长FD到点G.使DG=BE.连结AG
在△ABE和△ADG中,
∵,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
∵,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
(3)解:如图3,延长DC到点G,截取CG=AE,连接BG,
在△AEB与△CGB中,
∵
,
∴△AEB≌△CGB(SAS),
∴BE=BG,∠ABE=∠CBG.
∵∠EBF=45°,∠ABC=90°,
∴∠ABE+∠CBF=45°,
∴∠CBF+∠CBG=45°.
在△EBF与△GBF中,
∵,
∴△EBF≌△GBF(SAS),
∴EF=GF,
∴△DEF的周长=EF+ED+CF=AE+CF+DE+DF=AD+CD=10.
17.【答案】(1)
(2)
(3)证明:如图3,延长到,使,连接,
,
是的中线,
,
在与中,
,
,
,,
,
,,
,,
,
,
,
在与中,
,
,
.
1 / 1
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
