2.5 逆命题逆定理 课件(共17张PPT)
文档属性
| 名称 | 2.5 逆命题逆定理 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 152.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-17 19:55:29 | ||
图片预览



文档简介
(共17张PPT)
浙教版八上
2.5 逆命题和逆定理
领悟的,二线合一-----------等腰三角形
对某件事情作出判断的句子叫做命题。
命题的结构:命题由题设、结论组成
命题有真有假。
温故知新,齐声朗读:
正确的命题是真命题,错误的命题是假命题
真假
结论
条件
命题
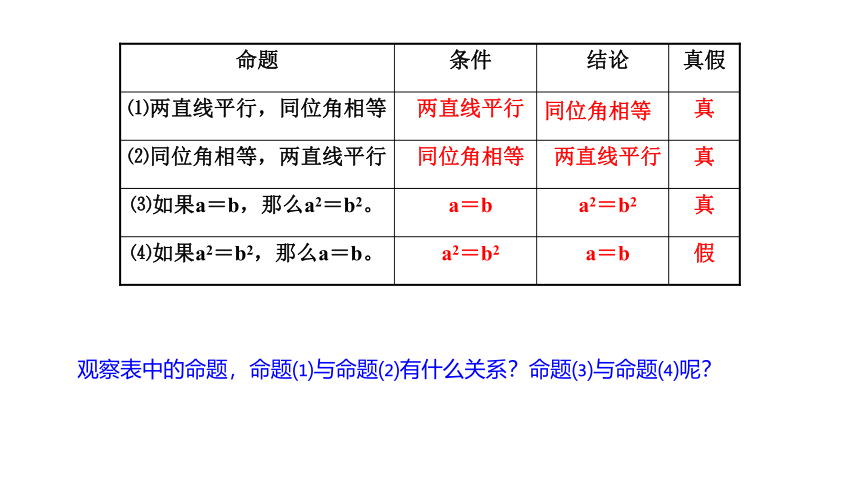
观察表中的命题,命题⑴与命题⑵有什么关系?命题⑶与命题⑷呢?
⑴两直线平行,同位角相等
两直线平行
同位角相等
真
⑵同位角相等,两直线平行
同位角相等
两直线平行
真
⑶如果a=b,那么a2=b2。
a=b
a2=b2
真
⑷如果a2=b2,那么a=b。
a2=b2
a=b
假
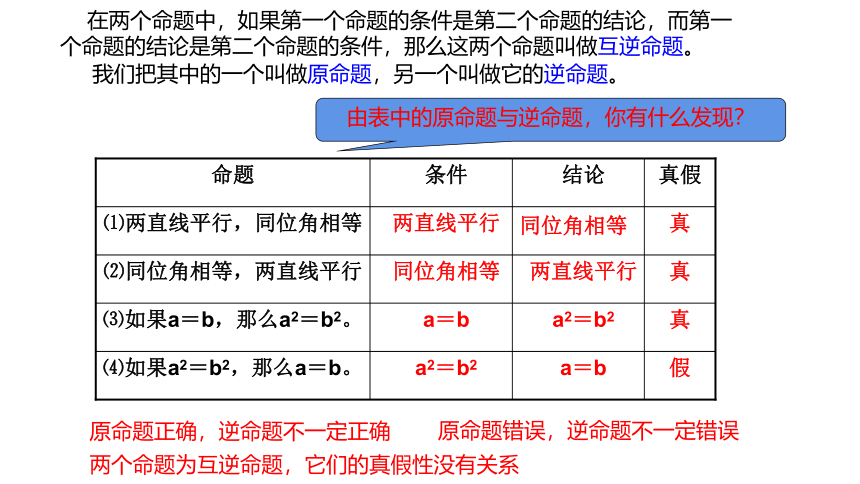
在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题。
我们把其中的一个叫做原命题,另一个叫做它的逆命题。
假
a=b
a2=b2
⑷如果a2=b2,那么a=b。
真
a2=b2
a=b
⑶如果a=b,那么a2=b2。
真
两直线平行
同位角相等
⑵同位角相等,两直线平行
真
同位角相等
两直线平行
⑴两直线平行,同位角相等
真假
结论
条件
命题
由表中的原命题与逆命题,你有什么发现?
原命题正确,逆命题不一定正确
原命题错误,逆命题不一定错误
两个命题为互逆命题,它们的真假性没有关系
定理:等腰三角形的两个底角相等。
如果一个定理的逆命题能被证明是真命题,那么就叫它是原定理的逆定理,这两个定理叫互逆定理。
有两个角相等的三角形是等腰三角形。
一个命题经证明是真命题,就可称为定理;
请说出其逆命题,并判断是真命题还是假命题:
这是一个真命题
请说出一对互逆定理
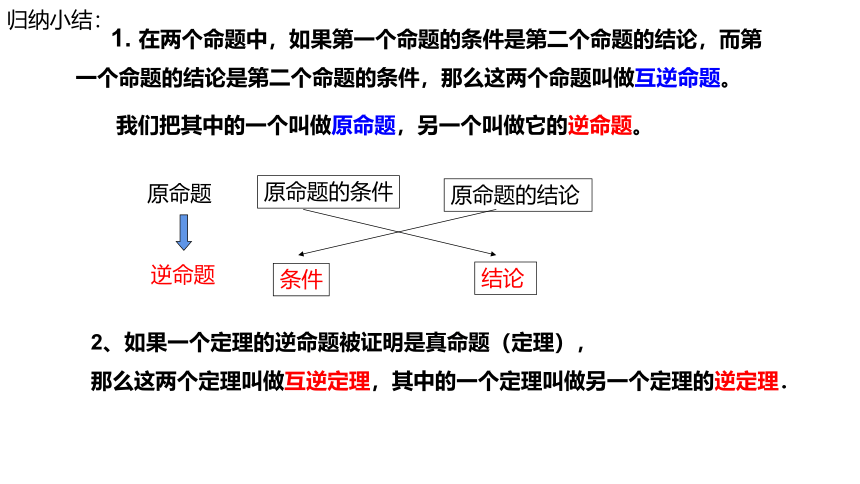
1. 在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题。
我们把其中的一个叫做原命题,另一个叫做它的逆命题。
原命题
逆命题
原命题的条件
结论
原命题的结论
条件
2、如果一个定理的逆命题被证明是真命题(定理),
那么这两个定理叫做互逆定理,其中的一个定理叫做另一个定理的逆定理.
归纳小结:
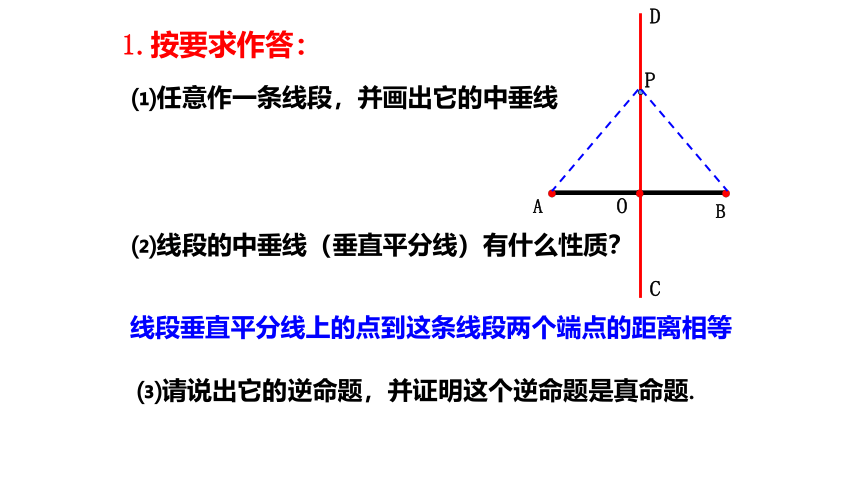
⑴任意作一条线段,并画出它的中垂线
⑵线段的中垂线(垂直平分线)有什么性质?
A
B
线段垂直平分线上的点到这条线段两个端点的距离相等
O
D
C
P
⑶请说出它的逆命题,并证明这个逆命题是真命题.
1.按要求作答:
A
P
B
已知:如图,AB是一条线段,P是一点,且PA=PB
求证:点P在线段AB的垂直平分线上
作PC⊥AB于点O
O
C
证明:
∵PA=PB,PO⊥AB,
∴OA=OB(等腰三角形三线合一性质)
∴PC是AB的垂直平分线。
∴点P在线段AB的垂直平分线上
解: 这个定理的逆命题是: 到线段两端距离相等的点,在这条线段的垂直平分线上.
⑵当点P在线段AB上,结论显然成立;
⑴当点P不在 线段AB上时,
A
B
P
P
P
P
P
P
显然,上述两个命题可称为互逆定理
线段垂直平分线性质定理:
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上
A
P
B
几何语言:
∵PA=PB
∴点P在AB的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
线段垂直平分线性质定理的逆定理:
线段垂直平分线性质定理的逆定理---------确定点P位置,点P在哪里?
2、说出命题“两个全等三角形的面积相等”的逆命题, 判断这个命题的真假,并给出证明。
解:逆命题:如果两个三角形的面积相等,那么这两个三角形全等
说明一个命题是真命题需经证明,而说明一个命题是假命题只需举一个反例。
假命题
15
4
┎
┍
4
┍
4
A
B
C1
C4
C2
C3
AB∥C1C2
同底等高的两个三角形面积相等
S△ABC1=S△ABC2=S△ABC3=S△ABC4
显然,
△ABC1≌△ABC2 ≌△ABC3 ≌△ABC4
1.下列说法哪些正确,哪些不正确?
(2)每个定理都有逆定理。
(1)每个命题都有逆命题。
(3)假命题没有逆命题。
(4)真命题的逆命题是真命题。
√
×
×
×
当堂检测:
2.说出下列各命题的逆命题,并判断互逆命题的真假:
(1)如果|a|=|b|,那么a=b;
逆命题:如果a=b,那么|a|=|b|
(3)磁悬浮列车是一种高速行驶时不接触地面的交通工具。
逆命题:高速行驶时不接触地面的交通工具是磁悬浮列车。
真命题
假命题
假命题
真命题
(4)角平分线上的点到角的两边距离相等。
真命题
逆命题:到角两边距离相等的点在这个角的角平分线上。真命题
(4) 同位角相等
假命题
相等的两个角是同位角
假命题
逆命题:
(5)等腰三角形两腰上的高线长相等
真命题
逆命题:
如果一个三角形有两条高线相等,那么这个三角形是等腰三角形
真命题
(6)
等角的补角相等
真命题
逆命题
如果两个角相等,那么这两个角是等角的补角
真命题
(7)
同角的余角相等
真命题
逆命题
如果两个角相等,那么这两个角是同角的余角
真命题
3.写出下列各命题的逆命题,并判断互逆命题的真假
连续递推,豁然开朗
逆命题:如果一个三角形的高线与中线互相重合,那么这个三角形是等腰三角形
已知:如图,在△ABC中,AD是高线也是中线.
求证:△ABC是等腰三角形
证明:
A
B
C
D
∵AD是高线
∴∠ADB=∠ADC=900
∵AD是中线.
∴BD=CD
在△ABD和△ACD中
∴△ABD ≌△ACD(SAS)
∴AB=AC
∴△ABC是等腰三角形
中线
+
高线
=
等腰三角形
3.写出定理“等腰三角形底边上的高线与中线互相重合”的逆命题,
并证明这个逆命题是真命题
.
4.写出定理“等腰三角形底边上的高线与顶角的平分线互相重合”的逆命题,
并证明这个逆命题是真命题
逆命题:如果一个三角形一边上的高线与该边所对角的平分线互相重合,
那么这个三角形是等腰三角形
已知:如图,在△ABC中,AD是高线也是角平分线.
求证:△ABC是等腰三角形
证明:
A
B
C
D
∵AD是高线
∴∠ADB=∠ADC
∵AD是角平分线.
∴∠BAD=∠CAD
在△ABD和△ACD中
∴△ABD ≌△ACD(SAS)
∴AB=AC
∴△ABC是等腰三角形
角平分线线
+
高线
=
等腰三角形
.
5.写出定理“等腰三角形底边上的中线与顶角的平分线互相重合”的逆命题,
并证明这个逆命题是真命题
逆命题:如果一个三角形一边上的中线与该边所对的角的平分线互相重合,
那么这个三角形是等腰三角形
已知:如图,在△ABC中,AD是中线也是角平分线.
求证:△ABC是等腰三角形
证明:
∵AD是中线
∴BD=CD
∵AD是角平分线.
∴∠BAD=∠CAD
∴△ABD ≌△ECD(SAS)
∴AB=EC
∴△ABC是等腰三角形
角平分线线
+
高线
=
等腰三角形
A
B
C
D
E
延长AD至E,使AD=DE ,连接CE
在△ABD和△ECD中
∴∠CED=∠CAD
AC=CE
∴AB=AC
∠BAD=∠CED
6.求证:三角形三条边的垂直平分线相较于一点
已知:如图,在△ABC中,DE,FH,MN分别为三边的垂直平分线.
求证:DE,FH,MN相交于一点.
A
B
C
M
N
F
H
D
E
P
证明:设DE与FH交于点P,连接AP,BP,PC
∵DE垂直平分BC
∴PB=PC
(线段垂直平分线上的点到线段两端的距离相等)
∵FH垂直平分AC
∴PC=PA
(线段垂直平分线上的点到线段两端的距离相等)
∴PB=PA
∴点P在AB的垂直平分线NN上
(到线段两端的距离相等的点在线段的垂直平分线上)
∴DE,FH,MN相交于一点
浙教版八上
2.5 逆命题和逆定理
领悟的,二线合一-----------等腰三角形
对某件事情作出判断的句子叫做命题。
命题的结构:命题由题设、结论组成
命题有真有假。
温故知新,齐声朗读:
正确的命题是真命题,错误的命题是假命题
真假
结论
条件
命题
观察表中的命题,命题⑴与命题⑵有什么关系?命题⑶与命题⑷呢?
⑴两直线平行,同位角相等
两直线平行
同位角相等
真
⑵同位角相等,两直线平行
同位角相等
两直线平行
真
⑶如果a=b,那么a2=b2。
a=b
a2=b2
真
⑷如果a2=b2,那么a=b。
a2=b2
a=b
假
在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题。
我们把其中的一个叫做原命题,另一个叫做它的逆命题。
假
a=b
a2=b2
⑷如果a2=b2,那么a=b。
真
a2=b2
a=b
⑶如果a=b,那么a2=b2。
真
两直线平行
同位角相等
⑵同位角相等,两直线平行
真
同位角相等
两直线平行
⑴两直线平行,同位角相等
真假
结论
条件
命题
由表中的原命题与逆命题,你有什么发现?
原命题正确,逆命题不一定正确
原命题错误,逆命题不一定错误
两个命题为互逆命题,它们的真假性没有关系
定理:等腰三角形的两个底角相等。
如果一个定理的逆命题能被证明是真命题,那么就叫它是原定理的逆定理,这两个定理叫互逆定理。
有两个角相等的三角形是等腰三角形。
一个命题经证明是真命题,就可称为定理;
请说出其逆命题,并判断是真命题还是假命题:
这是一个真命题
请说出一对互逆定理
1. 在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题。
我们把其中的一个叫做原命题,另一个叫做它的逆命题。
原命题
逆命题
原命题的条件
结论
原命题的结论
条件
2、如果一个定理的逆命题被证明是真命题(定理),
那么这两个定理叫做互逆定理,其中的一个定理叫做另一个定理的逆定理.
归纳小结:
⑴任意作一条线段,并画出它的中垂线
⑵线段的中垂线(垂直平分线)有什么性质?
A
B
线段垂直平分线上的点到这条线段两个端点的距离相等
O
D
C
P
⑶请说出它的逆命题,并证明这个逆命题是真命题.
1.按要求作答:
A
P
B
已知:如图,AB是一条线段,P是一点,且PA=PB
求证:点P在线段AB的垂直平分线上
作PC⊥AB于点O
O
C
证明:
∵PA=PB,PO⊥AB,
∴OA=OB(等腰三角形三线合一性质)
∴PC是AB的垂直平分线。
∴点P在线段AB的垂直平分线上
解: 这个定理的逆命题是: 到线段两端距离相等的点,在这条线段的垂直平分线上.
⑵当点P在线段AB上,结论显然成立;
⑴当点P不在 线段AB上时,
A
B
P
P
P
P
P
P
显然,上述两个命题可称为互逆定理
线段垂直平分线性质定理:
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上
A
P
B
几何语言:
∵PA=PB
∴点P在AB的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
线段垂直平分线性质定理的逆定理:
线段垂直平分线性质定理的逆定理---------确定点P位置,点P在哪里?
2、说出命题“两个全等三角形的面积相等”的逆命题, 判断这个命题的真假,并给出证明。
解:逆命题:如果两个三角形的面积相等,那么这两个三角形全等
说明一个命题是真命题需经证明,而说明一个命题是假命题只需举一个反例。
假命题
15
4
┎
┍
4
┍
4
A
B
C1
C4
C2
C3
AB∥C1C2
同底等高的两个三角形面积相等
S△ABC1=S△ABC2=S△ABC3=S△ABC4
显然,
△ABC1≌△ABC2 ≌△ABC3 ≌△ABC4
1.下列说法哪些正确,哪些不正确?
(2)每个定理都有逆定理。
(1)每个命题都有逆命题。
(3)假命题没有逆命题。
(4)真命题的逆命题是真命题。
√
×
×
×
当堂检测:
2.说出下列各命题的逆命题,并判断互逆命题的真假:
(1)如果|a|=|b|,那么a=b;
逆命题:如果a=b,那么|a|=|b|
(3)磁悬浮列车是一种高速行驶时不接触地面的交通工具。
逆命题:高速行驶时不接触地面的交通工具是磁悬浮列车。
真命题
假命题
假命题
真命题
(4)角平分线上的点到角的两边距离相等。
真命题
逆命题:到角两边距离相等的点在这个角的角平分线上。真命题
(4) 同位角相等
假命题
相等的两个角是同位角
假命题
逆命题:
(5)等腰三角形两腰上的高线长相等
真命题
逆命题:
如果一个三角形有两条高线相等,那么这个三角形是等腰三角形
真命题
(6)
等角的补角相等
真命题
逆命题
如果两个角相等,那么这两个角是等角的补角
真命题
(7)
同角的余角相等
真命题
逆命题
如果两个角相等,那么这两个角是同角的余角
真命题
3.写出下列各命题的逆命题,并判断互逆命题的真假
连续递推,豁然开朗
逆命题:如果一个三角形的高线与中线互相重合,那么这个三角形是等腰三角形
已知:如图,在△ABC中,AD是高线也是中线.
求证:△ABC是等腰三角形
证明:
A
B
C
D
∵AD是高线
∴∠ADB=∠ADC=900
∵AD是中线.
∴BD=CD
在△ABD和△ACD中
∴△ABD ≌△ACD(SAS)
∴AB=AC
∴△ABC是等腰三角形
中线
+
高线
=
等腰三角形
3.写出定理“等腰三角形底边上的高线与中线互相重合”的逆命题,
并证明这个逆命题是真命题
.
4.写出定理“等腰三角形底边上的高线与顶角的平分线互相重合”的逆命题,
并证明这个逆命题是真命题
逆命题:如果一个三角形一边上的高线与该边所对角的平分线互相重合,
那么这个三角形是等腰三角形
已知:如图,在△ABC中,AD是高线也是角平分线.
求证:△ABC是等腰三角形
证明:
A
B
C
D
∵AD是高线
∴∠ADB=∠ADC
∵AD是角平分线.
∴∠BAD=∠CAD
在△ABD和△ACD中
∴△ABD ≌△ACD(SAS)
∴AB=AC
∴△ABC是等腰三角形
角平分线线
+
高线
=
等腰三角形
.
5.写出定理“等腰三角形底边上的中线与顶角的平分线互相重合”的逆命题,
并证明这个逆命题是真命题
逆命题:如果一个三角形一边上的中线与该边所对的角的平分线互相重合,
那么这个三角形是等腰三角形
已知:如图,在△ABC中,AD是中线也是角平分线.
求证:△ABC是等腰三角形
证明:
∵AD是中线
∴BD=CD
∵AD是角平分线.
∴∠BAD=∠CAD
∴△ABD ≌△ECD(SAS)
∴AB=EC
∴△ABC是等腰三角形
角平分线线
+
高线
=
等腰三角形
A
B
C
D
E
延长AD至E,使AD=DE ,连接CE
在△ABD和△ECD中
∴∠CED=∠CAD
AC=CE
∴AB=AC
∠BAD=∠CED
6.求证:三角形三条边的垂直平分线相较于一点
已知:如图,在△ABC中,DE,FH,MN分别为三边的垂直平分线.
求证:DE,FH,MN相交于一点.
A
B
C
M
N
F
H
D
E
P
证明:设DE与FH交于点P,连接AP,BP,PC
∵DE垂直平分BC
∴PB=PC
(线段垂直平分线上的点到线段两端的距离相等)
∵FH垂直平分AC
∴PC=PA
(线段垂直平分线上的点到线段两端的距离相等)
∴PB=PA
∴点P在AB的垂直平分线NN上
(到线段两端的距离相等的点在线段的垂直平分线上)
∴DE,FH,MN相交于一点
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
