2.6直角三角形(2) 课件(共14张PPT)
文档属性
| 名称 | 2.6直角三角形(2) 课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 151.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-17 20:00:28 | ||
图片预览



文档简介
(共14张PPT)
浙教版八上
2.6 直角三角形(2)
领悟的,三连等+四连等
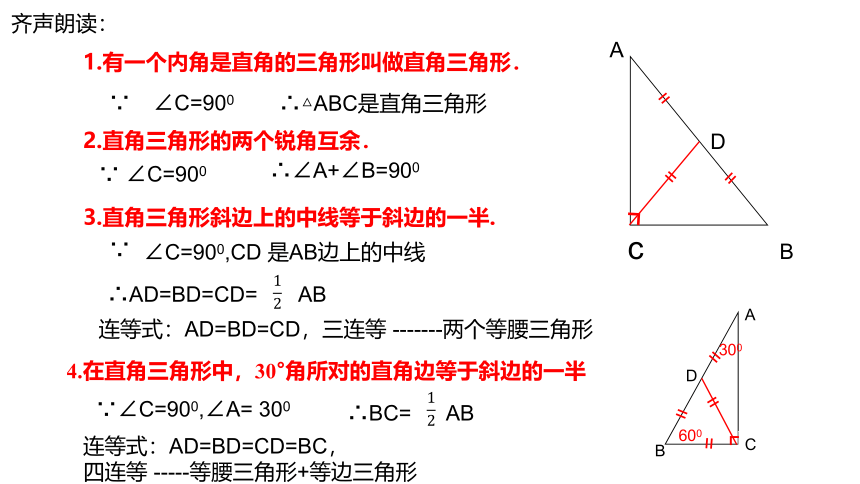
1.有一个内角是直角的三角形叫做直角三角形.
2.直角三角形的两个锐角互余.
3.直角三角形斜边上的中线等于斜边的一半.
4.在直角三角形中,30°角所对的直角边等于斜边的一半
齐声朗读:
A
B
c
┗
∴△ABC是直角三角形
∴∠A+∠B=900
∵∠C=900,∠A= 300
∵
∠C=900
∵
∠C=900
∵
∠C=900,CD 是AB边上的中线
D
=
=
=
∴AD=BD=CD= AB
A
B
C
┗
300
∴BC= AB
连等式:AD=BD=CD,三连等 -------两个等腰三角形
600
D
=
=
=
=
连等式:AD=BD=CD=BC,
四连等 -----等腰三角形+等边三角形
定理“直角三角形的两个锐角互余”
逆命题:两个锐角互余的三角形是直角三角形.
A
B
C
1.已知:如图,在△ABC中,∠A+∠B=90°.
求证:△ABC是直角三角形.
证明:∵∠A+∠B=90°(已知),
∠A+∠B+∠C=180°(三角形的内角为180°),
∴∠C=90°.
∴△ABC是直角三角形.
∴△ABC是直角三角形(有两个角互余的三角形是直角三角形)
C
A
D
B
三连等:AD=BD=CD
Rt△ABC
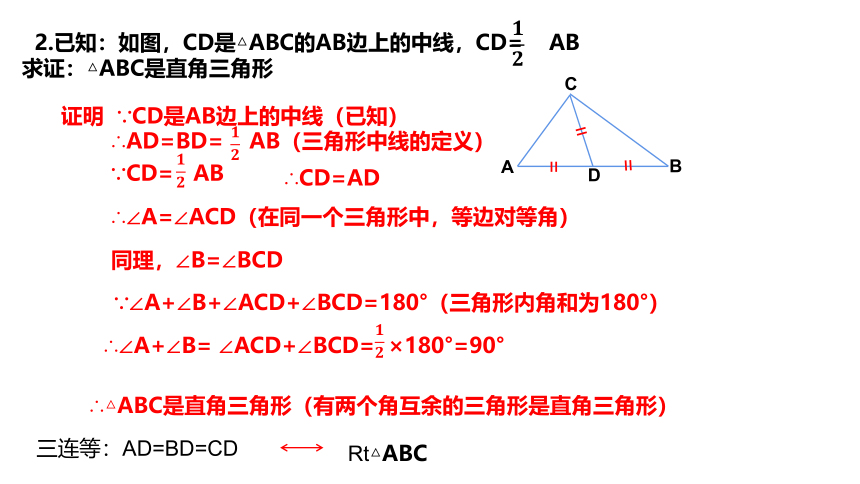
2.已知:如图,CD是△ABC的AB边上的中线,CD= AB
求证:△ABC是直角三角形
=
=
=
证明 ∵CD是AB边上的中线(已知)
∴AD=BD= AB(三角形中线的定义)
∵CD= AB
∴CD=AD
∴∠A=∠ACD(在同一个三角形中,等边对等角)
同理,∠B=∠BCD
∵∠A+∠B+∠ACD+∠BCD=180°(三角形内角和为180°)
∴∠A+∠B= ∠ACD+∠BCD= ×180°=90°
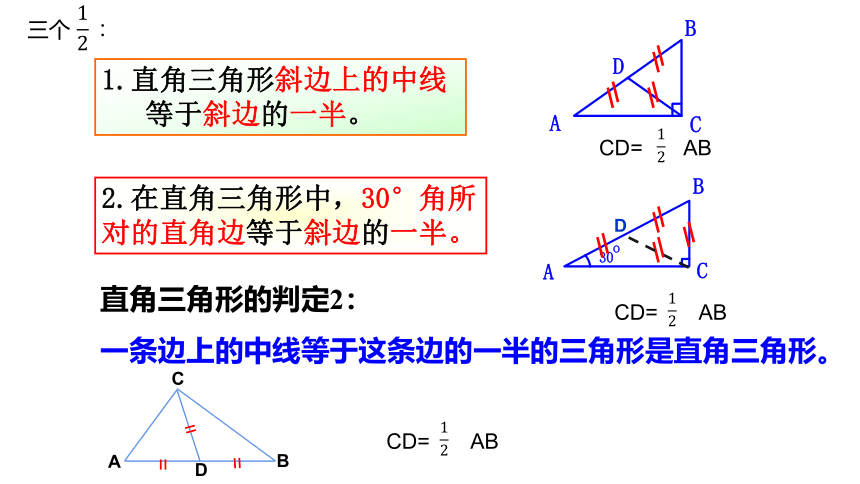
直角三角形的性质2:
直角三角形斜边上的中线等于斜边的一半
直角三角形的判定2:
一条边上的中线等于这条边的一半的三角形是直角三角形,这条边是这个直角三角形的斜边。
直角三角形的性质1:
直角三角形的两个锐角互余
直角三角形的判定1:
两个锐角互余的三角形是直角三角形
两对互逆定理:
1.直角三角形斜边上的中线
等于斜边的一半。
2.在直角三角形中,30°角所对的直角边等于斜边的一半。
直角三角形的判定2:
一条边上的中线等于这条边的一半的三角形是直角三角形。
D
CD= AB
CD= AB
三个
C
A
D
B
=
=
=
CD= AB
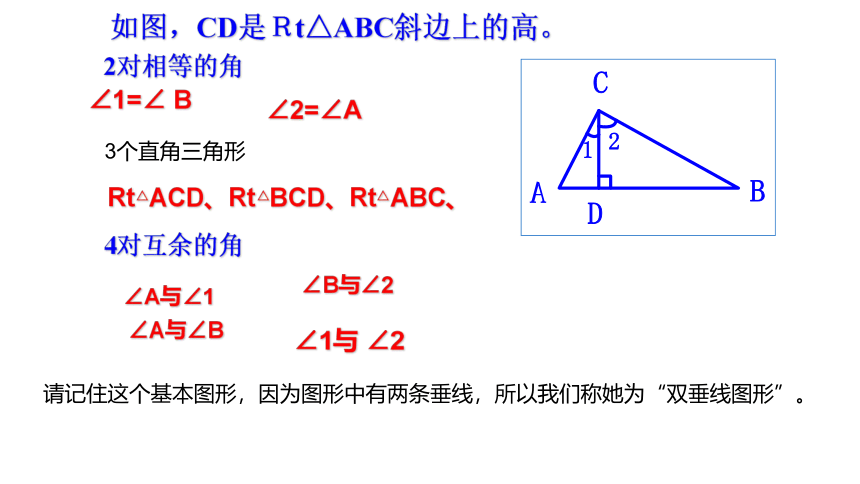
如图,CD是Rt△ABC斜边上的高。
Rt△ACD、Rt△BCD、Rt△ABC、
4对互余的角
2对相等的角
∠1=∠ B
∠A与∠B
∠A与∠1
∠B与∠2
∠1与 ∠2
∠2=∠A
3个直角三角形
请记住这个基本图形,因为图形中有两条垂线,所以我们称她为“双垂线图形”。
直角三角形的判定
1.有一个角是直角的三角形叫做直角三角形
2.有两个角互余的三角形是直角三角形
3、如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形.
课堂小结
1.如图:在Rt△ABC中∠A=300,AB+BC=12cm
则AB=_____cm
C
B
A
300
8
2.如图:△ABC是等边三角形,AD⊥BC,DE⊥AB,若AB=8cm, BD=___, BE=____
A
C
E
B
D
4cm
2cm
当堂检测:
┏
D
C
B
A
解:∵∠ABC=∠ACB=150
∴∠DAC=∠ABC+∠ACB=300
∴CD=1/2AC=a
3、 如图在△ABC中,AB=AC=2a,
∠ABC=∠ACB=150,CD是腰AB上的高,求CD的长
5、如图:已知 在△ABC 中,∠A=300, ∠ C=900,BD平分∠ABC.求证:AD=2DC
D
C
B
A
4、如图,在△ABC中,∠C=900,∠B=150, DE是AB的中垂线,BE=5,则AE=______,AC=_____
E
D
A
C
B
5
2.5
6.已知AB=AC,D是AB上一点,DE⊥BC于E,ED的延长线交CA的延长线于F,
求证: △ADF是等腰三角形.
倒推法:
△ADF是等腰三角形.
AF=DF
∠1=∠2
∠1=900-∠C
∠2=∠3=900-∠B
∠B=∠C
AB=AC
2
⌒
A
C
B
E
F
D
∟
1
⌒
⌒
3
连续递推,豁然开朗
7.如图,已知△ABC中,点A在DE上,CD⊥DE,
BE⊥DE,垂足分别是D,E.且AD=BE,CD=AE, △ABC是等腰直角三角形吗?说明理由.
倒推法:
┓
⌒
⌒
1
E
D
A
C
B
⌒
2
3
┓
△ABC是等腰直角三角形
AC=BC
∠BAC=900
△ACD ≌△BAE
.
∠1+∠2=900
∠2=∠3
9、如图,CD是斜边AB上的高,将Rt CBD沿CD折叠,B点恰好落在AB的中点E处,求∠A
8、已知:如图,∠BAC=90°,∠C=30°,
AD⊥BC于D,DE⊥AB于E,BE=1,求BC
B
A
C
D
E
A
B
C
D
E
标记符号,化繁为简;凸显关系,拨云见日
BE=1
BD=2
AB=4
BC=8
顺推法:
四连等
三连等
∠A=300
浙教版八上
2.6 直角三角形(2)
领悟的,三连等+四连等
1.有一个内角是直角的三角形叫做直角三角形.
2.直角三角形的两个锐角互余.
3.直角三角形斜边上的中线等于斜边的一半.
4.在直角三角形中,30°角所对的直角边等于斜边的一半
齐声朗读:
A
B
c
┗
∴△ABC是直角三角形
∴∠A+∠B=900
∵∠C=900,∠A= 300
∵
∠C=900
∵
∠C=900
∵
∠C=900,CD 是AB边上的中线
D
=
=
=
∴AD=BD=CD= AB
A
B
C
┗
300
∴BC= AB
连等式:AD=BD=CD,三连等 -------两个等腰三角形
600
D
=
=
=
=
连等式:AD=BD=CD=BC,
四连等 -----等腰三角形+等边三角形
定理“直角三角形的两个锐角互余”
逆命题:两个锐角互余的三角形是直角三角形.
A
B
C
1.已知:如图,在△ABC中,∠A+∠B=90°.
求证:△ABC是直角三角形.
证明:∵∠A+∠B=90°(已知),
∠A+∠B+∠C=180°(三角形的内角为180°),
∴∠C=90°.
∴△ABC是直角三角形.
∴△ABC是直角三角形(有两个角互余的三角形是直角三角形)
C
A
D
B
三连等:AD=BD=CD
Rt△ABC
2.已知:如图,CD是△ABC的AB边上的中线,CD= AB
求证:△ABC是直角三角形
=
=
=
证明 ∵CD是AB边上的中线(已知)
∴AD=BD= AB(三角形中线的定义)
∵CD= AB
∴CD=AD
∴∠A=∠ACD(在同一个三角形中,等边对等角)
同理,∠B=∠BCD
∵∠A+∠B+∠ACD+∠BCD=180°(三角形内角和为180°)
∴∠A+∠B= ∠ACD+∠BCD= ×180°=90°
直角三角形的性质2:
直角三角形斜边上的中线等于斜边的一半
直角三角形的判定2:
一条边上的中线等于这条边的一半的三角形是直角三角形,这条边是这个直角三角形的斜边。
直角三角形的性质1:
直角三角形的两个锐角互余
直角三角形的判定1:
两个锐角互余的三角形是直角三角形
两对互逆定理:
1.直角三角形斜边上的中线
等于斜边的一半。
2.在直角三角形中,30°角所对的直角边等于斜边的一半。
直角三角形的判定2:
一条边上的中线等于这条边的一半的三角形是直角三角形。
D
CD= AB
CD= AB
三个
C
A
D
B
=
=
=
CD= AB
如图,CD是Rt△ABC斜边上的高。
Rt△ACD、Rt△BCD、Rt△ABC、
4对互余的角
2对相等的角
∠1=∠ B
∠A与∠B
∠A与∠1
∠B与∠2
∠1与 ∠2
∠2=∠A
3个直角三角形
请记住这个基本图形,因为图形中有两条垂线,所以我们称她为“双垂线图形”。
直角三角形的判定
1.有一个角是直角的三角形叫做直角三角形
2.有两个角互余的三角形是直角三角形
3、如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形.
课堂小结
1.如图:在Rt△ABC中∠A=300,AB+BC=12cm
则AB=_____cm
C
B
A
300
8
2.如图:△ABC是等边三角形,AD⊥BC,DE⊥AB,若AB=8cm, BD=___, BE=____
A
C
E
B
D
4cm
2cm
当堂检测:
┏
D
C
B
A
解:∵∠ABC=∠ACB=150
∴∠DAC=∠ABC+∠ACB=300
∴CD=1/2AC=a
3、 如图在△ABC中,AB=AC=2a,
∠ABC=∠ACB=150,CD是腰AB上的高,求CD的长
5、如图:已知 在△ABC 中,∠A=300, ∠ C=900,BD平分∠ABC.求证:AD=2DC
D
C
B
A
4、如图,在△ABC中,∠C=900,∠B=150, DE是AB的中垂线,BE=5,则AE=______,AC=_____
E
D
A
C
B
5
2.5
6.已知AB=AC,D是AB上一点,DE⊥BC于E,ED的延长线交CA的延长线于F,
求证: △ADF是等腰三角形.
倒推法:
△ADF是等腰三角形.
AF=DF
∠1=∠2
∠1=900-∠C
∠2=∠3=900-∠B
∠B=∠C
AB=AC
2
⌒
A
C
B
E
F
D
∟
1
⌒
⌒
3
连续递推,豁然开朗
7.如图,已知△ABC中,点A在DE上,CD⊥DE,
BE⊥DE,垂足分别是D,E.且AD=BE,CD=AE, △ABC是等腰直角三角形吗?说明理由.
倒推法:
┓
⌒
⌒
1
E
D
A
C
B
⌒
2
3
┓
△ABC是等腰直角三角形
AC=BC
∠BAC=900
△ACD ≌△BAE
.
∠1+∠2=900
∠2=∠3
9、如图,CD是斜边AB上的高,将Rt CBD沿CD折叠,B点恰好落在AB的中点E处,求∠A
8、已知:如图,∠BAC=90°,∠C=30°,
AD⊥BC于D,DE⊥AB于E,BE=1,求BC
B
A
C
D
E
A
B
C
D
E
标记符号,化繁为简;凸显关系,拨云见日
BE=1
BD=2
AB=4
BC=8
顺推法:
四连等
三连等
∠A=300
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
