浙教版数学七年级上册6.1《几何图形》课时练习(含答案)
文档属性
| 名称 | 浙教版数学七年级上册6.1《几何图形》课时练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 169.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-18 21:52:24 | ||
图片预览


文档简介
2022-2023年浙教版数学七年级上册6.1
《几何图形》课时练习
一 、选择题
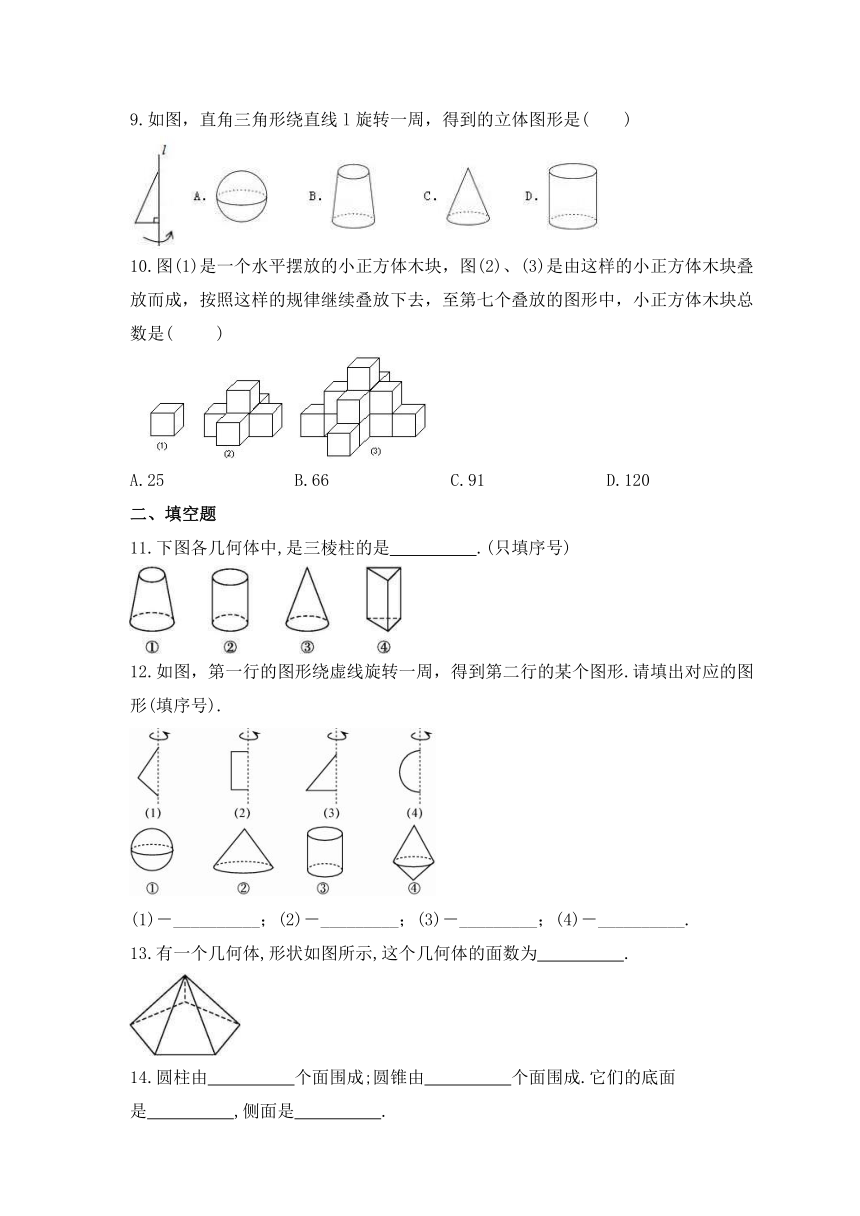
1.将下列如图的平面图形绕轴l旋转一周,可以得到的立体图形是( )
A. B. C. D.
2.按组成面的平或曲划分,与圆锥为同一类型几何体的是( )
A.正方体 B.长方体 C.球 D.棱柱
3.下列图形中,表示立体图形的有( )
A.1个 B.2个 C.3个 D.4个
4.下列物体的形状类似于球的是( )
A.茶杯 B.羽毛球 C.乒乓球 D.白炽灯泡
5.下列各组图形中都是平面图形的一组是( )
A.三角形、圆、球、圆锥
B.点、线、面、体
C.角、三角形、四边形、圆
D.点、相交线、线段、正方体
6.观察下图,把左边的图形绕着给定直线旋转一周后可能形成的几何体是( )
7.下列所列举的物体,与圆锥的形状类似的是( )
A.足球 B.字典 C.易拉罐 D.标枪的尖头
8.下面几种图形:①三角形;②长方形;③正方体;④圆;⑤圆锥;⑥圆柱.
其中属于立体图形的是( )
A.③⑤⑥ B.①②③ C.③⑥ D.④⑤
9.如图,直角三角形绕直线l旋转一周,得到的立体图形是( )
10.图(1)是一个水平摆放的小正方体木块,图(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数是( )
A.25 B.66 C.91 D.120
二 、填空题
11.下图各几何体中,是三棱柱的是 .(只填序号)
12.如图,第一行的图形绕虚线旋转一周,得到第二行的某个图形.请填出对应的图形(填序号).
(1)-__________;(2)-_________;(3)-_________;(4)-__________.
13.有一个几何体,形状如图所示,这个几何体的面数为 .
14.圆柱由 个面围成;圆锥由 个面围成.它们的底面是 ,侧面是 .
15.已知一个表面积为24dm2的正方体,则这个正方体的棱长为 .
16.如图,下列图形是将正三角形按一定规律排列,则第5个图形中所有正三角形的个数有 .
三 、解答题
17.如图是用七巧板拼出的图案,如果整个图案的面积是1,那么图中阴影部分的面积是多少?
18.如图.
(1)这个图象是平面图形还是立体图形?
(2)它有多少个面?多少条棱?多少个顶点?
(3)从它的表面看,你观察到哪些平面图形?
19.如图是一个几何体的平面展开图.
(1)这个几何体是 ;
(2)求这个几何体的体积.(π取3.14)
20.小明用若干个正方形和长方形准备拼成一个长方体的展开图,拼完后,小明看来看去觉得所拼图形似乎存在问题.
(1)请你帮小明分析一下拼图是否存在问题,若有多余图形,请将多余部分涂黑;若图形不全,则直接在原图中补全;
(2)若图中的正方形边长为5cm,长方形的长为8cm,请计算修正后所折叠而成的长方体的表面积.
21.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单的多面体模型,解答下列问题:
(1)根据上面的多面体模型,完成表格中的空格:
可以发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是____________;
(2)若一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是____________;
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处有3条棱.设该多面体外表面三角形的个数为x,八边形的个数为y,则x+y的值为____________.
参考答案
1.D
2.C
3.C
4.C.
5.C
6.D
7.D
8.A.
9.C.
10.C.
11.答案为:④
12.答案为:(1)④ (2)③ (3)② (4)①
13.答案为:6
14.答案为:3,2,平面,曲面
15.答案为:2dm.
16.答案为:485.
17.解:由题图可知,最大的等腰直角三角形的面积占七巧板拼出的图案面积的,
所以题图中阴影部分的面积为.
18.解:(1)立体图形
(2)4个面,6条棱,4个顶点.
(3)三角形
19.解:(1)圆柱;
(2)3.14×(10÷2)2×20=1 570(cm3).
20.解:(1)多余一个正方形,如图所示:
(2)表面积为52×2+8×5×4=50+160=210(cm)2.
21.解:(1)正八面体的顶点数为6,四面体的棱数为6.
V,F,E之间存在的关系为V+F-E=2.
(2)由题意可得F=V+8,即V=F-8.
由V+F-E=2可得F-8+F-30=2,解得F=20.
(3)∵V=24,且每个顶点处有3条棱,
∴E=24×3÷2=36.
由V+F-E=2,得F=2+36-24=14.
∴x+y=F=14.
《几何图形》课时练习
一 、选择题
1.将下列如图的平面图形绕轴l旋转一周,可以得到的立体图形是( )
A. B. C. D.
2.按组成面的平或曲划分,与圆锥为同一类型几何体的是( )
A.正方体 B.长方体 C.球 D.棱柱
3.下列图形中,表示立体图形的有( )
A.1个 B.2个 C.3个 D.4个
4.下列物体的形状类似于球的是( )
A.茶杯 B.羽毛球 C.乒乓球 D.白炽灯泡
5.下列各组图形中都是平面图形的一组是( )
A.三角形、圆、球、圆锥
B.点、线、面、体
C.角、三角形、四边形、圆
D.点、相交线、线段、正方体
6.观察下图,把左边的图形绕着给定直线旋转一周后可能形成的几何体是( )
7.下列所列举的物体,与圆锥的形状类似的是( )
A.足球 B.字典 C.易拉罐 D.标枪的尖头
8.下面几种图形:①三角形;②长方形;③正方体;④圆;⑤圆锥;⑥圆柱.
其中属于立体图形的是( )
A.③⑤⑥ B.①②③ C.③⑥ D.④⑤
9.如图,直角三角形绕直线l旋转一周,得到的立体图形是( )
10.图(1)是一个水平摆放的小正方体木块,图(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数是( )
A.25 B.66 C.91 D.120
二 、填空题
11.下图各几何体中,是三棱柱的是 .(只填序号)
12.如图,第一行的图形绕虚线旋转一周,得到第二行的某个图形.请填出对应的图形(填序号).
(1)-__________;(2)-_________;(3)-_________;(4)-__________.
13.有一个几何体,形状如图所示,这个几何体的面数为 .
14.圆柱由 个面围成;圆锥由 个面围成.它们的底面是 ,侧面是 .
15.已知一个表面积为24dm2的正方体,则这个正方体的棱长为 .
16.如图,下列图形是将正三角形按一定规律排列,则第5个图形中所有正三角形的个数有 .
三 、解答题
17.如图是用七巧板拼出的图案,如果整个图案的面积是1,那么图中阴影部分的面积是多少?
18.如图.
(1)这个图象是平面图形还是立体图形?
(2)它有多少个面?多少条棱?多少个顶点?
(3)从它的表面看,你观察到哪些平面图形?
19.如图是一个几何体的平面展开图.
(1)这个几何体是 ;
(2)求这个几何体的体积.(π取3.14)
20.小明用若干个正方形和长方形准备拼成一个长方体的展开图,拼完后,小明看来看去觉得所拼图形似乎存在问题.
(1)请你帮小明分析一下拼图是否存在问题,若有多余图形,请将多余部分涂黑;若图形不全,则直接在原图中补全;
(2)若图中的正方形边长为5cm,长方形的长为8cm,请计算修正后所折叠而成的长方体的表面积.
21.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单的多面体模型,解答下列问题:
(1)根据上面的多面体模型,完成表格中的空格:
可以发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是____________;
(2)若一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是____________;
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处有3条棱.设该多面体外表面三角形的个数为x,八边形的个数为y,则x+y的值为____________.
参考答案
1.D
2.C
3.C
4.C.
5.C
6.D
7.D
8.A.
9.C.
10.C.
11.答案为:④
12.答案为:(1)④ (2)③ (3)② (4)①
13.答案为:6
14.答案为:3,2,平面,曲面
15.答案为:2dm.
16.答案为:485.
17.解:由题图可知,最大的等腰直角三角形的面积占七巧板拼出的图案面积的,
所以题图中阴影部分的面积为.
18.解:(1)立体图形
(2)4个面,6条棱,4个顶点.
(3)三角形
19.解:(1)圆柱;
(2)3.14×(10÷2)2×20=1 570(cm3).
20.解:(1)多余一个正方形,如图所示:
(2)表面积为52×2+8×5×4=50+160=210(cm)2.
21.解:(1)正八面体的顶点数为6,四面体的棱数为6.
V,F,E之间存在的关系为V+F-E=2.
(2)由题意可得F=V+8,即V=F-8.
由V+F-E=2可得F-8+F-30=2,解得F=20.
(3)∵V=24,且每个顶点处有3条棱,
∴E=24×3÷2=36.
由V+F-E=2,得F=2+36-24=14.
∴x+y=F=14.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
