2.1 有理数的加法

课件29张PPT。有理数的加法
发放镇九年制学校：赵席年有理数的加法 教材分析 1.地位和作用：基础 2.教学目标：理解意义，掌握法则，准确运算；并培养学生观察，分析和概括的能力。 3.重点和难点：重点是有理数加法法则的理解和应用；异号两数相加是本节课的难点。 课前复习1.一个不等于0的有理数可看作由哪两个部分组成？（符号、绝对值）3.小学里学过什么数的加法运算？（正数及零的加法运算）2.比较下列各组数的绝对值哪个大？
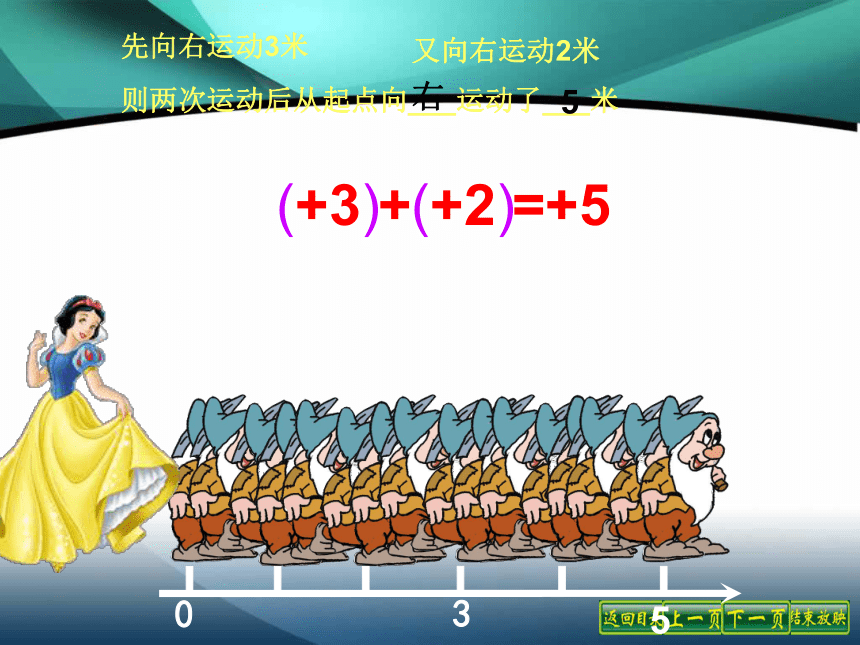
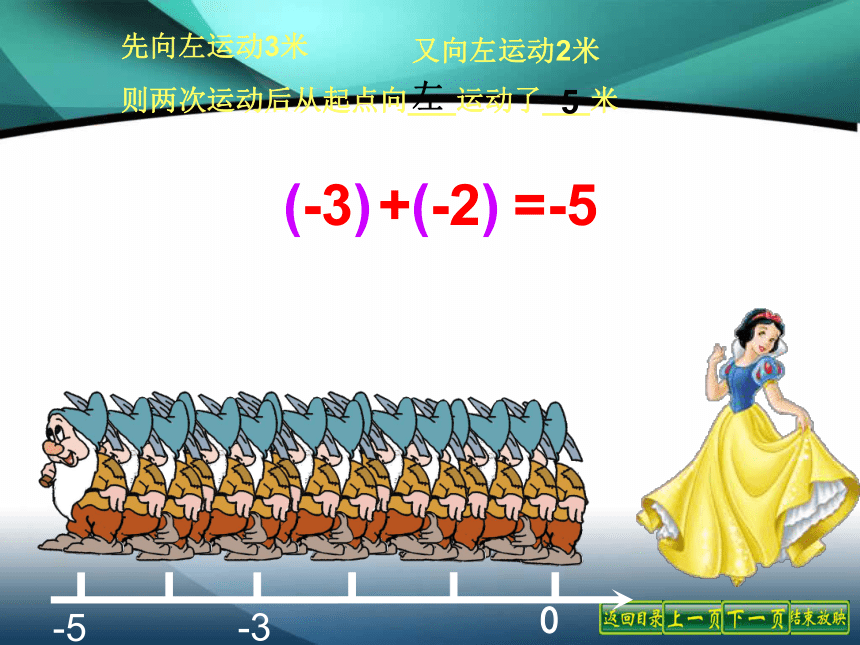
(1)－22与15； (2) 与 ; (3)2.7与－3.5.答案：(1)-22 (2) (3)-3.501234-1-2-3若规定向右为正,则向左为负向右运动3米记为: +3米向左运动1米记为:-1米?(+3)+(+2)=+5先向右运动3米又向右运动2米则两次运动后从起点向___运动了___米右5-3-5(-3)+(-2)=-5先向左运动3米又向左运动2米则两次运动后从起点向___运动了___米左5(+3)+(+2)=+5
( -3)+( -2)=-5同号两数相加,取相同的符号,
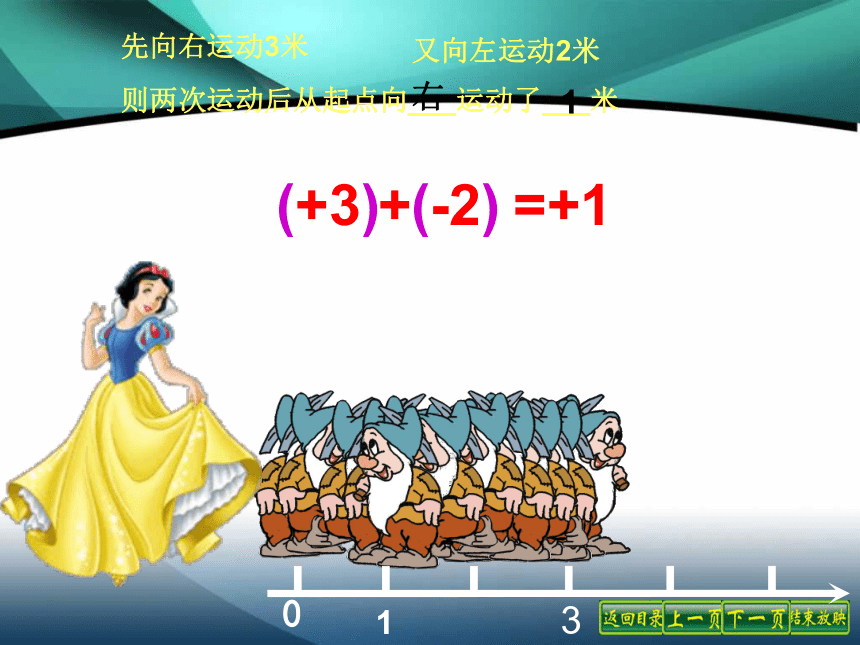
并把绝对值相加.找规律++--+-(2) (-3)+(-9)= -（3+9）= -12练一练(3) (-13)+(-8)= -（13+8）= -21(1) 6 + 11= +（6+11）= 17(1) 6 + 11(2)(-3)+(-9)(3)(-13)+(-8)解:31(+3)+(-2)=+1先向右运动3米又向左运动2米则两次运动后从起点向___运动了___米右1-3-1(-3)+(+2)=-1先向左运动3米又向右运动2米则两次运动后从起点向___运动了___米左1( 3) + ( 2) = 1
( 3) + ( 2) = 1绝对值不相等的异号两数相加,
取绝对值较大的数的符号,
并用较大的绝对值减去较小的绝对值.找规律--+++-(1) (-3)+ 9(4)(-4.7)+ 3.9= +（9-3）= 6=-(4.7-3.9)= -0.8练一练(2) 10 + (-6)(3) +(- )= +(10-6) = 4(1) (-3)+ 9(2) 10 + (-6)(3) +(- )解:(4)(-4.7)+ 3.93(+3)+(-3)=0先向右运动3米又向左运动3米则两次运动后____________回到起点(+3)+(-3)=0互为相反数的两个数相加得0找规律练一练(1) -79+79(2) 12+(-12)(3) 5+(-5)(4) (-3)+3= 0= 0= 0= 0-30+(-3)=-3先运动0米又向左运动3米则两次运动后从起点向___运动了___米左30+(-3)=-3一个数同0相加,仍得这个数找规律(1) 0+79(2) 0+(-12)(3) 5+0(4) (-3)+0练一练= 5= 79= -12= -3有理数的加法法则 1.同号两数相加,取相同的符号,并把
绝对值相加. 2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.相同符号取绝对值较大的加数的符号相加相减结果是0仍是这个数小结:分析特征 强化理解 总结步骤 ( - 4 ) + ( - 8 ) = - ( 4 + 8 )= - 12
↓ ↓ ↓
同号两数相加 取相同符号 通过绝对值化归
为算术数的加法
( - 9 ) + (+ 2) = - ( 9 - 2) = -7
↓ ↓ ↓
异号两数相加 取绝对值较大 通过绝对值化归
的加数的符号 为算术数的减法
同号两数之和——这是名符其实的和，做加法。
异号两数之和——表面上叫“和”，其实是做减法。 有理数中的“和”与小学算术中 “和”的比较结果 类型 结论：在有理数运算中，算术中的某些结论不一定再成立。 对比异同 强化记忆一 、接力口答：
1、 （+4）+（-7）
2、 （-8）+（-3）
3、 （-9）+（+5）
4、 （-6）+（+6）
5、 （-7）+0
6、 8+（-1）
7、 （-7）+1
8、 0+（-10）巩固练习二、计算：1、180+（-10）
2、（-10）+（-1）
3、45+（-45）
4、（-23）+0
5、（-25）+（-7）6、（-13）+5
7、（-1/2）+（+1/3）
8、2/3 +（-3/5）
9、（-0.9）+1.5
10、2.7+（-3.5）
=170=-11=0=-23=-32=-8=-1/6=1/15=0.6=-0.8记得要多练习呦!作业： 习题2.4 第1题请各位老师指导谢谢再见