浙教版数学九年级上册3.4圆心角课后练习 (含答案)
文档属性
| 名称 | 浙教版数学九年级上册3.4圆心角课后练习 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 190.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 00:00:00 | ||
图片预览


文档简介
浙教版初中数学九年级上册3.4圆心角-----课后练习
一、单选题
1.若圆的一条弦把圆分成度数比为1:5的两条弧,则优弧所对的圆心角为( )
A.60° B.300° C.30° D.150°
2.下列关于圆的说法,正确的是( )
A.弦是直径,直径也是弦
B.半圆是圆中最长的弧
C.圆的每一条直径所在的直线都是它的对称轴
D.过三点可以作一个圆
3.下列说法不正确的是 ( )
A.圆是轴对称图形,它有无数条对称轴;
B.圆的半径、弦长的一半、弦上的弦心距能组成一直角三角形,且圆的半径是此直角三角形的斜边;
C.弦长相等,则弦所对的弦心距也相等;
D.垂直于弦的直径平分这条弦,并且平分弦所对的弧。
4.下列命题中,正确的是()
A.平面上三个点确定一个圆
B.等弧所对的圆周角相等
C.平分弦的直径垂直于这条弦
D.与某圆一条半径垂直的直线是该圆的切线
5.如图,在三个等圆上各自有一条劣弧、、,如果+=,那么AB+CD与EF的大小关系是( )
A.AB+CD=EF B.AB+CD>EF
C.AB+CD<EF D.不能确定
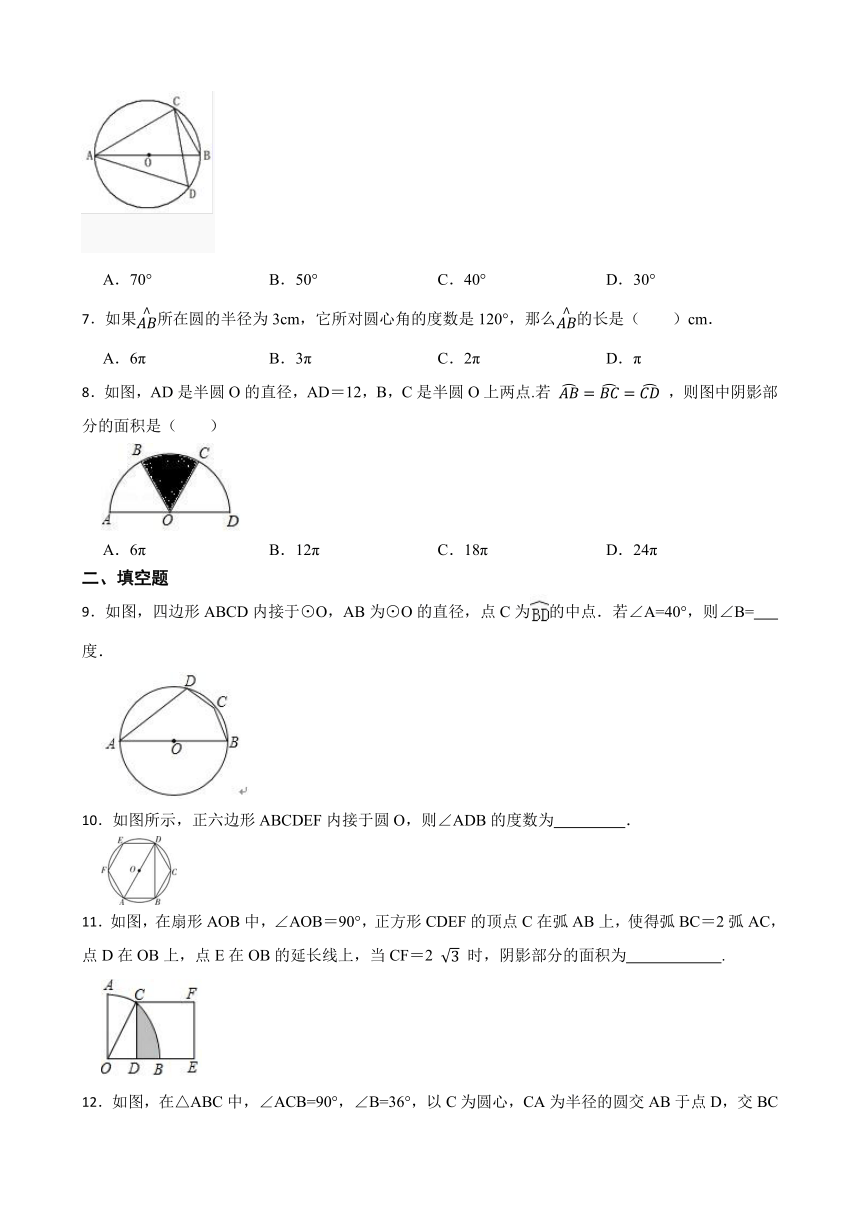
6.如图,AB为⊙O的直径,∠ DCB=30°, ∠ DAC=70°,则∠D的度数为
A.70° B.50° C.40° D.30°
7.如果所在圆的半径为3cm,它所对圆心角的度数是120°,那么的长是( )cm.
A.6π B.3π C.2π D.π
8.如图,AD是半圆O的直径,AD=12,B,C是半圆O上两点.若 ,则图中阴影部分的面积是( )
A.6π B.12π C.18π D.24π
二、填空题
9.如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为的中点.若∠A=40°,则∠B= 度.
10.如图所示,正六边形ABCDEF内接于圆O,则∠ADB的度数为 .
11.如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C在弧AB上,使得弧BC=2弧AC,点D在OB上,点E在OB的延长线上,当CF=2 时,阴影部分的面积为 .
12.如图,在△ABC中,∠ACB=90°,∠B=36°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E.求弧AD所对的圆心角的度数 .
13.如图,AB为⊙O直径,CD为⊙O的弦,∠ACD=25°,∠BAD的度数为 .
14.如图,四边形ABCD内接于⊙O,BC是⊙O的直径,AD∥BC,AC与BD相交于点P,若∠APB=50°,则∠PBC= .
15.将一个圆分割成3个扇形,使它们的圆心角的度数比为2:3:4,则这三个扇形的圆心角最小为 。
三、解答题
16.如图,AB、CD是⊙O的直径,弦CE∥AB,弧CE的度数为40°,求∠AOC的度数.
17.如图,点A、B、C、D、E都在⊙O上,AC平分∠BAD,且AB∥CE,求证:AD=CE.
18.如图,以 ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断弧 和弧 是否相等,并说明理由.
19.如图, 是 直径, 是 的弦, ,求 的度数.
20.如图,⊙ 中,弦 与 相交于点 , ,连接 .
求证:
(1) ;
(2) .
21.如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
22.如图,已知AB、CD为⊙O的两条弦, ,求证:AB=CD.
23.如图,已知AB为⊙O的直径,点C为半圆ACB上的动点(不与A、B两点重合),过点C作弦CD⊥AB,∠OCD的平分线交圆于点P,则点P的位置有何规律?请证明你的结论.
24.D、E是圆O的半径OA、OB上的点,CD⊥OA、CE⊥OB,CD=CE,则 弧CA与 弧CB 的关系是?
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】C
4.【答案】B
5.【答案】B
6.【答案】B
7.【答案】C
8.【答案】A
9.【答案】70
10.【答案】30°
11.【答案】
12.【答案】72°
13.【答案】65°
14.【答案】25°
15.【答案】80
16.【答案】解:连接OE,如图,
∵弧CE的度数为40°,
∴∠COE=40°,
∵OC=OE,
∴∠OCE=∠OEC,
∴∠OCE=(180°﹣40°)÷2=70°,
∵弦CE∥AB,
∴∠AOC=∠OCE=70°.
17.【答案】解:如图,∵AB∥CE,∴∠ACE=∠BAC.又∵AC平分∠BAD,∴∠BAC=∠DAC,∴∠C=∠CAD,∴ ,∴ ,∴ ,∴AD=CE.
18.【答案】解: ,
理由:连接AE.
∴AB=AE,
∴∠B=∠AEB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠B=∠GAF,∠FAE=∠AEB,
∴∠GAF=∠FAE,
∴ .
19.【答案】解:连接 .
是 的直径
.
=
即
20.【答案】证明:∵AB=CD,
∴ ,即 ,
∴
⑵ .
证明:∵ ,
∴AD=BC,
又∵∠ADE=∠CBE,∠DAE=∠BCE,
∴△ADE≌△CBE(ASA),
∴AE=CE
(1)证明:∵AB=CD,
∴ ,即 ,
∴
(2)证明:∵ ,
∴AD=BC,
又∵∠ADE=∠CBE,∠DAE=∠BCE,
∴△ADE≌△CBE(ASA),
∴AE=CE
21.【答案】(1)解:∵AB是半圆O的直径,
∴∠ACB=90°,
又∵OD∥BC,
∴∠AEO=90°,即OE⊥AC,
∠CAB=90°﹣∠B=90°﹣70°=20°,∠AOD=∠B=70°.
∵OA=OD,
∴∠DAO=∠ADO= = =55°
∴∠CAD=∠DAO﹣∠CAB=55°﹣20°=35°
(2)解:在直角△ABC中,BC= = = .
∵OE⊥AC,
∴AE=EC,
又∵OA=OB,
∴OE= BC= .
又∵OD= AB=2,
∴DE=OD﹣OE=2﹣ .
22.【答案】证明:∵ ,
∴ ,即 ,
∴AB=CD.
23.【答案】解:点P为半圆AB的中点.理由如下:
连接OP,如图,
∵∠OCD的平分线交圆于点P,
∴∠PCD=∠PCO,
∵OC=OP,
∴∠PCO=∠OPC,
∴∠PCD=∠OPC,
∴OP∥CD,
∵CD⊥AB,
∴OP⊥AB,
∴弧PA=弧PB,
即点P为半圆的中点.
24.【答案】解:
平分
∠1=∠2
∴
一、单选题
1.若圆的一条弦把圆分成度数比为1:5的两条弧,则优弧所对的圆心角为( )
A.60° B.300° C.30° D.150°
2.下列关于圆的说法,正确的是( )
A.弦是直径,直径也是弦
B.半圆是圆中最长的弧
C.圆的每一条直径所在的直线都是它的对称轴
D.过三点可以作一个圆
3.下列说法不正确的是 ( )
A.圆是轴对称图形,它有无数条对称轴;
B.圆的半径、弦长的一半、弦上的弦心距能组成一直角三角形,且圆的半径是此直角三角形的斜边;
C.弦长相等,则弦所对的弦心距也相等;
D.垂直于弦的直径平分这条弦,并且平分弦所对的弧。
4.下列命题中,正确的是()
A.平面上三个点确定一个圆
B.等弧所对的圆周角相等
C.平分弦的直径垂直于这条弦
D.与某圆一条半径垂直的直线是该圆的切线
5.如图,在三个等圆上各自有一条劣弧、、,如果+=,那么AB+CD与EF的大小关系是( )
A.AB+CD=EF B.AB+CD>EF
C.AB+CD<EF D.不能确定
6.如图,AB为⊙O的直径,∠ DCB=30°, ∠ DAC=70°,则∠D的度数为
A.70° B.50° C.40° D.30°
7.如果所在圆的半径为3cm,它所对圆心角的度数是120°,那么的长是( )cm.
A.6π B.3π C.2π D.π
8.如图,AD是半圆O的直径,AD=12,B,C是半圆O上两点.若 ,则图中阴影部分的面积是( )
A.6π B.12π C.18π D.24π
二、填空题
9.如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为的中点.若∠A=40°,则∠B= 度.
10.如图所示,正六边形ABCDEF内接于圆O,则∠ADB的度数为 .
11.如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C在弧AB上,使得弧BC=2弧AC,点D在OB上,点E在OB的延长线上,当CF=2 时,阴影部分的面积为 .
12.如图,在△ABC中,∠ACB=90°,∠B=36°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E.求弧AD所对的圆心角的度数 .
13.如图,AB为⊙O直径,CD为⊙O的弦,∠ACD=25°,∠BAD的度数为 .
14.如图,四边形ABCD内接于⊙O,BC是⊙O的直径,AD∥BC,AC与BD相交于点P,若∠APB=50°,则∠PBC= .
15.将一个圆分割成3个扇形,使它们的圆心角的度数比为2:3:4,则这三个扇形的圆心角最小为 。
三、解答题
16.如图,AB、CD是⊙O的直径,弦CE∥AB,弧CE的度数为40°,求∠AOC的度数.
17.如图,点A、B、C、D、E都在⊙O上,AC平分∠BAD,且AB∥CE,求证:AD=CE.
18.如图,以 ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断弧 和弧 是否相等,并说明理由.
19.如图, 是 直径, 是 的弦, ,求 的度数.
20.如图,⊙ 中,弦 与 相交于点 , ,连接 .
求证:
(1) ;
(2) .
21.如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
22.如图,已知AB、CD为⊙O的两条弦, ,求证:AB=CD.
23.如图,已知AB为⊙O的直径,点C为半圆ACB上的动点(不与A、B两点重合),过点C作弦CD⊥AB,∠OCD的平分线交圆于点P,则点P的位置有何规律?请证明你的结论.
24.D、E是圆O的半径OA、OB上的点,CD⊥OA、CE⊥OB,CD=CE,则 弧CA与 弧CB 的关系是?
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】C
4.【答案】B
5.【答案】B
6.【答案】B
7.【答案】C
8.【答案】A
9.【答案】70
10.【答案】30°
11.【答案】
12.【答案】72°
13.【答案】65°
14.【答案】25°
15.【答案】80
16.【答案】解:连接OE,如图,
∵弧CE的度数为40°,
∴∠COE=40°,
∵OC=OE,
∴∠OCE=∠OEC,
∴∠OCE=(180°﹣40°)÷2=70°,
∵弦CE∥AB,
∴∠AOC=∠OCE=70°.
17.【答案】解:如图,∵AB∥CE,∴∠ACE=∠BAC.又∵AC平分∠BAD,∴∠BAC=∠DAC,∴∠C=∠CAD,∴ ,∴ ,∴ ,∴AD=CE.
18.【答案】解: ,
理由:连接AE.
∴AB=AE,
∴∠B=∠AEB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠B=∠GAF,∠FAE=∠AEB,
∴∠GAF=∠FAE,
∴ .
19.【答案】解:连接 .
是 的直径
.
=
即
20.【答案】证明:∵AB=CD,
∴ ,即 ,
∴
⑵ .
证明:∵ ,
∴AD=BC,
又∵∠ADE=∠CBE,∠DAE=∠BCE,
∴△ADE≌△CBE(ASA),
∴AE=CE
(1)证明:∵AB=CD,
∴ ,即 ,
∴
(2)证明:∵ ,
∴AD=BC,
又∵∠ADE=∠CBE,∠DAE=∠BCE,
∴△ADE≌△CBE(ASA),
∴AE=CE
21.【答案】(1)解:∵AB是半圆O的直径,
∴∠ACB=90°,
又∵OD∥BC,
∴∠AEO=90°,即OE⊥AC,
∠CAB=90°﹣∠B=90°﹣70°=20°,∠AOD=∠B=70°.
∵OA=OD,
∴∠DAO=∠ADO= = =55°
∴∠CAD=∠DAO﹣∠CAB=55°﹣20°=35°
(2)解:在直角△ABC中,BC= = = .
∵OE⊥AC,
∴AE=EC,
又∵OA=OB,
∴OE= BC= .
又∵OD= AB=2,
∴DE=OD﹣OE=2﹣ .
22.【答案】证明:∵ ,
∴ ,即 ,
∴AB=CD.
23.【答案】解:点P为半圆AB的中点.理由如下:
连接OP,如图,
∵∠OCD的平分线交圆于点P,
∴∠PCD=∠PCO,
∵OC=OP,
∴∠PCO=∠OPC,
∴∠PCD=∠OPC,
∴OP∥CD,
∵CD⊥AB,
∴OP⊥AB,
∴弧PA=弧PB,
即点P为半圆的中点.
24.【答案】解:
平分
∠1=∠2
∴
同课章节目录
