浙教版数学九年级上册3.3垂径定理同步练习 (含答案)
文档属性
| 名称 | 浙教版数学九年级上册3.3垂径定理同步练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 333.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 16:44:30 | ||
图片预览



文档简介
2022-2023学年浙教版数学九年级上册3.3 垂径定理 同步练习
一、单选题
1.如图,⊙O的半径为5,弦AB=6,P是弦AB上的一个动点(不与A、B重合),下列符合条件的OP的值可以是( )
A.3.1 B.4.2 C.5.3 D.6.4
2.如图,AB是的弦,OC⊥AB于点C,连结OB,P是半径OB上任意一点,连结AP,若OB=5,OC=3,则AP的长不可能是( ).
A.6 B.7 C.8 D.9
3.如图,在⊙O中,半径OC⊥AB于点D.已知OC=5,OD=4,则弦AB的长为( )
A.3 B.4 C.5 D.6
4.如图,在⊙O中,CD是⊙O的直径,AB⊥CD于点E,若AB=8,CE=2,则⊙O的半径为( )
A. B. C.3 D.5
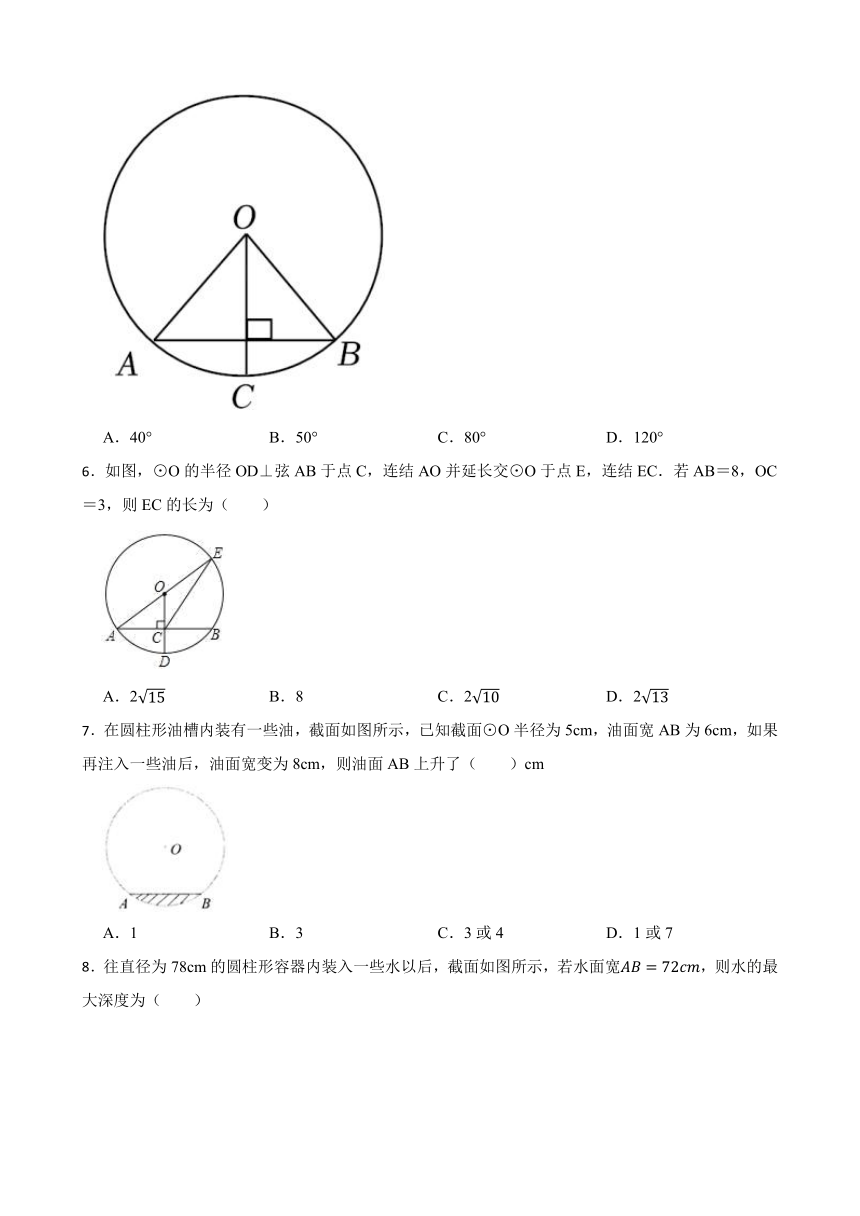
5.如图,在⊙O中,OC⊥AB,若∠BOC=40°,则∠OAB等于( )
A.40° B.50° C.80° D.120°
6.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,OC=3,则EC的长为( )
A.2 B.8 C.2 D.2
7.在圆柱形油槽内装有一些油,截面如图所示,已知截面⊙O半径为5cm,油面宽AB为6cm,如果再注入一些油后,油面宽变为8cm,则油面AB上升了( )cm
A.1 B.3 C.3或4 D.1或7
8.往直径为78cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽,则水的最大深度为( )
A.36 cm B.27 cm C.24 cm D.15 cm
9.半径等于4的圆中,垂直平分半径的弦长为( )
A. B. C. D.
10.如图,AB是⊙O的直径,弦CD⊥AB于点E,连接AD,若AB=10,CD=8,则AD的长为( )
A.8 B.2 C.3 D.4
二、填空题
11.如图,舞台地面上有一段以点O为圆心的,某同学要站在的中点C的位置上.于是他想:只要从点O出发,沿着与弦垂直的方向走到上,就能找到的中点C,老师肯定了他的想法.这位同学确定点C所用方法的依据是 .
12.如图,在平面直角坐标系中,每个小正方形的边长均为1个单位长度,点O、A、B、C均在格点上,则过A、B、C三点的圆的圆心坐标为 .
13.如图,CD是⊙O的直径,AB是弦,CD⊥AB,若OB=5,AB=8,则AC的长为 .
14.数学活动课上,小东想测算一个圆形齿轮内圈圆的半径.如图所示,小东首先在内圈圆上取点A,B,再作弦AB的垂直平分线,垂足为C,交于点D,连接CD,经测量cm,cm,那么这个齿轮内圈圆的半径为 cm.
15.如图,点 在半圆 上,BC是直径, .若 ,则BC的长为 .
16.如图,AB为⊙O的直径,弦CD⊥AB于点H,若AB=10,CD=8,则OH的长为
三、解答题
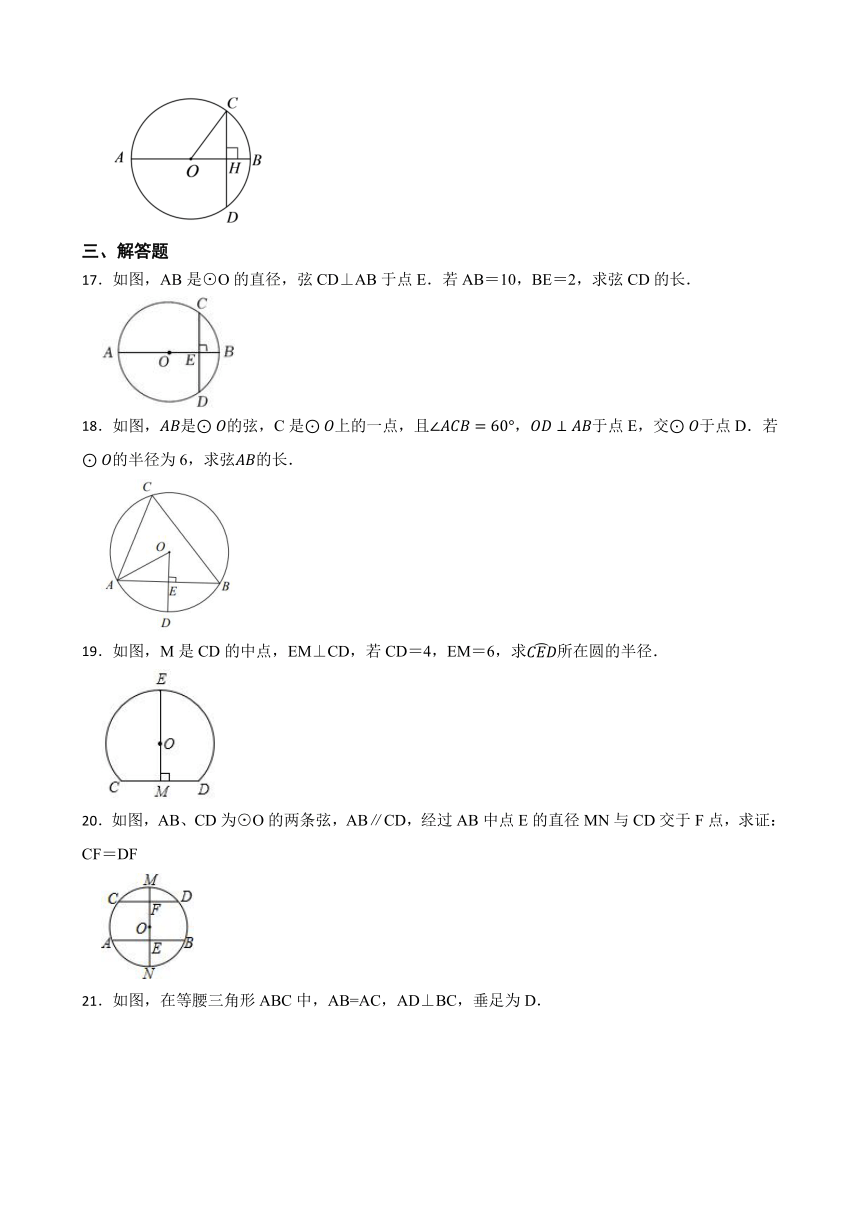
17.如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=10,BE=2,求弦CD的长.
18.如图,是的弦,C是上的一点,且,于点E,交于点D.若的半径为6,求弦的长.
19.如图,M是CD的中点,EM⊥CD,若CD=4,EM=6,求所在圆的半径.
20.如图,AB、CD为⊙O的两条弦,AB∥CD,经过AB中点E的直径MN与CD交于F点,求证:CF=DF
21.如图,在等腰三角形ABC中,AB=AC,AD⊥BC,垂足为D.
(1)请用尺规作图作出三角形ABC的外接圆⊙O;(不写作法及证明,应保留作图痕迹)
(2)若BC=4,AD=5,求⊙O的半径r.
22.如图,AB是 的直径,弦 于点M,连结CO,CB.
(1)若 , ,求CD的长度;
(2)若 平分 ,求证: .
23.如图,以点O为圆心的两个同心圆中,大圆的弦AB切小圆于点P.
(1)PA与PB的数量关系是 ;
(2)若AB=12,求圆环的面积.
24.如图,有一座圆弧形拱桥,它的跨度AB为30m,拱高PM为9m,当洪水泛滥到跨度只有15m时,就要采取紧急措施,若某次洪水中,拱顶离水面只有2m,即PN=2m时,试求:
(1)拱桥所在的圆的半径;
(2)通过计算说明是否需要采取紧急措施.
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】D
4.【答案】D
5.【答案】B
6.【答案】D
7.【答案】D
8.【答案】C
9.【答案】A
10.【答案】D
11.【答案】垂径定理
12.【答案】(1,4)
13.【答案】
14.【答案】5
15.【答案】
16.【答案】3
17.【答案】解:连接,如图所示:
为的直径,,
,,
,
在中,由勾股定理得:,
.
18.【答案】解:如图,连接OB,
则∠AOB=2∠ACB=120°,
∵OD⊥AB,
∴∠AOE=∠AOB=60°,
∵AO=6,
∴在Rt△AOE中,,
∴AB=2AE,
故答案为:.
19.【答案】解:连接OC,
∵M是CD的中点,EM⊥CD,
∴EM过⊙O的圆心点O, CM=CD=2 ,
设半径为x,
∵EM=6,
∴OM=EM-OE=6-x,
在Rt△OCM中,OM2+CM2=OC2, 即(6-x)2+22=x2,
解得:x=.
∴所在圆的半径为.
20.【答案】证明:∵E为AB中点,MN过圆心O,
∴MN⊥AB ,
∴∠MEB=90°,
∵AB∥CD ,
∴∠MFD=∠MEB=90°,
即MN⊥CD ,
∴CF=DF.
21.【答案】(1)解:∵AB=AC,AD⊥BC,
∴BD=CD,即AD垂直平分BC,
∴作AB边的垂直平分线交AD于点O,再以O点为圆心,OA长为半径画圆,⊙O即为所求作,如下图所示;
(2)解:连结OB,
∵AB=AC,AD⊥BC,BC=4,
∴BD=CD=2 ,
设⊙O的半径为r,则AO=BO=r,,
在Rt△BOD中,由勾股定理可得:
,
解得:,
∴⊙O的半径.
22.【答案】(1)解:∵AB是⊙O的直径,弦CD⊥AB,
∴CM=DM,
∵AM=2,BM=8,
∴AB=10,
∴OA=OC=5,
在Rt△OCM中,OM2+CM2=OC2,
∴CM 4,
∴CD=8;
(2)证明:过点O作ON⊥BC,垂足为N,
∵CO平分∠DCB,
∴OM=ON,
∵CO=CO
∴Rt△COM≌Rt△CON
∴CM=CN
∴CB=CD.
23.【答案】(1)PA=PB
(2)解:如图,连接
24.【答案】(1)解:设圆弧所在圆的圆心为O,连接OA、OA′,
设半径为xm,
则OA=OA′=OP,
由垂径定理可知AM=BM,A′N=B′N,
∵AB=30m,
∴AM= AB=15(m),
在Rt△AOM中,OM=OP﹣PM=(x﹣9)m,
由勾股定理可得:AO2=OM2+AM2,
即x2=(x﹣9)2+152,
解得:x=17,
即拱桥所在的圆的半径为17m;
(2)解:∵OP=17m,
∴ON=OP﹣PN=17﹣2=15(m),
在Rt△A′ON中,由勾股定理可得A′N= =8(m),
∴A′B′=2A'N=16米>15m,
∴不需要采取紧急措施.
一、单选题
1.如图,⊙O的半径为5,弦AB=6,P是弦AB上的一个动点(不与A、B重合),下列符合条件的OP的值可以是( )
A.3.1 B.4.2 C.5.3 D.6.4
2.如图,AB是的弦,OC⊥AB于点C,连结OB,P是半径OB上任意一点,连结AP,若OB=5,OC=3,则AP的长不可能是( ).
A.6 B.7 C.8 D.9
3.如图,在⊙O中,半径OC⊥AB于点D.已知OC=5,OD=4,则弦AB的长为( )
A.3 B.4 C.5 D.6
4.如图,在⊙O中,CD是⊙O的直径,AB⊥CD于点E,若AB=8,CE=2,则⊙O的半径为( )
A. B. C.3 D.5
5.如图,在⊙O中,OC⊥AB,若∠BOC=40°,则∠OAB等于( )
A.40° B.50° C.80° D.120°
6.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,OC=3,则EC的长为( )
A.2 B.8 C.2 D.2
7.在圆柱形油槽内装有一些油,截面如图所示,已知截面⊙O半径为5cm,油面宽AB为6cm,如果再注入一些油后,油面宽变为8cm,则油面AB上升了( )cm
A.1 B.3 C.3或4 D.1或7
8.往直径为78cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽,则水的最大深度为( )
A.36 cm B.27 cm C.24 cm D.15 cm
9.半径等于4的圆中,垂直平分半径的弦长为( )
A. B. C. D.
10.如图,AB是⊙O的直径,弦CD⊥AB于点E,连接AD,若AB=10,CD=8,则AD的长为( )
A.8 B.2 C.3 D.4
二、填空题
11.如图,舞台地面上有一段以点O为圆心的,某同学要站在的中点C的位置上.于是他想:只要从点O出发,沿着与弦垂直的方向走到上,就能找到的中点C,老师肯定了他的想法.这位同学确定点C所用方法的依据是 .
12.如图,在平面直角坐标系中,每个小正方形的边长均为1个单位长度,点O、A、B、C均在格点上,则过A、B、C三点的圆的圆心坐标为 .
13.如图,CD是⊙O的直径,AB是弦,CD⊥AB,若OB=5,AB=8,则AC的长为 .
14.数学活动课上,小东想测算一个圆形齿轮内圈圆的半径.如图所示,小东首先在内圈圆上取点A,B,再作弦AB的垂直平分线,垂足为C,交于点D,连接CD,经测量cm,cm,那么这个齿轮内圈圆的半径为 cm.
15.如图,点 在半圆 上,BC是直径, .若 ,则BC的长为 .
16.如图,AB为⊙O的直径,弦CD⊥AB于点H,若AB=10,CD=8,则OH的长为
三、解答题
17.如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=10,BE=2,求弦CD的长.
18.如图,是的弦,C是上的一点,且,于点E,交于点D.若的半径为6,求弦的长.
19.如图,M是CD的中点,EM⊥CD,若CD=4,EM=6,求所在圆的半径.
20.如图,AB、CD为⊙O的两条弦,AB∥CD,经过AB中点E的直径MN与CD交于F点,求证:CF=DF
21.如图,在等腰三角形ABC中,AB=AC,AD⊥BC,垂足为D.
(1)请用尺规作图作出三角形ABC的外接圆⊙O;(不写作法及证明,应保留作图痕迹)
(2)若BC=4,AD=5,求⊙O的半径r.
22.如图,AB是 的直径,弦 于点M,连结CO,CB.
(1)若 , ,求CD的长度;
(2)若 平分 ,求证: .
23.如图,以点O为圆心的两个同心圆中,大圆的弦AB切小圆于点P.
(1)PA与PB的数量关系是 ;
(2)若AB=12,求圆环的面积.
24.如图,有一座圆弧形拱桥,它的跨度AB为30m,拱高PM为9m,当洪水泛滥到跨度只有15m时,就要采取紧急措施,若某次洪水中,拱顶离水面只有2m,即PN=2m时,试求:
(1)拱桥所在的圆的半径;
(2)通过计算说明是否需要采取紧急措施.
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】D
4.【答案】D
5.【答案】B
6.【答案】D
7.【答案】D
8.【答案】C
9.【答案】A
10.【答案】D
11.【答案】垂径定理
12.【答案】(1,4)
13.【答案】
14.【答案】5
15.【答案】
16.【答案】3
17.【答案】解:连接,如图所示:
为的直径,,
,,
,
在中,由勾股定理得:,
.
18.【答案】解:如图,连接OB,
则∠AOB=2∠ACB=120°,
∵OD⊥AB,
∴∠AOE=∠AOB=60°,
∵AO=6,
∴在Rt△AOE中,,
∴AB=2AE,
故答案为:.
19.【答案】解:连接OC,
∵M是CD的中点,EM⊥CD,
∴EM过⊙O的圆心点O, CM=CD=2 ,
设半径为x,
∵EM=6,
∴OM=EM-OE=6-x,
在Rt△OCM中,OM2+CM2=OC2, 即(6-x)2+22=x2,
解得:x=.
∴所在圆的半径为.
20.【答案】证明:∵E为AB中点,MN过圆心O,
∴MN⊥AB ,
∴∠MEB=90°,
∵AB∥CD ,
∴∠MFD=∠MEB=90°,
即MN⊥CD ,
∴CF=DF.
21.【答案】(1)解:∵AB=AC,AD⊥BC,
∴BD=CD,即AD垂直平分BC,
∴作AB边的垂直平分线交AD于点O,再以O点为圆心,OA长为半径画圆,⊙O即为所求作,如下图所示;
(2)解:连结OB,
∵AB=AC,AD⊥BC,BC=4,
∴BD=CD=2 ,
设⊙O的半径为r,则AO=BO=r,,
在Rt△BOD中,由勾股定理可得:
,
解得:,
∴⊙O的半径.
22.【答案】(1)解:∵AB是⊙O的直径,弦CD⊥AB,
∴CM=DM,
∵AM=2,BM=8,
∴AB=10,
∴OA=OC=5,
在Rt△OCM中,OM2+CM2=OC2,
∴CM 4,
∴CD=8;
(2)证明:过点O作ON⊥BC,垂足为N,
∵CO平分∠DCB,
∴OM=ON,
∵CO=CO
∴Rt△COM≌Rt△CON
∴CM=CN
∴CB=CD.
23.【答案】(1)PA=PB
(2)解:如图,连接
24.【答案】(1)解:设圆弧所在圆的圆心为O,连接OA、OA′,
设半径为xm,
则OA=OA′=OP,
由垂径定理可知AM=BM,A′N=B′N,
∵AB=30m,
∴AM= AB=15(m),
在Rt△AOM中,OM=OP﹣PM=(x﹣9)m,
由勾股定理可得:AO2=OM2+AM2,
即x2=(x﹣9)2+152,
解得:x=17,
即拱桥所在的圆的半径为17m;
(2)解:∵OP=17m,
∴ON=OP﹣PN=17﹣2=15(m),
在Rt△A′ON中,由勾股定理可得A′N= =8(m),
∴A′B′=2A'N=16米>15m,
∴不需要采取紧急措施.
同课章节目录
