浙教版数学九年级上册3.5圆周角课后练习 (含答案)
文档属性
| 名称 | 浙教版数学九年级上册3.5圆周角课后练习 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 213.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 16:45:15 | ||
图片预览




文档简介
浙教版初中数学九年级上册3.5圆周角---课后练习
一、单选题
1.如图,△ABC内接于⊙O,若∠A=45°,OC=2,则BC的长为( )
A. B. C. D.2
2.如图,∠AOB是⊙O的圆心角,∠AOB=80°,则弧AB所对圆周角∠ACB的度数是( )
A.40° B.45° C.50° D.80°
3.下列说法正确的是( )
A.平分弦的直径垂直于弦
B.相等的圆周角所对的弧相等
C.三个点确定一个圆
D.半圆或直径所对的圆周角是直角
4.如图,△ABC内接于⊙O,OD⊥BC于D,∠A=50°,则∠OCD的度数是( )
A.40° B.45° C.50° D.60°
5.如图,AB是⊙0的直径,点C、D在⊙0上,∠BOD=11O°,AD∥OC,则∠AOC=( )
A.70° B.60° C.50° D.55°
6.如图,CD是⊙O的直径,弦AB⊥CD于E,∠BCD=25°,则下列结论错误的是( )
A.AE=BE B.OE=DE
C.∠AOD=50° D.D是 的中点
7.已知:如图,∠BPC=50°,∠ABC=60°,则∠ACB是( )
A.40° B.50° C.60° D.70°
8.如图,在Rt△ACB中,∠ACB= ,AC=6,BC=8,若以AC为直径的☉O交AB于点D,则CD的长为( )
A. B. C. D.5
9.如图,AB是⊙O的直径,AB⊥CD于点E,连接CO,AD.若∠BAD=20°,则( )
A.AD=2OB B.CE=EO
C.∠OCE=40° D.∠BOC=2∠BAD
10.如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:①△AED≌△DFB:②GC平分∠BGD;③S四边形BCDG= CG2;④∠BGE的大小为定值.其中正确的结论个数为( )
A.1 B.2 C.3 D.4
二、填空题
11.如图,五边形ABCD内接于⊙O,若AC=AD,∠B+∠E=230°,则∠ACD的度数是 .
12.如图,点O为所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D= .
13.如图,以△ABC的边BC为直径的圆O分别交AB,AC于点D,E,连接OD、OE.若
∠A=70°,则∠DOE= °.
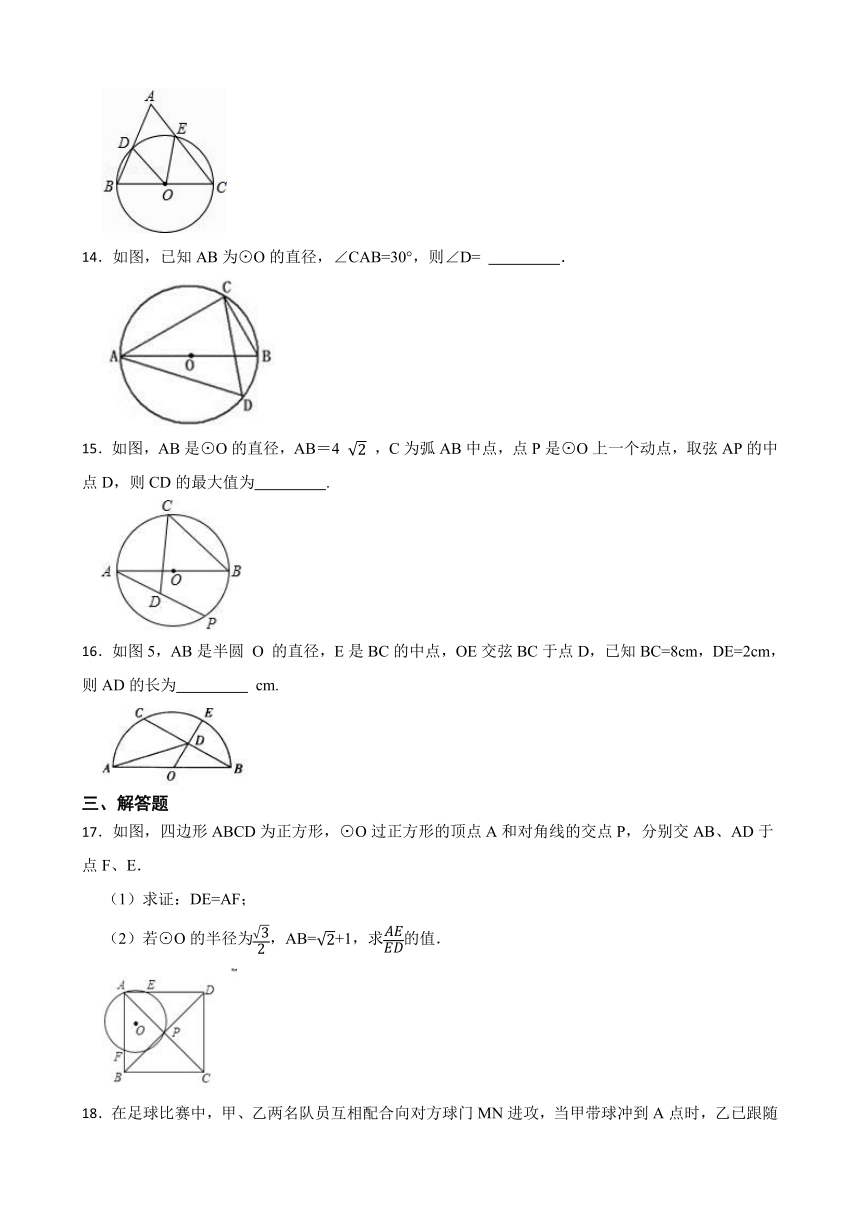
14.如图,已知AB为⊙O的直径,∠CAB=30°,则∠D= .
15.如图,AB是⊙O的直径,AB=4 ,C为弧AB中点,点P是⊙O上一个动点,取弦AP的中点D,则CD的最大值为 .
16.如图5,AB是半圆 O 的直径,E是BC的中点,OE交弦BC于点D,已知BC=8cm,DE=2cm,则AD的长为 cm.
三、解答题
17.如图,四边形ABCD为正方形,⊙O过正方形的顶点A和对角线的交点P,分别交AB、AD于点F、E.
(1)求证:DE=AF;
(2)若⊙O的半径为,AB=+1,求的值.
18.在足球比赛中,甲、乙两名队员互相配合向对方球门MN进攻,当甲带球冲到A点时,乙已跟随冲到B点,如图24-1-4-12.此时,甲自己直接射门好,还是迅速将球传给乙,让乙射门好?
19.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=8,CD=2,求EC的长.
20.如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°.
(1)求∠B的大小;
(2)已知圆心0到BD的距离为3,求AD的长.
21.如图, 为等边三角形,将 边绕点 顺时针旋转 ,得到线段 连接 ,求 的度数﹒
22.如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE.
(1)求证:四边形AECD为平行四边形;
(2)连接CO,求证:CO平分∠BCE.
23.如图,等腰三角形ABC中,BA=BC,以AB为直径作圆,交BC于点E,圆心为O.在EB上截取ED=EC,连接AD并延长,交⊙O于点F,连接OE、EF.
(1)试判断△ACD的形状,并说明理由;
(2)求证:∠ADE=∠OEF.
答案解析部分
1.【答案】A
2.【答案】A
3.【答案】D
4.【答案】A
5.【答案】D
6.【答案】B
7.【答案】D
8.【答案】C
9.【答案】D
10.【答案】D
11.【答案】65°
12.【答案】28°
13.【答案】40°
14.【答案】60°
15.【答案】 +
16.【答案】2
17.【答案】(1)证明:连接EP、FP,如图,
∵四边形ABCD为正方形,
∴∠BAD=90°,∠BPA=90°
∴∠FPE=90°,
∴∠BPF=∠APE,
又∵∠FBP=∠PAE=45°,
∴△BPF≌△APE,
∴BF=AE,
而AB=AD,
∴DE=AF;
(2)解:连EF,
∵∠BAD=90°,
∴EF为⊙O的直径,
而⊙O的半径为,
∴EF=,
∴AF2+AE2=EF2=()2=3①,
而DE=AF,
DE2+AE2=3;
又∵AD=AE+ED=AB,
∴AE+ED=+1②,
由①②联立起来组成方程组,解之得:AE=1,ED=或AE=,ED=1,
所以:=或=
提示:(1)连接EF、EP、FP,可证明△AEP≌△BFP
(2)设:AE=x,ED=AF=y
可得:x+y=和x2+y2=3,
解得x=,y=1或x=1,y=,
所以:=或=.
18.【答案】考虑过M、N及A、B中任一点作圆,这里不妨过M、N、B作圆,则A点在圆外,设MA交⊙O于C,则∠MAN<∠MCN,而∠MCN=∠MBN,所以∠MAN<∠MBN.因此在B点射门为好.
19.【答案】解:连结BE,如图,∵OD⊥AB,∴AC=BC= AB= ×8=4,设AO=x,则OC=OD﹣CD=x﹣2,在Rt△ACO中,∵ ,∴ ,解得 x=5,∴AE=10,OC=3,∵AE是直径,∴∠ABE=90°,∵OC是△ABE的中位线,∴BE=2OC=6,在Rt△CBE中,CE= .
20.【答案】解:(1)∵∠CAB=∠CDB(同弧所对的圆周角相等),∠CAB=40°,∴∠CDB=40°;又∵∠APD=65°,∴∠BPD=115°;∴在△BPD中,∴∠B=180°﹣∠CDB﹣∠BPD=25°;(2)过点O作OE⊥BD于点E,则OE=3.∵AB是直径,∴AD⊥BD(直径所对的圆周角是直角);∴OE∥AD;又∵O是AB的中点,∴OE是△ABD的中位线,∴AD=2OE=6.
21.【答案】解: 为等边三角形,
,
将 边绕点 顾时针旋转 ,
,
, ,
,
.
22.【答案】(1)证明:由圆周角定理得,∠B=∠E,又∠B=∠D,
∴∠E=∠D,
∵CE∥AD,
∴∠D+∠ECD=180°,
∴∠E+∠ECD=180°,
∴AE∥CD,
∴四边形AECD为平行四边形。
(2)证明:作OM⊥BC于M,ON⊥CE于N,
∵四边形AECD为平行四边形,
∴AD=CE,又AD=BC,
∴CE=CB,
∴OM=ON,又OM⊥BC,ON⊥CE,
∴CO平分∠BCE。
23.【答案】解:(1)△ACD是等腰三角形.理由:连接AE,∵AB是⊙O的直径,∴∠AED=90°,∴AE⊥CD,∵CE=ED,∴AC=AD,∴△ACD是等腰三角形;(2)证明:∵∠ADE=∠DEF+∠F,∠OEF=∠OED+∠DEF,而∠OED=∠B,∠B=∠F,∴∠ADE=∠OEF.
一、单选题
1.如图,△ABC内接于⊙O,若∠A=45°,OC=2,则BC的长为( )
A. B. C. D.2
2.如图,∠AOB是⊙O的圆心角,∠AOB=80°,则弧AB所对圆周角∠ACB的度数是( )
A.40° B.45° C.50° D.80°
3.下列说法正确的是( )
A.平分弦的直径垂直于弦
B.相等的圆周角所对的弧相等
C.三个点确定一个圆
D.半圆或直径所对的圆周角是直角
4.如图,△ABC内接于⊙O,OD⊥BC于D,∠A=50°,则∠OCD的度数是( )
A.40° B.45° C.50° D.60°
5.如图,AB是⊙0的直径,点C、D在⊙0上,∠BOD=11O°,AD∥OC,则∠AOC=( )
A.70° B.60° C.50° D.55°
6.如图,CD是⊙O的直径,弦AB⊥CD于E,∠BCD=25°,则下列结论错误的是( )
A.AE=BE B.OE=DE
C.∠AOD=50° D.D是 的中点
7.已知:如图,∠BPC=50°,∠ABC=60°,则∠ACB是( )
A.40° B.50° C.60° D.70°
8.如图,在Rt△ACB中,∠ACB= ,AC=6,BC=8,若以AC为直径的☉O交AB于点D,则CD的长为( )
A. B. C. D.5
9.如图,AB是⊙O的直径,AB⊥CD于点E,连接CO,AD.若∠BAD=20°,则( )
A.AD=2OB B.CE=EO
C.∠OCE=40° D.∠BOC=2∠BAD
10.如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:①△AED≌△DFB:②GC平分∠BGD;③S四边形BCDG= CG2;④∠BGE的大小为定值.其中正确的结论个数为( )
A.1 B.2 C.3 D.4
二、填空题
11.如图,五边形ABCD内接于⊙O,若AC=AD,∠B+∠E=230°,则∠ACD的度数是 .
12.如图,点O为所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D= .
13.如图,以△ABC的边BC为直径的圆O分别交AB,AC于点D,E,连接OD、OE.若
∠A=70°,则∠DOE= °.
14.如图,已知AB为⊙O的直径,∠CAB=30°,则∠D= .
15.如图,AB是⊙O的直径,AB=4 ,C为弧AB中点,点P是⊙O上一个动点,取弦AP的中点D,则CD的最大值为 .
16.如图5,AB是半圆 O 的直径,E是BC的中点,OE交弦BC于点D,已知BC=8cm,DE=2cm,则AD的长为 cm.
三、解答题
17.如图,四边形ABCD为正方形,⊙O过正方形的顶点A和对角线的交点P,分别交AB、AD于点F、E.
(1)求证:DE=AF;
(2)若⊙O的半径为,AB=+1,求的值.
18.在足球比赛中,甲、乙两名队员互相配合向对方球门MN进攻,当甲带球冲到A点时,乙已跟随冲到B点,如图24-1-4-12.此时,甲自己直接射门好,还是迅速将球传给乙,让乙射门好?
19.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=8,CD=2,求EC的长.
20.如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°.
(1)求∠B的大小;
(2)已知圆心0到BD的距离为3,求AD的长.
21.如图, 为等边三角形,将 边绕点 顺时针旋转 ,得到线段 连接 ,求 的度数﹒
22.如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE.
(1)求证:四边形AECD为平行四边形;
(2)连接CO,求证:CO平分∠BCE.
23.如图,等腰三角形ABC中,BA=BC,以AB为直径作圆,交BC于点E,圆心为O.在EB上截取ED=EC,连接AD并延长,交⊙O于点F,连接OE、EF.
(1)试判断△ACD的形状,并说明理由;
(2)求证:∠ADE=∠OEF.
答案解析部分
1.【答案】A
2.【答案】A
3.【答案】D
4.【答案】A
5.【答案】D
6.【答案】B
7.【答案】D
8.【答案】C
9.【答案】D
10.【答案】D
11.【答案】65°
12.【答案】28°
13.【答案】40°
14.【答案】60°
15.【答案】 +
16.【答案】2
17.【答案】(1)证明:连接EP、FP,如图,
∵四边形ABCD为正方形,
∴∠BAD=90°,∠BPA=90°
∴∠FPE=90°,
∴∠BPF=∠APE,
又∵∠FBP=∠PAE=45°,
∴△BPF≌△APE,
∴BF=AE,
而AB=AD,
∴DE=AF;
(2)解:连EF,
∵∠BAD=90°,
∴EF为⊙O的直径,
而⊙O的半径为,
∴EF=,
∴AF2+AE2=EF2=()2=3①,
而DE=AF,
DE2+AE2=3;
又∵AD=AE+ED=AB,
∴AE+ED=+1②,
由①②联立起来组成方程组,解之得:AE=1,ED=或AE=,ED=1,
所以:=或=
提示:(1)连接EF、EP、FP,可证明△AEP≌△BFP
(2)设:AE=x,ED=AF=y
可得:x+y=和x2+y2=3,
解得x=,y=1或x=1,y=,
所以:=或=.
18.【答案】考虑过M、N及A、B中任一点作圆,这里不妨过M、N、B作圆,则A点在圆外,设MA交⊙O于C,则∠MAN<∠MCN,而∠MCN=∠MBN,所以∠MAN<∠MBN.因此在B点射门为好.
19.【答案】解:连结BE,如图,∵OD⊥AB,∴AC=BC= AB= ×8=4,设AO=x,则OC=OD﹣CD=x﹣2,在Rt△ACO中,∵ ,∴ ,解得 x=5,∴AE=10,OC=3,∵AE是直径,∴∠ABE=90°,∵OC是△ABE的中位线,∴BE=2OC=6,在Rt△CBE中,CE= .
20.【答案】解:(1)∵∠CAB=∠CDB(同弧所对的圆周角相等),∠CAB=40°,∴∠CDB=40°;又∵∠APD=65°,∴∠BPD=115°;∴在△BPD中,∴∠B=180°﹣∠CDB﹣∠BPD=25°;(2)过点O作OE⊥BD于点E,则OE=3.∵AB是直径,∴AD⊥BD(直径所对的圆周角是直角);∴OE∥AD;又∵O是AB的中点,∴OE是△ABD的中位线,∴AD=2OE=6.
21.【答案】解: 为等边三角形,
,
将 边绕点 顾时针旋转 ,
,
, ,
,
.
22.【答案】(1)证明:由圆周角定理得,∠B=∠E,又∠B=∠D,
∴∠E=∠D,
∵CE∥AD,
∴∠D+∠ECD=180°,
∴∠E+∠ECD=180°,
∴AE∥CD,
∴四边形AECD为平行四边形。
(2)证明:作OM⊥BC于M,ON⊥CE于N,
∵四边形AECD为平行四边形,
∴AD=CE,又AD=BC,
∴CE=CB,
∴OM=ON,又OM⊥BC,ON⊥CE,
∴CO平分∠BCE。
23.【答案】解:(1)△ACD是等腰三角形.理由:连接AE,∵AB是⊙O的直径,∴∠AED=90°,∴AE⊥CD,∵CE=ED,∴AC=AD,∴△ACD是等腰三角形;(2)证明:∵∠ADE=∠DEF+∠F,∠OEF=∠OED+∠DEF,而∠OED=∠B,∠B=∠F,∴∠ADE=∠OEF.
同课章节目录
