浙教版数学九年级上册 3.8弧长及扇形的面积 课后练习(含答案)
文档属性
| 名称 | 浙教版数学九年级上册 3.8弧长及扇形的面积 课后练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 230.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 00:00:00 | ||
图片预览


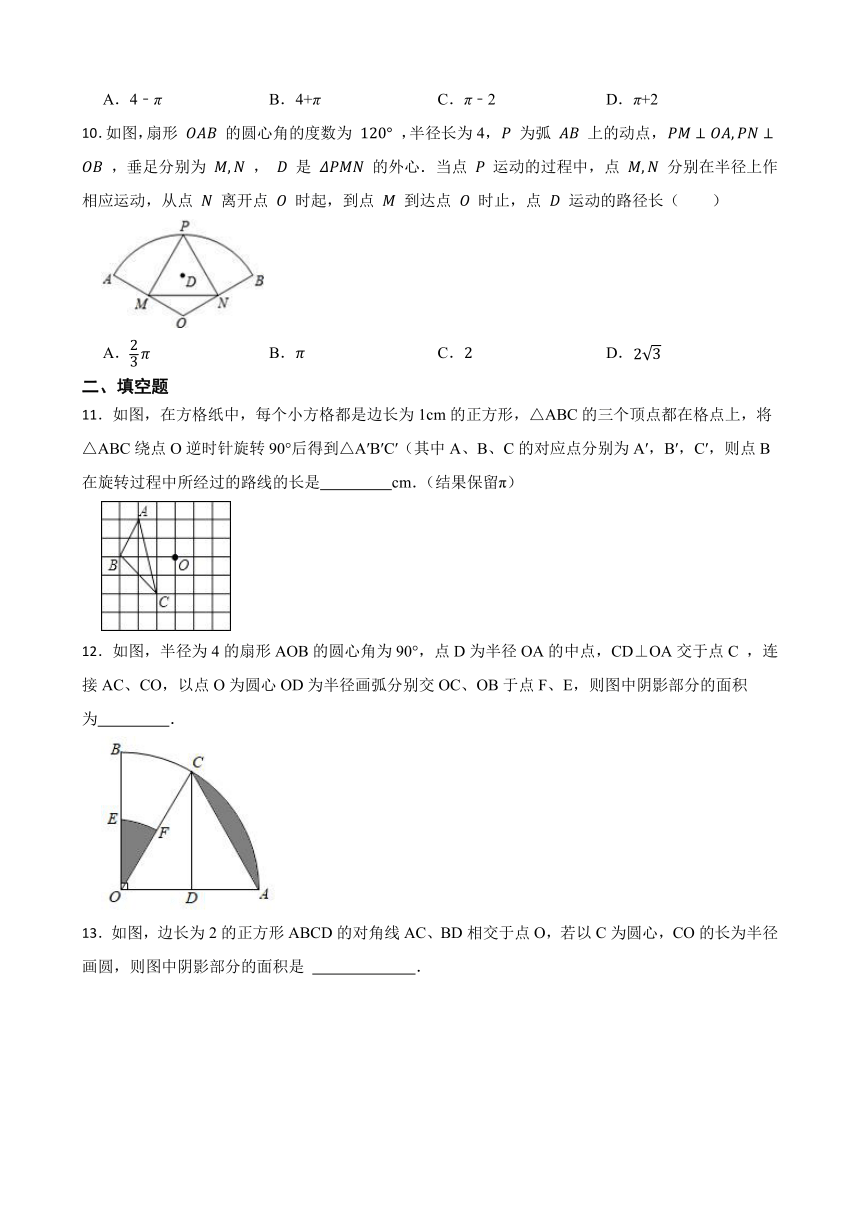
文档简介
浙教版初中数学九年级上册3.8弧长及扇形的面积----课后练习
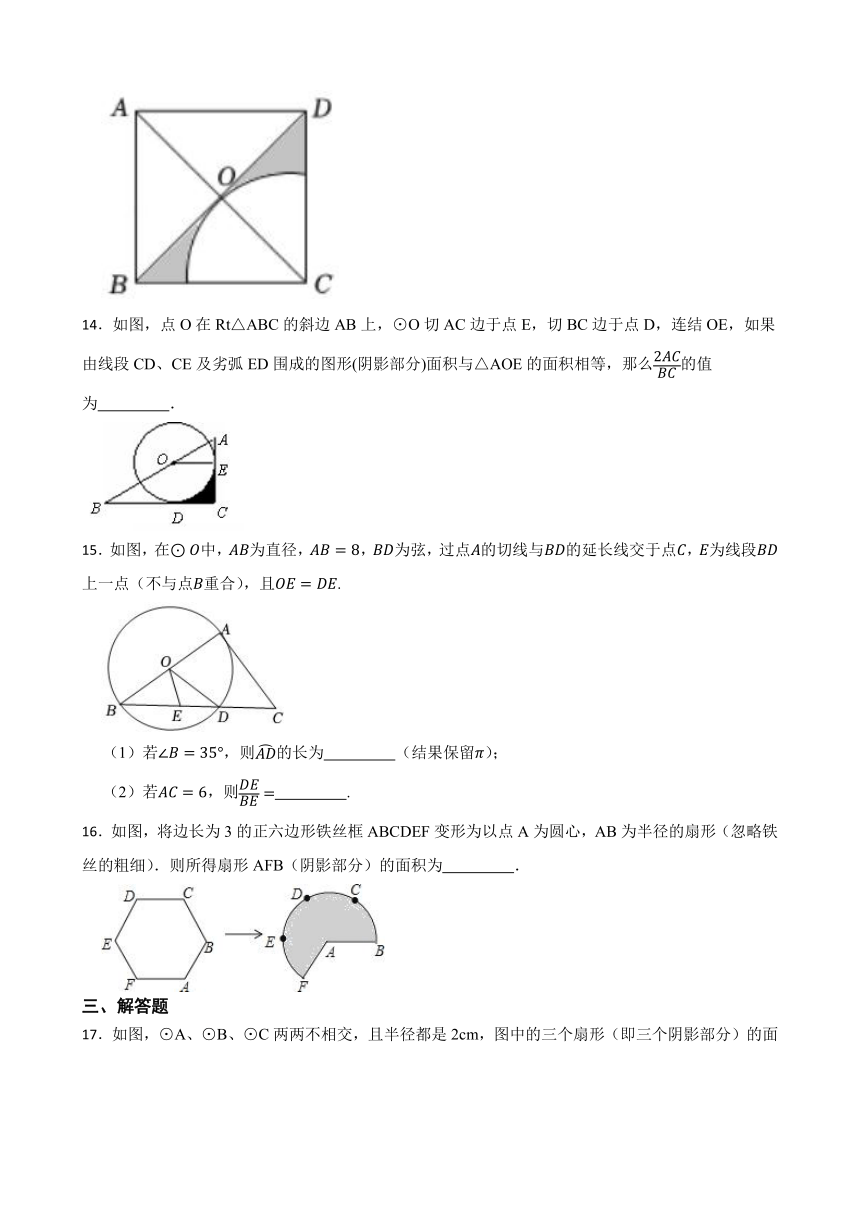
一、单选题
1.如图,在△ABC中,AB=AC=5,CB=8,分别以AB、AC为直径作半圆,则图中阴影部分面积是( )
A. B. C. D.
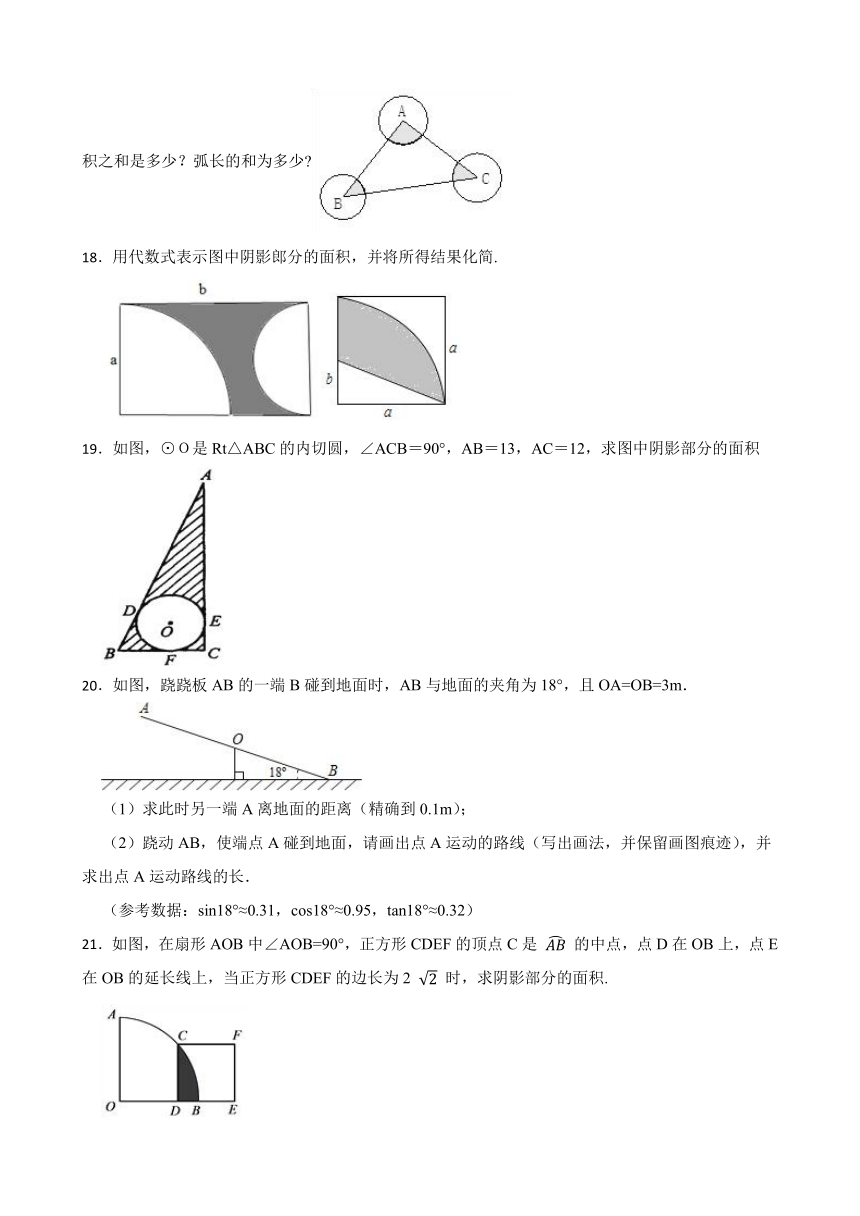
2.如图,菱形ABCD中,∠B=70°,AB=3,以AD为直径的⊙O交CD于点E,则弧DE的长为( )
A. π B. π C. π D. π
3.如图一个扇形纸片的圆心角为90°,半径为4,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,则图中阴影部分的面积为( )
A. B. C. D.
4.如图,扇形折扇完全打开后,如果张开的角度(∠BAC)为120°,骨柄AB的长为30cm,扇面的宽度BD的长为20cm,那么这把折扇的扇面面积为( )
A.cm2 B.cm2 C.cm2 D.300πcm2
5.某扇形的面积为12πcm2,圆心角为120°,则该扇形的半径是( )
A.3cm B.4cm C.5cm D.6cm
6.如图,把一张圆形纸片和一张含45°角的扇形纸片如图所示的方式分别剪得一个正方形,如果所剪得的两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )
A.4:5 B.2:5 C. :2 D. :
7.如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于E,交AC于F,点P是⊙A上一点,且∠EPF=40°,则图中阴影部分的面积是( )
A. B. C. D.
8.如图, ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则 的长为( )
A. π B. π C. π D. π
9.如图,在半径为2的⊙O中,将劣弧AB沿弦AB翻折,折叠后的弧AB恰好与OA、OB相切,则阴影部分的面积为( ).
A.4﹣π B.4+π C.π﹣2 D.π+2
10.如图,扇形 的圆心角的度数为 ,半径长为4, 为弧 上的动点, ,垂足分别为 , 是 的外心.当点 运动的过程中,点 分别在半径上作相应运动,从点 离开点 时起,到点 到达点 时止,点 运动的路径长( )
A. B. C. D.
二、填空题
11.如图,在方格纸中,每个小方格都是边长为1cm的正方形,△ABC的三个顶点都在格点上,将△ABC绕点O逆时针旋转90°后得到△A′B′C′(其中A、B、C的对应点分别为A′,B′,C′,则点B在旋转过程中所经过的路线的长是 cm.(结果保留π)
12.如图,半径为4的扇形AOB的圆心角为90°,点D为半径OA的中点,CD⊥OA交于点C ,连接AC、CO,以点O为圆心OD为半径画弧分别交OC、OB于点F、E,则图中阴影部分的面积为 .
13.如图,边长为2的正方形ABCD的对角线AC、BD相交于点O,若以C为圆心,CO的长为半径画圆,则图中阴影部分的面积是 .
14.如图,点O在Rt△ABC的斜边AB上,⊙O切AC边于点E,切BC边于点D,连结OE,如果由线段CD、CE及劣弧ED围成的图形(阴影部分)面积与△AOE的面积相等,那么的值为 .
15.如图,在中,为直径,,为弦,过点的切线与的延长线交于点,为线段上一点(不与点重合),且.
(1)若,则的长为 (结果保留);
(2)若,则 .
16.如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为 .
三、解答题
17.如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,图中的三个扇形(即三个阴影部分)的面积之和是多少?弧长的和为多少
18.用代数式表示图中阴影郎分的面积,并将所得结果化简.
19.如图,⊙O是Rt△ABC的内切圆,∠ACB=90°,AB=13,AC=12,求图中阴影部分的面积
20.如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为18°,且OA=OB=3m.
(1)求此时另一端A离地面的距离(精确到0.1m);
(2)跷动AB,使端点A碰到地面,请画出点A运动的路线(写出画法,并保留画图痕迹),并求出点A运动路线的长.
(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
21.如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2 时,求阴影部分的面积.
22.如图,在边长为1的小正方形构成的网格中,点 , 在格点上,连接 ,作线段 关于直线 的对称线段 ,在直线 上取一格点 ,连接 , , , , .
(1)求证: ≌ ;
(2)求以点 为圆心的劣弧 的长.
23.制造弯形管道时,经常要先按中心线计算“展直长度”,再备料.下图是一段管道,其中直管道部分AB的长为3 000mm,弯形管道部分BC,CD弧的半径都是1 000mm,∠O=∠O’=90°,计算图中中心虚线的长度.
24.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(顶点是网格线的交点)
(1)先将△ABC竖直向上平移5个单位,再水平向右平移4个单位得到△A1B1C1,请画出△A1B1C1;
(2)将△A1B1C1绕B1点顺时针旋转90°,得△A2B1C2,请画出△A2B1C2;
(3)求线段B1C1变换到B1C2的过程中扫过区域的面积.
答案解析部分
1.【答案】D
2.【答案】A
3.【答案】B
4.【答案】C
5.【答案】D
6.【答案】A
7.【答案】A
8.【答案】B
9.【答案】A
10.【答案】A
11.【答案】 π
12.【答案】
13.【答案】2-π
14.【答案】4﹣π
15.【答案】(1)
(2)
16.【答案】18
17.【答案】三角形的内角和为180°,刚好为三个圆的圆心角,由圆心角=弧长与半径的比,可得弧长=;
三个圆的圆心角和为180°,相当于半圆;而圆的面积=,所以半圆面积为
18.【答案】解: = = = ;
= .
19.【答案】解:设圆半径为R
在Rt△ABC中,BC =AB -AC =13 -12 =25
∴BC=5
S△ABC=1/2(BC×AC)=1/2(5×12)=30
设圆心点为O,做OE⊥AB交AB于E,OF⊥BC交BC于F,OG⊥AC交AC于G
则OE=OF=OG=R
S△ABC=S△ABO+S△BCO+S△CAO=1/2(AB*R)+1/2(BC*R)+1/2(AC*R)
=1/2(AB+BC+AC)*R
=15R
S△ABC=30
∴R=2
∴圆的面积为3.14×2 =12.56
∴此三角形减去内切圆的面积为30-12.56=17.44。
20.【答案】(1)答案
解:过点A作地面的垂线,垂足为C,
在Rt△ABC中,∠ABC=18°,
∴AC=AB sin∠ABC
=6 sin18°
≈6×0.31≈1.9.
答:另一端A离地面的距离约为1.9 m.
;答案
解:过点A作地面的垂线,垂足为C,
在Rt△ABC中,∠ABC=18°,
∴AC=AB sin∠ABC
=6 sin18°
≈6×0.31≈1.9.
答:另一端A离地面的距离约为1.9 m.
;答案;解:过点A作地面的垂线,垂足为C,
在Rt△ABC中,∠ABC=18°,
∴AC=AB sin∠ABC
=6 sin18°
≈6×0.31≈1.9.
答:另一端A离地面的距离约为1.9 m.
(2)解:画法:以点O为圆心,OA长为半径画弧,交地面于点D,则 弧AD就是端点A运动的路线.
端点A运动路线的长为 (m).
答:端点A运动路线的长为 m.
21.【答案】解:∵在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是 的中点,
∴∠COD=45°,
∴OC= =4,
∴S阴影=S扇形BOC﹣S△ODC= ×π×42﹣ ×(2 )2
=2π﹣4
22.【答案】(1)证明:∵线段 与线段 关于直线 对称,
∴点 , 分别与点 , 关于直线 对称, .
∴直线 垂直平分 , .
∴ , .
∴ ≌ (SSS).
(2)解:如图,∵ , ,
∴ .
∴ 是直角三角形.∴ .
∴劣弧 的长为 .
23.【答案】解: ,
中心虚线的长度为
24.【答案】(1)解:如图所示:△A1B1C1,即为所求
(2)解:如图所示:△A2B1C2即为所求。
(3)解:线段B1C1变换到B1C2的过程中扫过区域的面积为: = π.
一、单选题
1.如图,在△ABC中,AB=AC=5,CB=8,分别以AB、AC为直径作半圆,则图中阴影部分面积是( )
A. B. C. D.
2.如图,菱形ABCD中,∠B=70°,AB=3,以AD为直径的⊙O交CD于点E,则弧DE的长为( )
A. π B. π C. π D. π
3.如图一个扇形纸片的圆心角为90°,半径为4,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,则图中阴影部分的面积为( )
A. B. C. D.
4.如图,扇形折扇完全打开后,如果张开的角度(∠BAC)为120°,骨柄AB的长为30cm,扇面的宽度BD的长为20cm,那么这把折扇的扇面面积为( )
A.cm2 B.cm2 C.cm2 D.300πcm2
5.某扇形的面积为12πcm2,圆心角为120°,则该扇形的半径是( )
A.3cm B.4cm C.5cm D.6cm
6.如图,把一张圆形纸片和一张含45°角的扇形纸片如图所示的方式分别剪得一个正方形,如果所剪得的两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )
A.4:5 B.2:5 C. :2 D. :
7.如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于E,交AC于F,点P是⊙A上一点,且∠EPF=40°,则图中阴影部分的面积是( )
A. B. C. D.
8.如图, ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则 的长为( )
A. π B. π C. π D. π
9.如图,在半径为2的⊙O中,将劣弧AB沿弦AB翻折,折叠后的弧AB恰好与OA、OB相切,则阴影部分的面积为( ).
A.4﹣π B.4+π C.π﹣2 D.π+2
10.如图,扇形 的圆心角的度数为 ,半径长为4, 为弧 上的动点, ,垂足分别为 , 是 的外心.当点 运动的过程中,点 分别在半径上作相应运动,从点 离开点 时起,到点 到达点 时止,点 运动的路径长( )
A. B. C. D.
二、填空题
11.如图,在方格纸中,每个小方格都是边长为1cm的正方形,△ABC的三个顶点都在格点上,将△ABC绕点O逆时针旋转90°后得到△A′B′C′(其中A、B、C的对应点分别为A′,B′,C′,则点B在旋转过程中所经过的路线的长是 cm.(结果保留π)
12.如图,半径为4的扇形AOB的圆心角为90°,点D为半径OA的中点,CD⊥OA交于点C ,连接AC、CO,以点O为圆心OD为半径画弧分别交OC、OB于点F、E,则图中阴影部分的面积为 .
13.如图,边长为2的正方形ABCD的对角线AC、BD相交于点O,若以C为圆心,CO的长为半径画圆,则图中阴影部分的面积是 .
14.如图,点O在Rt△ABC的斜边AB上,⊙O切AC边于点E,切BC边于点D,连结OE,如果由线段CD、CE及劣弧ED围成的图形(阴影部分)面积与△AOE的面积相等,那么的值为 .
15.如图,在中,为直径,,为弦,过点的切线与的延长线交于点,为线段上一点(不与点重合),且.
(1)若,则的长为 (结果保留);
(2)若,则 .
16.如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为 .
三、解答题
17.如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,图中的三个扇形(即三个阴影部分)的面积之和是多少?弧长的和为多少
18.用代数式表示图中阴影郎分的面积,并将所得结果化简.
19.如图,⊙O是Rt△ABC的内切圆,∠ACB=90°,AB=13,AC=12,求图中阴影部分的面积
20.如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为18°,且OA=OB=3m.
(1)求此时另一端A离地面的距离(精确到0.1m);
(2)跷动AB,使端点A碰到地面,请画出点A运动的路线(写出画法,并保留画图痕迹),并求出点A运动路线的长.
(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
21.如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2 时,求阴影部分的面积.
22.如图,在边长为1的小正方形构成的网格中,点 , 在格点上,连接 ,作线段 关于直线 的对称线段 ,在直线 上取一格点 ,连接 , , , , .
(1)求证: ≌ ;
(2)求以点 为圆心的劣弧 的长.
23.制造弯形管道时,经常要先按中心线计算“展直长度”,再备料.下图是一段管道,其中直管道部分AB的长为3 000mm,弯形管道部分BC,CD弧的半径都是1 000mm,∠O=∠O’=90°,计算图中中心虚线的长度.
24.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(顶点是网格线的交点)
(1)先将△ABC竖直向上平移5个单位,再水平向右平移4个单位得到△A1B1C1,请画出△A1B1C1;
(2)将△A1B1C1绕B1点顺时针旋转90°,得△A2B1C2,请画出△A2B1C2;
(3)求线段B1C1变换到B1C2的过程中扫过区域的面积.
答案解析部分
1.【答案】D
2.【答案】A
3.【答案】B
4.【答案】C
5.【答案】D
6.【答案】A
7.【答案】A
8.【答案】B
9.【答案】A
10.【答案】A
11.【答案】 π
12.【答案】
13.【答案】2-π
14.【答案】4﹣π
15.【答案】(1)
(2)
16.【答案】18
17.【答案】三角形的内角和为180°,刚好为三个圆的圆心角,由圆心角=弧长与半径的比,可得弧长=;
三个圆的圆心角和为180°,相当于半圆;而圆的面积=,所以半圆面积为
18.【答案】解: = = = ;
= .
19.【答案】解:设圆半径为R
在Rt△ABC中,BC =AB -AC =13 -12 =25
∴BC=5
S△ABC=1/2(BC×AC)=1/2(5×12)=30
设圆心点为O,做OE⊥AB交AB于E,OF⊥BC交BC于F,OG⊥AC交AC于G
则OE=OF=OG=R
S△ABC=S△ABO+S△BCO+S△CAO=1/2(AB*R)+1/2(BC*R)+1/2(AC*R)
=1/2(AB+BC+AC)*R
=15R
S△ABC=30
∴R=2
∴圆的面积为3.14×2 =12.56
∴此三角形减去内切圆的面积为30-12.56=17.44。
20.【答案】(1)答案
解:过点A作地面的垂线,垂足为C,
在Rt△ABC中,∠ABC=18°,
∴AC=AB sin∠ABC
=6 sin18°
≈6×0.31≈1.9.
答:另一端A离地面的距离约为1.9 m.
;答案
解:过点A作地面的垂线,垂足为C,
在Rt△ABC中,∠ABC=18°,
∴AC=AB sin∠ABC
=6 sin18°
≈6×0.31≈1.9.
答:另一端A离地面的距离约为1.9 m.
;答案;解:过点A作地面的垂线,垂足为C,
在Rt△ABC中,∠ABC=18°,
∴AC=AB sin∠ABC
=6 sin18°
≈6×0.31≈1.9.
答:另一端A离地面的距离约为1.9 m.
(2)解:画法:以点O为圆心,OA长为半径画弧,交地面于点D,则 弧AD就是端点A运动的路线.
端点A运动路线的长为 (m).
答:端点A运动路线的长为 m.
21.【答案】解:∵在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是 的中点,
∴∠COD=45°,
∴OC= =4,
∴S阴影=S扇形BOC﹣S△ODC= ×π×42﹣ ×(2 )2
=2π﹣4
22.【答案】(1)证明:∵线段 与线段 关于直线 对称,
∴点 , 分别与点 , 关于直线 对称, .
∴直线 垂直平分 , .
∴ , .
∴ ≌ (SSS).
(2)解:如图,∵ , ,
∴ .
∴ 是直角三角形.∴ .
∴劣弧 的长为 .
23.【答案】解: ,
中心虚线的长度为
24.【答案】(1)解:如图所示:△A1B1C1,即为所求
(2)解:如图所示:△A2B1C2即为所求。
(3)解:线段B1C1变换到B1C2的过程中扫过区域的面积为: = π.
同课章节目录
