第1章《二次函数》单元测试卷 含解析
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版2022年九年级上册第1章《二次函数》单元测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列各式中,y是x的二次函数的是( )
A.y=3x B.y=x2+(3﹣x)x
C.y=(x﹣1)2 D.y=ax2+bx+c
2.抛物线y=﹣3(x﹣4)2+1的顶点坐标( )
A.(﹣4,1) B.(﹣4,﹣1) C.(4,﹣1) D.(4,1)
3.下列各函数中,y随x的增大而减小的函数是( )
A. B.y=﹣x C.y=x2 D.y=﹣x2
4.在平面直角坐标系中,将二次函数y=2x2的图象向左平移5个单位,所得图象的解析式为( )
A.y=2x2﹣5 B.y=2x2+5 C.y=2(x﹣5)2 D.y=2(x+5)2
5.抛物线y=2x2﹣4x+c经过三点(﹣3,y1),(﹣1,y2),(2,y3),则y1,y2,y3的大小关系是( )
A.y2>y3>y1 B.y1>y2>y3 C.y2>y1>y3 D.y1>y3>y2
6.已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且当﹣2≤x≤1时,y的最大值为9,则a的值为( )
A.﹣1 B.1 C.﹣2 D.2
7.一次函数y=ax+b(a≠0)与二次函数y=ax2+bx(a≠0)在同一平面直角坐标系中的图象可能是( )
A. B. C. D.
8.已知二次函数y=ax2+bx+c的自变量x与函数值y的部分对应值如表:则关于x的一元二次方程ax2+bx+c0的解是( )
x … ﹣1 0 1 2 3 …
y … 3 0 ﹣1 m 3 …
A.x1=0,x2=2 B.x1=x2=2 C.x1=x2=0 D.不能确定
9.如图,正方形的四个顶点坐标依次为(1,﹣1),(3,﹣1)(3,﹣3),(1,﹣3),若抛物线y=ax2的图象与正方形有公共点,则实数a的取值范围是( )
A.﹣3≤a≤﹣ B.≤a≤3 C.≤a≤1 D.﹣1≤a≤﹣
10.如图为二次函数y=ax2+bx+c的图象,给出下列说法:①a<0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;③a+b+c>0;④当x>1时,y随x值的增大而增大;⑤当y>0时,x<﹣1,或x>3.其中,正确的说法有( )
A.①②④ B.①②⑤ C.①③⑤ D.②④⑤
二.填空题(共6小题,满分18分,每小题3分)
11.抛物线y=﹣x2+2kx+2与坐标轴交点的个数为 .
12.抛物线y=x2+bx+c的图象上有两点A(1,m),B(5,m),则b的值为 .
13.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的函数表达式为y=ax2+bx+c(a≠0),若此炮弹在第6秒与第13秒时的高度相等,则炮弹所在高度最高的是第 秒.
14.已知二次函数y=﹣x2+4x﹣3,当1≤x≤a时,函数y的最小值为﹣2,则a的值为 .
15.抛物线y=ax2+bx+c(a,b,c为常数)的部分图象如图所示,设m=4a﹣2b+c,则m的取值范围是 .
16.如图,抛物线y=﹣x2+bx+c与y轴交于A点,与x轴交于B、C两点,B(﹣1,0),C
(3,0),连接AC,将线段AC向上平移落在EF处,且EF恰好经过这个抛物线的顶点D,则四边形ACFE的周长为 .
三.解答题(共7小题,满分52分)
17.(6分)已知函数y=kx2﹣(2k+3)x+3k+1.
(1)当k=1时,求函数y=kx2﹣(2k+3)x+3k+1的顶点坐标,与x轴的交点坐标;
(2)若当x≥0时,函数y随x的增大而减小,求k的取值范围.
18.(7分)已知二次函数y=x2+2x﹣3.
(1)用配方法把这个二次函数化成y=a(x﹣h)2+k的形式;
(2)在所给的平面直角坐标系中,画出这个二次函数的图象;
(3)当﹣4≤x≤0时,结合图象直接写出y的取值范围.
19.(7分)如图,学校要用一段长为32米的篱笆围成一个一边靠墙的矩形花圃,墙长为14米.
(1)若矩形ABCD的面积为96平方米,求矩形的边AB的长.
(2)要想使花圃的面积最大,AB边的长应为多少米?最大面积为多少平方米?
20.(7分)某商店购进了一种消毒用品,进价为每件8元,在销售过程中发现,每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中8≤x≤15,且x为整数).当每件消毒用品售价为9元时,每天的销售量为105件;当每件消毒用品售价为11元时,每天的销售量为95件.
(1)求y与x之间的函数关系式;
(2)设该商店销售这种消毒用品每天获利w(元),当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?
21.(8分)有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为12m.现将它的图形放在如图所示的直角坐标系中.
(1)求这条抛物线的解析式.
(2)一艘宽为4米,高出水面3米的货船,能否从桥下通过?
22.(8分)如图,已知抛物线y=ax2+bx+c的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.若点P是线段BC上的动点,过点P作直线PM∥y轴,交抛物线于点M.求线段PM的最大值.
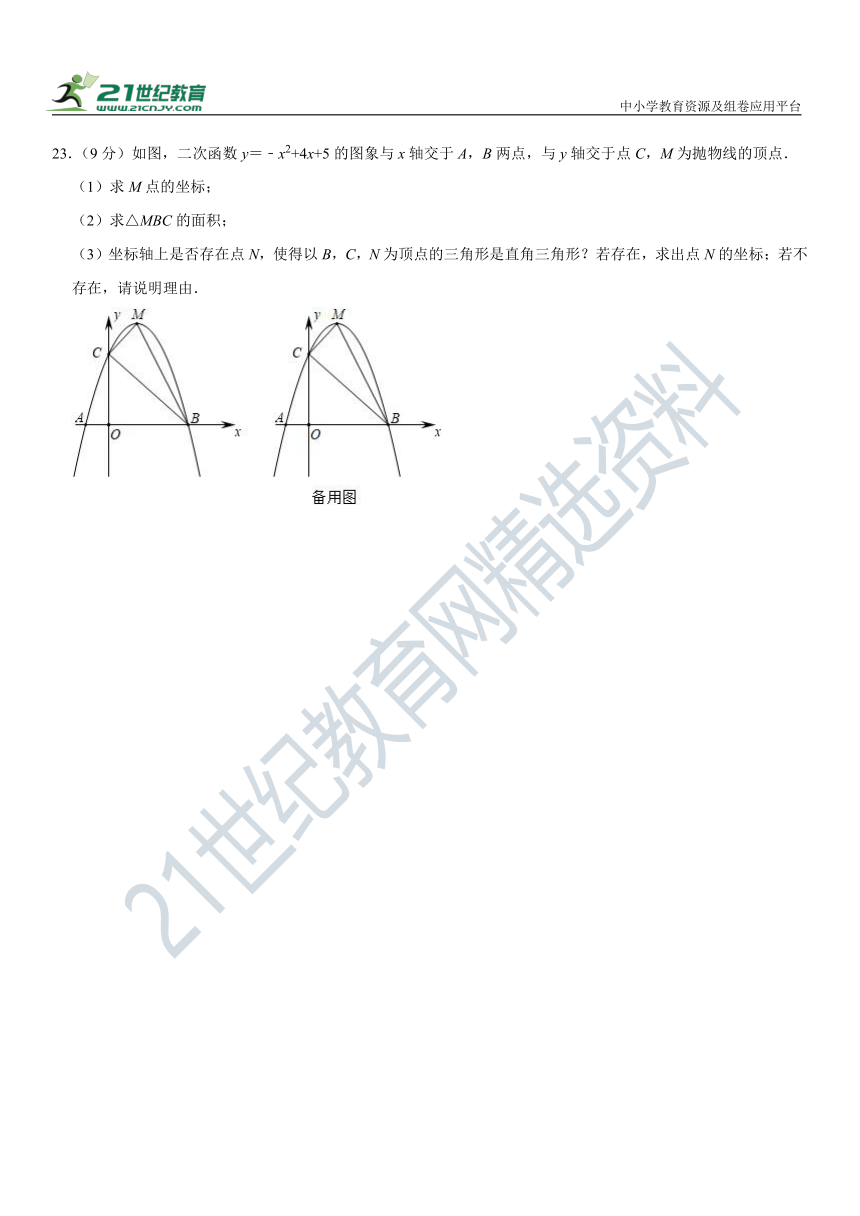
23.(9分)如图,二次函数y=﹣x2+4x+5的图象与x轴交于A,B两点,与y轴交于点C,M为抛物线的顶点.
(1)求M点的坐标;
(2)求△MBC的面积;
(3)坐标轴上是否存在点N,使得以B,C,N为顶点的三角形是直角三角形?若存在,求出点N的坐标;若不存在,请说明理由.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:A.y是x的一次函数,不是二次函数,故本选项不符合题意;
B.y=x2+(3﹣x)x
=x2+3x﹣x2
=3x,y是x的一次函数,不是二次函数,故本选项不符合题意;
C.y是x的二次函数,故本选项符合题意;
D.当a=0时,y不是x的二次函数,故本选项不符合题意;
故选:C.
2.解:∵y=﹣3(x﹣4)2+1,
∴抛物线开口向下,顶点坐标为(4,1),
故选:D.
3.解:A、是一次函数,∵k=>0,∴y随x的增大而增大,故该选项不符合题意;
B、是一次函数,∵k=﹣1<0,∴y随x的增大而减小,故该选项符合题意;
C、是二次函数,开口向上,对称轴是y轴,∴当x<0时,y随x的增大而减小,故该选项不符合题意;
D、是二次函数,开口向下,对称轴是y轴,∴当x>0时,y随x的增大而减小,故该选项不符合题意.
故选:B.
4.解:原抛物线的顶点为(0,0),向左平移5个单位,那么新抛物线的顶点为(﹣5,0);
可设新抛物线的解析式为y=2(x﹣h)2+k,代入得:y=2(x+5)2.
故选:D.
5.解:∵y=2x2﹣4x+c,
∴抛物线开口向上,对称轴为直线x=﹣=2,
∴x≤2时,y随x增大而减小,
∴y1>y2>y3.
故选:B.
6.解:∵二次函数y=ax2+2ax+3a2+3=a(x+1)2+3a2﹣a+3(其中x是自变量),
∴该函数的对称轴为直线x=﹣1,
∵当x≥2时,y随x的增大而增大,
∴a>0,
又∵当﹣2≤x≤1时,y的最大值为9,
∴x=1时,y=9,
即9=a(1+1)2+3a2﹣a+3,
解得,a1=﹣2(舍去),a2=1,
由上可得,a的值是1,
故选:B.
7.解:
解得或.
故二次函数y=ax2+bx与一次函数y=ax+b(a≠0)在同一平面直角坐标系中的交点在x轴上或点(1,a+b).
故选:C.
8.解:函数y=ax2+bx+c的图象与x轴的交点就是方程ax2+bx+c=0的根,函数y=ax2+bx+c的图象与x轴的交点的纵坐标为0.
由表中数据可知:x=﹣1和x=3的函数值相同,都是3,
∴二次函数y=ax2+bx+c的对称轴为直线x==1,
∴点(0,0)的对称点为(2,0),
∴关于x的一元二次方程ax2+bx+c=0的解是x1=0,x2=2,
故选:A.
9.解:抛物线的解析式为y=ax2,
当抛物线经过(1,﹣3)时,a=﹣3,
当抛物线经过(3,﹣1)时,a=﹣,
观察图象可知﹣3≤a≤﹣,
故选:A.
10.解:①∵抛物线开口向上,
∴a>0,故①错误;
②由图可得,二次函数y=ax2+bx+c的图象与x轴交于(﹣1,0)(3,0).
∴方程ax2+bx+c=0的根为x1=﹣1,x2=3,故②正确;
③∵二次函数y=ax2+bx+c的图象与x轴交于(﹣1,0)(3,0),
∴抛物线对称轴为x==1.
当x=1时,y=a+b+c<0.故③错误;
④∵抛物线对称轴是直线x=1,
∴在对称轴右侧y随x的增大而增大,
即当x>1时,y随x的增大而增大.故④正确;
⑤由图可知,当y>0时,则抛物线在x轴上方的部分,
在对称轴的左侧对应的x值为,x<﹣1,
在对称轴右侧对应的x值为x>3.
∴当y>0时,x<﹣1,或x>3.故⑤正确.
综上所述,正确的有②④⑤.
故选:D.
二.填空题(共6小题,满分18分,每小题3分)
11.解:a=﹣1,b=2k,c=2,
∵b2﹣4ac=4k2+8>0,
∴抛物线y=﹣x2+2kx+2与x轴交点的个数为2,
∵抛物线y=﹣x2+2kx+2与y轴交点的个数为1,
∴抛物线y=﹣x2+2kx+2与坐标轴交点的个数为3;
故答案为:3.
12.解:∵抛物线经过A(1,m),B(5,m),
∴抛物线对称轴为直线x=3,
∴﹣=3,
解得b=﹣6,
故答案为:﹣6.
13.解:∵此炮弹在第6与第13秒时的高度相等,
∴抛物线的对称轴是:x==9.5,
∴炮弹所在高度最高是第9.5秒,
故答案为:9.5.
14.解:∵y=﹣x2+4x﹣3=﹣(x﹣2)2+1,
∴抛物线开口向下,对称轴为直线x=2,顶点坐标为(2,1),
∴y≤1,
将x=1代入y=﹣x2+4x﹣3得y=0>﹣2,
∴x=a时,y=﹣2,
∴﹣2=﹣a2+4a﹣3,
解得a=2﹣(舍)或a=2+.
故答案为:2+.
15.解:∵抛物线开口向上,
∴a>0,
∵抛物线对称轴在y轴左侧,
∴﹣<0,
∴b>0,
∵抛物线经过(0,﹣2),
∴c=﹣2,
∵抛物线经过(1,0),
∴a+b+c=0,
∴a+b=2,b=2﹣a,
∴m=4a﹣2b+c=4a﹣2(2﹣a)+(﹣2)=6a﹣6,
∴y=ax2+(2﹣a)x﹣2,
当x=﹣2时,y=4a﹣2(2﹣a)+(﹣2)=6a﹣6,
∵b=2﹣a>0,
∴0<a<2,
∴﹣6<6a﹣6<6,
故答案为:﹣6<m<6.
16.解:∵抛物线y=﹣x2+bx+c与x轴交于B(﹣1,0)和C(3,0),
∴抛物线解析式为y=﹣(x+1)(x﹣3),
即y=﹣x2+2x+3;
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D的坐标为(1,4),
当x=0时,y=﹣x2+2x+3=3,则A(0,3),
∴AC==3,
设直线AC的解析式为y=mx+n,
把A(0,3),C(3,0)分别代入得,
解得,
∴直线AC的解析式为y=﹣x+3,
∵线段AC向上平移得到EF,
∴EF∥AC,EF=AC,
∴四边形ACFE为平行四边形,
设直线EF的解析式为y=﹣x+q,
把D(1,4)代入得4=﹣1+q,
解得q=5,
∴直线EF的解析式为y=﹣x+5,
当x=0时,y=﹣x+5=5,则E(0,5),
∴AE=5﹣3=2,
∴四边形ACFE的周长=2(2+3)=4+6.
故答案为:4+6.
三.解答题(共7小题,满分52分)
17.解:(1)当k=1时,y=x2﹣5x+4=(x﹣)2﹣,
∴抛物线顶点坐标为(,﹣),
在y=x2﹣5x+4中,令y=0得:
x2﹣5x+4=0,
解得x1=1,x2=4,
∴抛物线与x轴交点为(1,0),(4,0);
(2)①当k=0时,y=﹣3x+1,
∵﹣3<0,
∴y随x增大而减小,
∴当x≥0时,函数y随x的增大而减小成立;
②当k≠0时,
∵当x≥0时,函数y=kx2﹣(2k+3)x+3k+1随x的增大而减小,
∴抛物线开口向下,对称轴是y轴或在y轴左侧,
∴,
解得﹣≤k<0,
综上所述,当x≥0时,函数y=kx2﹣(2k+3)x+3k+1随x的增大而减小,k的范围是﹣≤k≤0.
18.解:(1)y=x2+2x﹣3=x2+2x+1﹣4=(x+1)2﹣4,
即y=(x+1)2﹣4;
(2)∵y=(x+1)2﹣4,
∴顶点坐标为(﹣1,﹣4),
当y=0时,x2+2x﹣3=0,
解得:x1=1,x2=﹣3,
∴抛物线与x轴的交点坐标为(﹣3,0),(1,0),
当x=0时,y=﹣3,
∴抛物线与y轴的交点坐标为(0,﹣3),
二次函数的图象如图所示:
(3)观察图象得,当x=﹣1时,y取最小值﹣4,
当x=﹣4时,y取最大值,代入函数得,y=(﹣4)2+2×(﹣4)﹣3=16﹣8﹣3=5.
∴当﹣4≤x≤0时,﹣4≤y≤5.
19.解:(1)设AB为x米,则BC=(36﹣2x)米,
由题意得:x(32﹣2x)=96,
解得:x1=4,x2=12,
∵墙长为14米,32米的篱笆,
∴32﹣2x≤14,2x<32,
∴9≤x<16,
∴x=12,
∴AB=12,
答:矩形的边AB的长为12米;
(2)设AB为x米,矩形的面积为y平方米,则BC=(32﹣2x)米,
∴y=x(32﹣2x)=﹣2x2+32x=﹣2(x﹣8)2+128,
∵9≤x<16,且﹣2<0,故抛物线开口向下,
∴当x=9时,y有最大值是126,
答:AB边的长应为9米时,有最大面积,且最大面积为126平方米.
20.解:(1)设每天的销售量y(件)与每件售价x(元)函数关系式为:y=kx+b,
由题意可知:,
解得:,
∴y与x之间的函数关系式为:y=﹣5x+150;
(2)w=y(x﹣8)
=(﹣5x+150)(x﹣8)
=﹣5x2+190x﹣1200
=﹣5(x﹣19)2+605,
∵8≤x≤15,且x为整数,
∴当x<19时,w随x的增大而增大,
∴当x=15时,w有最大值,最大值为﹣5×(15﹣19)2+605=525.
答:每件消毒用品的售价为15元时,每天的销售利润最大,最大利润是525元.
21.解:(1)由图象可知,
抛物线的顶点坐标为(6,4),过点(12,0),
设抛物线的解析式为:y=a(x﹣6)2+4,
则0=a(12﹣6)2+4,
解得,a=﹣,
即这条抛物线的解析式为:y=﹣(x﹣6)2+4;
(2)当x=(12﹣4)=4时,y=﹣(4﹣6)2+4=>3,
∴货船能顺利通过此桥洞.
22.解:∵抛物线的对称轴为直线x=﹣1,抛物线与x轴的一个交点A的坐标(1,0),
∴抛物线与x轴的另一个交点B的坐标为(﹣3,0),
设抛物线解析式为y=a(x+3)(x﹣1),
把C(0,3)代入得a×3×(﹣1)=3,
解得a=﹣1,
∴抛物线解析式为y=﹣(x+3)(x﹣1),
即y=﹣x2﹣2x+3,
设直线BC的解析式为y=mx+n,
把B(﹣3,0),C(0,3)代入得,
解得,
∴直线BC的解析式为y=x+3,
设P(t,t+3)(﹣3<t<0),则M(t,﹣t2﹣2t+3),
∴PM=﹣t2﹣2t+3﹣(t+3)=﹣t2﹣3t,
∵PM=﹣(t+)2+,
∴当t=﹣时,PM有最大值,最大值为.
23.解:(1)y=﹣x2+4x+5=﹣(x﹣2)2+9,
∴M(2,9);
(2)令y=0,得﹣x2+4x+5=0,
解得 x=﹣1或x=5,
∴A(﹣1,0),B(5,0),
令x=0,得y=﹣x2+4x+5=5,
∴C(0,5),
过点M作ME⊥y轴于点E,
∴S△MBC=S四边形MBOE﹣S△MCE﹣S△BOC==15;
(3)存在点N,使得以B,C,N为顶点的三角形是直角三角形,理由如下:
∵OB=OC=5,∠COB=90°,
∴∠OCB=∠OBC=45°,
∴△BOC是等腰直角三角形,
①当C为直角顶点时,作CN1⊥BC交坐标轴为N1,∠CN1B=∠CBN1=45°,
∴OB=ON1=5,
∴N1(﹣5,0);
②当B为直角顶点时,作BN2⊥BC交坐标轴为N2,∠CN2B=∠BCN2=45°,
∴OC=ON2=5,
∴N1(0,﹣5);
③当N为直角顶点时,点O与N3重合,
∴N3(0,0).
综上所述,满足条件的点N的坐标为(﹣5,0)或(0,﹣5)或(0,0).
浙教版2022年九年级上册第1章《二次函数》单元测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列各式中,y是x的二次函数的是( )
A.y=3x B.y=x2+(3﹣x)x
C.y=(x﹣1)2 D.y=ax2+bx+c
2.抛物线y=﹣3(x﹣4)2+1的顶点坐标( )
A.(﹣4,1) B.(﹣4,﹣1) C.(4,﹣1) D.(4,1)
3.下列各函数中,y随x的增大而减小的函数是( )
A. B.y=﹣x C.y=x2 D.y=﹣x2
4.在平面直角坐标系中,将二次函数y=2x2的图象向左平移5个单位,所得图象的解析式为( )
A.y=2x2﹣5 B.y=2x2+5 C.y=2(x﹣5)2 D.y=2(x+5)2
5.抛物线y=2x2﹣4x+c经过三点(﹣3,y1),(﹣1,y2),(2,y3),则y1,y2,y3的大小关系是( )
A.y2>y3>y1 B.y1>y2>y3 C.y2>y1>y3 D.y1>y3>y2
6.已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且当﹣2≤x≤1时,y的最大值为9,则a的值为( )
A.﹣1 B.1 C.﹣2 D.2
7.一次函数y=ax+b(a≠0)与二次函数y=ax2+bx(a≠0)在同一平面直角坐标系中的图象可能是( )
A. B. C. D.
8.已知二次函数y=ax2+bx+c的自变量x与函数值y的部分对应值如表:则关于x的一元二次方程ax2+bx+c0的解是( )
x … ﹣1 0 1 2 3 …
y … 3 0 ﹣1 m 3 …
A.x1=0,x2=2 B.x1=x2=2 C.x1=x2=0 D.不能确定
9.如图,正方形的四个顶点坐标依次为(1,﹣1),(3,﹣1)(3,﹣3),(1,﹣3),若抛物线y=ax2的图象与正方形有公共点,则实数a的取值范围是( )
A.﹣3≤a≤﹣ B.≤a≤3 C.≤a≤1 D.﹣1≤a≤﹣
10.如图为二次函数y=ax2+bx+c的图象,给出下列说法:①a<0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;③a+b+c>0;④当x>1时,y随x值的增大而增大;⑤当y>0时,x<﹣1,或x>3.其中,正确的说法有( )
A.①②④ B.①②⑤ C.①③⑤ D.②④⑤
二.填空题(共6小题,满分18分,每小题3分)
11.抛物线y=﹣x2+2kx+2与坐标轴交点的个数为 .
12.抛物线y=x2+bx+c的图象上有两点A(1,m),B(5,m),则b的值为 .
13.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的函数表达式为y=ax2+bx+c(a≠0),若此炮弹在第6秒与第13秒时的高度相等,则炮弹所在高度最高的是第 秒.
14.已知二次函数y=﹣x2+4x﹣3,当1≤x≤a时,函数y的最小值为﹣2,则a的值为 .
15.抛物线y=ax2+bx+c(a,b,c为常数)的部分图象如图所示,设m=4a﹣2b+c,则m的取值范围是 .
16.如图,抛物线y=﹣x2+bx+c与y轴交于A点,与x轴交于B、C两点,B(﹣1,0),C
(3,0),连接AC,将线段AC向上平移落在EF处,且EF恰好经过这个抛物线的顶点D,则四边形ACFE的周长为 .
三.解答题(共7小题,满分52分)
17.(6分)已知函数y=kx2﹣(2k+3)x+3k+1.
(1)当k=1时,求函数y=kx2﹣(2k+3)x+3k+1的顶点坐标,与x轴的交点坐标;
(2)若当x≥0时,函数y随x的增大而减小,求k的取值范围.
18.(7分)已知二次函数y=x2+2x﹣3.
(1)用配方法把这个二次函数化成y=a(x﹣h)2+k的形式;
(2)在所给的平面直角坐标系中,画出这个二次函数的图象;
(3)当﹣4≤x≤0时,结合图象直接写出y的取值范围.
19.(7分)如图,学校要用一段长为32米的篱笆围成一个一边靠墙的矩形花圃,墙长为14米.
(1)若矩形ABCD的面积为96平方米,求矩形的边AB的长.
(2)要想使花圃的面积最大,AB边的长应为多少米?最大面积为多少平方米?
20.(7分)某商店购进了一种消毒用品,进价为每件8元,在销售过程中发现,每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中8≤x≤15,且x为整数).当每件消毒用品售价为9元时,每天的销售量为105件;当每件消毒用品售价为11元时,每天的销售量为95件.
(1)求y与x之间的函数关系式;
(2)设该商店销售这种消毒用品每天获利w(元),当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?
21.(8分)有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为12m.现将它的图形放在如图所示的直角坐标系中.
(1)求这条抛物线的解析式.
(2)一艘宽为4米,高出水面3米的货船,能否从桥下通过?
22.(8分)如图,已知抛物线y=ax2+bx+c的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.若点P是线段BC上的动点,过点P作直线PM∥y轴,交抛物线于点M.求线段PM的最大值.
23.(9分)如图,二次函数y=﹣x2+4x+5的图象与x轴交于A,B两点,与y轴交于点C,M为抛物线的顶点.
(1)求M点的坐标;
(2)求△MBC的面积;
(3)坐标轴上是否存在点N,使得以B,C,N为顶点的三角形是直角三角形?若存在,求出点N的坐标;若不存在,请说明理由.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:A.y是x的一次函数,不是二次函数,故本选项不符合题意;
B.y=x2+(3﹣x)x
=x2+3x﹣x2
=3x,y是x的一次函数,不是二次函数,故本选项不符合题意;
C.y是x的二次函数,故本选项符合题意;
D.当a=0时,y不是x的二次函数,故本选项不符合题意;
故选:C.
2.解:∵y=﹣3(x﹣4)2+1,
∴抛物线开口向下,顶点坐标为(4,1),
故选:D.
3.解:A、是一次函数,∵k=>0,∴y随x的增大而增大,故该选项不符合题意;
B、是一次函数,∵k=﹣1<0,∴y随x的增大而减小,故该选项符合题意;
C、是二次函数,开口向上,对称轴是y轴,∴当x<0时,y随x的增大而减小,故该选项不符合题意;
D、是二次函数,开口向下,对称轴是y轴,∴当x>0时,y随x的增大而减小,故该选项不符合题意.
故选:B.
4.解:原抛物线的顶点为(0,0),向左平移5个单位,那么新抛物线的顶点为(﹣5,0);
可设新抛物线的解析式为y=2(x﹣h)2+k,代入得:y=2(x+5)2.
故选:D.
5.解:∵y=2x2﹣4x+c,
∴抛物线开口向上,对称轴为直线x=﹣=2,
∴x≤2时,y随x增大而减小,
∴y1>y2>y3.
故选:B.
6.解:∵二次函数y=ax2+2ax+3a2+3=a(x+1)2+3a2﹣a+3(其中x是自变量),
∴该函数的对称轴为直线x=﹣1,
∵当x≥2时,y随x的增大而增大,
∴a>0,
又∵当﹣2≤x≤1时,y的最大值为9,
∴x=1时,y=9,
即9=a(1+1)2+3a2﹣a+3,
解得,a1=﹣2(舍去),a2=1,
由上可得,a的值是1,
故选:B.
7.解:
解得或.
故二次函数y=ax2+bx与一次函数y=ax+b(a≠0)在同一平面直角坐标系中的交点在x轴上或点(1,a+b).
故选:C.
8.解:函数y=ax2+bx+c的图象与x轴的交点就是方程ax2+bx+c=0的根,函数y=ax2+bx+c的图象与x轴的交点的纵坐标为0.
由表中数据可知:x=﹣1和x=3的函数值相同,都是3,
∴二次函数y=ax2+bx+c的对称轴为直线x==1,
∴点(0,0)的对称点为(2,0),
∴关于x的一元二次方程ax2+bx+c=0的解是x1=0,x2=2,
故选:A.
9.解:抛物线的解析式为y=ax2,
当抛物线经过(1,﹣3)时,a=﹣3,
当抛物线经过(3,﹣1)时,a=﹣,
观察图象可知﹣3≤a≤﹣,
故选:A.
10.解:①∵抛物线开口向上,
∴a>0,故①错误;
②由图可得,二次函数y=ax2+bx+c的图象与x轴交于(﹣1,0)(3,0).
∴方程ax2+bx+c=0的根为x1=﹣1,x2=3,故②正确;
③∵二次函数y=ax2+bx+c的图象与x轴交于(﹣1,0)(3,0),
∴抛物线对称轴为x==1.
当x=1时,y=a+b+c<0.故③错误;
④∵抛物线对称轴是直线x=1,
∴在对称轴右侧y随x的增大而增大,
即当x>1时,y随x的增大而增大.故④正确;
⑤由图可知,当y>0时,则抛物线在x轴上方的部分,
在对称轴的左侧对应的x值为,x<﹣1,
在对称轴右侧对应的x值为x>3.
∴当y>0时,x<﹣1,或x>3.故⑤正确.
综上所述,正确的有②④⑤.
故选:D.
二.填空题(共6小题,满分18分,每小题3分)
11.解:a=﹣1,b=2k,c=2,
∵b2﹣4ac=4k2+8>0,
∴抛物线y=﹣x2+2kx+2与x轴交点的个数为2,
∵抛物线y=﹣x2+2kx+2与y轴交点的个数为1,
∴抛物线y=﹣x2+2kx+2与坐标轴交点的个数为3;
故答案为:3.
12.解:∵抛物线经过A(1,m),B(5,m),
∴抛物线对称轴为直线x=3,
∴﹣=3,
解得b=﹣6,
故答案为:﹣6.
13.解:∵此炮弹在第6与第13秒时的高度相等,
∴抛物线的对称轴是:x==9.5,
∴炮弹所在高度最高是第9.5秒,
故答案为:9.5.
14.解:∵y=﹣x2+4x﹣3=﹣(x﹣2)2+1,
∴抛物线开口向下,对称轴为直线x=2,顶点坐标为(2,1),
∴y≤1,
将x=1代入y=﹣x2+4x﹣3得y=0>﹣2,
∴x=a时,y=﹣2,
∴﹣2=﹣a2+4a﹣3,
解得a=2﹣(舍)或a=2+.
故答案为:2+.
15.解:∵抛物线开口向上,
∴a>0,
∵抛物线对称轴在y轴左侧,
∴﹣<0,
∴b>0,
∵抛物线经过(0,﹣2),
∴c=﹣2,
∵抛物线经过(1,0),
∴a+b+c=0,
∴a+b=2,b=2﹣a,
∴m=4a﹣2b+c=4a﹣2(2﹣a)+(﹣2)=6a﹣6,
∴y=ax2+(2﹣a)x﹣2,
当x=﹣2时,y=4a﹣2(2﹣a)+(﹣2)=6a﹣6,
∵b=2﹣a>0,
∴0<a<2,
∴﹣6<6a﹣6<6,
故答案为:﹣6<m<6.
16.解:∵抛物线y=﹣x2+bx+c与x轴交于B(﹣1,0)和C(3,0),
∴抛物线解析式为y=﹣(x+1)(x﹣3),
即y=﹣x2+2x+3;
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D的坐标为(1,4),
当x=0时,y=﹣x2+2x+3=3,则A(0,3),
∴AC==3,
设直线AC的解析式为y=mx+n,
把A(0,3),C(3,0)分别代入得,
解得,
∴直线AC的解析式为y=﹣x+3,
∵线段AC向上平移得到EF,
∴EF∥AC,EF=AC,
∴四边形ACFE为平行四边形,
设直线EF的解析式为y=﹣x+q,
把D(1,4)代入得4=﹣1+q,
解得q=5,
∴直线EF的解析式为y=﹣x+5,
当x=0时,y=﹣x+5=5,则E(0,5),
∴AE=5﹣3=2,
∴四边形ACFE的周长=2(2+3)=4+6.
故答案为:4+6.
三.解答题(共7小题,满分52分)
17.解:(1)当k=1时,y=x2﹣5x+4=(x﹣)2﹣,
∴抛物线顶点坐标为(,﹣),
在y=x2﹣5x+4中,令y=0得:
x2﹣5x+4=0,
解得x1=1,x2=4,
∴抛物线与x轴交点为(1,0),(4,0);
(2)①当k=0时,y=﹣3x+1,
∵﹣3<0,
∴y随x增大而减小,
∴当x≥0时,函数y随x的增大而减小成立;
②当k≠0时,
∵当x≥0时,函数y=kx2﹣(2k+3)x+3k+1随x的增大而减小,
∴抛物线开口向下,对称轴是y轴或在y轴左侧,
∴,
解得﹣≤k<0,
综上所述,当x≥0时,函数y=kx2﹣(2k+3)x+3k+1随x的增大而减小,k的范围是﹣≤k≤0.
18.解:(1)y=x2+2x﹣3=x2+2x+1﹣4=(x+1)2﹣4,
即y=(x+1)2﹣4;
(2)∵y=(x+1)2﹣4,
∴顶点坐标为(﹣1,﹣4),
当y=0时,x2+2x﹣3=0,
解得:x1=1,x2=﹣3,
∴抛物线与x轴的交点坐标为(﹣3,0),(1,0),
当x=0时,y=﹣3,
∴抛物线与y轴的交点坐标为(0,﹣3),
二次函数的图象如图所示:
(3)观察图象得,当x=﹣1时,y取最小值﹣4,
当x=﹣4时,y取最大值,代入函数得,y=(﹣4)2+2×(﹣4)﹣3=16﹣8﹣3=5.
∴当﹣4≤x≤0时,﹣4≤y≤5.
19.解:(1)设AB为x米,则BC=(36﹣2x)米,
由题意得:x(32﹣2x)=96,
解得:x1=4,x2=12,
∵墙长为14米,32米的篱笆,
∴32﹣2x≤14,2x<32,
∴9≤x<16,
∴x=12,
∴AB=12,
答:矩形的边AB的长为12米;
(2)设AB为x米,矩形的面积为y平方米,则BC=(32﹣2x)米,
∴y=x(32﹣2x)=﹣2x2+32x=﹣2(x﹣8)2+128,
∵9≤x<16,且﹣2<0,故抛物线开口向下,
∴当x=9时,y有最大值是126,
答:AB边的长应为9米时,有最大面积,且最大面积为126平方米.
20.解:(1)设每天的销售量y(件)与每件售价x(元)函数关系式为:y=kx+b,
由题意可知:,
解得:,
∴y与x之间的函数关系式为:y=﹣5x+150;
(2)w=y(x﹣8)
=(﹣5x+150)(x﹣8)
=﹣5x2+190x﹣1200
=﹣5(x﹣19)2+605,
∵8≤x≤15,且x为整数,
∴当x<19时,w随x的增大而增大,
∴当x=15时,w有最大值,最大值为﹣5×(15﹣19)2+605=525.
答:每件消毒用品的售价为15元时,每天的销售利润最大,最大利润是525元.
21.解:(1)由图象可知,
抛物线的顶点坐标为(6,4),过点(12,0),
设抛物线的解析式为:y=a(x﹣6)2+4,
则0=a(12﹣6)2+4,
解得,a=﹣,
即这条抛物线的解析式为:y=﹣(x﹣6)2+4;
(2)当x=(12﹣4)=4时,y=﹣(4﹣6)2+4=>3,
∴货船能顺利通过此桥洞.
22.解:∵抛物线的对称轴为直线x=﹣1,抛物线与x轴的一个交点A的坐标(1,0),
∴抛物线与x轴的另一个交点B的坐标为(﹣3,0),
设抛物线解析式为y=a(x+3)(x﹣1),
把C(0,3)代入得a×3×(﹣1)=3,
解得a=﹣1,
∴抛物线解析式为y=﹣(x+3)(x﹣1),
即y=﹣x2﹣2x+3,
设直线BC的解析式为y=mx+n,
把B(﹣3,0),C(0,3)代入得,
解得,
∴直线BC的解析式为y=x+3,
设P(t,t+3)(﹣3<t<0),则M(t,﹣t2﹣2t+3),
∴PM=﹣t2﹣2t+3﹣(t+3)=﹣t2﹣3t,
∵PM=﹣(t+)2+,
∴当t=﹣时,PM有最大值,最大值为.
23.解:(1)y=﹣x2+4x+5=﹣(x﹣2)2+9,
∴M(2,9);
(2)令y=0,得﹣x2+4x+5=0,
解得 x=﹣1或x=5,
∴A(﹣1,0),B(5,0),
令x=0,得y=﹣x2+4x+5=5,
∴C(0,5),
过点M作ME⊥y轴于点E,
∴S△MBC=S四边形MBOE﹣S△MCE﹣S△BOC==15;
(3)存在点N,使得以B,C,N为顶点的三角形是直角三角形,理由如下:
∵OB=OC=5,∠COB=90°,
∴∠OCB=∠OBC=45°,
∴△BOC是等腰直角三角形,
①当C为直角顶点时,作CN1⊥BC交坐标轴为N1,∠CN1B=∠CBN1=45°,
∴OB=ON1=5,
∴N1(﹣5,0);
②当B为直角顶点时,作BN2⊥BC交坐标轴为N2,∠CN2B=∠BCN2=45°,
∴OC=ON2=5,
∴N1(0,﹣5);
③当N为直角顶点时,点O与N3重合,
∴N3(0,0).
综上所述,满足条件的点N的坐标为(﹣5,0)或(0,﹣5)或(0,0).
同课章节目录
