浙教版数学九年级上册第3章圆的基本性质大题练习(含解析)
文档属性
| 名称 | 浙教版数学九年级上册第3章圆的基本性质大题练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 489.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 21:50:10 | ||
图片预览



文档简介
浙教版初中数学九年级上册圆的基本性质-----大题练习
一、解答题
1.如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2 ,BF=2,求阴影部分的面积(结果保留π).
2.在平面直角坐标系中,已知点A(﹣3,1),B(﹣2,0),C(0,1),请在图中画出△ABC,并画出与△ABC关于原点O对称的图形.
3.已知AB为⊙O的直径,弦ED与AB的延长线交于⊙O外一点C,且AB=2CD,∠C=25°,求∠AOE的度数.
4.如图,王虎使一长为4cm,宽为3cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为多少?
5.已知AB为圆O直径,M、N分别为OA、OB中点,CM⊥AB,DN⊥AB。求证:。
6.阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r1,r2,腰上的高为h,连接AP,则S△ABP+S△ACP=S△ABC,即:AB r1+AC r2=AB h,∴r1+r2=h
(1)理解与应用
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:已知边长为2的等边△ABC内任意一点P到各边的距离分别为r1,r2,r3,试证明:r1+r2+r3=.
(2)类比与推理
边长为2的正方形内任意一点到各边的距离的和等于
(3)拓展与延伸
若边长为2的正n边形A1A2…An内部任意一点P到各边的距离为r1,r2,…rn,请问r1+r2+…rn是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值.
7.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
①请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;
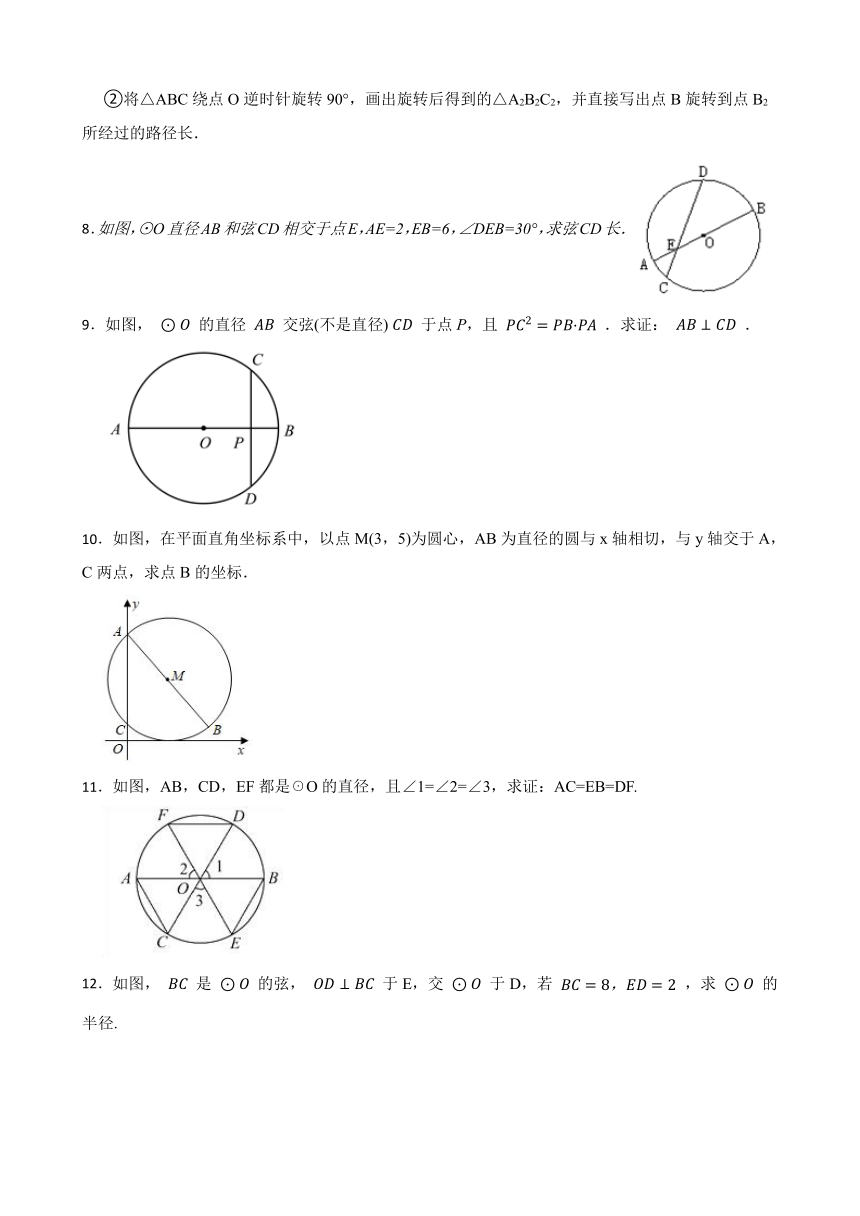
②将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B旋转到点B2所经过的路径长.
8.如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
9.如图, 的直径 交弦(不是直径) 于点P,且 .求证: .
10.如图,在平面直角坐标系中,以点M(3,5)为圆心,AB为直径的圆与x轴相切,与y轴交于A,C两点,求点B的坐标.
11.如图,AB,CD,EF都是☉O的直径,且∠1=∠2=∠3,求证:AC=EB=DF.
12.如图, 是 的弦, 于E,交 于D,若 ,求 的半径.
13.如图,已知A、B、C、D是⊙O上的四点,延长DC、AB相交于点E.若BC=BE.求证:△ADE是等腰三角形.
14.如图,阴影部分是由同心圆的与所围成的.已知OA=3cm,OC=2cm,∠AOB=120o,求阴影部分的面积(结果保留л).
15.在圆O中,直径CD⊥弦AB于E,AB=6, = ,求DE的长.
16.O为等腰△ABC的底边AB的中点,以点O为圆心,AB为直径的半圆分别交AC,BC于点D,E.求证:
(1)∠AOE=∠BOD;
(2)=.
17.如图是庐江中学某景点内的一个拱门,它是⊙O的一部分.已知拱门的地面宽度CD=2m,它的最大高度EM=3m,求构成该拱门的⊙O的半径.
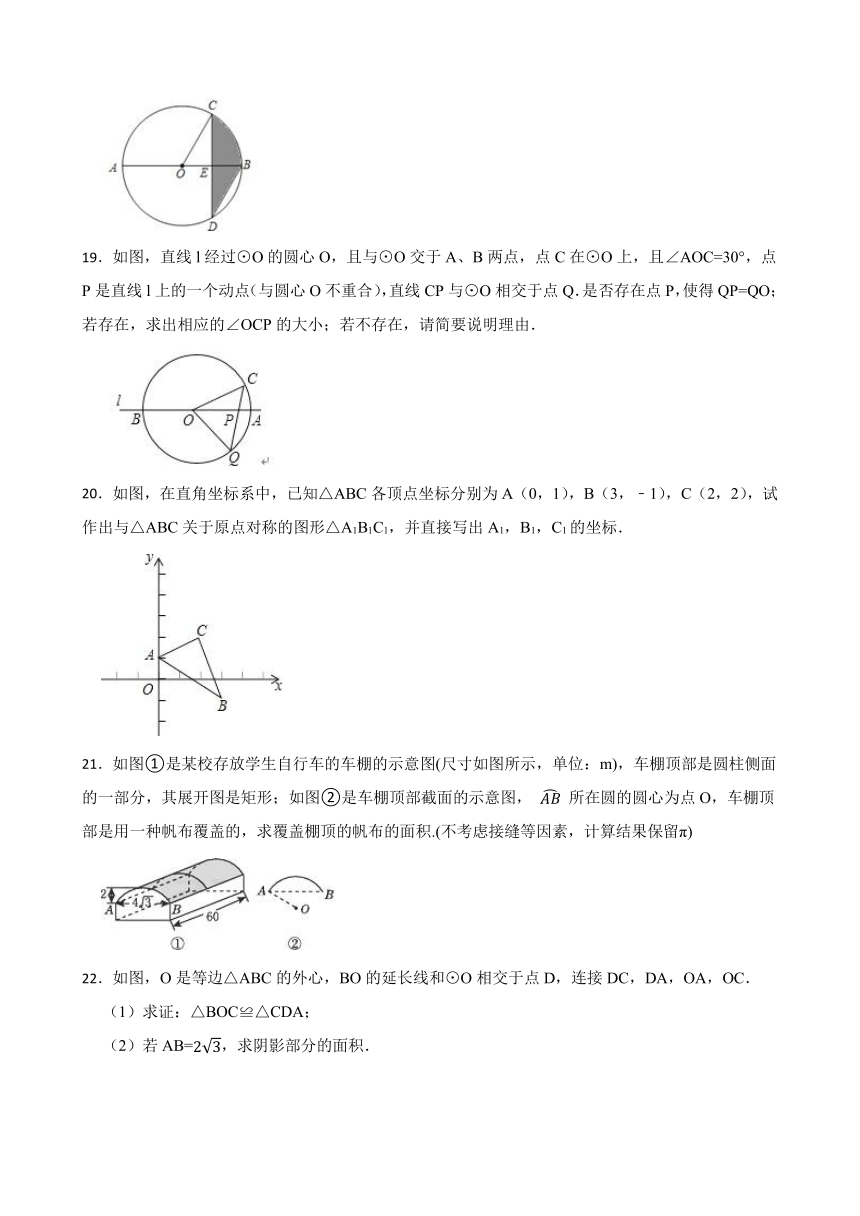
18.)如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,∠CDB=30°,CD=2,求图中阴影部分的面积.
19.如图,直线l经过⊙O的圆心O,且与⊙O交于A、B两点,点C在⊙O上,且∠AOC=30°,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于点Q.是否存在点P,使得QP=QO;若存在,求出相应的∠OCP的大小;若不存在,请简要说明理由.
20.如图,在直角坐标系中,已知△ABC各顶点坐标分别为A(0,1),B(3,﹣1),C(2,2),试作出与△ABC关于原点对称的图形△A1B1C1,并直接写出A1,B1,C1的坐标.
21.如图①是某校存放学生自行车的车棚的示意图(尺寸如图所示,单位:m),车棚顶部是圆柱侧面的一部分,其展开图是矩形;如图②是车棚顶部截面的示意图, 所在圆的圆心为点O,车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积.(不考虑接缝等因素,计算结果保留π)
22.如图,O是等边△ABC的外心,BO的延长线和⊙O相交于点D,连接DC,DA,OA,OC.
(1)求证:△BOC≌△CDA;
(2)若AB=,求阴影部分的面积.
23.如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线交BC于点E.
(1)求证:EB=EC;
(2)当△ABC满足什么条件时,四边形ODEC是正方形?证明你的结论.
24.如图,AB与⊙O相切于点B,BC为⊙O的弦,OC⊥OA,OA与BC相交于点P.
(1)求证:AP=AB;
(2)若OB=4,AB=3,求线段BP的长.
25.如图,已知△ABC内接于⊙O,AD、AE分别平分∠BAC和△BAC的外角∠BAF,且分别交圆于点D、F,连接DE,CD,DE与BC相交于点G.
(1)求证:DE是△ABC的外接圆的直径;
(2)设OG=3,CD=,求⊙O的半径.
答案解析部分
1.【答案】(1)解:BC与⊙O相切.理由如下:
连接OD.
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
又∵OD=OA,
∴∠OAD=∠ODA,
∴∠CAD=∠ODA,
∴OD∥AC,
∴∠ODB=∠C=90°,
即OD⊥BC.
又∵BC过半径OD的外端点D,
∴BC与⊙O相切;
(2)解:设OF=OD=x,则OB=OF+BF=x+2.
根据勾股定理得: ,
即 ,解得:x=2,
即OD=OF=2,
∴OB=2+2=4.
在Rt△ODB中,∵OD= OB,
∴∠B=30°,
∴∠DOB=60°,
∴S扇形DOF= = ,则阴影部分的面积为S△ODB﹣S扇形DOF= = .
故阴影部分的面积为 .
2.【答案】解:作图如下:
3.【答案】解:连结OD,如图,
∵直径AB=2CD,
∴OD=CD,
∴∠DOC=∠C=25°,
∴∠EDO=∠DOC+∠C=50°,
∵OD=OE,
∴∠E=∠EDO=50°,
∴∠AOE=∠E+∠C=75°
4.【答案】解:第一次是以B为旋转中心,BA长5cm为半径旋转90°,
此次点A走过的路径是.
第二次是以C为旋转中心,3cm为半径旋转60°
此次走过的路径是,
∴点A两次共走过的路径是.
5.【答案】解:连结OC、OD,则OC=OD
∵ ,且
在 与 中
∴
6.【答案】(1)解:
分别连接AP,BP,CP,作AD⊥BC于D,
∴∠ADB=90°,
∵△ABC是等边三角形
∴AB=BC=AC=2,∠ABC=60°,
∴∠BAD=30°,
∴BD=1,在Rt△ABD中,由勾股定理,得
∴AD=
∵S△ABP+S△BCP+S△ACP=S△ABC.
∴AB r1+BC r2+AC r3=BC×AD,
∵BC=AC=AB,
∴r1+r2+r3=AD.
∴r1+r2+r3=
(2)4
(3)解:设正n边形的边心距为r,且正n边形的边长为2,∴S正n边形=×2×r×n.r=,∵S正n边形=×2×r1+×2×r2+×2×r1+…+×2×rn,∴×2×r1+×2×r2+×2×r1+…+×2×rn=×n,
∴r1+r2+…+rn=nr=(为定值).
7.【答案】解:如图所示,△A1B1C1、△A2B2C2即为所求;
∵OB= ,∠BOB2=90°,
∴点B旋转到点B2所经过的路径长为 .
8.【答案】解:过O作OF⊥CD,交CD于点F,连接OD,∴F为CD的中点,即CF=DF,∵AE=2,EB=6,∴AB=AE+EB=2+6=8,∴OA=4,∴OE=OA﹣AE=4﹣2=2,在Rt△OEF中,∠DEB=30°,∴OF= OE=1,在Rt△ODF中,OF=1,OD=4,根据勾股定理得:DF= = ,则CD=2DF=2 .
9.【答案】解:连接AC和BD,
在△PAC和△PBD中,
∠A=∠D,∠C=∠B,
∴△PAC∽△PDB,
∴ ,
∴ ,
∵ ,
∴ ,
∴PC=PD,
∵AB为直径,
∴AB⊥CD.
10.【答案】解:如图,连接,
设圆与x轴相切于点D,连接交与点E,则轴,
为直径,则,
,
//轴,
∵M(3,5),
∴MB=MD=5,CE=EB=3,
∴由勾股定理得:ME=4,
∴CB=2CE=6,
∴DE=MD-ME=1
//轴,
∴B(6,1)
11.【答案】解:在☉O中,∵∠1=∠2=∠3,
又∵AB,CD,EF都是☉O的直径,
∴∠FOD=∠AOC=∠BOE.
∴ = = ,
∴AC=EB=DF.
12.【答案】解:连接
设 的半径为R,则
在 中,由勾股定理得
,即
解得
的半径为
13.【答案】解: 四点共圆, 即 是等腰三角形.
14.【答案】解:S阴影=.
15.【答案】解:如图所示,
∵ = ,
∴CE=3DE,
∴CD=CE+DE=4DE,
∴OD= CD=2DE,
∴OE=OD﹣DE=DE,
∴OA=OD=2DE,
∴OA=2OE.
∵CD垂直平分AB,
∴AE= AB= ×6=3,∠AEO=90°,
∴∠OAE=30°,
∴OA= = =2 ,
∴DE= OA= ×2 = .
16.【答案】解:(1)∵CA=CB,
∴∠A=∠B,
∵OA=OD,OB=OE,
∴∠A=∠ODA,∠B=∠OEB,
∴∠AOD=∠BOE,
∴∠AOD+∠DOE=∠BOE+∠DOE,
∴∠AOE=∠BOD;
(2)∵∠AOD=∠BOE,
∴=.
17.【答案】解:连接OC.设⊙O的半径为xm,
∵EM⊥CD,
∴CM=CD=1m.
在Rt△OCM中,由OM2+CM2=OC2,
得(3﹣x)2+1=x2.
解得:x=.
答:构成该拱门的⊙O的半径为m.
18.【答案】解:∵AB是⊙O的直径,弦CD⊥AB,
∴CE=.
∵∠CDB=30°,
∴∠COE=60°,
在Rt△OEC中,OC===2,
∵CE=DE,
∠COE=∠DBE=60°
∴Rt△COE≌Rt△DBE,
∴S阴影=S扇形OBC=π×OC2=π×4=π.
19.【答案】解:①根据题意,画出图(1),
在△QOC中,OC=OQ,
∴∠OQC=∠OCP,
在△OPQ中,QP=QO,
∴∠QOP=∠QPO,
又∵∠AOC=30°,
∴∠QPO=∠OCP+∠AOC=∠OCP+30°,
在△OPQ中,∠QOP+∠QPO+∠OQC=180°,
即(∠OCP+30°)+(∠OCP+30°)+∠OCP=180°,
整理得,3∠OCP=120°,
∴∠OCP=40°.
②当P在线段OA的延长线上(如图2)
∵OC=OQ,
∴∠OQP=(180°﹣∠QOC)×①,
∵OQ=PQ,
∴∠OPQ=(180°﹣∠OQP)×②,
在△OQP中,30°+∠QOC+∠OQP+∠OPQ=180°③,
把①②代入③得∠QOC=20°,则∠OQP=80°
∴∠OCP=100°;
③当P在线段OA的反向延长线上(如图3),
∵OC=OQ,
∴∠OCP=∠OQC=(180°﹣∠COQ)×①,
∵OQ=PQ,
∴∠P=(180°﹣∠OQP)×②,
∵∠AOC=30°,
∴∠COQ+∠POQ=150°③,
∵∠P=∠POQ,2∠P=∠OCP=∠OQC④,
①②③④联立得
∠P=10°,
∴∠OCP=180°﹣150°﹣10°=20°.
故答案为:40°、20°、100°.
20.【答案】解:△A1B1C1如图所示;
A1(0,﹣1),B1(﹣3,1),C1(﹣2,﹣2).
21.【答案】解:如图,连结OB,过点O作OE⊥AB,垂足为E,交 于F,由垂径定理知,E是AB的中点,F是 的中点,从而EF是弓形的高.∵AB=4,∴AE= AB=2 m,EF=2 m.设半径为Rm,则OE=(R-2)m.在Rt△AOE中,∴R2=(R-2)2+(2 )2.∴R=4.在Rt△AEO中,∵AO=2OE,∴∠OAE=30°,∠AOE=60°,∴∠AOB=120°.∴ 的长为=(m).∴覆盖棚顶的帆布的面积为×60=160π(m2).
22.【答案】解:(1)证明:如图1所示:∵O是等边△ABC的外心,∴∠1=∠2,∠3=∠4,∴AD=CD,∵四边形OADC为平行四边形,∴四边形OADC为菱形,∴BD垂直平分AC,∠4=∠5=∠6,而∠1=∠5,∴OA=OC,∠2=∠3,∴OB=OC,∴点O为△ABC的外心,∴△ABC为等边三角形,∴∠AOB=∠BOC=∠AOC=120°,BC=AC,∵四边形OADC为平行四边形,∴∠ADC=∠AOC=120°,AD=OC,CD=OA,∴AD=OB,在△BOC和△CDA中,,∴△BOC≌△CDA(SAS);(2)解:作OH⊥AB于H,如图2所示,∵∠AOB=120°,OA=OB,∴∠BOH=(180°﹣120°)=30°,∵OH⊥AB,∴BH=AH=AB=,OH=BH=1,OB=2OH=2,∴S阴影部分=S扇形AOB﹣S△AOB=﹣××1=π﹣.
23.【答案】(1)证明:连接CD,∵AC是直径,∠ACB=90°,∴BC是⊙O的切线,∠ADC=90°.∵DE是⊙O的切线,
∴DE=CE(切线长定理).
∴∠DCE=∠CDE,又∵∠DCE+∠EBD=∠CDE+∠EDB=90°,∴∠EBD=∠EDB.
∴DE=BE,
∴CE=BE.
(2)解:当△ABC是等腰直角三角形时,四边形ODEC是正方形.证明如下:△ABC是等腰直角三角形.则∠B=45°,
∴∠DCE=∠CDE=45°,则∠DEB=90°,
又∵OC=OD,∠ACB=90°,∴∠OCD=∠ODC=45°,∴∠ODE=90°,
∴四边形ODEC是矩形,
∵EC=ED,∴四边形ODEC是正方形.
24.【答案】(1)证明:∵OC=OB,
∴∠OCB=∠OBC,
∵AB是⊙O的切线,
∴OB⊥AB,
∴∠OBA=90°,
∴∠ABP+∠OBC=90°,
∵OC⊥AO,
∴∠AOC=90°,
∴∠OCB+∠CPO=90°,
∵∠APB=∠CPO,
∴∠APB=∠ABP,
∴AP=AB.
(2)解:作OH⊥BC于H.
在Rt△OAB中,∵OB=4,AB=3,
∴OA= =5,
∵AP=AB=3,
∴PO=2.
在Rt△POC中,PC= =2 ,
PC OH= OC OP,
∴OH= = ,
∴CH= = ,
∵OH⊥BC,
∴CH=BH,
∴BC=2CH= ,
∴PB=BC﹣PC= ﹣2 = .
25.【答案】证明:(1)∵AD、AE分别平分∠BAC和△BAC的外角∠BAF,
∴∠1=∠2,∠3=∠EAF,
∵∠1+∠2+∠3+∠EAF=180°,
∴∠2+∠3=90°,
即∠DAE=90°,
∴DE是△ABC的外接圆的直径;
(2)解:连接OC,如图所示:
设⊙O的半径为r,
则OD=OC=r,DG=r﹣3,
∵∠1=∠2,
∴,
∴OD⊥BC,
∴∠OGC=∠DGC=90°,
由勾股定理得:CG2=CD2﹣DG2,CG2=OC2﹣OG2,
∴CD2﹣DG2=OC2﹣OG2,
即( )2﹣(r﹣3)2=r2﹣32,
解得:r=5,或r=﹣2(不合题意,舍去),
∴⊙O的半径为5.
一、解答题
1.如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2 ,BF=2,求阴影部分的面积(结果保留π).
2.在平面直角坐标系中,已知点A(﹣3,1),B(﹣2,0),C(0,1),请在图中画出△ABC,并画出与△ABC关于原点O对称的图形.
3.已知AB为⊙O的直径,弦ED与AB的延长线交于⊙O外一点C,且AB=2CD,∠C=25°,求∠AOE的度数.
4.如图,王虎使一长为4cm,宽为3cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为多少?
5.已知AB为圆O直径,M、N分别为OA、OB中点,CM⊥AB,DN⊥AB。求证:。
6.阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r1,r2,腰上的高为h,连接AP,则S△ABP+S△ACP=S△ABC,即:AB r1+AC r2=AB h,∴r1+r2=h
(1)理解与应用
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:已知边长为2的等边△ABC内任意一点P到各边的距离分别为r1,r2,r3,试证明:r1+r2+r3=.
(2)类比与推理
边长为2的正方形内任意一点到各边的距离的和等于
(3)拓展与延伸
若边长为2的正n边形A1A2…An内部任意一点P到各边的距离为r1,r2,…rn,请问r1+r2+…rn是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值.
7.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
①请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;
②将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B旋转到点B2所经过的路径长.
8.如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
9.如图, 的直径 交弦(不是直径) 于点P,且 .求证: .
10.如图,在平面直角坐标系中,以点M(3,5)为圆心,AB为直径的圆与x轴相切,与y轴交于A,C两点,求点B的坐标.
11.如图,AB,CD,EF都是☉O的直径,且∠1=∠2=∠3,求证:AC=EB=DF.
12.如图, 是 的弦, 于E,交 于D,若 ,求 的半径.
13.如图,已知A、B、C、D是⊙O上的四点,延长DC、AB相交于点E.若BC=BE.求证:△ADE是等腰三角形.
14.如图,阴影部分是由同心圆的与所围成的.已知OA=3cm,OC=2cm,∠AOB=120o,求阴影部分的面积(结果保留л).
15.在圆O中,直径CD⊥弦AB于E,AB=6, = ,求DE的长.
16.O为等腰△ABC的底边AB的中点,以点O为圆心,AB为直径的半圆分别交AC,BC于点D,E.求证:
(1)∠AOE=∠BOD;
(2)=.
17.如图是庐江中学某景点内的一个拱门,它是⊙O的一部分.已知拱门的地面宽度CD=2m,它的最大高度EM=3m,求构成该拱门的⊙O的半径.
18.)如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,∠CDB=30°,CD=2,求图中阴影部分的面积.
19.如图,直线l经过⊙O的圆心O,且与⊙O交于A、B两点,点C在⊙O上,且∠AOC=30°,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于点Q.是否存在点P,使得QP=QO;若存在,求出相应的∠OCP的大小;若不存在,请简要说明理由.
20.如图,在直角坐标系中,已知△ABC各顶点坐标分别为A(0,1),B(3,﹣1),C(2,2),试作出与△ABC关于原点对称的图形△A1B1C1,并直接写出A1,B1,C1的坐标.
21.如图①是某校存放学生自行车的车棚的示意图(尺寸如图所示,单位:m),车棚顶部是圆柱侧面的一部分,其展开图是矩形;如图②是车棚顶部截面的示意图, 所在圆的圆心为点O,车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积.(不考虑接缝等因素,计算结果保留π)
22.如图,O是等边△ABC的外心,BO的延长线和⊙O相交于点D,连接DC,DA,OA,OC.
(1)求证:△BOC≌△CDA;
(2)若AB=,求阴影部分的面积.
23.如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线交BC于点E.
(1)求证:EB=EC;
(2)当△ABC满足什么条件时,四边形ODEC是正方形?证明你的结论.
24.如图,AB与⊙O相切于点B,BC为⊙O的弦,OC⊥OA,OA与BC相交于点P.
(1)求证:AP=AB;
(2)若OB=4,AB=3,求线段BP的长.
25.如图,已知△ABC内接于⊙O,AD、AE分别平分∠BAC和△BAC的外角∠BAF,且分别交圆于点D、F,连接DE,CD,DE与BC相交于点G.
(1)求证:DE是△ABC的外接圆的直径;
(2)设OG=3,CD=,求⊙O的半径.
答案解析部分
1.【答案】(1)解:BC与⊙O相切.理由如下:
连接OD.
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
又∵OD=OA,
∴∠OAD=∠ODA,
∴∠CAD=∠ODA,
∴OD∥AC,
∴∠ODB=∠C=90°,
即OD⊥BC.
又∵BC过半径OD的外端点D,
∴BC与⊙O相切;
(2)解:设OF=OD=x,则OB=OF+BF=x+2.
根据勾股定理得: ,
即 ,解得:x=2,
即OD=OF=2,
∴OB=2+2=4.
在Rt△ODB中,∵OD= OB,
∴∠B=30°,
∴∠DOB=60°,
∴S扇形DOF= = ,则阴影部分的面积为S△ODB﹣S扇形DOF= = .
故阴影部分的面积为 .
2.【答案】解:作图如下:
3.【答案】解:连结OD,如图,
∵直径AB=2CD,
∴OD=CD,
∴∠DOC=∠C=25°,
∴∠EDO=∠DOC+∠C=50°,
∵OD=OE,
∴∠E=∠EDO=50°,
∴∠AOE=∠E+∠C=75°
4.【答案】解:第一次是以B为旋转中心,BA长5cm为半径旋转90°,
此次点A走过的路径是.
第二次是以C为旋转中心,3cm为半径旋转60°
此次走过的路径是,
∴点A两次共走过的路径是.
5.【答案】解:连结OC、OD,则OC=OD
∵ ,且
在 与 中
∴
6.【答案】(1)解:
分别连接AP,BP,CP,作AD⊥BC于D,
∴∠ADB=90°,
∵△ABC是等边三角形
∴AB=BC=AC=2,∠ABC=60°,
∴∠BAD=30°,
∴BD=1,在Rt△ABD中,由勾股定理,得
∴AD=
∵S△ABP+S△BCP+S△ACP=S△ABC.
∴AB r1+BC r2+AC r3=BC×AD,
∵BC=AC=AB,
∴r1+r2+r3=AD.
∴r1+r2+r3=
(2)4
(3)解:设正n边形的边心距为r,且正n边形的边长为2,∴S正n边形=×2×r×n.r=,∵S正n边形=×2×r1+×2×r2+×2×r1+…+×2×rn,∴×2×r1+×2×r2+×2×r1+…+×2×rn=×n,
∴r1+r2+…+rn=nr=(为定值).
7.【答案】解:如图所示,△A1B1C1、△A2B2C2即为所求;
∵OB= ,∠BOB2=90°,
∴点B旋转到点B2所经过的路径长为 .
8.【答案】解:过O作OF⊥CD,交CD于点F,连接OD,∴F为CD的中点,即CF=DF,∵AE=2,EB=6,∴AB=AE+EB=2+6=8,∴OA=4,∴OE=OA﹣AE=4﹣2=2,在Rt△OEF中,∠DEB=30°,∴OF= OE=1,在Rt△ODF中,OF=1,OD=4,根据勾股定理得:DF= = ,则CD=2DF=2 .
9.【答案】解:连接AC和BD,
在△PAC和△PBD中,
∠A=∠D,∠C=∠B,
∴△PAC∽△PDB,
∴ ,
∴ ,
∵ ,
∴ ,
∴PC=PD,
∵AB为直径,
∴AB⊥CD.
10.【答案】解:如图,连接,
设圆与x轴相切于点D,连接交与点E,则轴,
为直径,则,
,
//轴,
∵M(3,5),
∴MB=MD=5,CE=EB=3,
∴由勾股定理得:ME=4,
∴CB=2CE=6,
∴DE=MD-ME=1
//轴,
∴B(6,1)
11.【答案】解:在☉O中,∵∠1=∠2=∠3,
又∵AB,CD,EF都是☉O的直径,
∴∠FOD=∠AOC=∠BOE.
∴ = = ,
∴AC=EB=DF.
12.【答案】解:连接
设 的半径为R,则
在 中,由勾股定理得
,即
解得
的半径为
13.【答案】解: 四点共圆, 即 是等腰三角形.
14.【答案】解:S阴影=.
15.【答案】解:如图所示,
∵ = ,
∴CE=3DE,
∴CD=CE+DE=4DE,
∴OD= CD=2DE,
∴OE=OD﹣DE=DE,
∴OA=OD=2DE,
∴OA=2OE.
∵CD垂直平分AB,
∴AE= AB= ×6=3,∠AEO=90°,
∴∠OAE=30°,
∴OA= = =2 ,
∴DE= OA= ×2 = .
16.【答案】解:(1)∵CA=CB,
∴∠A=∠B,
∵OA=OD,OB=OE,
∴∠A=∠ODA,∠B=∠OEB,
∴∠AOD=∠BOE,
∴∠AOD+∠DOE=∠BOE+∠DOE,
∴∠AOE=∠BOD;
(2)∵∠AOD=∠BOE,
∴=.
17.【答案】解:连接OC.设⊙O的半径为xm,
∵EM⊥CD,
∴CM=CD=1m.
在Rt△OCM中,由OM2+CM2=OC2,
得(3﹣x)2+1=x2.
解得:x=.
答:构成该拱门的⊙O的半径为m.
18.【答案】解:∵AB是⊙O的直径,弦CD⊥AB,
∴CE=.
∵∠CDB=30°,
∴∠COE=60°,
在Rt△OEC中,OC===2,
∵CE=DE,
∠COE=∠DBE=60°
∴Rt△COE≌Rt△DBE,
∴S阴影=S扇形OBC=π×OC2=π×4=π.
19.【答案】解:①根据题意,画出图(1),
在△QOC中,OC=OQ,
∴∠OQC=∠OCP,
在△OPQ中,QP=QO,
∴∠QOP=∠QPO,
又∵∠AOC=30°,
∴∠QPO=∠OCP+∠AOC=∠OCP+30°,
在△OPQ中,∠QOP+∠QPO+∠OQC=180°,
即(∠OCP+30°)+(∠OCP+30°)+∠OCP=180°,
整理得,3∠OCP=120°,
∴∠OCP=40°.
②当P在线段OA的延长线上(如图2)
∵OC=OQ,
∴∠OQP=(180°﹣∠QOC)×①,
∵OQ=PQ,
∴∠OPQ=(180°﹣∠OQP)×②,
在△OQP中,30°+∠QOC+∠OQP+∠OPQ=180°③,
把①②代入③得∠QOC=20°,则∠OQP=80°
∴∠OCP=100°;
③当P在线段OA的反向延长线上(如图3),
∵OC=OQ,
∴∠OCP=∠OQC=(180°﹣∠COQ)×①,
∵OQ=PQ,
∴∠P=(180°﹣∠OQP)×②,
∵∠AOC=30°,
∴∠COQ+∠POQ=150°③,
∵∠P=∠POQ,2∠P=∠OCP=∠OQC④,
①②③④联立得
∠P=10°,
∴∠OCP=180°﹣150°﹣10°=20°.
故答案为:40°、20°、100°.
20.【答案】解:△A1B1C1如图所示;
A1(0,﹣1),B1(﹣3,1),C1(﹣2,﹣2).
21.【答案】解:如图,连结OB,过点O作OE⊥AB,垂足为E,交 于F,由垂径定理知,E是AB的中点,F是 的中点,从而EF是弓形的高.∵AB=4,∴AE= AB=2 m,EF=2 m.设半径为Rm,则OE=(R-2)m.在Rt△AOE中,∴R2=(R-2)2+(2 )2.∴R=4.在Rt△AEO中,∵AO=2OE,∴∠OAE=30°,∠AOE=60°,∴∠AOB=120°.∴ 的长为=(m).∴覆盖棚顶的帆布的面积为×60=160π(m2).
22.【答案】解:(1)证明:如图1所示:∵O是等边△ABC的外心,∴∠1=∠2,∠3=∠4,∴AD=CD,∵四边形OADC为平行四边形,∴四边形OADC为菱形,∴BD垂直平分AC,∠4=∠5=∠6,而∠1=∠5,∴OA=OC,∠2=∠3,∴OB=OC,∴点O为△ABC的外心,∴△ABC为等边三角形,∴∠AOB=∠BOC=∠AOC=120°,BC=AC,∵四边形OADC为平行四边形,∴∠ADC=∠AOC=120°,AD=OC,CD=OA,∴AD=OB,在△BOC和△CDA中,,∴△BOC≌△CDA(SAS);(2)解:作OH⊥AB于H,如图2所示,∵∠AOB=120°,OA=OB,∴∠BOH=(180°﹣120°)=30°,∵OH⊥AB,∴BH=AH=AB=,OH=BH=1,OB=2OH=2,∴S阴影部分=S扇形AOB﹣S△AOB=﹣××1=π﹣.
23.【答案】(1)证明:连接CD,∵AC是直径,∠ACB=90°,∴BC是⊙O的切线,∠ADC=90°.∵DE是⊙O的切线,
∴DE=CE(切线长定理).
∴∠DCE=∠CDE,又∵∠DCE+∠EBD=∠CDE+∠EDB=90°,∴∠EBD=∠EDB.
∴DE=BE,
∴CE=BE.
(2)解:当△ABC是等腰直角三角形时,四边形ODEC是正方形.证明如下:△ABC是等腰直角三角形.则∠B=45°,
∴∠DCE=∠CDE=45°,则∠DEB=90°,
又∵OC=OD,∠ACB=90°,∴∠OCD=∠ODC=45°,∴∠ODE=90°,
∴四边形ODEC是矩形,
∵EC=ED,∴四边形ODEC是正方形.
24.【答案】(1)证明:∵OC=OB,
∴∠OCB=∠OBC,
∵AB是⊙O的切线,
∴OB⊥AB,
∴∠OBA=90°,
∴∠ABP+∠OBC=90°,
∵OC⊥AO,
∴∠AOC=90°,
∴∠OCB+∠CPO=90°,
∵∠APB=∠CPO,
∴∠APB=∠ABP,
∴AP=AB.
(2)解:作OH⊥BC于H.
在Rt△OAB中,∵OB=4,AB=3,
∴OA= =5,
∵AP=AB=3,
∴PO=2.
在Rt△POC中,PC= =2 ,
PC OH= OC OP,
∴OH= = ,
∴CH= = ,
∵OH⊥BC,
∴CH=BH,
∴BC=2CH= ,
∴PB=BC﹣PC= ﹣2 = .
25.【答案】证明:(1)∵AD、AE分别平分∠BAC和△BAC的外角∠BAF,
∴∠1=∠2,∠3=∠EAF,
∵∠1+∠2+∠3+∠EAF=180°,
∴∠2+∠3=90°,
即∠DAE=90°,
∴DE是△ABC的外接圆的直径;
(2)解:连接OC,如图所示:
设⊙O的半径为r,
则OD=OC=r,DG=r﹣3,
∵∠1=∠2,
∴,
∴OD⊥BC,
∴∠OGC=∠DGC=90°,
由勾股定理得:CG2=CD2﹣DG2,CG2=OC2﹣OG2,
∴CD2﹣DG2=OC2﹣OG2,
即( )2﹣(r﹣3)2=r2﹣32,
解得:r=5,或r=﹣2(不合题意,舍去),
∴⊙O的半径为5.
同课章节目录
