浙教版九年级数学上册第3章圆的基本性质单元达标测试题(含解析)
文档属性
| 名称 | 浙教版九年级数学上册第3章圆的基本性质单元达标测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 655.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 21:47:57 | ||
图片预览



文档简介
2022-2023学年浙教版九年级数学上册《第3章圆的基本性质》单元达标测试题(附答案)
一.选择题(共8小题,满分40分)
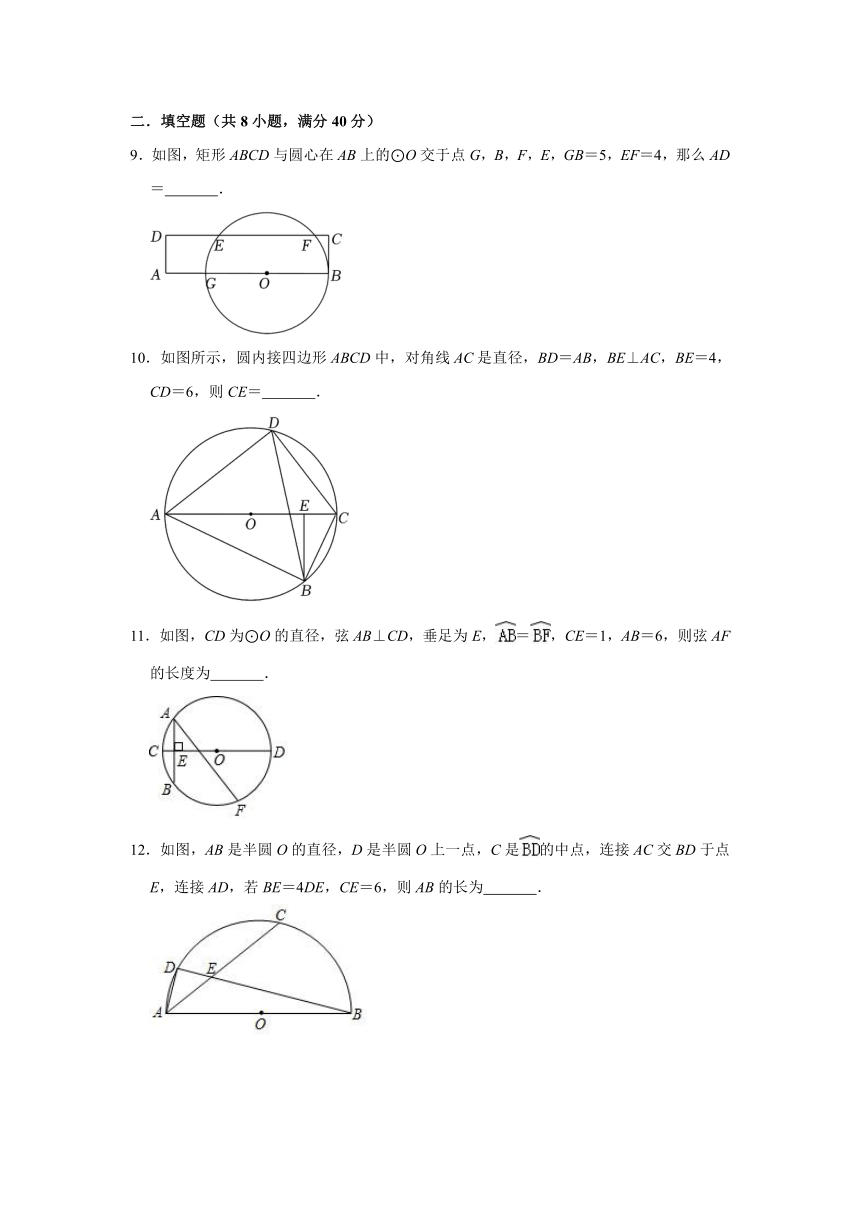
1.如图,四边形ABCD是⊙O的内接四边形,若∠BCD=121°,则∠BOD的度数为( )
A.138° B.121° C.118° D.112°
2.如图,⊙O的直径AB与弦CD相交于点E,若AE=5,EB=1,∠AEC=30°,则CD的长为( )
A.5 B.2 C.4 D.
3.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8,OF=,则OE的长为( )
A.3 B.4 C.2 D.5
4.把半径长为2.5的球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知CD=4,则EF=( )
A.2 B.2.5 C.4 D.5
5.如图,AB是⊙O的直径,弦CD⊥AB于点E,AC=CD,⊙O的半径为2,则△AOC的面积为( )
A. B.2 C.2 D.4
6.如图,AB是⊙O的直径,C是弧AB的中点,点D在弧BC上,AC,BD的延长线交于点E,则∠AEB﹣∠BCD等于( )
A.30° B.45° C.55° D.60°
7.如图,点A的坐标为A(8,0),点B在y轴正半轴上,且AB=10,点P是△AOB外接圆上一点,且∠BOP=45°,则点P的坐标为( )
A.(7,7) B.(7,7) C.(5,5) D.(5,5)
8.如图,四边形ABCD内接于⊙O,AE⊥CB交CB的延长线于点E,若BA平分∠DBE,AD=7,CE=5,则AE=( )
A.3 B. C. D.
二.填空题(共8小题,满分40分)
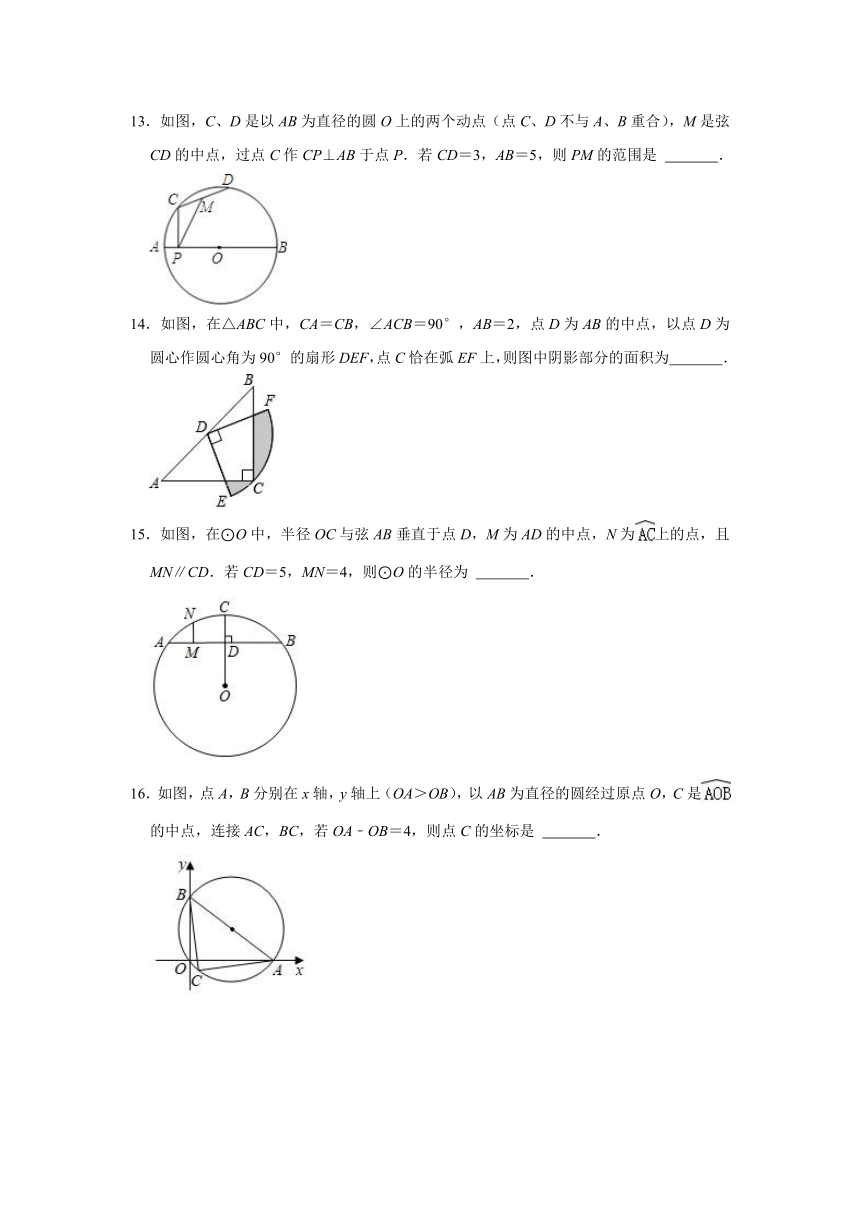
9.如图,矩形ABCD与圆心在AB上的⊙O交于点G,B,F,E,GB=5,EF=4,那么AD= .
10.如图所示,圆内接四边形ABCD中,对角线AC是直径,BD=AB,BE⊥AC,BE=4,CD=6,则CE= .
11.如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,=,CE=1,AB=6,则弦AF的长度为 .
12.如图,AB是半圆O的直径,D是半圆O上一点,C是的中点,连接AC交BD于点E,连接AD,若BE=4DE,CE=6,则AB的长为 .
13.如图,C、D是以AB为直径的圆O上的两个动点(点C、D不与A、B重合),M是弦CD的中点,过点C作CP⊥AB于点P.若CD=3,AB=5,则PM的范围是 .
14.如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为 .
15.如图,在⊙O中,半径OC与弦AB垂直于点D,M为AD的中点,N为上的点,且MN∥CD.若CD=5,MN=4,则⊙O的半径为 .
16.如图,点A,B分别在x轴,y轴上(OA>OB),以AB为直径的圆经过原点O,C是的中点,连接AC,BC,若OA﹣OB=4,则点C的坐标是 .
三.解答题(共5小题,满分40分)
17.如图所示,某地欲搭建一座圆弧型拱桥,跨度AB=32米,拱高CD=8米(C为AB的中点,D为弧AB的中点).
(1)求该圆弧所在圆的半径;
(2)在距离桥的一端4米处欲立一桥墩EF支撑,求桥墩的高度.
18.如图,在Rt△ABC中,∠BAC=90°,以点A为圆心,AC长为半径作圆,交BC于点D,交AB于点E,连接DE.
(1)若∠ABC=20°,求∠DEA的度数;
(2)若AC=3,AB=4,求CD的长.
19.如图,AB是⊙O的直径,C是的中点,CE⊥AB于点E,BD交CE于点F.
(1)求证:CF=BF;
(2)若CD=6,AC=8,求⊙O的半径及CE的长.
20.如图,在⊙O中,AB,AC为弦,CD为直径,AB⊥CD于E,BF⊥AC于F,BF与CD相交于G.
(1)求证:ED=EG;
(2)若AB=8,OG=1,求⊙O的半径.
21.如图,四边形ABCD是⊙O的内接四边形,=,AC为直径,DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)若AC=9,CE=3,求CD的长.
参考答案
一.选择题(共8小题,满分40分)
1.解:∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠BCD=180°,
∴∠A=180°﹣121°=59°,
∴∠BOD=2∠A=2×59°=118°,
故选:C.
2.解:过点O作OF⊥CD于F,连接DO,
∵AE=5,BE=1,
∴AB=6,
∴⊙O的半径为3,
∴OE=3﹣1=2.
∵∠AEC=30°,
∴OF=1,
∴CF=2,
∴CD=2CF=4,
故选:C.
3.解:连接OB、AB,
∵BD⊥AO,BD=8,
∴BE=ED=BD=4,
∵OF⊥BC,
∴CF=FB,
∵CO=OA,OF=,
∴AB=2OF=2,
由勾股定理得:AE==2,
在Rt△BOE中,OB2=OE2+BE2,
即OA2=(OA﹣2)2+42,
解得:OA=5,
∴OE=OA﹣AE=5﹣2=3.
故选:A.
4.解:设球的平面投影圆心为O,过点O作ON⊥AD于点N,延长NO交BC于点M,连接OF,如图所示:
则NF=EN=EF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDNM是矩形,
∴MN=CD=4,ON=MN﹣OM=4﹣2.5=1.5,
在Rt△ONF中,由勾股定理得:ON2+NF2=OF2,
∴NF==2,EF=2NF=4,
故选:C.
5.解:∵CD⊥AB,
∴CE=DE=,∠AEC=90°,
∵AC=CD,
∴CE=,
∴sinA=,
∴∠A=30°,
∵OA=OC,
∴∠A=∠OCA=30°,
∴∠COE=60°,
在Rt△COE中,sin∠COE=,即sin60°=,
∴CE=,
∴S△AOC=
=
=.
故选:C.
6.解:∵AB是⊙O的直径的直径,
∴∠ADB=∠ADE=∠ACB=90°,
∴∠AEB+∠EAD=90°,
∵C是弧AB的中点,
∴AC=BC,
∴∠CAB=∠CBA=45°,
∴∠EAD+∠BAD=45°,
∵∠BCD=∠BAD,
∴∠EAD+∠BCD=45°,
∴∠AEB+∠EAD﹣(∠EAD+∠BCD)=90°﹣45°=45°,
∴∠AEB﹣∠BCD=45°.
故选:B.
7.解:作PH⊥x轴于H,连接PA、PB,
∵∠AOB=90°,
∴AB为△AOB外接圆的直径,
∴∠BPA=90°,
∵AB=10,∠BAP=∠BOP=45°,
∴PA=5,
设OH=t,则PH=t,AH=8﹣t,
在Rt△PHA中,
∵PH2+AH2=PA2,即t2+(8﹣t)2=(5)2,
解得,t1=1(舍去),t2=7,
∴点P的坐标为(7,7),
故选:A.
8.解:连接AC,如图,
∵BA平分∠DBE,
∴∠ABE=∠ABD,
∵∠ABE=∠CDA,∠ABD=∠ACD,
∴∠ACD=∠CDA,
∴AC=AD=7,
∵AE⊥CB,
∴∠AEC=90°,
∴AE===2.
故选:C.
二.填空题(共8小题,满分40分)
9.解:过O作OM⊥EF于M,连接OE,则∠OMD=90°,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴四边形AOMD是矩形,
∴OM=AD,
∵OM⊥EF,OM过圆心O,EF=4,
∴EM=FM=2,
∵OG=OB,BG=5,
∴OB=OG=2.5=OE,
在Rt△OME中,由勾股定理得:OM===1.5,
∴AD=OM=1.5,
故答案为:1.5.
10.解:延长BO交AD于G,连接OD,
∵OA=OD,AB=BD,
∴直线BG是线段AD的垂直平分线,
∴∠AGO=90°,AG=DG,
∵BE⊥AC,
∴∠BEO=∠AGO=90°,
在→AGO和△BEO中,
,
∴△AGO≌△BEO(AAS),
∴AG=BE,
∵BE=4,
∴AG=4,
∴DG=AG=4,
即AD=8,
∵AC是⊙O的直径,
∴∠ABC=∠ADC=90°,
∵CD=6,
∴直径AC==10,
∵∠ABC=∠AEB=∠BEC=90°,
∴∠BAE+∠ABE=90°,∠ABE+∠CBE=90°,
∴∠BAE=∠CBE,
∴=,
解得:CE=2或8,
11解:连接OA、OB,OB交AF于G,如图,
∵AB⊥CD,
∴AE=BE=AB=3,
设⊙O的半径为r,则OE=r﹣1,OA=r,
在Rt△OAE中,32+(r﹣1)2=r2,解得r=5,
∴OE=5﹣1=4,
∵=,
∴OB⊥AF,AG=FG,
∵AG OB=OE AB,
∴AG==,
∴AF=2AG=.
故答案为.
12.解:如图,连接OC交BD于K,连接BC.
∵=,
∴OC⊥BD,
∵BE=4DE,
∴可以假设DE=k.BE=4k,则DK=BK=2.5k,EK=1.5k,
∵AB是直径,
∴∠ADK=∠DKC=∠ACB=90°,
∴AD∥CK,
∴AE:EC=DE:EK,
∴AE:6=k:1.5k,
∴AE=4,
∵△ECK∽△EBC,
∴EC2=EK EB,
∴36=1.5k×4k,
∵k>0,
∴k=,
∴BC===2,
∴AB===4.
故答案为4.
13.解:如图:延长CP交⊙O于N,连接DN.
∵AB⊥CN,
∴CP=PN,
∵CM=DM,
∴PM=DN,
∴当DN为直径时,PM的值最大,最大值为,
当DN=NC时,PM最小,最小值为0,
∴PM的范围是0≤PM≤且PM≠1.5.
故答案为:0≤PM≤且PM≠1.5.
14.解:连接CD,
∵CA=CB,∠ACB=90°,
∴∠B=45°,
∵点D为AB的中点,
∴DC=AB=BD=1,CD⊥AB,∠DCA=45°,
∴∠CDH=∠BDG,∠DCH=∠B,
在△DCH和△DBG中,
,
∴△DCH≌△DBG(ASA),
∴S四边形DGCH=S△BDC=S△ABC=AB CD=×2×1=.
∴S阴影=S扇形DEF﹣S△BDC=﹣=﹣.
故答案为﹣.
15.解:连接AO,ON,延长NM交⊙O于F,过O作OE⊥NF于E,如图,设⊙O的半径为r,AD=t,
∵CD⊥AB,MN∥CD,
∴∠ODM=∠DME=∠MEO=90°,
∴四边形MEOD是矩形,
∴OE=DM=t,OD=ME=r﹣5,
在Rt△AOD中,(r﹣5)2+t2=r2,①
在Rt△NOE中,(r﹣5+4)2+(t)2=r2,②
②×4﹣①得2r﹣21=0,
解得r=,
即⊙O的半径为.
故答案为:.
16.解:∵C是的中点,
∴=,
∴AC=BC,
过点C作CD⊥OA,CE⊥OB,
∴∠BEC=∠ADC=90°
在△BCE和△ACD中,
,
∴△BCE≌△ACD(AAS),
∴AD=BE,CE=CD,
∵∠DOE=∠OEC=∠ODC=90°,
∴四边形ODCE是矩形,
∵CE=CD,
∴矩形ODCE是正方形,
∴OD=OD=CD=CE,
∵AD=OA﹣OD,BE=OB+BE=OB+OD,
∵AD=BE,
∴OA﹣OD=OB+OD,
∵OA﹣OB=4,
∴OD=2,
∴CD=CE=2,
∴C(2,﹣2).
故答案为:(2,﹣2).
三.解答题(共5小题,满分40分)
17.解:(1)设弧AB所在的圆心为O,D为弧AB的中点,CD⊥AB于C,延长DC经过O点,设⊙O的半径为R,
在Rt△OBC中,OB2=OC2+CB2,
∴R2=(R﹣8)2+162,
解得R=20;
(2)OH⊥FE于H,则OH=CE=16﹣4=12,OF′=R=20,
在Rt△OHF中,HF==16,
∵HE=OC=OD﹣CD=20﹣8=12,EF=HF﹣HE=16﹣12=4(米),
∴在离桥的一端4米处,桥墩高4米.
18.解:(1)如图,连接AD.
∵∠BAC=90°,∠ABC=20°,
∴∠ACD=70°.
∵AC=AD,
∴∠ACD=∠ADC=70°,
∴∠CAD=180°﹣70°﹣70°=40°,
∴∠DAE=90°﹣40°=50°.
又∵AD=AE,
∴.
(2)如图,过点A作AF⊥CD,垂足为F.
∵∠BAC=90°,AC=3,AB=4,
∴BC=5.
又∵ AF BC= AC AB,
∴,
∴.
∵AC=AD,AF⊥CD,
∴.
19.(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A=90°﹣∠ABC.
∵CE⊥AB,
∴∠CEB=90°,
∴∠ECB=90°﹣∠ABC,
∴∠ECB=∠A.
又∵C是的中点,
∴=,
∴∠DBC=∠A,
∴∠ECB=∠DBC,
∴CF=BF;
(2)解:∵=,
∴BC=CD=6,
∵∠ACB=90°,
∴AB===10,
∴⊙O的半径为5,
∵S△ABC=AB CE=BC AC,
∴CE===.
20.(1)证明:如图:连接BD,
∵AB⊥CD于E,BF⊥AC于F,
∴∠CFG=∠GEB,
∵∠CGF=∠BGE,
∴∠C=∠GBE,
∵∠C=∠DBE,
∴∠GBE=∠DBE,
∵AB⊥CD于E,
∴∠GEB=∠DEB,
在△GBE和△DBE中,
,
∴△BGE≌△BDE(ASA),
∴ED=EG.
(2)解:如图:
连接OA,设OA=r,则DG=r+1,
由(1)可知ED=EG,
∴OE=,
∵AB⊥CD于E,AB=8,
∴AE=BE=4,
∴在Rt△OAE中,根据勾股定理得:OE2+AE2=OA2,
即()2+42=r2,
解得:r=,
即⊙O的半径为.
21.(1)证明:∵四边形ABCD是⊙O内接四边形,
∴∠BAD+∠BCD=180°,
∵∠BCD+∠DCE=180°,
∴∠DCE=∠BAD,
∵=,
∴∠BAD=∠ACD,
∴∠DCE=∠ACD,
∴CD平分∠ACE;
(2)解:∵AC为直径,
∴∠ADC=90°,
∵DE⊥BC,
∴∠DEC=90°,
∴∠DEC=∠ADC,
∵∠DCE=∠ACD,
∴=,即=,
∴CD=3.
一.选择题(共8小题,满分40分)
1.如图,四边形ABCD是⊙O的内接四边形,若∠BCD=121°,则∠BOD的度数为( )
A.138° B.121° C.118° D.112°
2.如图,⊙O的直径AB与弦CD相交于点E,若AE=5,EB=1,∠AEC=30°,则CD的长为( )
A.5 B.2 C.4 D.
3.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8,OF=,则OE的长为( )
A.3 B.4 C.2 D.5
4.把半径长为2.5的球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知CD=4,则EF=( )
A.2 B.2.5 C.4 D.5
5.如图,AB是⊙O的直径,弦CD⊥AB于点E,AC=CD,⊙O的半径为2,则△AOC的面积为( )
A. B.2 C.2 D.4
6.如图,AB是⊙O的直径,C是弧AB的中点,点D在弧BC上,AC,BD的延长线交于点E,则∠AEB﹣∠BCD等于( )
A.30° B.45° C.55° D.60°
7.如图,点A的坐标为A(8,0),点B在y轴正半轴上,且AB=10,点P是△AOB外接圆上一点,且∠BOP=45°,则点P的坐标为( )
A.(7,7) B.(7,7) C.(5,5) D.(5,5)
8.如图,四边形ABCD内接于⊙O,AE⊥CB交CB的延长线于点E,若BA平分∠DBE,AD=7,CE=5,则AE=( )
A.3 B. C. D.
二.填空题(共8小题,满分40分)
9.如图,矩形ABCD与圆心在AB上的⊙O交于点G,B,F,E,GB=5,EF=4,那么AD= .
10.如图所示,圆内接四边形ABCD中,对角线AC是直径,BD=AB,BE⊥AC,BE=4,CD=6,则CE= .
11.如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,=,CE=1,AB=6,则弦AF的长度为 .
12.如图,AB是半圆O的直径,D是半圆O上一点,C是的中点,连接AC交BD于点E,连接AD,若BE=4DE,CE=6,则AB的长为 .
13.如图,C、D是以AB为直径的圆O上的两个动点(点C、D不与A、B重合),M是弦CD的中点,过点C作CP⊥AB于点P.若CD=3,AB=5,则PM的范围是 .
14.如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为 .
15.如图,在⊙O中,半径OC与弦AB垂直于点D,M为AD的中点,N为上的点,且MN∥CD.若CD=5,MN=4,则⊙O的半径为 .
16.如图,点A,B分别在x轴,y轴上(OA>OB),以AB为直径的圆经过原点O,C是的中点,连接AC,BC,若OA﹣OB=4,则点C的坐标是 .
三.解答题(共5小题,满分40分)
17.如图所示,某地欲搭建一座圆弧型拱桥,跨度AB=32米,拱高CD=8米(C为AB的中点,D为弧AB的中点).
(1)求该圆弧所在圆的半径;
(2)在距离桥的一端4米处欲立一桥墩EF支撑,求桥墩的高度.
18.如图,在Rt△ABC中,∠BAC=90°,以点A为圆心,AC长为半径作圆,交BC于点D,交AB于点E,连接DE.
(1)若∠ABC=20°,求∠DEA的度数;
(2)若AC=3,AB=4,求CD的长.
19.如图,AB是⊙O的直径,C是的中点,CE⊥AB于点E,BD交CE于点F.
(1)求证:CF=BF;
(2)若CD=6,AC=8,求⊙O的半径及CE的长.
20.如图,在⊙O中,AB,AC为弦,CD为直径,AB⊥CD于E,BF⊥AC于F,BF与CD相交于G.
(1)求证:ED=EG;
(2)若AB=8,OG=1,求⊙O的半径.
21.如图,四边形ABCD是⊙O的内接四边形,=,AC为直径,DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)若AC=9,CE=3,求CD的长.
参考答案
一.选择题(共8小题,满分40分)
1.解:∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠BCD=180°,
∴∠A=180°﹣121°=59°,
∴∠BOD=2∠A=2×59°=118°,
故选:C.
2.解:过点O作OF⊥CD于F,连接DO,
∵AE=5,BE=1,
∴AB=6,
∴⊙O的半径为3,
∴OE=3﹣1=2.
∵∠AEC=30°,
∴OF=1,
∴CF=2,
∴CD=2CF=4,
故选:C.
3.解:连接OB、AB,
∵BD⊥AO,BD=8,
∴BE=ED=BD=4,
∵OF⊥BC,
∴CF=FB,
∵CO=OA,OF=,
∴AB=2OF=2,
由勾股定理得:AE==2,
在Rt△BOE中,OB2=OE2+BE2,
即OA2=(OA﹣2)2+42,
解得:OA=5,
∴OE=OA﹣AE=5﹣2=3.
故选:A.
4.解:设球的平面投影圆心为O,过点O作ON⊥AD于点N,延长NO交BC于点M,连接OF,如图所示:
则NF=EN=EF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDNM是矩形,
∴MN=CD=4,ON=MN﹣OM=4﹣2.5=1.5,
在Rt△ONF中,由勾股定理得:ON2+NF2=OF2,
∴NF==2,EF=2NF=4,
故选:C.
5.解:∵CD⊥AB,
∴CE=DE=,∠AEC=90°,
∵AC=CD,
∴CE=,
∴sinA=,
∴∠A=30°,
∵OA=OC,
∴∠A=∠OCA=30°,
∴∠COE=60°,
在Rt△COE中,sin∠COE=,即sin60°=,
∴CE=,
∴S△AOC=
=
=.
故选:C.
6.解:∵AB是⊙O的直径的直径,
∴∠ADB=∠ADE=∠ACB=90°,
∴∠AEB+∠EAD=90°,
∵C是弧AB的中点,
∴AC=BC,
∴∠CAB=∠CBA=45°,
∴∠EAD+∠BAD=45°,
∵∠BCD=∠BAD,
∴∠EAD+∠BCD=45°,
∴∠AEB+∠EAD﹣(∠EAD+∠BCD)=90°﹣45°=45°,
∴∠AEB﹣∠BCD=45°.
故选:B.
7.解:作PH⊥x轴于H,连接PA、PB,
∵∠AOB=90°,
∴AB为△AOB外接圆的直径,
∴∠BPA=90°,
∵AB=10,∠BAP=∠BOP=45°,
∴PA=5,
设OH=t,则PH=t,AH=8﹣t,
在Rt△PHA中,
∵PH2+AH2=PA2,即t2+(8﹣t)2=(5)2,
解得,t1=1(舍去),t2=7,
∴点P的坐标为(7,7),
故选:A.
8.解:连接AC,如图,
∵BA平分∠DBE,
∴∠ABE=∠ABD,
∵∠ABE=∠CDA,∠ABD=∠ACD,
∴∠ACD=∠CDA,
∴AC=AD=7,
∵AE⊥CB,
∴∠AEC=90°,
∴AE===2.
故选:C.
二.填空题(共8小题,满分40分)
9.解:过O作OM⊥EF于M,连接OE,则∠OMD=90°,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴四边形AOMD是矩形,
∴OM=AD,
∵OM⊥EF,OM过圆心O,EF=4,
∴EM=FM=2,
∵OG=OB,BG=5,
∴OB=OG=2.5=OE,
在Rt△OME中,由勾股定理得:OM===1.5,
∴AD=OM=1.5,
故答案为:1.5.
10.解:延长BO交AD于G,连接OD,
∵OA=OD,AB=BD,
∴直线BG是线段AD的垂直平分线,
∴∠AGO=90°,AG=DG,
∵BE⊥AC,
∴∠BEO=∠AGO=90°,
在→AGO和△BEO中,
,
∴△AGO≌△BEO(AAS),
∴AG=BE,
∵BE=4,
∴AG=4,
∴DG=AG=4,
即AD=8,
∵AC是⊙O的直径,
∴∠ABC=∠ADC=90°,
∵CD=6,
∴直径AC==10,
∵∠ABC=∠AEB=∠BEC=90°,
∴∠BAE+∠ABE=90°,∠ABE+∠CBE=90°,
∴∠BAE=∠CBE,
∴=,
解得:CE=2或8,
11解:连接OA、OB,OB交AF于G,如图,
∵AB⊥CD,
∴AE=BE=AB=3,
设⊙O的半径为r,则OE=r﹣1,OA=r,
在Rt△OAE中,32+(r﹣1)2=r2,解得r=5,
∴OE=5﹣1=4,
∵=,
∴OB⊥AF,AG=FG,
∵AG OB=OE AB,
∴AG==,
∴AF=2AG=.
故答案为.
12.解:如图,连接OC交BD于K,连接BC.
∵=,
∴OC⊥BD,
∵BE=4DE,
∴可以假设DE=k.BE=4k,则DK=BK=2.5k,EK=1.5k,
∵AB是直径,
∴∠ADK=∠DKC=∠ACB=90°,
∴AD∥CK,
∴AE:EC=DE:EK,
∴AE:6=k:1.5k,
∴AE=4,
∵△ECK∽△EBC,
∴EC2=EK EB,
∴36=1.5k×4k,
∵k>0,
∴k=,
∴BC===2,
∴AB===4.
故答案为4.
13.解:如图:延长CP交⊙O于N,连接DN.
∵AB⊥CN,
∴CP=PN,
∵CM=DM,
∴PM=DN,
∴当DN为直径时,PM的值最大,最大值为,
当DN=NC时,PM最小,最小值为0,
∴PM的范围是0≤PM≤且PM≠1.5.
故答案为:0≤PM≤且PM≠1.5.
14.解:连接CD,
∵CA=CB,∠ACB=90°,
∴∠B=45°,
∵点D为AB的中点,
∴DC=AB=BD=1,CD⊥AB,∠DCA=45°,
∴∠CDH=∠BDG,∠DCH=∠B,
在△DCH和△DBG中,
,
∴△DCH≌△DBG(ASA),
∴S四边形DGCH=S△BDC=S△ABC=AB CD=×2×1=.
∴S阴影=S扇形DEF﹣S△BDC=﹣=﹣.
故答案为﹣.
15.解:连接AO,ON,延长NM交⊙O于F,过O作OE⊥NF于E,如图,设⊙O的半径为r,AD=t,
∵CD⊥AB,MN∥CD,
∴∠ODM=∠DME=∠MEO=90°,
∴四边形MEOD是矩形,
∴OE=DM=t,OD=ME=r﹣5,
在Rt△AOD中,(r﹣5)2+t2=r2,①
在Rt△NOE中,(r﹣5+4)2+(t)2=r2,②
②×4﹣①得2r﹣21=0,
解得r=,
即⊙O的半径为.
故答案为:.
16.解:∵C是的中点,
∴=,
∴AC=BC,
过点C作CD⊥OA,CE⊥OB,
∴∠BEC=∠ADC=90°
在△BCE和△ACD中,
,
∴△BCE≌△ACD(AAS),
∴AD=BE,CE=CD,
∵∠DOE=∠OEC=∠ODC=90°,
∴四边形ODCE是矩形,
∵CE=CD,
∴矩形ODCE是正方形,
∴OD=OD=CD=CE,
∵AD=OA﹣OD,BE=OB+BE=OB+OD,
∵AD=BE,
∴OA﹣OD=OB+OD,
∵OA﹣OB=4,
∴OD=2,
∴CD=CE=2,
∴C(2,﹣2).
故答案为:(2,﹣2).
三.解答题(共5小题,满分40分)
17.解:(1)设弧AB所在的圆心为O,D为弧AB的中点,CD⊥AB于C,延长DC经过O点,设⊙O的半径为R,
在Rt△OBC中,OB2=OC2+CB2,
∴R2=(R﹣8)2+162,
解得R=20;
(2)OH⊥FE于H,则OH=CE=16﹣4=12,OF′=R=20,
在Rt△OHF中,HF==16,
∵HE=OC=OD﹣CD=20﹣8=12,EF=HF﹣HE=16﹣12=4(米),
∴在离桥的一端4米处,桥墩高4米.
18.解:(1)如图,连接AD.
∵∠BAC=90°,∠ABC=20°,
∴∠ACD=70°.
∵AC=AD,
∴∠ACD=∠ADC=70°,
∴∠CAD=180°﹣70°﹣70°=40°,
∴∠DAE=90°﹣40°=50°.
又∵AD=AE,
∴.
(2)如图,过点A作AF⊥CD,垂足为F.
∵∠BAC=90°,AC=3,AB=4,
∴BC=5.
又∵ AF BC= AC AB,
∴,
∴.
∵AC=AD,AF⊥CD,
∴.
19.(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A=90°﹣∠ABC.
∵CE⊥AB,
∴∠CEB=90°,
∴∠ECB=90°﹣∠ABC,
∴∠ECB=∠A.
又∵C是的中点,
∴=,
∴∠DBC=∠A,
∴∠ECB=∠DBC,
∴CF=BF;
(2)解:∵=,
∴BC=CD=6,
∵∠ACB=90°,
∴AB===10,
∴⊙O的半径为5,
∵S△ABC=AB CE=BC AC,
∴CE===.
20.(1)证明:如图:连接BD,
∵AB⊥CD于E,BF⊥AC于F,
∴∠CFG=∠GEB,
∵∠CGF=∠BGE,
∴∠C=∠GBE,
∵∠C=∠DBE,
∴∠GBE=∠DBE,
∵AB⊥CD于E,
∴∠GEB=∠DEB,
在△GBE和△DBE中,
,
∴△BGE≌△BDE(ASA),
∴ED=EG.
(2)解:如图:
连接OA,设OA=r,则DG=r+1,
由(1)可知ED=EG,
∴OE=,
∵AB⊥CD于E,AB=8,
∴AE=BE=4,
∴在Rt△OAE中,根据勾股定理得:OE2+AE2=OA2,
即()2+42=r2,
解得:r=,
即⊙O的半径为.
21.(1)证明:∵四边形ABCD是⊙O内接四边形,
∴∠BAD+∠BCD=180°,
∵∠BCD+∠DCE=180°,
∴∠DCE=∠BAD,
∵=,
∴∠BAD=∠ACD,
∴∠DCE=∠ACD,
∴CD平分∠ACE;
(2)解:∵AC为直径,
∴∠ADC=90°,
∵DE⊥BC,
∴∠DEC=90°,
∴∠DEC=∠ADC,
∵∠DCE=∠ACD,
∴=,即=,
∴CD=3.
同课章节目录
