2022—2023学年浙教版数学八年级上册1.6尺规作图 课后练习 (含答案)
文档属性
| 名称 | 2022—2023学年浙教版数学八年级上册1.6尺规作图 课后练习 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 648.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 00:00:00 | ||
图片预览


文档简介
浙教版初中数学八年级上册1.6尺规作图-------课后练习
一、单选题
1.过点向边作垂线段,下列画法中正确的是( )
A. B.
C. D.
2.已知点P在 ABC的边BC上,且满足PA=PC,则下列确定点P位置的尺规作图,正确的是( )
A. B.
C. D.
3.如图,在 中, , ,观察图中尺规作图的痕迹,可知 的度数为( )
A.40° B.50° C.55° D.60°
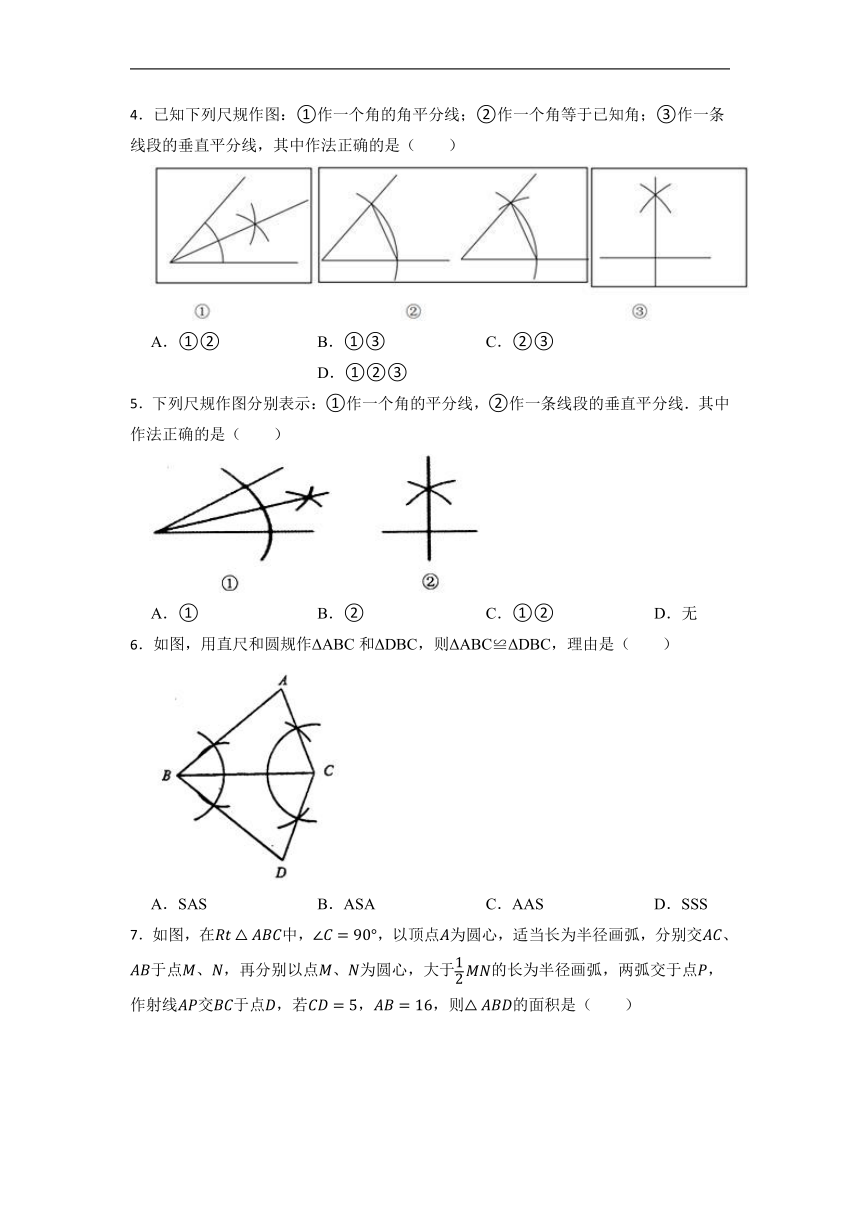
4.已知下列尺规作图:①作一个角的角平分线;②作一个角等于已知角;③作一条线段的垂直平分线,其中作法正确的是( )
A.①② B.①③ C.②③ D.①②③
5.下列尺规作图分别表示:①作一个角的平分线,②作一条线段的垂直平分线.其中作法正确的是( )
A.① B.② C.①② D.无
6.如图,用直尺和圆规作ΔABC和ΔDBC,则ΔABC≌ΔDBC,理由是( )
A.SAS B.ASA C.AAS D.SSS
7.如图,在中,,以顶点为圆心,适当长为半径画弧,分别交、于点、,再分别以点、为圆心,大于的长为半径画弧,两弧交于点,作射线交于点,若,,则的面积是( )
A.21 B.80 C.40 D.45
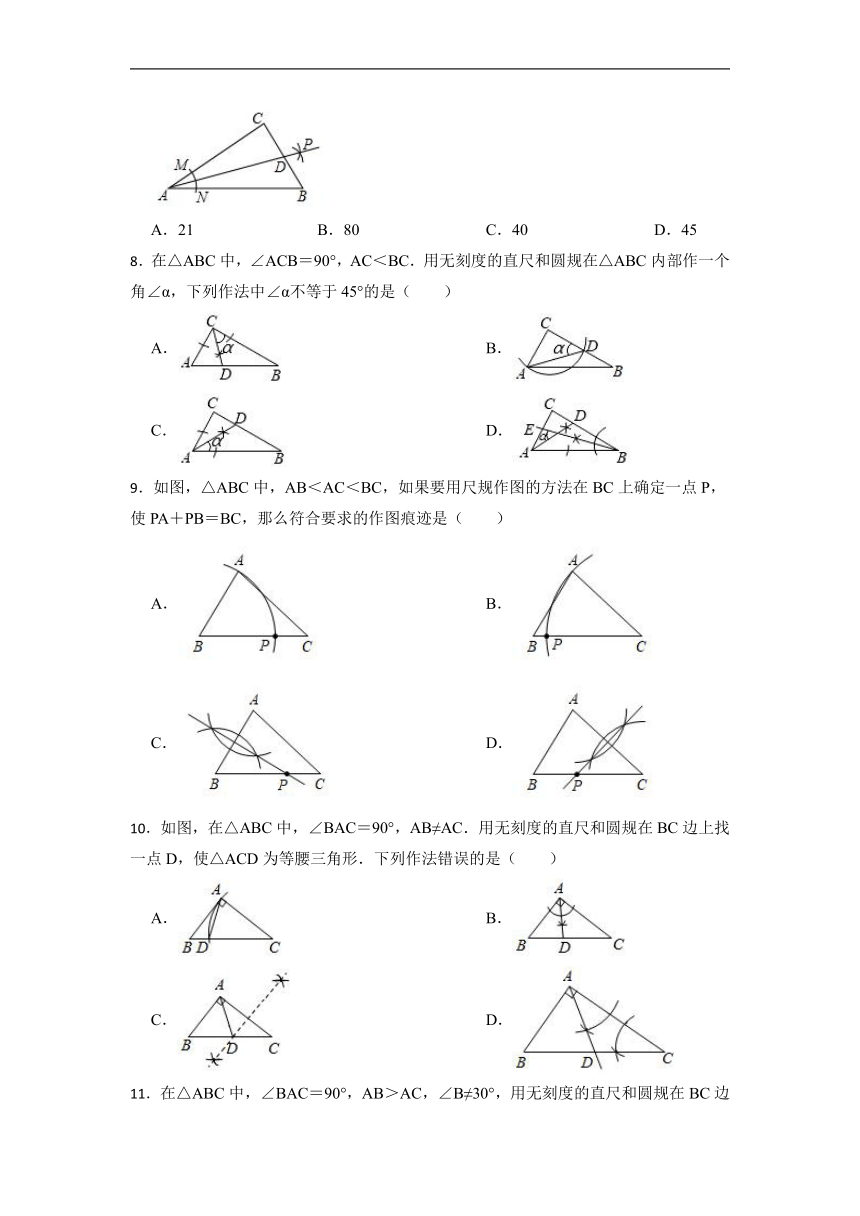
8.在△ABC中,∠ACB=90°,AC<BC.用无刻度的直尺和圆规在△ABC内部作一个角∠α,下列作法中∠α不等于45°的是( )
A. B.
C. D.
9.如图,△ABC中,AB<AC<BC,如果要用尺规作图的方法在BC上确定一点P,使PA+PB=BC,那么符合要求的作图痕迹是( )
A. B.
C. D.
10.如图,在△ABC中,∠BAC=90°,AB≠AC.用无刻度的直尺和圆规在BC边上找一点D,使△ACD为等腰三角形.下列作法错误的是( )
A. B.
C. D.
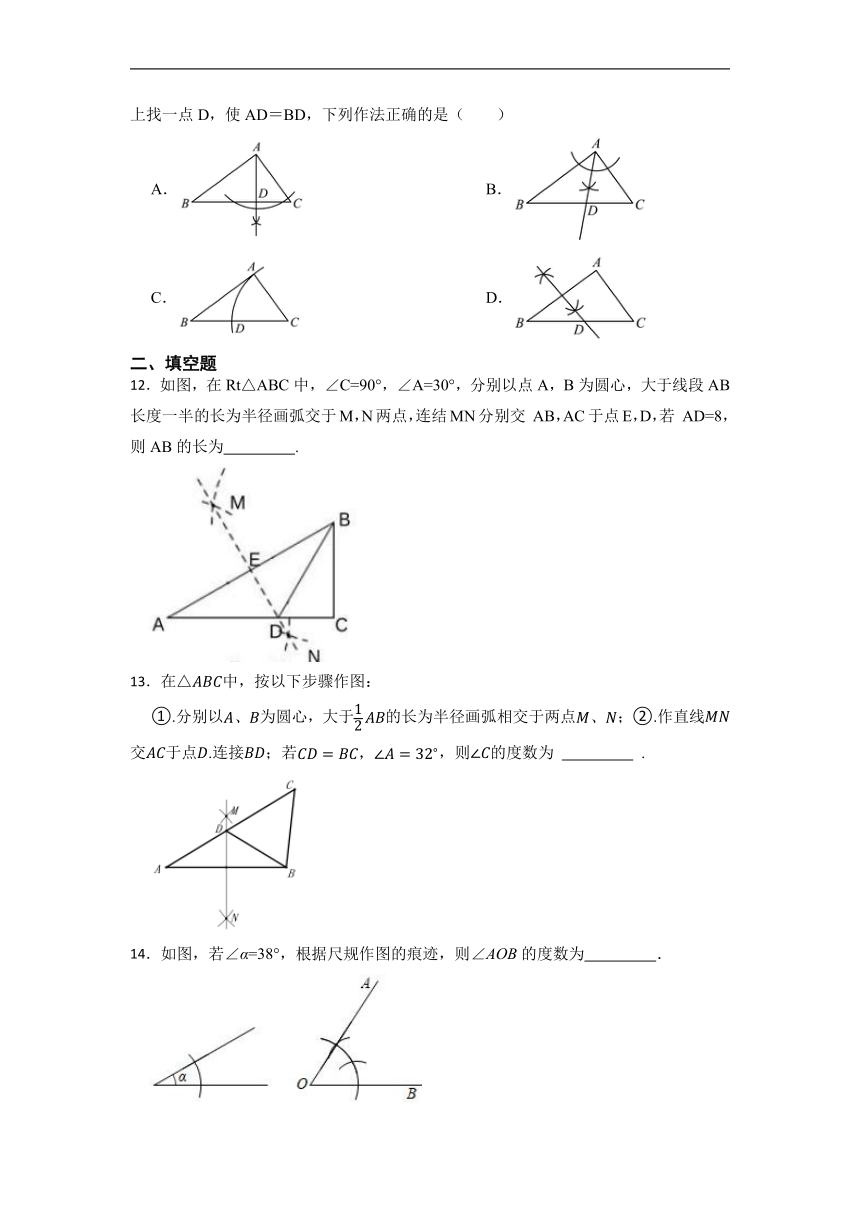
11.在△ABC中,∠BAC=90°,AB>AC,∠B≠30°,用无刻度的直尺和圆规在BC边上找一点D,使AD=BD,下列作法正确的是( )
A. B.
C. D.
二、填空题
12.如图,在Rt△ABC中,∠C=90°,∠A=30°,分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧交于M,N两点,连结MN分别交 AB,AC于点E,D,若 AD=8,则AB的长为 .
13.在△中,按以下步骤作图:
①.分别以为圆心,大于的长为半径画弧相交于两点;②.作直线交于点.连接;若,则的度数为 .
14.如图,若∠α=38°,根据尺规作图的痕迹,则∠AOB的度数为 .
15.如图,在 中, , ,以 为圆心,任意长为半径画弧分别交 、 于点 和 ,再分别以 、 为圆心,大于 的长为半径画弧,两弧交于点 ,连结 并延长交 于点 ,则下列说法① 是 的平分线;② ;③点 在 的中垂线上;正确的个数是 个.
三、作图题
16.如图,已知线段 ,用两种不同的方法作一点 ,使得 .
要求:(1)尺规作图;
(2)保留作图的痕迹,写出必要的文字说明.
17.如图,在 ABC中,∠C=90°,按下列要求用直尺和圆规作图.(不写作法,保留作图痕迹)
(1)如图①,在边BC上求作一点P,使点P到点C的距离等于点P到边AB的距离;
(2)如图②,在边AB上求作一点Q,使点Q到点A的距离等于点Q到边BC的距离.
18.如图,ABCD,CD交BF于E.
(1)尺规作图:以点D为顶点,射线DC为一边,在DC的右侧作∠CDG,使∠CDG=∠B.(要求:不写作法,但保留作图痕迹)
(2)证明:DGBF.
19.如图,在9×4的方格纸ABCD中,每个小正方形的边长均为1,点E为格点(注:小正方形顶点称为格点).请仅用无刻度直尺按要求画图.
⑴在CD边上找一点P,连结AP,使△AEP是等腰三角形;
⑵在AB边上找一点Q,使EQ⊥AP,画出线段EQ.
20.如图,在4x4的方格纸中,请按要求画格点三角形(顶点在格点上).
(1)在图1中画格点△PQO,使△PQO是以点P为直角顶点的等腰直角三角形.
(2)在图2中画格点△QMN,使PQ是△QMN 的中线,且M,N不在同一条网格线上.
21.如图,△ABC的顶点A、B、C都在小正方形的顶点上,利用网格线按下列要求画图.
( 1 )画△A1B1C1,使它与△ABC关于直线l成轴对称;
( 2 )在直线l上找一点P,使点P到点A、B的距离之和最短;
( 3 )在直线l上找一点Q,使点Q到边AC、BC所在直线的距离相等.
四、综合题
22.已知中,.
(1)如图1,用直尺和圆规在的内部作射线,使,我们可以通过以下步骤作图:
①以点为圆心,适当长为半径作弧,分别交,分别于点,;
②以为圆心,的长为半径作弧,交于点;
③以点为圆心,长为半径作弧,交上一段弧于点.
④做射线;
请回答:这种作“”的方法的依据是 填序号.
(2)如图2,当时,(1)中的射线交于点,已知,,,求的长.
23.如图,已知ABC.
(1)请用直尺和圆规作∠ABC的角平分线BD,交AC于点D.(保留作图痕迹,不写作法)
(2)在(1)的条件下,若,,求∠BDA的度数.
24.下面是小军设计的“过线段端点作这条线段的垂线”的尺规作图过程.
已知:线段AB.
求作:AB的垂线,使它经过点A.
作法:如图,
①以点A为圆心,AB长为半径作弧,交线段BA的延长线于点C;
②分别以点B和点C为圆心,大于BC的长为半径作弧,两弧相交于直线BC上方的点D;
③作直线AD.
所以直线AD就是所求作的垂线.
根据小军设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接CD,BD.
∵BD= ▲ ,AB= ▲ ,
∴AD⊥AB( ▲ )(填推理的依据).
25.已知:如图1,线段a,b().
(1)求作:等腰ABC,使得它的底边长为b,底边上的高的长为a.
作法:①作线段.
②作线段AB的垂直平分线MN,与AB相交于点D.
③在MN上取一点C,使.
④连接AC,BC,则ABC就是所求作的等腰三角形.
用直尺和圆规在图2中补全图形(要求:保留作图痕迹);
(2)求作:等腰PEF,使得它的腰长为线段a,b中一条线段的长,底边上的高的长为线段a,b中另一条线段的长.
作法:①作直线l,在直线l上取一点G.
②过点G作直线l的垂线GH.
③在GH上取一点P,使PG= ▲ .
④以P为圆心,以 ▲ 的长为半径画弧,与直线l分别相交于点E,F.
⑤连接PE,PF,则PEF就是所求作的等腰三角形.
请补全作法,并用直尺和圆规在图3中补全图形(要求:保留作图痕迹).
26.下面是小东设计的尺规作图过程.
已知:如图,在Rt中,°.
求作:点,使得点在边上,且到和的距离相等.
作法:①如图,以点为圆心,任意长为半径画弧,分别交,于点,;
②分别以点,为圆心,大于为半径画弧,两弧交于点;
③画射线,交于点.
所以点即为所求.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:过点作于点,连接.
在和中,
∵,,,
∴≌(SSS).
∴∠ ▲ =∠ ▲ .
∵∠=90°,
∴.
∵,
∴( ▲ ).
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】B
4.【答案】A
5.【答案】A
6.【答案】B
7.【答案】C
8.【答案】C
9.【答案】D
10.【答案】B
11.【答案】D
12.【答案】
13.【答案】52°
14.【答案】76
15.【答案】3
16.【答案】解:作法一如下,
说明:作AB的垂直平分线EF,与AB交于N,作NC=NB,可得CN=AN=NB,∠ANC=∠BNC=90°,从而△ANC和△BNC为等腰直角三角形,∠CAN=∠BCN=45°,所以可得∠ACB=90°;
作法二如下,
说明:过点A向右上方作射线AM,过点B作AM的垂线与AM交于C,连接BC,则∠ACB=90°.
17.【答案】(1)解:如图①,点P即为所求作;
(2)解:如图②,点Q即为所求作.
18.【答案】(1)解:如图所示, 即为所求;
(2)证明:∵
∴∠B=∠CEF
∵∠B=∠D
∴∠CEF=∠D
∴ //
19.【答案】解:(1)如图,△AEP即为所求;
(2)如图,线段EQ即为所求.
20.【答案】(1)解:如图,
(2)解:
如图,
21.【答案】⑴解:如图,分别作出A,B,C的对应点A1,B1,C1,△A1B1C1即为所求作.
⑵解:如图连接A1B交直线l于点P,点P即为所求作,点P即为所求作.
⑶解:如图∠ACB的角平分线与直线l的交点Q即为所求作,点Q即为所求作.
22.【答案】(1)①
(2)解:如图2中,取 的中点 ,连接 .
, , ,
,
,
,
是等边三角形,
, ,
,
,
,
.
23.【答案】(1)解:如图
(2)解:∵∠A=100°,∠C=28°,
∴,
又∵BD平分∠ABC,
∴∠DBC=26°,
∴.
24.【答案】(1)解:补全的图形如图所示:
(2)证明:连接CD,BD.
∵BD=CD,AB=AC ,
∴AD⊥AB(等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合)(填推理的依据).
故答案为:CD,AC,等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合
25.【答案】(1)解:如图,ABC就是所求作的等腰三角形;
(2)解:作法:①作直线l,在直线l上取一点G.
②过点G作直线l的垂线GH.
③在GH上取一点P,使PG=a.
④以P为圆心,以b的长为半径画弧,与直线l分别相交于点E,F.
⑤连接PE,PF,则PEF就是所求作的等腰三角形.
如图,PEF就是所求作的等腰三角形.
故答案为:a,b.
26.【答案】(1)解:补全的图形如下:
(2)解:过点作于点,连接.
在和中,
∵,,,
∴≌(SSS).
∴∠PAM=∠PAN.
∴=90°,
∴.
∵,
∴(角的平分线上的点到角的两边的距离相等).
故答案为:∠,∠,角的平分线上的点到角的两边的距离相等
一、单选题
1.过点向边作垂线段,下列画法中正确的是( )
A. B.
C. D.
2.已知点P在 ABC的边BC上,且满足PA=PC,则下列确定点P位置的尺规作图,正确的是( )
A. B.
C. D.
3.如图,在 中, , ,观察图中尺规作图的痕迹,可知 的度数为( )
A.40° B.50° C.55° D.60°
4.已知下列尺规作图:①作一个角的角平分线;②作一个角等于已知角;③作一条线段的垂直平分线,其中作法正确的是( )
A.①② B.①③ C.②③ D.①②③
5.下列尺规作图分别表示:①作一个角的平分线,②作一条线段的垂直平分线.其中作法正确的是( )
A.① B.② C.①② D.无
6.如图,用直尺和圆规作ΔABC和ΔDBC,则ΔABC≌ΔDBC,理由是( )
A.SAS B.ASA C.AAS D.SSS
7.如图,在中,,以顶点为圆心,适当长为半径画弧,分别交、于点、,再分别以点、为圆心,大于的长为半径画弧,两弧交于点,作射线交于点,若,,则的面积是( )
A.21 B.80 C.40 D.45
8.在△ABC中,∠ACB=90°,AC<BC.用无刻度的直尺和圆规在△ABC内部作一个角∠α,下列作法中∠α不等于45°的是( )
A. B.
C. D.
9.如图,△ABC中,AB<AC<BC,如果要用尺规作图的方法在BC上确定一点P,使PA+PB=BC,那么符合要求的作图痕迹是( )
A. B.
C. D.
10.如图,在△ABC中,∠BAC=90°,AB≠AC.用无刻度的直尺和圆规在BC边上找一点D,使△ACD为等腰三角形.下列作法错误的是( )
A. B.
C. D.
11.在△ABC中,∠BAC=90°,AB>AC,∠B≠30°,用无刻度的直尺和圆规在BC边上找一点D,使AD=BD,下列作法正确的是( )
A. B.
C. D.
二、填空题
12.如图,在Rt△ABC中,∠C=90°,∠A=30°,分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧交于M,N两点,连结MN分别交 AB,AC于点E,D,若 AD=8,则AB的长为 .
13.在△中,按以下步骤作图:
①.分别以为圆心,大于的长为半径画弧相交于两点;②.作直线交于点.连接;若,则的度数为 .
14.如图,若∠α=38°,根据尺规作图的痕迹,则∠AOB的度数为 .
15.如图,在 中, , ,以 为圆心,任意长为半径画弧分别交 、 于点 和 ,再分别以 、 为圆心,大于 的长为半径画弧,两弧交于点 ,连结 并延长交 于点 ,则下列说法① 是 的平分线;② ;③点 在 的中垂线上;正确的个数是 个.
三、作图题
16.如图,已知线段 ,用两种不同的方法作一点 ,使得 .
要求:(1)尺规作图;
(2)保留作图的痕迹,写出必要的文字说明.
17.如图,在 ABC中,∠C=90°,按下列要求用直尺和圆规作图.(不写作法,保留作图痕迹)
(1)如图①,在边BC上求作一点P,使点P到点C的距离等于点P到边AB的距离;
(2)如图②,在边AB上求作一点Q,使点Q到点A的距离等于点Q到边BC的距离.
18.如图,ABCD,CD交BF于E.
(1)尺规作图:以点D为顶点,射线DC为一边,在DC的右侧作∠CDG,使∠CDG=∠B.(要求:不写作法,但保留作图痕迹)
(2)证明:DGBF.
19.如图,在9×4的方格纸ABCD中,每个小正方形的边长均为1,点E为格点(注:小正方形顶点称为格点).请仅用无刻度直尺按要求画图.
⑴在CD边上找一点P,连结AP,使△AEP是等腰三角形;
⑵在AB边上找一点Q,使EQ⊥AP,画出线段EQ.
20.如图,在4x4的方格纸中,请按要求画格点三角形(顶点在格点上).
(1)在图1中画格点△PQO,使△PQO是以点P为直角顶点的等腰直角三角形.
(2)在图2中画格点△QMN,使PQ是△QMN 的中线,且M,N不在同一条网格线上.
21.如图,△ABC的顶点A、B、C都在小正方形的顶点上,利用网格线按下列要求画图.
( 1 )画△A1B1C1,使它与△ABC关于直线l成轴对称;
( 2 )在直线l上找一点P,使点P到点A、B的距离之和最短;
( 3 )在直线l上找一点Q,使点Q到边AC、BC所在直线的距离相等.
四、综合题
22.已知中,.
(1)如图1,用直尺和圆规在的内部作射线,使,我们可以通过以下步骤作图:
①以点为圆心,适当长为半径作弧,分别交,分别于点,;
②以为圆心,的长为半径作弧,交于点;
③以点为圆心,长为半径作弧,交上一段弧于点.
④做射线;
请回答:这种作“”的方法的依据是 填序号.
(2)如图2,当时,(1)中的射线交于点,已知,,,求的长.
23.如图,已知ABC.
(1)请用直尺和圆规作∠ABC的角平分线BD,交AC于点D.(保留作图痕迹,不写作法)
(2)在(1)的条件下,若,,求∠BDA的度数.
24.下面是小军设计的“过线段端点作这条线段的垂线”的尺规作图过程.
已知:线段AB.
求作:AB的垂线,使它经过点A.
作法:如图,
①以点A为圆心,AB长为半径作弧,交线段BA的延长线于点C;
②分别以点B和点C为圆心,大于BC的长为半径作弧,两弧相交于直线BC上方的点D;
③作直线AD.
所以直线AD就是所求作的垂线.
根据小军设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接CD,BD.
∵BD= ▲ ,AB= ▲ ,
∴AD⊥AB( ▲ )(填推理的依据).
25.已知:如图1,线段a,b().
(1)求作:等腰ABC,使得它的底边长为b,底边上的高的长为a.
作法:①作线段.
②作线段AB的垂直平分线MN,与AB相交于点D.
③在MN上取一点C,使.
④连接AC,BC,则ABC就是所求作的等腰三角形.
用直尺和圆规在图2中补全图形(要求:保留作图痕迹);
(2)求作:等腰PEF,使得它的腰长为线段a,b中一条线段的长,底边上的高的长为线段a,b中另一条线段的长.
作法:①作直线l,在直线l上取一点G.
②过点G作直线l的垂线GH.
③在GH上取一点P,使PG= ▲ .
④以P为圆心,以 ▲ 的长为半径画弧,与直线l分别相交于点E,F.
⑤连接PE,PF,则PEF就是所求作的等腰三角形.
请补全作法,并用直尺和圆规在图3中补全图形(要求:保留作图痕迹).
26.下面是小东设计的尺规作图过程.
已知:如图,在Rt中,°.
求作:点,使得点在边上,且到和的距离相等.
作法:①如图,以点为圆心,任意长为半径画弧,分别交,于点,;
②分别以点,为圆心,大于为半径画弧,两弧交于点;
③画射线,交于点.
所以点即为所求.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:过点作于点,连接.
在和中,
∵,,,
∴≌(SSS).
∴∠ ▲ =∠ ▲ .
∵∠=90°,
∴.
∵,
∴( ▲ ).
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】B
4.【答案】A
5.【答案】A
6.【答案】B
7.【答案】C
8.【答案】C
9.【答案】D
10.【答案】B
11.【答案】D
12.【答案】
13.【答案】52°
14.【答案】76
15.【答案】3
16.【答案】解:作法一如下,
说明:作AB的垂直平分线EF,与AB交于N,作NC=NB,可得CN=AN=NB,∠ANC=∠BNC=90°,从而△ANC和△BNC为等腰直角三角形,∠CAN=∠BCN=45°,所以可得∠ACB=90°;
作法二如下,
说明:过点A向右上方作射线AM,过点B作AM的垂线与AM交于C,连接BC,则∠ACB=90°.
17.【答案】(1)解:如图①,点P即为所求作;
(2)解:如图②,点Q即为所求作.
18.【答案】(1)解:如图所示, 即为所求;
(2)证明:∵
∴∠B=∠CEF
∵∠B=∠D
∴∠CEF=∠D
∴ //
19.【答案】解:(1)如图,△AEP即为所求;
(2)如图,线段EQ即为所求.
20.【答案】(1)解:如图,
(2)解:
如图,
21.【答案】⑴解:如图,分别作出A,B,C的对应点A1,B1,C1,△A1B1C1即为所求作.
⑵解:如图连接A1B交直线l于点P,点P即为所求作,点P即为所求作.
⑶解:如图∠ACB的角平分线与直线l的交点Q即为所求作,点Q即为所求作.
22.【答案】(1)①
(2)解:如图2中,取 的中点 ,连接 .
, , ,
,
,
,
是等边三角形,
, ,
,
,
,
.
23.【答案】(1)解:如图
(2)解:∵∠A=100°,∠C=28°,
∴,
又∵BD平分∠ABC,
∴∠DBC=26°,
∴.
24.【答案】(1)解:补全的图形如图所示:
(2)证明:连接CD,BD.
∵BD=CD,AB=AC ,
∴AD⊥AB(等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合)(填推理的依据).
故答案为:CD,AC,等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合
25.【答案】(1)解:如图,ABC就是所求作的等腰三角形;
(2)解:作法:①作直线l,在直线l上取一点G.
②过点G作直线l的垂线GH.
③在GH上取一点P,使PG=a.
④以P为圆心,以b的长为半径画弧,与直线l分别相交于点E,F.
⑤连接PE,PF,则PEF就是所求作的等腰三角形.
如图,PEF就是所求作的等腰三角形.
故答案为:a,b.
26.【答案】(1)解:补全的图形如下:
(2)解:过点作于点,连接.
在和中,
∵,,,
∴≌(SSS).
∴∠PAM=∠PAN.
∴=90°,
∴.
∵,
∴(角的平分线上的点到角的两边的距离相等).
故答案为:∠,∠,角的平分线上的点到角的两边的距离相等
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
