浙教版数学八年级上册2.1 图形的轴对称 课时练习(含答案)
文档属性
| 名称 | 浙教版数学八年级上册2.1 图形的轴对称 课时练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 219.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 00:00:00 | ||
图片预览


文档简介
2022-2023年浙教版数学八年级上册2.1
《图形的轴对称》课时练习
一 、选择题
下列图形中,右边图形与左边图形成轴对称的是( )
下列说法中,正确的是( )
A.关于某条直线对称的两个三角形是全等三角形
B.全等的两个三角形是关于某条直线对称的
C.两个图形关于某条直线对称,则这两个图形一定分别位于这条直线的两侧
D.全等的两个图形一定成轴对称
如图,关于虚线成轴对称的有( )个.
A.1 B.2 C.3 D.4
对于下列命题:
(1)关于某一直线成轴对称的两个三角形全等;
(2)等腰三角形的对称轴是顶角的平分线;
(3)一条线段的两个端点一定是关于经过该线段中点的直线的对称点;
(4)如果两个三角形全等,那么它们关于某直线成轴对称.
其中真命题的个数为 ( )
A.0 B.1 C.2 D.3
选择观察下列平面图形,其中是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
一名同学想用正方形和圆设计一个图案,要求整个图案关于正方形的某条对角线对称,
那么下列图案中不符合要求的是( )
已知点A,B是两个居民区的位置,现在准备在墙l边上建立一个垃圾站点P,如图是4位设计师给出的规划图,其中PA+PB距离最短的是( )
如图,直线l外不重合的两点A,B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:
①作点B关于直线l的对称点B/
②连接AB/,与直线l相交于点C,则点C为所求作的点.
在解决这个问题时没有运用到的知识或方法是( )
A.转化思想
B.三角形的两边之和大于第三边
C.两点之间,线段最短
D.三角形的一个外角大于与它不相邻的任意一个内角
到三角形三个顶点的距离都相等的点是这个三角形的( )
A.三条高的交点 B.三条角平分线的交点
C.三条中线的交点 D.三条边的垂直平分线的交点
如图,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( )
A.1对 B.2对 C.3对 D.4对
二 、填空题
如图,图形是由棋子围成的正方形图案,图案的每条边有4个棋子,这个图案有_____条对称轴.
从平面镜子中看到镜子对面电子钟示数的像如图所示,这时的时刻应是 .
如图,台球桌相邻两边互相垂直,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么打白球时,必须保证∠1的度数为 °.
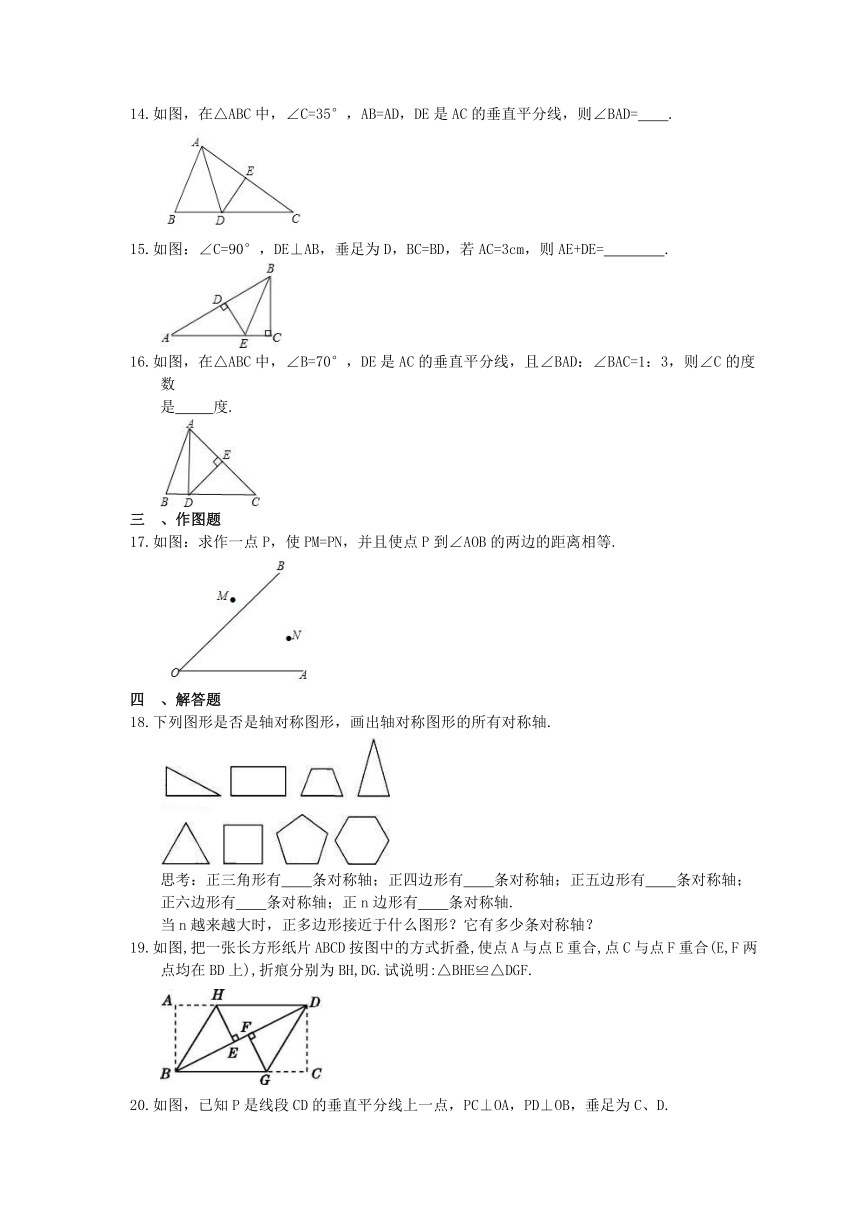
如图,在△ABC中,∠C=35°,AB=AD,DE是AC的垂直平分线,则∠BAD= .
如图:∠C=90°,DE⊥AB,垂足为D,BC=BD,若AC=3cm,则AE+DE= .
如图,在△ABC中,∠B=70°,DE是AC的垂直平分线,且∠BAD:∠BAC=1:3,则∠C的度数
是 度.
三 、作图题
如图:求作一点P,使PM=PN,并且使点P到∠AOB的两边的距离相等.
四 、解答题
下列图形是否是轴对称图形,画出轴对称图形的所有对称轴.
思考:正三角形有 条对称轴;正四边形有 条对称轴;正五边形有 条对称轴;正六边形有 条对称轴;正n边形有 条对称轴.
当n越来越大时,正多边形接近于什么图形?它有多少条对称轴?
如图,把一张长方形纸片ABCD按图中的方式折叠,使点A与点E重合,点C与点F重合(E,F两点均在BD上),折痕分别为BH,DG.试说明:△BHE≌△DGF.
如图,已知P是线段CD的垂直平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
求证:(1)OC=OD;(2)OP平分∠AOB.
在△ABC中,AB>BC,AB=AC,DE是AB的垂直平分线,垂足为D点,交AC于点E.
(1)若∠ABE=38°,求∠EBC的度数;
(2)若△ABC的周长为36cm,一边为13cm,求△BCE的周长.
如图,已知△ABC,∠C=Rt∠,AC<BC,D为BC上一点,且到A,B两点的距离相等.
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=37°,求∠CAD的度数.
如图,在△ABC中,BE是角平分线,AD⊥BE,垂足为D.
求证:∠2=∠1+∠C.
2022-2023年浙教版数学八年级上册2.1《图形的轴对称》课时练习(含答案)参考答案
一 、选择题
答案为:B
答案为:A
答案为:B
答案为:C
答案为:C
答案为:D
答案为:D.
答案为:D.
D
答案为:D.
二 、填空题
答案为:4
答案为:21:05
答案是:60.
答案为:40°.
答案为:3cm;
答案为:44°.
三 、作图题
解:如图,点P即为所求.
(1)作∠AOB 的平分线OC;
(2)连结MN,并作MN 的垂直平分线EF,交OC于P,连结PM、PN,
则P点即为所求.
四 、解答题
解:正三角形有3条对称轴;正四边形有4条对称轴;正五边形有5条对称轴;
正六边形有6条对称轴;正n边形有n条对称轴.
当n越来越大时,正多边形接近于圆形,它有无数条对称轴.
故答案为:3,4,5,6,n.
作图如下:
解:由折叠可知:
∠ABH=∠EBH=∠ABD,∠CDG=∠GDF=∠CDB,
∠HEB=∠A=∠GFD=∠C=90°,
AB=BE,CD=FD.
因为AB∥CD,
所以∠ABD=∠CDB.
所以∠EBH=∠GDF.
因为AB=CD,
所以BE=DF.
所以△BHE≌△DGF.
证明:(1)∵P在CD的垂直平分线上,
∴PC=PD.
又∵OP=OP,
∴Rt△OPC≌Rt△OPD(HL).
∴OC=OD.
(2)由(1)Rt△OPC≌△OPD知∠AOP=∠BOP.
解:(1)∵DE是AB的垂直平分线,
∴AE=BE,
∴∠A=∠ABE=38°
∵AB=AC,
∴∠ABC=∠C=71°
∴∠EBC=∠ABC-∠ABE=71°-38°=33°
(2)由△ABC的周长为36cm
AB>BC,AB=AC
可知AB=AC=13cm BC=10cm
△BCE的周长=BE+CE+BC=AC+BC=13+10=23(cm)
解:(1)如图,点D为所作;
(2)∵DA=DB,
∴∠DAB=∠B=37°,
∵∠BAC=∠C﹣∠B=90°﹣37°=53°,
∴∠CAD=53°﹣37°=16°.
证明:如图,延长AD交BC于点F,
∵BE是角平分线,AD⊥BE,
∴△ABF是等腰三角形,且∠2=∠AFB,
又∵∠AFB=∠1+∠C,
∴∠2=∠1+∠C.
《图形的轴对称》课时练习
一 、选择题
下列图形中,右边图形与左边图形成轴对称的是( )
下列说法中,正确的是( )
A.关于某条直线对称的两个三角形是全等三角形
B.全等的两个三角形是关于某条直线对称的
C.两个图形关于某条直线对称,则这两个图形一定分别位于这条直线的两侧
D.全等的两个图形一定成轴对称
如图,关于虚线成轴对称的有( )个.
A.1 B.2 C.3 D.4
对于下列命题:
(1)关于某一直线成轴对称的两个三角形全等;
(2)等腰三角形的对称轴是顶角的平分线;
(3)一条线段的两个端点一定是关于经过该线段中点的直线的对称点;
(4)如果两个三角形全等,那么它们关于某直线成轴对称.
其中真命题的个数为 ( )
A.0 B.1 C.2 D.3
选择观察下列平面图形,其中是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
一名同学想用正方形和圆设计一个图案,要求整个图案关于正方形的某条对角线对称,
那么下列图案中不符合要求的是( )
已知点A,B是两个居民区的位置,现在准备在墙l边上建立一个垃圾站点P,如图是4位设计师给出的规划图,其中PA+PB距离最短的是( )
如图,直线l外不重合的两点A,B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:
①作点B关于直线l的对称点B/
②连接AB/,与直线l相交于点C,则点C为所求作的点.
在解决这个问题时没有运用到的知识或方法是( )
A.转化思想
B.三角形的两边之和大于第三边
C.两点之间,线段最短
D.三角形的一个外角大于与它不相邻的任意一个内角
到三角形三个顶点的距离都相等的点是这个三角形的( )
A.三条高的交点 B.三条角平分线的交点
C.三条中线的交点 D.三条边的垂直平分线的交点
如图,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( )
A.1对 B.2对 C.3对 D.4对
二 、填空题
如图,图形是由棋子围成的正方形图案,图案的每条边有4个棋子,这个图案有_____条对称轴.
从平面镜子中看到镜子对面电子钟示数的像如图所示,这时的时刻应是 .
如图,台球桌相邻两边互相垂直,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么打白球时,必须保证∠1的度数为 °.
如图,在△ABC中,∠C=35°,AB=AD,DE是AC的垂直平分线,则∠BAD= .
如图:∠C=90°,DE⊥AB,垂足为D,BC=BD,若AC=3cm,则AE+DE= .
如图,在△ABC中,∠B=70°,DE是AC的垂直平分线,且∠BAD:∠BAC=1:3,则∠C的度数
是 度.
三 、作图题
如图:求作一点P,使PM=PN,并且使点P到∠AOB的两边的距离相等.
四 、解答题
下列图形是否是轴对称图形,画出轴对称图形的所有对称轴.
思考:正三角形有 条对称轴;正四边形有 条对称轴;正五边形有 条对称轴;正六边形有 条对称轴;正n边形有 条对称轴.
当n越来越大时,正多边形接近于什么图形?它有多少条对称轴?
如图,把一张长方形纸片ABCD按图中的方式折叠,使点A与点E重合,点C与点F重合(E,F两点均在BD上),折痕分别为BH,DG.试说明:△BHE≌△DGF.
如图,已知P是线段CD的垂直平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
求证:(1)OC=OD;(2)OP平分∠AOB.
在△ABC中,AB>BC,AB=AC,DE是AB的垂直平分线,垂足为D点,交AC于点E.
(1)若∠ABE=38°,求∠EBC的度数;
(2)若△ABC的周长为36cm,一边为13cm,求△BCE的周长.
如图,已知△ABC,∠C=Rt∠,AC<BC,D为BC上一点,且到A,B两点的距离相等.
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=37°,求∠CAD的度数.
如图,在△ABC中,BE是角平分线,AD⊥BE,垂足为D.
求证:∠2=∠1+∠C.
2022-2023年浙教版数学八年级上册2.1《图形的轴对称》课时练习(含答案)参考答案
一 、选择题
答案为:B
答案为:A
答案为:B
答案为:C
答案为:C
答案为:D
答案为:D.
答案为:D.
D
答案为:D.
二 、填空题
答案为:4
答案为:21:05
答案是:60.
答案为:40°.
答案为:3cm;
答案为:44°.
三 、作图题
解:如图,点P即为所求.
(1)作∠AOB 的平分线OC;
(2)连结MN,并作MN 的垂直平分线EF,交OC于P,连结PM、PN,
则P点即为所求.
四 、解答题
解:正三角形有3条对称轴;正四边形有4条对称轴;正五边形有5条对称轴;
正六边形有6条对称轴;正n边形有n条对称轴.
当n越来越大时,正多边形接近于圆形,它有无数条对称轴.
故答案为:3,4,5,6,n.
作图如下:
解:由折叠可知:
∠ABH=∠EBH=∠ABD,∠CDG=∠GDF=∠CDB,
∠HEB=∠A=∠GFD=∠C=90°,
AB=BE,CD=FD.
因为AB∥CD,
所以∠ABD=∠CDB.
所以∠EBH=∠GDF.
因为AB=CD,
所以BE=DF.
所以△BHE≌△DGF.
证明:(1)∵P在CD的垂直平分线上,
∴PC=PD.
又∵OP=OP,
∴Rt△OPC≌Rt△OPD(HL).
∴OC=OD.
(2)由(1)Rt△OPC≌△OPD知∠AOP=∠BOP.
解:(1)∵DE是AB的垂直平分线,
∴AE=BE,
∴∠A=∠ABE=38°
∵AB=AC,
∴∠ABC=∠C=71°
∴∠EBC=∠ABC-∠ABE=71°-38°=33°
(2)由△ABC的周长为36cm
AB>BC,AB=AC
可知AB=AC=13cm BC=10cm
△BCE的周长=BE+CE+BC=AC+BC=13+10=23(cm)
解:(1)如图,点D为所作;
(2)∵DA=DB,
∴∠DAB=∠B=37°,
∵∠BAC=∠C﹣∠B=90°﹣37°=53°,
∴∠CAD=53°﹣37°=16°.
证明:如图,延长AD交BC于点F,
∵BE是角平分线,AD⊥BE,
∴△ABF是等腰三角形,且∠2=∠AFB,
又∵∠AFB=∠1+∠C,
∴∠2=∠1+∠C.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
