2022-2023学年浙教版数学九年级上册3.7 正多边形 课时练习(含答案)
文档属性
| 名称 | 2022-2023学年浙教版数学九年级上册3.7 正多边形 课时练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 244.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 13:35:11 | ||
图片预览



文档简介
2022-2023年浙教版数学九年级上册3.7
《正多边形》课时练习
一 、选择题
1.已知正六边形的边长为2,则它的内切圆的半径为( )
A.1 B. C.2 D.2
2.下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
3.如图,P,Q分别是⊙O的内接正五边形的边AB,BC上的点,BP=CQ,则∠POQ=( )
A.75° B.54° C.72° D.60°
4.圆的半径扩大一倍,则它的相应的圆内接正n边形的边长与半径之比( )
A.扩大了一倍 B.扩大了两倍 C.扩大了四倍 D.没有变化
5.如果一个正多边形绕着它的中心旋转60°后,能与原正多边形重合,那么这个正多边形( )
A.是轴对称图形,但不是中心对称图形
B.是中心对称图形,但不是轴对称图形
C.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
6.已知圆的半径是2,则该圆的内接正六边形的面积是( )
A.3 B.9 C.18 D.36
7.如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM和的长分别为( )
A.2, B.2,π C., D.2,
8.以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A. B. C. D.
9.正三角形内切圆半径r与外接圆半径R之间的关系为( )
A.4R=5r B.3R=4r C.2R=3r D.R=2r
10.如图,边长为a的正六边形内有一边长为a的正三角形,则=( )
A.3 B.4 C.5 D.6
二 、填空题
11.同一个圆的内接正方形和正三角形的边心距的比为 .
12.已知圆的半径是6,则圆内接正三角形的边长是 .
13.如图,正六边形ABCDEF内接于半径为4的圆,则B、E两点间的距离为 .
14.如图,在⊙O的内接五边形ABCDE中,∠CAD=30°,则∠B+∠E= .
15.如图,在正六边形ABCDEF中,连接对角线AC,CE,DF,EA,FB,可以得到一个六角星.记这些对角线的交点分别为H,I,J,K,L、M,则图中等边三角形共有 个.
16.小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他绘制了如图2所示的图形.图2中六个形状大小都相同的四边形围成一个圆的内接正六边形和一个小正六边形,若PQ所在的直线经过点M,PB=5 cm,小正六边形的面积为 cm2,则该圆的半径为______cm.
三 、解答题
17.如图,已知正五边形ABCDE,M是CD的中点,连接AC,BE,AM.
求证:(1)AC=BE;(2)AM⊥CD.
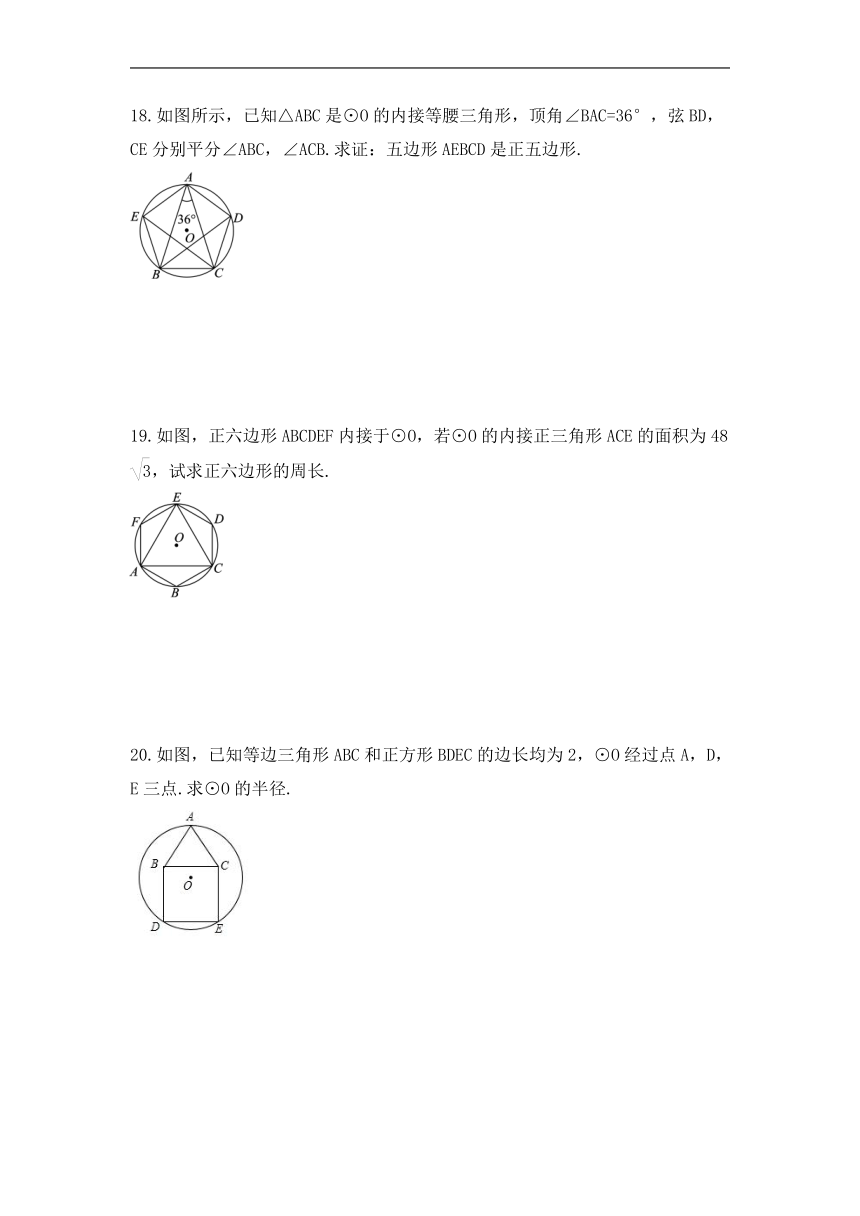
18.如图所示,已知△ABC是⊙O的内接等腰三角形,顶角∠BAC=36°,弦BD,CE分别平分∠ABC,∠ACB.求证:五边形AEBCD是正五边形.
19.如图,正六边形ABCDEF内接于⊙O,若⊙O的内接正三角形ACE的面积为48 ,试求正六边形的周长.
20.如图,已知等边三角形ABC和正方形BDEC的边长均为2,⊙O经过点A,D,E三点.求⊙O的半径.
21.如图正方形ABCD内接于⊙O,E为CD任意一点,连接DE、AE.
(1)求∠AED的度数.
(2)如图2,过点B作BF∥DE交⊙O于点F,连接AF,AF=1,AE=4,求DE的长度.
参考答案
1.B.
2.A
3.C
4.D
5.C
6.C
7.D
8.A
9.D
10.C
11.答案为::1.
12.答案为:6.
13.答案为:8.
14.答案为:210°.
15.答案为:8.
16.答案为:8
17.证明:(1)由五边形ABCDE是正五边形,得AB=AE,∠ABC=∠BAE,AB=BC,
∴△ABC≌△EAB,∴AC=BE.
(2)连接AD,由五边形ABCDE是正五边形,得AB=AE,∠ABC=∠AED,BC=ED,
∴△ABC≌△AED,
∴AC=AD.
又∵M是CD的中点,
∴AM⊥CD.
18.证明:∵△ABC是等腰三角形,且∠BAC=36°,
∴∠ABC=∠ACB=72°.
又∵BD平分∠ABC,CE平分∠ACB,
∴∠ABD=∠CBD=∠BCE=∠ACE=36°,
即∠BAC=∠ABD=∠CBD=∠BCE=∠ACE,
∴====,
∴A,E,B,C,D是⊙O的五等分点,
∴五边形AEBCD是正五边形.
19.解:如图,连接OA,作OH⊥AC于点H,则∠OAH=30°.
在Rt△OAH中,设OA=R,则OH=R,
由勾股定理可得AH=== R.
而△ACE的面积是△OAH面积的6倍,
即6×× R×R=48 ,解得R=8,
即正六边形的边长为8,所以正六边形的周长为48.
20.解:如图,作AF⊥BC,垂足为F,并延长AF交DE于H点.
∵△ABC为等边三角形,
∴AF垂直平分BC,
∵四边形BDEC为正方形,
∴AH垂直平分正方形的边DE.
又∵DE是圆的弦,
∴AH必过圆心,记圆心为O点,并设⊙O的半径为r.
在Rt△ABF中,∵∠BAF=30°,
∴AF=2×.
∴OH=AF+FH﹣OA=+2﹣r.
在Rt△ODH中,OH2+DH2=OD2.
∴(2+﹣r)2+12=r2.解得r=2.
∴该圆的半径长为2.
21.解:(1)如图1中,连接OA、OD.
∵四边形ABCD是正方形,
∴∠AOD=90°,
∴∠AED=∠AOD=45°.
(2)如图2中,连接CF,CE,CA,BD,作DH⊥AE于H.
∵BF∥DE,AB∥CD,
∴∠BDE=∠DBF,∠BDC=∠ABD,
∴∠ABF=∠CDE,
∵∠CFA=∠AEC=90°,
∴∠DEC=∠AFB=135°,
∵CD=AB,
∴△CDE≌△ABF,
∴AF=CE=1,
∴AC==,
∴AD=AC=,
∵∠DHE=90°,
∴∠HDE=∠HED=45°,
∴DH=HE,设DH=EH=x,
在Rt△ADH中,∵AD2=AH2+DH2,
∴=(4﹣x)2+x2,解得x=或(舍弃),
∴DE=DH=
《正多边形》课时练习
一 、选择题
1.已知正六边形的边长为2,则它的内切圆的半径为( )
A.1 B. C.2 D.2
2.下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
3.如图,P,Q分别是⊙O的内接正五边形的边AB,BC上的点,BP=CQ,则∠POQ=( )
A.75° B.54° C.72° D.60°
4.圆的半径扩大一倍,则它的相应的圆内接正n边形的边长与半径之比( )
A.扩大了一倍 B.扩大了两倍 C.扩大了四倍 D.没有变化
5.如果一个正多边形绕着它的中心旋转60°后,能与原正多边形重合,那么这个正多边形( )
A.是轴对称图形,但不是中心对称图形
B.是中心对称图形,但不是轴对称图形
C.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
6.已知圆的半径是2,则该圆的内接正六边形的面积是( )
A.3 B.9 C.18 D.36
7.如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM和的长分别为( )
A.2, B.2,π C., D.2,
8.以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A. B. C. D.
9.正三角形内切圆半径r与外接圆半径R之间的关系为( )
A.4R=5r B.3R=4r C.2R=3r D.R=2r
10.如图,边长为a的正六边形内有一边长为a的正三角形,则=( )
A.3 B.4 C.5 D.6
二 、填空题
11.同一个圆的内接正方形和正三角形的边心距的比为 .
12.已知圆的半径是6,则圆内接正三角形的边长是 .
13.如图,正六边形ABCDEF内接于半径为4的圆,则B、E两点间的距离为 .
14.如图,在⊙O的内接五边形ABCDE中,∠CAD=30°,则∠B+∠E= .
15.如图,在正六边形ABCDEF中,连接对角线AC,CE,DF,EA,FB,可以得到一个六角星.记这些对角线的交点分别为H,I,J,K,L、M,则图中等边三角形共有 个.
16.小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他绘制了如图2所示的图形.图2中六个形状大小都相同的四边形围成一个圆的内接正六边形和一个小正六边形,若PQ所在的直线经过点M,PB=5 cm,小正六边形的面积为 cm2,则该圆的半径为______cm.
三 、解答题
17.如图,已知正五边形ABCDE,M是CD的中点,连接AC,BE,AM.
求证:(1)AC=BE;(2)AM⊥CD.
18.如图所示,已知△ABC是⊙O的内接等腰三角形,顶角∠BAC=36°,弦BD,CE分别平分∠ABC,∠ACB.求证:五边形AEBCD是正五边形.
19.如图,正六边形ABCDEF内接于⊙O,若⊙O的内接正三角形ACE的面积为48 ,试求正六边形的周长.
20.如图,已知等边三角形ABC和正方形BDEC的边长均为2,⊙O经过点A,D,E三点.求⊙O的半径.
21.如图正方形ABCD内接于⊙O,E为CD任意一点,连接DE、AE.
(1)求∠AED的度数.
(2)如图2,过点B作BF∥DE交⊙O于点F,连接AF,AF=1,AE=4,求DE的长度.
参考答案
1.B.
2.A
3.C
4.D
5.C
6.C
7.D
8.A
9.D
10.C
11.答案为::1.
12.答案为:6.
13.答案为:8.
14.答案为:210°.
15.答案为:8.
16.答案为:8
17.证明:(1)由五边形ABCDE是正五边形,得AB=AE,∠ABC=∠BAE,AB=BC,
∴△ABC≌△EAB,∴AC=BE.
(2)连接AD,由五边形ABCDE是正五边形,得AB=AE,∠ABC=∠AED,BC=ED,
∴△ABC≌△AED,
∴AC=AD.
又∵M是CD的中点,
∴AM⊥CD.
18.证明:∵△ABC是等腰三角形,且∠BAC=36°,
∴∠ABC=∠ACB=72°.
又∵BD平分∠ABC,CE平分∠ACB,
∴∠ABD=∠CBD=∠BCE=∠ACE=36°,
即∠BAC=∠ABD=∠CBD=∠BCE=∠ACE,
∴====,
∴A,E,B,C,D是⊙O的五等分点,
∴五边形AEBCD是正五边形.
19.解:如图,连接OA,作OH⊥AC于点H,则∠OAH=30°.
在Rt△OAH中,设OA=R,则OH=R,
由勾股定理可得AH=== R.
而△ACE的面积是△OAH面积的6倍,
即6×× R×R=48 ,解得R=8,
即正六边形的边长为8,所以正六边形的周长为48.
20.解:如图,作AF⊥BC,垂足为F,并延长AF交DE于H点.
∵△ABC为等边三角形,
∴AF垂直平分BC,
∵四边形BDEC为正方形,
∴AH垂直平分正方形的边DE.
又∵DE是圆的弦,
∴AH必过圆心,记圆心为O点,并设⊙O的半径为r.
在Rt△ABF中,∵∠BAF=30°,
∴AF=2×.
∴OH=AF+FH﹣OA=+2﹣r.
在Rt△ODH中,OH2+DH2=OD2.
∴(2+﹣r)2+12=r2.解得r=2.
∴该圆的半径长为2.
21.解:(1)如图1中,连接OA、OD.
∵四边形ABCD是正方形,
∴∠AOD=90°,
∴∠AED=∠AOD=45°.
(2)如图2中,连接CF,CE,CA,BD,作DH⊥AE于H.
∵BF∥DE,AB∥CD,
∴∠BDE=∠DBF,∠BDC=∠ABD,
∴∠ABF=∠CDE,
∵∠CFA=∠AEC=90°,
∴∠DEC=∠AFB=135°,
∵CD=AB,
∴△CDE≌△ABF,
∴AF=CE=1,
∴AC==,
∴AD=AC=,
∵∠DHE=90°,
∴∠HDE=∠HED=45°,
∴DH=HE,设DH=EH=x,
在Rt△ADH中,∵AD2=AH2+DH2,
∴=(4﹣x)2+x2,解得x=或(舍弃),
∴DE=DH=
同课章节目录
