浙教版八年级数学上册1.5三角形全等的判定(1-4)提升学案(含答案)
文档属性
| 名称 | 浙教版八年级数学上册1.5三角形全等的判定(1-4)提升学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 378.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 16:49:49 | ||
图片预览



文档简介
浙教版-8年级-上册-数学-第1章《三角形的初步知识》
1.5三角形全等的判定(一)SSS
【知识点-部分】
一、三角形的稳定性
1、当三角形的三条边长确定时,三角形的形状、大小完全被确定,这个性质叫做三角形的稳定性.
要点诠释:
(1)三角形的形状固定是指三角形的三个内角不会改变,大小固定指三条边长不改变;
(2)三角形的稳定性在生产和生活中很有用.例如,房屋的人字梁具有三角形的结构,它就坚固而稳定;在栅栏门上斜着钉一条(或两条)木板,构成一个三角形,就可以使栅栏门不变形.大桥钢架、输电线支架都采用三角形结构,也是这个道理;
(3)四边形没有稳定性,也就是说,四边形的四条边长确定后,不能确定它的形状,它的各个角的大小可以改变。四边形的不稳定性也有广泛应用,如活动挂架,伸缩尺.有时我们又要克服四边形的不稳定性,如在门框未安好之前,先在门框上斜着钉一根木板,使它不变形。
二、全等三角形判定1——“边边边”
1、三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS”).
要点诠释:如图,如果=AB,=AC,=BC,则△ABC≌△.
三、全等三角形判定2——“边角边”
(1)两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”).
要点诠释:如图,如果AB = ,∠A=∠,AC = ,则△ABC≌△。
注意:这里的角,指的是两组对应边的夹角。
2、有两边和其中一边的对角对应相等,两个三角形不一定全等.
(1)如图,△ABC与△ABD中,AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等。
四、线段的垂直平分线
1、定义:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫线段的中垂线。
2、线段的垂直平分线的尺规作图:求做线段AB的垂直平分线
作法:(1)分别以点A,B为圆心,以大于AB的长为半径作弧,两弧相交于C,D两点;
(2)作直线CD,CD即为所求直线.
要点诠释:作弧时的半径必须大于AB的长,否则就不能得到交点了。
3、线段的垂直平分线性质定理:线段垂直平分线上的任意一点到这条线段两个端点的距离相等.
要点诠释:线段的垂直平分线性质定理,是证明两线段相等的常用方法之一。同时也给出了引辅助线的方法,那就是遇见线段的垂直平分线,画出到线段两个端点的距离,这样就出现相等线段,直接或间接地为构造全等三角
形创造条件。
五、全等三角形判定3——“角边角”
1、两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”)。
要点诠释:如图,如果∠A=∠,AB=,∠B=∠,则△ABC≌△。
六、全等三角形判定4——“角角边”
两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)
要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论。
1、三个角对应相等的两个三角形不一定全等.
(1)如图,在△ABC和△ADE中,如果DE∥BC,那么∠ADE=∠B,∠AED=∠C,又∠A=∠A,但△ABC和△ADE
不全等.这说明,三个角对应相等的两个三角形不一定全等。
2、角平分线的性质定理:角平分线上的点到角两边的距离相等.
要点诠释:(1)用符号语言表示角的平分线的性质定理:
(2)若CD平分∠ADB,点P是CD上一点,且PE⊥AD于点E,PF⊥BD于点F,则PE=PF。
4、角平分线的尺规作图
(1)以O为圆心,适当长为半径画弧,交OA于D,交OB于E.
(2)分别以D、E为圆心,大于DE的长为半径画弧,两弧在∠AOB内部交于点C.
(3)画射线OC; (4)射线OC即为所求.
【典型例题-精选部分】
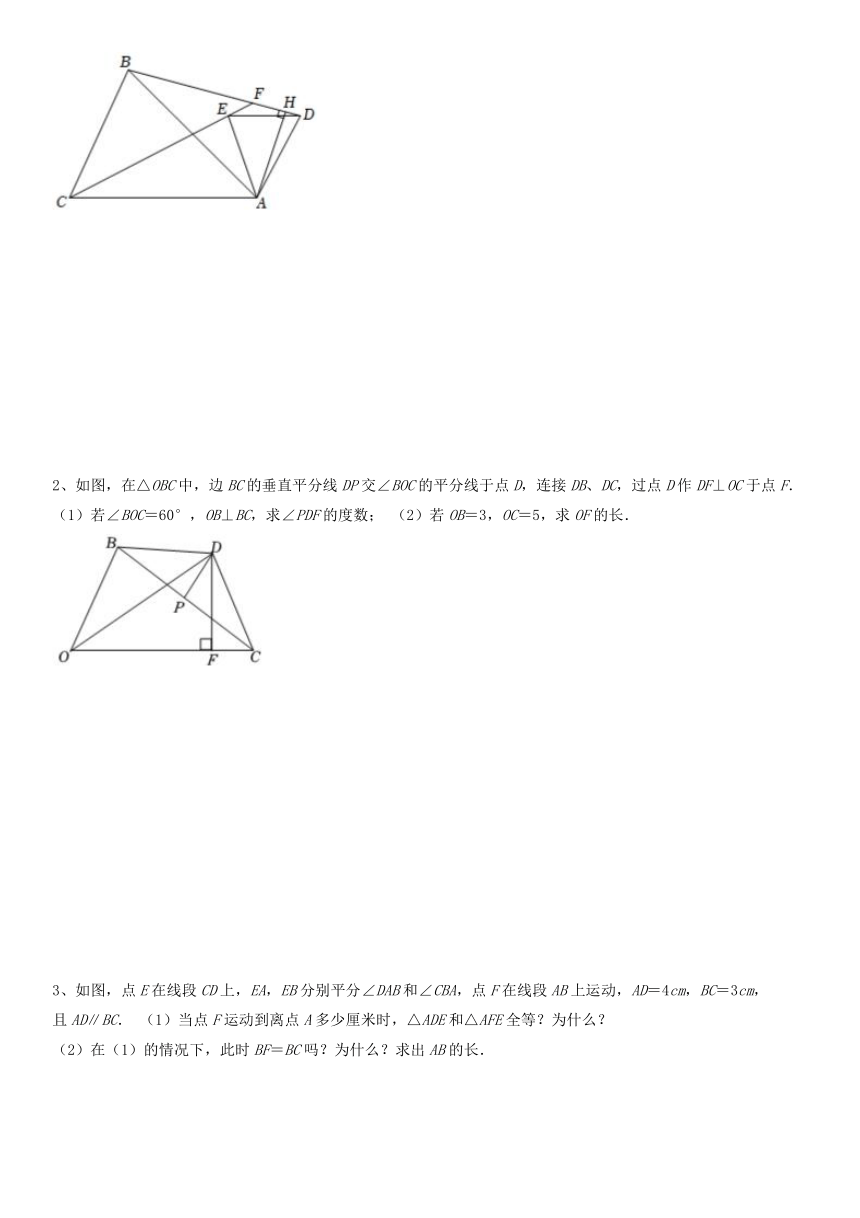
1、综合与探究:如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,CE的延长线交BD于点F.
(1)求证:△ACE≌△ABD. (2)若∠BAC=∠DAE=50°,请直接写出∠BFC的度数.
(3)过点A作AH⊥BD于点H,求证:EF+DH=HF.
2、如图,在△OBC中,边BC的垂直平分线DP交∠BOC的平分线于点D,连接DB、DC,过点D作DF⊥OC于点F.
(1)若∠BOC=60°,OB⊥BC,求∠PDF的度数; (2)若OB=3,OC=5,求OF的长.
3、如图,点E在线段CD上,EA,EB分别平分∠DAB和∠CBA,点F在线段AB上运动,AD=4cm,BC=3cm,
且AD∥BC. (1)当点F运动到离点A多少厘米时,△ADE和△AFE全等?为什么?
(2)在(1)的情况下,此时BF=BC吗?为什么?求出AB的长.
4、如图①:△ABC中,AC=BC,延长AC到E,过点E作EF⊥AB交AB的延长线于点F,延长CB到G,
过点G作GH⊥AB交AB的延长线于H,且EF=GH.
(1)求证:△AEF≌△BGH; (2)如图②,连接EG与FH相交于点D,若AB=4,求DH的长.
5、在Rt△ABC中,∠ABC=90°,点D是CB延长线上一点,点E是线段AB上一点,连接DE.AC=DE,BC=BE.
(1)求证:AB=BD;
(2)BF平分∠ABC交AC于点F,点G是线段FB延长线上一点,连接DG,点H是线段DG上一点,连接AH交BD于点K,连接KG.当KB平分∠AKG时,求证:AK=DG+KG.
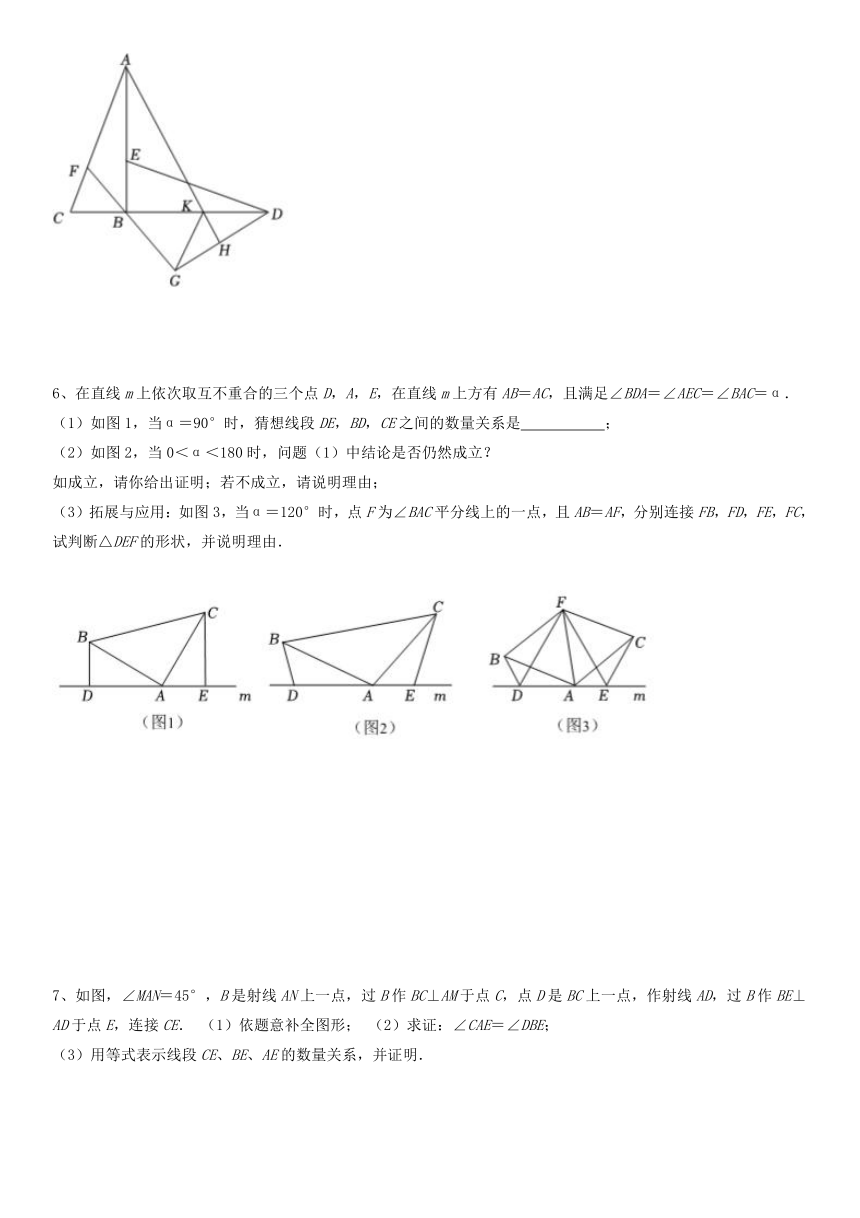
6、在直线m上依次取互不重合的三个点D,A,E,在直线m上方有AB=AC,且满足∠BDA=∠AEC=∠BAC=α.
(1)如图1,当α=90°时,猜想线段DE,BD,CE之间的数量关系是 ;
(2)如图2,当0<α<180时,问题(1)中结论是否仍然成立?
如成立,请你给出证明;若不成立,请说明理由;
(3)拓展与应用:如图3,当α=120°时,点F为∠BAC平分线上的一点,且AB=AF,分别连接FB,FD,FE,FC,试判断△DEF的形状,并说明理由.
7、如图,∠MAN=45°,B是射线AN上一点,过B作BC⊥AM于点C,点D是BC上一点,作射线AD,过B作BE⊥AD于点E,连接CE. (1)依题意补全图形; (2)求证:∠CAE=∠DBE;
(3)用等式表示线段CE、BE、AE的数量关系,并证明.
8、已知:在△ABC中,BD是边AC的高,BE为∠CBD的角平分线,且AD=DE.AO为△ABC的中线,延长AO到点F.使得BF∥AC.连接EF.EF交BC于点G.AF交BE于点H.
(1)求证:BF=CD+DE; (2)若∠C=45°.求证:BD=BG.
9、如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=α.
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上.
① 如图1,若∠BCA=90°,α=90°,则BE CF;
② 如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件 ,
使①中的结论仍然成立,并说明理由;
(2)如图3,若直线CD经过∠BCA的外部,α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并简述理由.
10、课外兴趣小组活动中,老师出示了如下问题:如图1,已知四边形ABCD中,AC平分∠DAB,∠DAB=60°,
∠B与∠D互补,求证:AB+AD=AC.
小敏反复探索,不得其解.她想,可先将四边形ABCD特殊化,再进一步解决问题.
(1)由特殊情况入手,添加条件:“∠B=∠D”,如图2,可证AB+AD=AC,请你完成此证明;
(2)受到(1)的启发,在原问题中,添加辅助线:过C点分别作AB、AD的垂线,垂足分别为E、F,如图3,请你补全证明过程.
【参考答案】
1、综合与探究:如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,CE的延长线交BD于点F.
(1)求证:△ACE≌△ABD. (2)若∠BAC=∠DAE=50°,请直接写出∠BFC的度数.
(3)过点A作AH⊥BD于点H,求证:EF+DH=HF.
【解答】证明:(1)∵∠BAC=∠DAE.∴∠CAE=∠BAD.在△ACE和△ABD中,
,∴△ACE≌△ABD(SAS);
(2)解:∵△ACE≌△ABD,∴∠AEC=∠ADB,∴∠AEF+∠AEC=∠AEF+∠ADB=180°.
∴∠DAE+∠DFE=180°,∵∠BFC+∠DFE=180°,∴∠BFC=∠DAE=∠BAC=50°;
(3)证明:如图,连接AF,过点A作AJ⊥CF于点J.∵△ACE≌△ABD,∴S△ACE=S△ABD,CE=BD,
∵AJ⊥CE,AH⊥BD.∴,∴AJ=AH.
在Rt△AFJ和Rt△AFH中,,∴Rt△AFJ≌Rt△AFH(HL),∴FJ=FH.
在Rt△AJE和Rt△AHD中,,∴Rt△AJE≌Rt△AHD(HL),∴EJ=DH,∴EF+DH=EF+EJ=FJ=FH.
2、如图,在△OBC中,边BC的垂直平分线DP交∠BOC的平分线于点D,连接DB、DC,过点D作DF⊥OC于点F.
(1)若∠BOC=60°,OB⊥BC,求∠PDF的度数; (2)若OB=3,OC=5,求OF的长.
【解答】解:(1)如图,作DE⊥OB交OB的延长线于点E,∵OD平分∠BOC,DF⊥OC,点D在BC的垂直平分线上,
∴DE=DF,∠DEB=∠DFC=90°,DB=DC,在Rt△DEB和Rt△DFC中,,∴Rt△DEB≌Rt△DFC(HL),
∴∠BDE=∠CDF,∴∠BDE+∠BDF=∠CDF+∠BDF,即∠EDF=∠BDC,∵∠OED=∠OFD=90°,∠BOC=60°,
∴∠EDF=120°,∴∠BDC=120°,∵OB⊥BC,∠BOC=60°,∴∠OCB=30°,∵DF⊥OC,PD⊥BC,
∴∠PDF=∠OCB=30°;
(2)由(1)可知:△DEB≌△DFC,∴BE=CF,∵OB+OC=OB+OF+FC,
∴OB+OC=OB+OF+EB=(OB+EB)+OF=OE+OF,∵∠DEO=∠DFO=90°,DE=DF,在Rt△DEO和Rt△DFO中,
,∴Rt△DEO≌Rt△DFO(HL),∴OE=OF,∴OB+OC=2OF.∵OB=3,OC=5,∴OF=4.
3、如图,点E在线段CD上,EA,EB分别平分∠DAB和∠CBA,点F在线段AB上运动,AD=4cm,BC=3cm,
且AD∥BC. (1)当点F运动到离点A多少厘米时,△ADE和△AFE全等?为什么?
(2)在(1)的情况下,此时BF=BC吗?为什么?求出AB的长.
【解答】解:(1)当点F运动到离点A为4cm(即AF=AD=4cm)时,△ADE≌△AFE,理由如下:
∵EA、EB分别平分∠DAB和∠CBA,∴∠DAE=∠FAE,∠FBE=∠CBE,
在△AFE与△ADE中,,∴△AFE≌△ADE(SAS);
(2)BF=BC,理由如下:∵△AFE≌△ADE,∴∠D=∠AFE,∵AD∥BC,∴∠D+∠C=180°,
∵∠AFE+∠BFE=180°,∴∠C=∠BFE,在△ECB与△EFB中,,∴△ECB≌△EFB(AAS),
∴BF=BC;∵AF=AD=4cm,BF=BC=3cm,∴AB=AF+BF=3+4=7(cm).
4、如图①:△ABC中,AC=BC,延长AC到E,过点E作EF⊥AB交AB的延长线于点F,延长CB到G,
过点G作GH⊥AB交AB的延长线于H,且EF=GH.
(1)求证:△AEF≌△BGH; (2)如图②,连接EG与FH相交于点D,若AB=4,求DH的长.
【解答】证明:(1)∵AC=BC,∴∠A=∠ABC.∵∠ABC=∠GBH,∴∠A=∠GBH.∵EF⊥AB,GH⊥AB,
∴∠AFE=∠BHG.在△ADG和△CDF中,,∴△AEF≌△BGH(AAS).
(2)解:∵△AEF≌△BGH,∴AF=BH,∴AB=FH=4.∵EF⊥AB,GH⊥AB,∴∠EFD=∠GHD.
在△EFD和△GHD中,∴△EFD≌△GHD(AAS),∴.
5、在Rt△ABC中,∠ABC=90°,点D是CB延长线上一点,点E是线段AB上一点,连接DE.AC=DE,BC=BE.
(1)求证:AB=BD;
(2)BF平分∠ABC交AC于点F,点G是线段FB延长线上一点,连接DG,点H是线段DG上一点,连接AH交BD于点K,连接KG.当KB平分∠AKG时,求证:AK=DG+KG.
【解答】证明:(1)在Rt△ACB和Rt△DEB中,,∴Rt△ACB≌Rt△DEB(HL),∴AB=BD,
(2)如图:作BM平分∠ABD交AK于点M,∵BM平分∠ABD,KB平分∠AKG,
∴∠ABM=∠MBD=45°,∠AKB=∠BKG,∵∠ABF=∠DBG=45°∴∠MBD=∠GBD,
在△BMK和△BGK中,,∴△BMK≌△BGK(ASA),∴BM=BG,MK=KG,
在△ABM和△DBG中,,∴△ABM≌△DBG(SAS),∴AM=DG,∵AK=AM+MK,∴AK=DG+KG.
6、在直线m上依次取互不重合的三个点D,A,E,在直线m上方有AB=AC,且满足∠BDA=∠AEC=∠BAC=α.
(1)如图1,当α=90°时,猜想线段DE,BD,CE之间的数量关系是 ;
(2)如图2,当0<α<180时,问题(1)中结论是否仍然成立?
如成立,请你给出证明;若不成立,请说明理由;
(3)拓展与应用:如图3,当α=120°时,点F为∠BAC平分线上的一点,且AB=AF,分别连接FB,FD,FE,FC,试判断△DEF的形状,并说明理由.
【解答】解:(1)DE=BD+CE,理由如下,∵∠BDA=∠BAC=∠AEC=90°,∴∠BAD+∠EAC=∠BAD+∠DBA=90°,
∴∠DBA=∠EAC,∵AB=AC,∴△DBA≌△EAC(AAS),∴AD=CE,BD=AE,∴DE=AD+AE=BD+CE,
故答案为:DE=BD+CE.
(2)DE=BD+CE仍然成立,理由如下,
∵∠BDA=∠BAC=∠AEC=α,∴∠BAD+∠EAC=∠BAD+∠DBA=180°﹣α,∴∠DBA=∠EAC,∵AB=AC,
∴△DBA≌△EAC(AAS),∴BD=AE,AD=CE,∴DE=AD+AE=BD+CE;
(3)△DEF是等边三角形,理由如下,
∵α=120°,AF平分∠BAC,∴∠BAF=∠CAF=60°,∵AB=AF=AC,∴△ABF和△ACF是等边三角形,
∴FA=FC,∠FCA=∠FAB=∠AFC=60°,同(2)可得,△BDA≌△AEC,∴∠BAD=∠ACE,AD=CE,
∴∠FAD=∠FCE,∴△FAD≌△FCE(SAS),∴DF=EF,∠DFA=∠EFC,
∴∠DFE=∠DFA+∠AFE=∠EFC+∠AFE=∠AFC=60°,∴△DEF是等边三角形.
7、如图,∠MAN=45°,B是射线AN上一点,过B作BC⊥AM于点C,点D是BC上一点,作射线AD,过B作BE⊥AD于点E,连接CE. (1)依题意补全图形; (2)求证:∠CAE=∠DBE;
(3)用等式表示线段CE、BE、AE的数量关系,并证明.
【解答】解:(1)如图,即为补全的图形;
(2)证明:∵BC⊥AM,BE⊥AD,∴∠ACB=∠BED=90°,∵∠ADC=∠BDE,∴∠CAE=∠DBE;
(3)AE=BE+CE.
证明:如图,在AE上截取AF=BE,连接CF,∵BC⊥AM,∠MAN=45°,∴∠CBA=45°,
∴△CBA是等腰直角三角形,∴CA=CB,在△CAF和△CBE中,,∴△CAF≌△CBE(SAS),
∴CF=CE,∠ACF=∠BCE,∴∠ACF+∠FCD=∠BCE+∠FCD,∴∠ACD=∠FCE=90°,
∴△FCE是等腰直角三角形,∴EF=CE,∴AE=AF+EF=BE+CE.
8、已知:在△ABC中,BD是边AC的高,BE为∠CBD的角平分线,且AD=DE.AO为△ABC的中线,延长AO到点F.使得BF∥AC.连接EF.EF交BC于点G.AF交BE于点H.
(1)求证:BF=CD+DE; (2)若∠C=45°.求证:BD=BG.
【解答】证明:(1)∵BF∥AC,∴∠BFO=∠CAO,∠FBO=∠ACO,又∵AO为△ABC的中线,∴BO=CO,
在△BOF与△COA中,,∴△BOF≌△COA(AAS),∴BF=CA=CD+AD,∵AD=DE,∴BF=CD+DE;
(2)∵BD垂直平分AE,∴BA=BE,∠BAC=∠BEA,又∵BF∥AC,∴∠BEA=∠EBF=∠BAC,
在△BAC与△EBF中,,∴△BAC≌△EBF(SAS),∴∠BFE=∠C=45°,
又∵∠BGE=∠C+∠FEC=90°=∠BDE,在△BEG与△BED中,,
∴△BEG≌△BED(AAS),∴BG=BD.
9、如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=α.
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上.
① 如图1,若∠BCA=90°,α=90°,则BE CF;
② 如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件 ,
使①中的结论仍然成立,并说明理由;
(2)如图3,若直线CD经过∠BCA的外部,α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并简述理由.
【解答】解:(1)① ∵∠BEC=∠CFA=α=90°,∴∠BCE+∠CBE=180°﹣∠BEC=90°.
又∵∠BCA=∠BCE+∠ACF=90°,∴∠CBE=∠ACF.在△BCE和△CAF中,
∴△BCE≌△CAF(AAS).∴BE=CF.
② α+∠BCA=180°,理由如下:∵∠BEC=∠CFA=α,∴∠BEF=180°﹣∠BEC=180°﹣α.
又∵∠BEF=∠EBC+∠BCE,∴∠EBC+∠BCE=180°﹣α.又∵α+∠BCA=180°,∴∠BCA=180°﹣α.
∴∠BCA=∠BCE+∠ACF=180°﹣α.∴∠EBC=∠FCA.
在△BCE和△CAF中,∴△BCE≌△CAF(AAS).∴BE=CF.
(2)EF=BE+AF,理由如下:
∵∠BCA=α,∴∠BCE+∠ACF=180°﹣∠BCA=180°﹣α.又∵∠BEC=α,
∴∠EBC+∠BCE=180°﹣∠BEC=180°﹣α.∴∠EBC=∠FCA.
在△BEC和△CFA中,∴△BEC≌△CFA(AAS).
∴BE=CF,EC=FA.∴EF=EC+CF=FA+BE,即EF=BE+AF.
10、课外兴趣小组活动中,老师出示了如下问题:如图1,已知四边形ABCD中,AC平分∠DAB,∠DAB=60°,
∠B与∠D互补,求证:AB+AD=AC.
小敏反复探索,不得其解.她想,可先将四边形ABCD特殊化,再进一步解决问题.
(1)由特殊情况入手,添加条件:“∠B=∠D”,如图2,可证AB+AD=AC,请你完成此证明;
(2)受到(1)的启发,在原问题中,添加辅助线:过C点分别作AB、AD的垂线,垂足分别为E、F,如图3,请你补全证明过程.
【解答】证明:(1)∵∠B与∠D互补,∠B=∠D,∴∠B=∠D=90°,∵AC平分∠DAB
∴∠CAD=∠CAB=∠DAB=30°,在△ADC中,cos30°=,在△ABC中,cos30°=,
∴AB=AC,AD=AC.∴AB+AD=AC.
(2)由(1)知,AE+AF=AC,∵AC为角平分线,CF⊥AD,CE⊥AB,∴CE=CF.而∠ABC与∠D互补,
∠ABC与∠CBE也互补,∴∠D=∠CBE.在Rt△CDF与Rt△CBE中,,∴Rt△CDF≌Rt△CBE(AAS).
∴DF=BE.∴AB+AD=AB+(AF+FD)=(AB+BE)+AF=AE+AF=AC.
1.5三角形全等的判定(一)SSS
【知识点-部分】
一、三角形的稳定性
1、当三角形的三条边长确定时,三角形的形状、大小完全被确定,这个性质叫做三角形的稳定性.
要点诠释:
(1)三角形的形状固定是指三角形的三个内角不会改变,大小固定指三条边长不改变;
(2)三角形的稳定性在生产和生活中很有用.例如,房屋的人字梁具有三角形的结构,它就坚固而稳定;在栅栏门上斜着钉一条(或两条)木板,构成一个三角形,就可以使栅栏门不变形.大桥钢架、输电线支架都采用三角形结构,也是这个道理;
(3)四边形没有稳定性,也就是说,四边形的四条边长确定后,不能确定它的形状,它的各个角的大小可以改变。四边形的不稳定性也有广泛应用,如活动挂架,伸缩尺.有时我们又要克服四边形的不稳定性,如在门框未安好之前,先在门框上斜着钉一根木板,使它不变形。
二、全等三角形判定1——“边边边”
1、三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS”).
要点诠释:如图,如果=AB,=AC,=BC,则△ABC≌△.
三、全等三角形判定2——“边角边”
(1)两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”).
要点诠释:如图,如果AB = ,∠A=∠,AC = ,则△ABC≌△。
注意:这里的角,指的是两组对应边的夹角。
2、有两边和其中一边的对角对应相等,两个三角形不一定全等.
(1)如图,△ABC与△ABD中,AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等。
四、线段的垂直平分线
1、定义:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫线段的中垂线。
2、线段的垂直平分线的尺规作图:求做线段AB的垂直平分线
作法:(1)分别以点A,B为圆心,以大于AB的长为半径作弧,两弧相交于C,D两点;
(2)作直线CD,CD即为所求直线.
要点诠释:作弧时的半径必须大于AB的长,否则就不能得到交点了。
3、线段的垂直平分线性质定理:线段垂直平分线上的任意一点到这条线段两个端点的距离相等.
要点诠释:线段的垂直平分线性质定理,是证明两线段相等的常用方法之一。同时也给出了引辅助线的方法,那就是遇见线段的垂直平分线,画出到线段两个端点的距离,这样就出现相等线段,直接或间接地为构造全等三角
形创造条件。
五、全等三角形判定3——“角边角”
1、两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”)。
要点诠释:如图,如果∠A=∠,AB=,∠B=∠,则△ABC≌△。
六、全等三角形判定4——“角角边”
两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)
要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论。
1、三个角对应相等的两个三角形不一定全等.
(1)如图,在△ABC和△ADE中,如果DE∥BC,那么∠ADE=∠B,∠AED=∠C,又∠A=∠A,但△ABC和△ADE
不全等.这说明,三个角对应相等的两个三角形不一定全等。
2、角平分线的性质定理:角平分线上的点到角两边的距离相等.
要点诠释:(1)用符号语言表示角的平分线的性质定理:
(2)若CD平分∠ADB,点P是CD上一点,且PE⊥AD于点E,PF⊥BD于点F,则PE=PF。
4、角平分线的尺规作图
(1)以O为圆心,适当长为半径画弧,交OA于D,交OB于E.
(2)分别以D、E为圆心,大于DE的长为半径画弧,两弧在∠AOB内部交于点C.
(3)画射线OC; (4)射线OC即为所求.
【典型例题-精选部分】
1、综合与探究:如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,CE的延长线交BD于点F.
(1)求证:△ACE≌△ABD. (2)若∠BAC=∠DAE=50°,请直接写出∠BFC的度数.
(3)过点A作AH⊥BD于点H,求证:EF+DH=HF.
2、如图,在△OBC中,边BC的垂直平分线DP交∠BOC的平分线于点D,连接DB、DC,过点D作DF⊥OC于点F.
(1)若∠BOC=60°,OB⊥BC,求∠PDF的度数; (2)若OB=3,OC=5,求OF的长.
3、如图,点E在线段CD上,EA,EB分别平分∠DAB和∠CBA,点F在线段AB上运动,AD=4cm,BC=3cm,
且AD∥BC. (1)当点F运动到离点A多少厘米时,△ADE和△AFE全等?为什么?
(2)在(1)的情况下,此时BF=BC吗?为什么?求出AB的长.
4、如图①:△ABC中,AC=BC,延长AC到E,过点E作EF⊥AB交AB的延长线于点F,延长CB到G,
过点G作GH⊥AB交AB的延长线于H,且EF=GH.
(1)求证:△AEF≌△BGH; (2)如图②,连接EG与FH相交于点D,若AB=4,求DH的长.
5、在Rt△ABC中,∠ABC=90°,点D是CB延长线上一点,点E是线段AB上一点,连接DE.AC=DE,BC=BE.
(1)求证:AB=BD;
(2)BF平分∠ABC交AC于点F,点G是线段FB延长线上一点,连接DG,点H是线段DG上一点,连接AH交BD于点K,连接KG.当KB平分∠AKG时,求证:AK=DG+KG.
6、在直线m上依次取互不重合的三个点D,A,E,在直线m上方有AB=AC,且满足∠BDA=∠AEC=∠BAC=α.
(1)如图1,当α=90°时,猜想线段DE,BD,CE之间的数量关系是 ;
(2)如图2,当0<α<180时,问题(1)中结论是否仍然成立?
如成立,请你给出证明;若不成立,请说明理由;
(3)拓展与应用:如图3,当α=120°时,点F为∠BAC平分线上的一点,且AB=AF,分别连接FB,FD,FE,FC,试判断△DEF的形状,并说明理由.
7、如图,∠MAN=45°,B是射线AN上一点,过B作BC⊥AM于点C,点D是BC上一点,作射线AD,过B作BE⊥AD于点E,连接CE. (1)依题意补全图形; (2)求证:∠CAE=∠DBE;
(3)用等式表示线段CE、BE、AE的数量关系,并证明.
8、已知:在△ABC中,BD是边AC的高,BE为∠CBD的角平分线,且AD=DE.AO为△ABC的中线,延长AO到点F.使得BF∥AC.连接EF.EF交BC于点G.AF交BE于点H.
(1)求证:BF=CD+DE; (2)若∠C=45°.求证:BD=BG.
9、如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=α.
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上.
① 如图1,若∠BCA=90°,α=90°,则BE CF;
② 如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件 ,
使①中的结论仍然成立,并说明理由;
(2)如图3,若直线CD经过∠BCA的外部,α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并简述理由.
10、课外兴趣小组活动中,老师出示了如下问题:如图1,已知四边形ABCD中,AC平分∠DAB,∠DAB=60°,
∠B与∠D互补,求证:AB+AD=AC.
小敏反复探索,不得其解.她想,可先将四边形ABCD特殊化,再进一步解决问题.
(1)由特殊情况入手,添加条件:“∠B=∠D”,如图2,可证AB+AD=AC,请你完成此证明;
(2)受到(1)的启发,在原问题中,添加辅助线:过C点分别作AB、AD的垂线,垂足分别为E、F,如图3,请你补全证明过程.
【参考答案】
1、综合与探究:如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,CE的延长线交BD于点F.
(1)求证:△ACE≌△ABD. (2)若∠BAC=∠DAE=50°,请直接写出∠BFC的度数.
(3)过点A作AH⊥BD于点H,求证:EF+DH=HF.
【解答】证明:(1)∵∠BAC=∠DAE.∴∠CAE=∠BAD.在△ACE和△ABD中,
,∴△ACE≌△ABD(SAS);
(2)解:∵△ACE≌△ABD,∴∠AEC=∠ADB,∴∠AEF+∠AEC=∠AEF+∠ADB=180°.
∴∠DAE+∠DFE=180°,∵∠BFC+∠DFE=180°,∴∠BFC=∠DAE=∠BAC=50°;
(3)证明:如图,连接AF,过点A作AJ⊥CF于点J.∵△ACE≌△ABD,∴S△ACE=S△ABD,CE=BD,
∵AJ⊥CE,AH⊥BD.∴,∴AJ=AH.
在Rt△AFJ和Rt△AFH中,,∴Rt△AFJ≌Rt△AFH(HL),∴FJ=FH.
在Rt△AJE和Rt△AHD中,,∴Rt△AJE≌Rt△AHD(HL),∴EJ=DH,∴EF+DH=EF+EJ=FJ=FH.
2、如图,在△OBC中,边BC的垂直平分线DP交∠BOC的平分线于点D,连接DB、DC,过点D作DF⊥OC于点F.
(1)若∠BOC=60°,OB⊥BC,求∠PDF的度数; (2)若OB=3,OC=5,求OF的长.
【解答】解:(1)如图,作DE⊥OB交OB的延长线于点E,∵OD平分∠BOC,DF⊥OC,点D在BC的垂直平分线上,
∴DE=DF,∠DEB=∠DFC=90°,DB=DC,在Rt△DEB和Rt△DFC中,,∴Rt△DEB≌Rt△DFC(HL),
∴∠BDE=∠CDF,∴∠BDE+∠BDF=∠CDF+∠BDF,即∠EDF=∠BDC,∵∠OED=∠OFD=90°,∠BOC=60°,
∴∠EDF=120°,∴∠BDC=120°,∵OB⊥BC,∠BOC=60°,∴∠OCB=30°,∵DF⊥OC,PD⊥BC,
∴∠PDF=∠OCB=30°;
(2)由(1)可知:△DEB≌△DFC,∴BE=CF,∵OB+OC=OB+OF+FC,
∴OB+OC=OB+OF+EB=(OB+EB)+OF=OE+OF,∵∠DEO=∠DFO=90°,DE=DF,在Rt△DEO和Rt△DFO中,
,∴Rt△DEO≌Rt△DFO(HL),∴OE=OF,∴OB+OC=2OF.∵OB=3,OC=5,∴OF=4.
3、如图,点E在线段CD上,EA,EB分别平分∠DAB和∠CBA,点F在线段AB上运动,AD=4cm,BC=3cm,
且AD∥BC. (1)当点F运动到离点A多少厘米时,△ADE和△AFE全等?为什么?
(2)在(1)的情况下,此时BF=BC吗?为什么?求出AB的长.
【解答】解:(1)当点F运动到离点A为4cm(即AF=AD=4cm)时,△ADE≌△AFE,理由如下:
∵EA、EB分别平分∠DAB和∠CBA,∴∠DAE=∠FAE,∠FBE=∠CBE,
在△AFE与△ADE中,,∴△AFE≌△ADE(SAS);
(2)BF=BC,理由如下:∵△AFE≌△ADE,∴∠D=∠AFE,∵AD∥BC,∴∠D+∠C=180°,
∵∠AFE+∠BFE=180°,∴∠C=∠BFE,在△ECB与△EFB中,,∴△ECB≌△EFB(AAS),
∴BF=BC;∵AF=AD=4cm,BF=BC=3cm,∴AB=AF+BF=3+4=7(cm).
4、如图①:△ABC中,AC=BC,延长AC到E,过点E作EF⊥AB交AB的延长线于点F,延长CB到G,
过点G作GH⊥AB交AB的延长线于H,且EF=GH.
(1)求证:△AEF≌△BGH; (2)如图②,连接EG与FH相交于点D,若AB=4,求DH的长.
【解答】证明:(1)∵AC=BC,∴∠A=∠ABC.∵∠ABC=∠GBH,∴∠A=∠GBH.∵EF⊥AB,GH⊥AB,
∴∠AFE=∠BHG.在△ADG和△CDF中,,∴△AEF≌△BGH(AAS).
(2)解:∵△AEF≌△BGH,∴AF=BH,∴AB=FH=4.∵EF⊥AB,GH⊥AB,∴∠EFD=∠GHD.
在△EFD和△GHD中,∴△EFD≌△GHD(AAS),∴.
5、在Rt△ABC中,∠ABC=90°,点D是CB延长线上一点,点E是线段AB上一点,连接DE.AC=DE,BC=BE.
(1)求证:AB=BD;
(2)BF平分∠ABC交AC于点F,点G是线段FB延长线上一点,连接DG,点H是线段DG上一点,连接AH交BD于点K,连接KG.当KB平分∠AKG时,求证:AK=DG+KG.
【解答】证明:(1)在Rt△ACB和Rt△DEB中,,∴Rt△ACB≌Rt△DEB(HL),∴AB=BD,
(2)如图:作BM平分∠ABD交AK于点M,∵BM平分∠ABD,KB平分∠AKG,
∴∠ABM=∠MBD=45°,∠AKB=∠BKG,∵∠ABF=∠DBG=45°∴∠MBD=∠GBD,
在△BMK和△BGK中,,∴△BMK≌△BGK(ASA),∴BM=BG,MK=KG,
在△ABM和△DBG中,,∴△ABM≌△DBG(SAS),∴AM=DG,∵AK=AM+MK,∴AK=DG+KG.
6、在直线m上依次取互不重合的三个点D,A,E,在直线m上方有AB=AC,且满足∠BDA=∠AEC=∠BAC=α.
(1)如图1,当α=90°时,猜想线段DE,BD,CE之间的数量关系是 ;
(2)如图2,当0<α<180时,问题(1)中结论是否仍然成立?
如成立,请你给出证明;若不成立,请说明理由;
(3)拓展与应用:如图3,当α=120°时,点F为∠BAC平分线上的一点,且AB=AF,分别连接FB,FD,FE,FC,试判断△DEF的形状,并说明理由.
【解答】解:(1)DE=BD+CE,理由如下,∵∠BDA=∠BAC=∠AEC=90°,∴∠BAD+∠EAC=∠BAD+∠DBA=90°,
∴∠DBA=∠EAC,∵AB=AC,∴△DBA≌△EAC(AAS),∴AD=CE,BD=AE,∴DE=AD+AE=BD+CE,
故答案为:DE=BD+CE.
(2)DE=BD+CE仍然成立,理由如下,
∵∠BDA=∠BAC=∠AEC=α,∴∠BAD+∠EAC=∠BAD+∠DBA=180°﹣α,∴∠DBA=∠EAC,∵AB=AC,
∴△DBA≌△EAC(AAS),∴BD=AE,AD=CE,∴DE=AD+AE=BD+CE;
(3)△DEF是等边三角形,理由如下,
∵α=120°,AF平分∠BAC,∴∠BAF=∠CAF=60°,∵AB=AF=AC,∴△ABF和△ACF是等边三角形,
∴FA=FC,∠FCA=∠FAB=∠AFC=60°,同(2)可得,△BDA≌△AEC,∴∠BAD=∠ACE,AD=CE,
∴∠FAD=∠FCE,∴△FAD≌△FCE(SAS),∴DF=EF,∠DFA=∠EFC,
∴∠DFE=∠DFA+∠AFE=∠EFC+∠AFE=∠AFC=60°,∴△DEF是等边三角形.
7、如图,∠MAN=45°,B是射线AN上一点,过B作BC⊥AM于点C,点D是BC上一点,作射线AD,过B作BE⊥AD于点E,连接CE. (1)依题意补全图形; (2)求证:∠CAE=∠DBE;
(3)用等式表示线段CE、BE、AE的数量关系,并证明.
【解答】解:(1)如图,即为补全的图形;
(2)证明:∵BC⊥AM,BE⊥AD,∴∠ACB=∠BED=90°,∵∠ADC=∠BDE,∴∠CAE=∠DBE;
(3)AE=BE+CE.
证明:如图,在AE上截取AF=BE,连接CF,∵BC⊥AM,∠MAN=45°,∴∠CBA=45°,
∴△CBA是等腰直角三角形,∴CA=CB,在△CAF和△CBE中,,∴△CAF≌△CBE(SAS),
∴CF=CE,∠ACF=∠BCE,∴∠ACF+∠FCD=∠BCE+∠FCD,∴∠ACD=∠FCE=90°,
∴△FCE是等腰直角三角形,∴EF=CE,∴AE=AF+EF=BE+CE.
8、已知:在△ABC中,BD是边AC的高,BE为∠CBD的角平分线,且AD=DE.AO为△ABC的中线,延长AO到点F.使得BF∥AC.连接EF.EF交BC于点G.AF交BE于点H.
(1)求证:BF=CD+DE; (2)若∠C=45°.求证:BD=BG.
【解答】证明:(1)∵BF∥AC,∴∠BFO=∠CAO,∠FBO=∠ACO,又∵AO为△ABC的中线,∴BO=CO,
在△BOF与△COA中,,∴△BOF≌△COA(AAS),∴BF=CA=CD+AD,∵AD=DE,∴BF=CD+DE;
(2)∵BD垂直平分AE,∴BA=BE,∠BAC=∠BEA,又∵BF∥AC,∴∠BEA=∠EBF=∠BAC,
在△BAC与△EBF中,,∴△BAC≌△EBF(SAS),∴∠BFE=∠C=45°,
又∵∠BGE=∠C+∠FEC=90°=∠BDE,在△BEG与△BED中,,
∴△BEG≌△BED(AAS),∴BG=BD.
9、如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=α.
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上.
① 如图1,若∠BCA=90°,α=90°,则BE CF;
② 如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件 ,
使①中的结论仍然成立,并说明理由;
(2)如图3,若直线CD经过∠BCA的外部,α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并简述理由.
【解答】解:(1)① ∵∠BEC=∠CFA=α=90°,∴∠BCE+∠CBE=180°﹣∠BEC=90°.
又∵∠BCA=∠BCE+∠ACF=90°,∴∠CBE=∠ACF.在△BCE和△CAF中,
∴△BCE≌△CAF(AAS).∴BE=CF.
② α+∠BCA=180°,理由如下:∵∠BEC=∠CFA=α,∴∠BEF=180°﹣∠BEC=180°﹣α.
又∵∠BEF=∠EBC+∠BCE,∴∠EBC+∠BCE=180°﹣α.又∵α+∠BCA=180°,∴∠BCA=180°﹣α.
∴∠BCA=∠BCE+∠ACF=180°﹣α.∴∠EBC=∠FCA.
在△BCE和△CAF中,∴△BCE≌△CAF(AAS).∴BE=CF.
(2)EF=BE+AF,理由如下:
∵∠BCA=α,∴∠BCE+∠ACF=180°﹣∠BCA=180°﹣α.又∵∠BEC=α,
∴∠EBC+∠BCE=180°﹣∠BEC=180°﹣α.∴∠EBC=∠FCA.
在△BEC和△CFA中,∴△BEC≌△CFA(AAS).
∴BE=CF,EC=FA.∴EF=EC+CF=FA+BE,即EF=BE+AF.
10、课外兴趣小组活动中,老师出示了如下问题:如图1,已知四边形ABCD中,AC平分∠DAB,∠DAB=60°,
∠B与∠D互补,求证:AB+AD=AC.
小敏反复探索,不得其解.她想,可先将四边形ABCD特殊化,再进一步解决问题.
(1)由特殊情况入手,添加条件:“∠B=∠D”,如图2,可证AB+AD=AC,请你完成此证明;
(2)受到(1)的启发,在原问题中,添加辅助线:过C点分别作AB、AD的垂线,垂足分别为E、F,如图3,请你补全证明过程.
【解答】证明:(1)∵∠B与∠D互补,∠B=∠D,∴∠B=∠D=90°,∵AC平分∠DAB
∴∠CAD=∠CAB=∠DAB=30°,在△ADC中,cos30°=,在△ABC中,cos30°=,
∴AB=AC,AD=AC.∴AB+AD=AC.
(2)由(1)知,AE+AF=AC,∵AC为角平分线,CF⊥AD,CE⊥AB,∴CE=CF.而∠ABC与∠D互补,
∠ABC与∠CBE也互补,∴∠D=∠CBE.在Rt△CDF与Rt△CBE中,,∴Rt△CDF≌Rt△CBE(AAS).
∴DF=BE.∴AB+AD=AB+(AF+FD)=(AB+BE)+AF=AE+AF=AC.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
