浙教版九年级数学上册第3章圆的基本性质同步达标测试题(含解析)
文档属性
| 名称 | 浙教版九年级数学上册第3章圆的基本性质同步达标测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 447.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 16:41:09 | ||
图片预览



文档简介
2022-2023学年浙教版九年级数学上册《第3章圆的基本性质》同步达标测试题(附答案)
一.选择题(共8小题,满分40分)
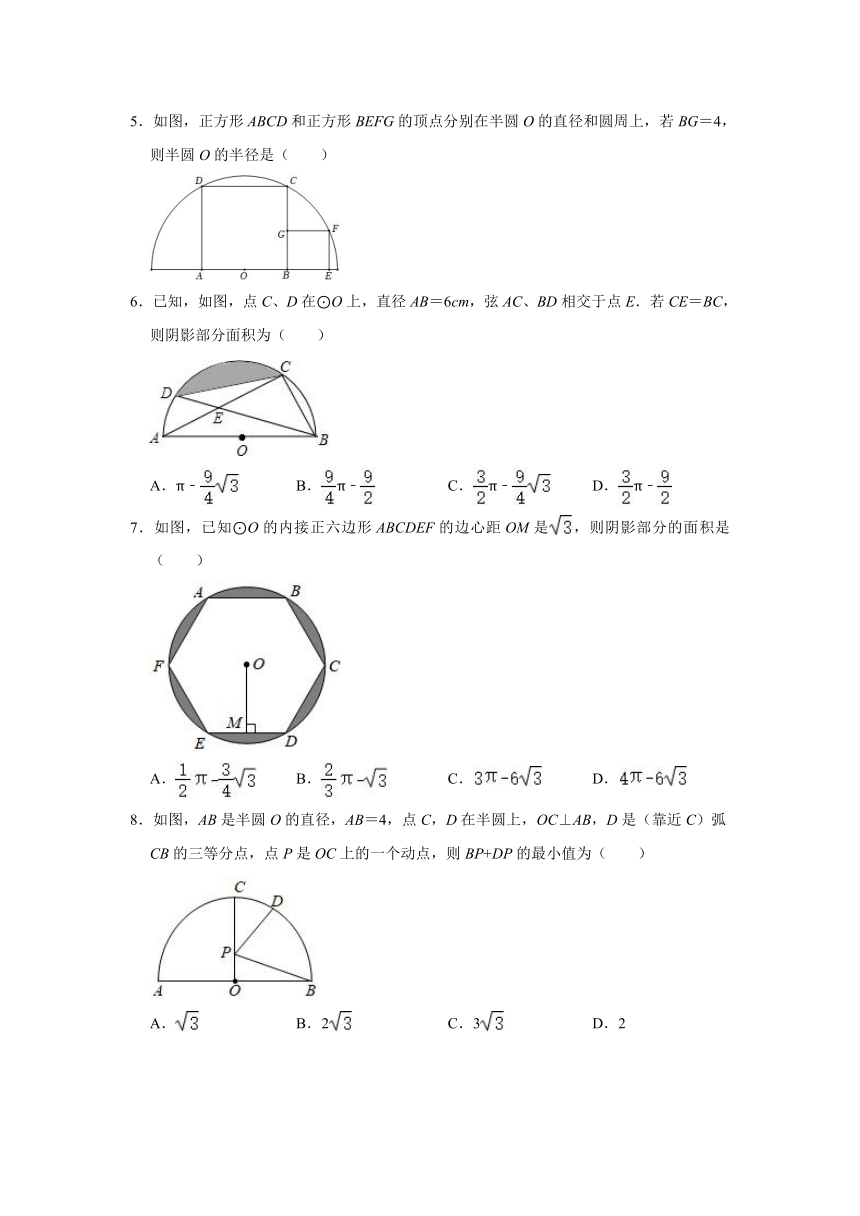
1.如图,⊙O的直径AB=12,弦CD垂直AB于点P.若BP=2,则CD的长为( )
A.2 B.4 C.4 D.8
2.如图,AB是⊙O的直径,点D是弧AC的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AE=2,⊙O的直径为10,则AC长为( )
A.5 B.6 C.7 D.8
3.如图,点A、B、C、D在⊙O上,,∠CAD=30°,∠ACD=50°,则∠ADB=( )
A.30° B.50° C.70° D.80°
4.如图,在直角坐标系中,点A(0,3)、点B(4,3)、点C(0,﹣1),则△ABC外接圆的半径为( )
A.2 B.3 C.4 D.
5.如图,正方形ABCD和正方形BEFG的顶点分别在半圆O的直径和圆周上,若BG=4,则半圆O的半径是( )
6.已知,如图,点C、D在⊙O上,直径AB=6cm,弦AC、BD相交于点E.若CE=BC,则阴影部分面积为( )
A.π﹣ B.π﹣ C.π﹣ D.π﹣
7.如图,已知⊙O的内接正六边形ABCDEF的边心距OM是,则阴影部分的面积是( )
A. B. C. D.
8.如图,AB是半圆O的直径,AB=4,点C,D在半圆上,OC⊥AB,D是(靠近C)弧CB的三等分点,点P是OC上的一个动点,则BP+DP的最小值为( )
A. B.2 C.3 D.2
二.填空题(共8小题,满分40分)
9.如图,点A,点B,点C在⊙O上,分别连接AB,BC,OC.若AB=BC,∠B=40°,则∠OCB= .
10.如图,已知弦AB是⊙O的直径,且AB=10,点C为圆上一点,满足AC=6,AD平分∠BAC且交⊙O于点D,连接BC、OD交于点E,连接BD,则ED= ;AD= .
11.如图,在每个小正方形的边长均为1的网格图中,一段圆弧经过格点A,B,C,格点A,D的连线交圆弧于点E,则图中阴影部分面积为 .
12.如图所示,以 ABCD的顶点A为圆心,AB为半径作圆,交AD,BC于E,F两点,延长BA交⊙A于点G,连接GF,FE,当∠D=50°时,∠GFE= °.
13.如图,AD是正五边形ABCDE的一条对角线,以C为圆心,CB为半径画弧交AD于点F,连接CF,则∠CFD= °.
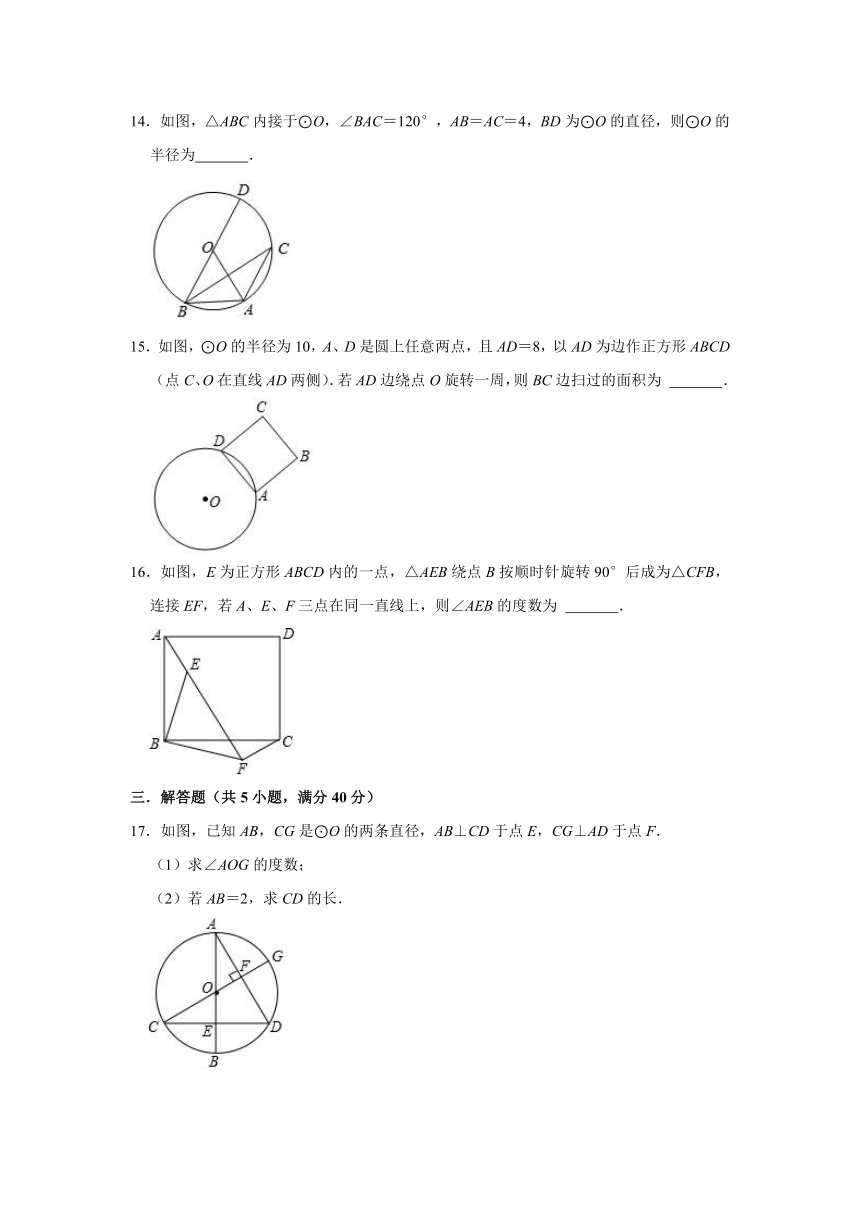
14.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4,BD为⊙O的直径,则⊙O的半径为 .
15.如图,⊙O的半径为10,A、D是圆上任意两点,且AD=8,以AD为边作正方形ABCD(点C、O在直线AD两侧).若AD边绕点O旋转一周,则BC边扫过的面积为 .
16.如图,E为正方形ABCD内的一点,△AEB绕点B按顺时针旋转90°后成为△CFB,连接EF,若A、E、F三点在同一直线上,则∠AEB的度数为 .
三.解答题(共5小题,满分40分)
17.如图,已知AB,CG是⊙O的两条直径,AB⊥CD于点E,CG⊥AD于点F.
(1)求∠AOG的度数;
(2)若AB=2,求CD的长.
18.如图,AB、AC是⊙O的两条弦,且AB=AC,点D是的中点,连接并延长BD、CD,分别交AC、AB的延长线于点E、F.
(1)求证:DF=DE;
(2)若BD=6,CE=8,求⊙O的半径.
19.如图,在△ABC中,E是BC边上的点,以AE为直径的⊙O与AB,BC,AC分别交于点F,D,G,且D是的中点.
(1)求证AB=AC;
(2)连接DF,当DF∥AC时,若AB=10,BC=12,求CE的长.
20.如图所示,某地有一座圆弧形的拱桥,桥下的水面宽度AB为7.2m,拱顶高出水面(CD)2.4m,现有一艘宽EF为3m且船舱顶部为长方形并高出水面1.5m的货船要经过这里,则货船能顺利通过这座拱桥吗?请作出判断并说明理由.
21.如图,AB为⊙O直径,点D为AB下方⊙O上一点,点C为弧ABD中点,连接CD,CA.
(1)求证:∠ABD=2∠BDC;
(2)过点C作CE⊥AB于H,交AD于E,求证:EA=EC;
(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长
参考答案
一.选择题(共8小题,满分40分)
1.解:如图,连接OC,
∵AB=12,
∴OC=OB=6,
∵PB=2,
∴OP=4,
在Rt△OPC中,CP=,
∵CD⊥AB,
∴CP=DP,
∴CD=2PC=.
故选:C.
2.解:连接OF,如图:
∵DE⊥AB,AB过圆心O,
∴DE=EF,=,
∵D为弧AC的中点,
∴=,
∴=,
∴AC=DF,
∵⊙O的直径为10,
∴OF=OA=5,
∵AE=2,
∴OE=OA﹣AE=5﹣2=3,
在Rt△OEF中,由勾股定理得:EF===4,
∴DE=EF=4,
∴AC=DF=DE+EF=4+4=8,
故选:D.
3.解:∵,∠CAD=30°,
∴∠CAD=∠CAB=30°,
∴∠DBC=∠DAC=30°,
∵∠ACD=50°,
∴∠ABD=50°,
∴∠ACB=∠ADB=180°﹣∠CAB﹣∠ABC=180°﹣50°﹣30°﹣30°=70°.
故选:C.
4.解:连接AB、BC,如图,
∵A(0,3)、B(4,3),
∴AB⊥y轴,
∴∠BAC=90°,
∴BC为△ABC外接圆的直径,
∵AC=3+1=4,AB=4,
∴BC==4,
∴△ABC外接圆的半径为2.
故选:D.
5.解:连接OC,OF,
设OB=x,
∵四边形ABCD是正方形且顶点D和C在圆上,
∴AB=BC=2x,∠OBC=90°,
∵BG=4,四边形BEFG是正方形,
∴OE=x+4,EF=BE=BG=4,∠FEB=90°,
在Rt△BCO中,OC=,
在Rt△FEO中,OF=,
∵OF=OC,
∴5x2=x2+8x+32,
解得x=4或x=﹣2(舍去)
当x=4时,OC=4,
则半圆O的半径是4.
故选:C.
6.解:连接OD、OC,
∵AB是直径,
∴∠ACB=90°,
∵CE=BC,
∴∠DBC=∠CEB=45°,
∴的度数为90°,
∴∠DOC=90°,
∴S阴影=S扇形﹣S△ODC=﹣×3×3=﹣.
故选:B.
7.解:如图所示,连接OA、OB,
∵多边形ABCDEF是正六边形,
∴∠AOB=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴∠OAM=60°,
∴OA=2,
∴AB=2,
∴==.
∴阴影部分的面积:π×22﹣6=4π﹣6.
故选:D.
8.解:如图,连接AD,PA,OD,DB.
∵OC⊥AB,OA=OB,
∴PA=PB,∠COB=90°,
∵=2,
∴∠DOB=×90°=60°,
∵OD=OB,
∴△OBD是等边三角形,
∴∠ABD=60°
∵AB是直径,
∴∠ADB=90°,
∴AD=2,
∵PB+PD=PA+PD≥AD,
∴PD+PB≥2,
∴PD+PB的最小值为2,
故选:B.
二.填空题(共8小题,满分40分)
9.解:如图,连接AO,BO,
∴OA=OB=OC,
∴∠OBC=∠OCB,∠OAB=∠OBA,
∵AB=BC,
∴∠BOC=∠AOB,
∴∠OBA=(180°﹣∠AOB)=(180°﹣∠BOC)=∠OBC,
∵∠ABC=40°,OB=OC,
∴∠OCB=∠OBC=20°.
故答案为:20°.
10.解:∵弦AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
在Rt△ABC中,BC===8,
∵AD平分∠BAC,
∴∠CAD=∠BAD,
∴=,
∴OD⊥BC,
∴BE=CE=4,
∴OE=AC=3,
∴DE=OD﹣OE=5﹣3=2,
在Rt△BDE中,BD==2,
在Rt△ADB中,AD==4.
故答案为2,4.
11.解:如图,作AB、BC的垂直平分线,两线交于O,连接OA、OE、OC,
由图形可知△ACD是等腰直角三角形,
∴∠DAC=45°,
∴∠EOC=90°,
∵AC=CD==,
∴OA=OE=,
∴S阴影=S△ACD﹣S△AOE﹣S扇形EOC=×﹣×﹣=﹣π.
故答案为:﹣π.
12.解:∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠GAD=∠D=50°,
∴∠GFE=∠GAE=×50°=25°.
故答案为25.
13.解:∵五边形ABCDE是正五边形,
∴∠CDE=∠E==108°,AE=DE,
∴∠EDA=∠EAD=(180°﹣∠E)=36°,
∴∠CDF=∠CDE﹣∠EDA=108°﹣36°=72°,
∵CF=CD,
∴∠CFD=∠CDF=72°,
故答案为:72.
14.解:连接AD,
∵∠BAC=120°,AB=AC=4,
∴∠C=∠ABC=(180°﹣∠BAC)=30°,
∴∠D=∠C=30°,
∵BD是直径,
∴∠BAD=90°
∴BD=2AB=8,
∴⊙O的半径为4,
故答案为:4.
15.解:如图所示,连接OD、OC,过点O作OE⊥AD于点E,延长OE交BC于点F.
∵AD为弦,OE⊥AD,
由垂径定理可得DE=AE==4.
∵四边形ABCD为正方形,
∴BC∥AD,AD=BC=8,
∴∠CFO=∠DEO=90°,
∴四边形DEFC为矩形,CF=DE=4.
∵AD边绕点O旋转一周,则BC边扫过的图形为以OC为外圆半径,
OF为内圆半径的圆环,
∴圆环面积为S=π OC2﹣π OF2=π(OC2﹣OF2)=π CF2=16π.
故答案为:16π.
16.解:由旋转可知,
BE=BF,∠EBF=90°,
∴△BEF是等腰直角三角形,
∴∠BEF=45°,
∵A、E、F三点在同一直线上
∴∠AEB=180°﹣45°=135°,
故答案为:135°.
三.解答题(共5小题,满分40分)
17.解:(1)连接OD,
∵AB⊥CD,
∴=,
∴∠BOC=∠BOD,
由圆周角定理得,∠A=∠BOD,
∴∠A=∠BOD,
∵∠AOG=∠BOD,
∴∠A=∠AOG,
∵∠OFA=90°,
∴∠AOG=60°;
(2)∵∠AOG=60°,
∴∠COE=60°,
∴∠C=30°,
∴OE=OC=,
∴CE==,
∵AB⊥CD,
∴CD=2CE=.
18.(1)证明:连接AD,
∵点D是的中点,
∴∠CAD=∠BAD,
∴CD=BD,
在△CAD和△BAD中,
,
∴△CAD≌△BAD(SAS),
∴∠ACD=∠ABD,
∴∠DCE=∠DBF,
在△CED和△BFD中,
,
∴△CED≌△BFD(ASA),
∴DF=DE;
(2)解:∵四边形ABDC是圆内接四边形,
∴∠DBF=∠ACD,
∵∠ACD=∠ABD,
∴∠ABD=∠DBF,
∴∠ABD=90°,
∴∠ECD=∠ABD=90°,
∴AD是⊙O的直径,
∵CD=BD=6,CE=8,
∴DE==10,
∴EB=10+6=16,
在Rt△ABE中,AB2+BE2=AE2,
设AB=AC=x,则x2+162=(x+8)2,
解得x=12,
∴AB=12,
在Rt△ABD中,AB2+BD2=AD2,
∴AD==6,
∴⊙O的半径为3.
19.(1)证明:连接AD,
∵AE是⊙O的直径,
∴∠EDA=90°,
∵D是的中点,
∴=,
∴∠BAD=∠CAD,
∵∠B+∠BAD=90°,∠C+∠CAD=90°,
∴∠B=∠C,
∴AB=AC;
(2)解:连接DF,DG.
∵AB=AC,AD⊥BC,
∴BD=CD,
∵AB=10,BC=12,
∴AC=10,CD=6,
由勾股定理得:AD==8,
∵DF∥AC,
∴=,
∴BF=FA,
在Rt△ADB中,AB=10,BF=FA,
∴DG=DF=AB=5,
∴DG=DF=5,
∵∠C=∠C,∠CDG=∠CAE,
∴=,即=,
解得:AE=,
在Rt△ADE中,∠ADE=90°,AE=,AD=8,
∴DE==,
∴EC=CD﹣DE=.
20.解:货船能顺利通过这座拱桥,理由如下:
如图,连接ON、OA.
∵OC⊥AB,AB=7.2m,
∴AD=AB=3.6(m),
设OB=OC=ON=rm,则OD=(r﹣2.4)m,
在Rt△AOD中,根据勾股定理得:r2=(r﹣2.4)2+3.62,
解得:r=3.9.
∵CD=2.4m,船舱顶部为正方形并高出水面1.5m,
∴CH=2.4﹣1.5=0.9(m),
∴OH=3.9﹣0.9=3(m),
在Rt△OHN中,HN2=ON2﹣OH2=3.92﹣32=6.21(m2),
∴HN=(m),
∴MN=2HN=2(m)>3m,
∴货船能顺利通过这座拱桥.
21.解:(1)如图1,设∠BDC=α,∠DAC=β,
则∠CAB=∠BDC=α,
∵点C为弧ABD中点,
∴=,
∴∠ADC=∠DAC=β,
∴∠DAB=β﹣α,
连接AD,
∵AB为⊙O直径,
∴∠ADB=90°,
∴α+β=90°,
∴β=90°﹣α,
∴∠ABD=90°﹣∠DAB=90°﹣(β﹣α),
∴∠ABD=2α,
∴∠ABD=2∠BDC;
(2)∵CE⊥AB,
∴∠ACE+∠CAB=∠ADC+∠BDC=90°,
∵∠CAB=∠CDB,
∴∠ACE=∠ADC,
∵∠CAE=∠ADC,
∴∠ACE=∠CAE,
∴AE=CE;
(3)如图2,连接OC,
∴∠COB=2∠CAB,
∵∠ABD=2∠BDC,∠BDC=∠CAB,
∴∠COB=∠ABD,
∵∠OHC=∠ADB=90°,
∴,
∵OH=5,
∴BD=10,
∴AB==26,
∴AO=13,
∴AH=18,
∴,即=,
∴AE=,
∴DE=.
一.选择题(共8小题,满分40分)
1.如图,⊙O的直径AB=12,弦CD垂直AB于点P.若BP=2,则CD的长为( )
A.2 B.4 C.4 D.8
2.如图,AB是⊙O的直径,点D是弧AC的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AE=2,⊙O的直径为10,则AC长为( )
A.5 B.6 C.7 D.8
3.如图,点A、B、C、D在⊙O上,,∠CAD=30°,∠ACD=50°,则∠ADB=( )
A.30° B.50° C.70° D.80°
4.如图,在直角坐标系中,点A(0,3)、点B(4,3)、点C(0,﹣1),则△ABC外接圆的半径为( )
A.2 B.3 C.4 D.
5.如图,正方形ABCD和正方形BEFG的顶点分别在半圆O的直径和圆周上,若BG=4,则半圆O的半径是( )
6.已知,如图,点C、D在⊙O上,直径AB=6cm,弦AC、BD相交于点E.若CE=BC,则阴影部分面积为( )
A.π﹣ B.π﹣ C.π﹣ D.π﹣
7.如图,已知⊙O的内接正六边形ABCDEF的边心距OM是,则阴影部分的面积是( )
A. B. C. D.
8.如图,AB是半圆O的直径,AB=4,点C,D在半圆上,OC⊥AB,D是(靠近C)弧CB的三等分点,点P是OC上的一个动点,则BP+DP的最小值为( )
A. B.2 C.3 D.2
二.填空题(共8小题,满分40分)
9.如图,点A,点B,点C在⊙O上,分别连接AB,BC,OC.若AB=BC,∠B=40°,则∠OCB= .
10.如图,已知弦AB是⊙O的直径,且AB=10,点C为圆上一点,满足AC=6,AD平分∠BAC且交⊙O于点D,连接BC、OD交于点E,连接BD,则ED= ;AD= .
11.如图,在每个小正方形的边长均为1的网格图中,一段圆弧经过格点A,B,C,格点A,D的连线交圆弧于点E,则图中阴影部分面积为 .
12.如图所示,以 ABCD的顶点A为圆心,AB为半径作圆,交AD,BC于E,F两点,延长BA交⊙A于点G,连接GF,FE,当∠D=50°时,∠GFE= °.
13.如图,AD是正五边形ABCDE的一条对角线,以C为圆心,CB为半径画弧交AD于点F,连接CF,则∠CFD= °.
14.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4,BD为⊙O的直径,则⊙O的半径为 .
15.如图,⊙O的半径为10,A、D是圆上任意两点,且AD=8,以AD为边作正方形ABCD(点C、O在直线AD两侧).若AD边绕点O旋转一周,则BC边扫过的面积为 .
16.如图,E为正方形ABCD内的一点,△AEB绕点B按顺时针旋转90°后成为△CFB,连接EF,若A、E、F三点在同一直线上,则∠AEB的度数为 .
三.解答题(共5小题,满分40分)
17.如图,已知AB,CG是⊙O的两条直径,AB⊥CD于点E,CG⊥AD于点F.
(1)求∠AOG的度数;
(2)若AB=2,求CD的长.
18.如图,AB、AC是⊙O的两条弦,且AB=AC,点D是的中点,连接并延长BD、CD,分别交AC、AB的延长线于点E、F.
(1)求证:DF=DE;
(2)若BD=6,CE=8,求⊙O的半径.
19.如图,在△ABC中,E是BC边上的点,以AE为直径的⊙O与AB,BC,AC分别交于点F,D,G,且D是的中点.
(1)求证AB=AC;
(2)连接DF,当DF∥AC时,若AB=10,BC=12,求CE的长.
20.如图所示,某地有一座圆弧形的拱桥,桥下的水面宽度AB为7.2m,拱顶高出水面(CD)2.4m,现有一艘宽EF为3m且船舱顶部为长方形并高出水面1.5m的货船要经过这里,则货船能顺利通过这座拱桥吗?请作出判断并说明理由.
21.如图,AB为⊙O直径,点D为AB下方⊙O上一点,点C为弧ABD中点,连接CD,CA.
(1)求证:∠ABD=2∠BDC;
(2)过点C作CE⊥AB于H,交AD于E,求证:EA=EC;
(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长
参考答案
一.选择题(共8小题,满分40分)
1.解:如图,连接OC,
∵AB=12,
∴OC=OB=6,
∵PB=2,
∴OP=4,
在Rt△OPC中,CP=,
∵CD⊥AB,
∴CP=DP,
∴CD=2PC=.
故选:C.
2.解:连接OF,如图:
∵DE⊥AB,AB过圆心O,
∴DE=EF,=,
∵D为弧AC的中点,
∴=,
∴=,
∴AC=DF,
∵⊙O的直径为10,
∴OF=OA=5,
∵AE=2,
∴OE=OA﹣AE=5﹣2=3,
在Rt△OEF中,由勾股定理得:EF===4,
∴DE=EF=4,
∴AC=DF=DE+EF=4+4=8,
故选:D.
3.解:∵,∠CAD=30°,
∴∠CAD=∠CAB=30°,
∴∠DBC=∠DAC=30°,
∵∠ACD=50°,
∴∠ABD=50°,
∴∠ACB=∠ADB=180°﹣∠CAB﹣∠ABC=180°﹣50°﹣30°﹣30°=70°.
故选:C.
4.解:连接AB、BC,如图,
∵A(0,3)、B(4,3),
∴AB⊥y轴,
∴∠BAC=90°,
∴BC为△ABC外接圆的直径,
∵AC=3+1=4,AB=4,
∴BC==4,
∴△ABC外接圆的半径为2.
故选:D.
5.解:连接OC,OF,
设OB=x,
∵四边形ABCD是正方形且顶点D和C在圆上,
∴AB=BC=2x,∠OBC=90°,
∵BG=4,四边形BEFG是正方形,
∴OE=x+4,EF=BE=BG=4,∠FEB=90°,
在Rt△BCO中,OC=,
在Rt△FEO中,OF=,
∵OF=OC,
∴5x2=x2+8x+32,
解得x=4或x=﹣2(舍去)
当x=4时,OC=4,
则半圆O的半径是4.
故选:C.
6.解:连接OD、OC,
∵AB是直径,
∴∠ACB=90°,
∵CE=BC,
∴∠DBC=∠CEB=45°,
∴的度数为90°,
∴∠DOC=90°,
∴S阴影=S扇形﹣S△ODC=﹣×3×3=﹣.
故选:B.
7.解:如图所示,连接OA、OB,
∵多边形ABCDEF是正六边形,
∴∠AOB=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴∠OAM=60°,
∴OA=2,
∴AB=2,
∴==.
∴阴影部分的面积:π×22﹣6=4π﹣6.
故选:D.
8.解:如图,连接AD,PA,OD,DB.
∵OC⊥AB,OA=OB,
∴PA=PB,∠COB=90°,
∵=2,
∴∠DOB=×90°=60°,
∵OD=OB,
∴△OBD是等边三角形,
∴∠ABD=60°
∵AB是直径,
∴∠ADB=90°,
∴AD=2,
∵PB+PD=PA+PD≥AD,
∴PD+PB≥2,
∴PD+PB的最小值为2,
故选:B.
二.填空题(共8小题,满分40分)
9.解:如图,连接AO,BO,
∴OA=OB=OC,
∴∠OBC=∠OCB,∠OAB=∠OBA,
∵AB=BC,
∴∠BOC=∠AOB,
∴∠OBA=(180°﹣∠AOB)=(180°﹣∠BOC)=∠OBC,
∵∠ABC=40°,OB=OC,
∴∠OCB=∠OBC=20°.
故答案为:20°.
10.解:∵弦AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
在Rt△ABC中,BC===8,
∵AD平分∠BAC,
∴∠CAD=∠BAD,
∴=,
∴OD⊥BC,
∴BE=CE=4,
∴OE=AC=3,
∴DE=OD﹣OE=5﹣3=2,
在Rt△BDE中,BD==2,
在Rt△ADB中,AD==4.
故答案为2,4.
11.解:如图,作AB、BC的垂直平分线,两线交于O,连接OA、OE、OC,
由图形可知△ACD是等腰直角三角形,
∴∠DAC=45°,
∴∠EOC=90°,
∵AC=CD==,
∴OA=OE=,
∴S阴影=S△ACD﹣S△AOE﹣S扇形EOC=×﹣×﹣=﹣π.
故答案为:﹣π.
12.解:∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠GAD=∠D=50°,
∴∠GFE=∠GAE=×50°=25°.
故答案为25.
13.解:∵五边形ABCDE是正五边形,
∴∠CDE=∠E==108°,AE=DE,
∴∠EDA=∠EAD=(180°﹣∠E)=36°,
∴∠CDF=∠CDE﹣∠EDA=108°﹣36°=72°,
∵CF=CD,
∴∠CFD=∠CDF=72°,
故答案为:72.
14.解:连接AD,
∵∠BAC=120°,AB=AC=4,
∴∠C=∠ABC=(180°﹣∠BAC)=30°,
∴∠D=∠C=30°,
∵BD是直径,
∴∠BAD=90°
∴BD=2AB=8,
∴⊙O的半径为4,
故答案为:4.
15.解:如图所示,连接OD、OC,过点O作OE⊥AD于点E,延长OE交BC于点F.
∵AD为弦,OE⊥AD,
由垂径定理可得DE=AE==4.
∵四边形ABCD为正方形,
∴BC∥AD,AD=BC=8,
∴∠CFO=∠DEO=90°,
∴四边形DEFC为矩形,CF=DE=4.
∵AD边绕点O旋转一周,则BC边扫过的图形为以OC为外圆半径,
OF为内圆半径的圆环,
∴圆环面积为S=π OC2﹣π OF2=π(OC2﹣OF2)=π CF2=16π.
故答案为:16π.
16.解:由旋转可知,
BE=BF,∠EBF=90°,
∴△BEF是等腰直角三角形,
∴∠BEF=45°,
∵A、E、F三点在同一直线上
∴∠AEB=180°﹣45°=135°,
故答案为:135°.
三.解答题(共5小题,满分40分)
17.解:(1)连接OD,
∵AB⊥CD,
∴=,
∴∠BOC=∠BOD,
由圆周角定理得,∠A=∠BOD,
∴∠A=∠BOD,
∵∠AOG=∠BOD,
∴∠A=∠AOG,
∵∠OFA=90°,
∴∠AOG=60°;
(2)∵∠AOG=60°,
∴∠COE=60°,
∴∠C=30°,
∴OE=OC=,
∴CE==,
∵AB⊥CD,
∴CD=2CE=.
18.(1)证明:连接AD,
∵点D是的中点,
∴∠CAD=∠BAD,
∴CD=BD,
在△CAD和△BAD中,
,
∴△CAD≌△BAD(SAS),
∴∠ACD=∠ABD,
∴∠DCE=∠DBF,
在△CED和△BFD中,
,
∴△CED≌△BFD(ASA),
∴DF=DE;
(2)解:∵四边形ABDC是圆内接四边形,
∴∠DBF=∠ACD,
∵∠ACD=∠ABD,
∴∠ABD=∠DBF,
∴∠ABD=90°,
∴∠ECD=∠ABD=90°,
∴AD是⊙O的直径,
∵CD=BD=6,CE=8,
∴DE==10,
∴EB=10+6=16,
在Rt△ABE中,AB2+BE2=AE2,
设AB=AC=x,则x2+162=(x+8)2,
解得x=12,
∴AB=12,
在Rt△ABD中,AB2+BD2=AD2,
∴AD==6,
∴⊙O的半径为3.
19.(1)证明:连接AD,
∵AE是⊙O的直径,
∴∠EDA=90°,
∵D是的中点,
∴=,
∴∠BAD=∠CAD,
∵∠B+∠BAD=90°,∠C+∠CAD=90°,
∴∠B=∠C,
∴AB=AC;
(2)解:连接DF,DG.
∵AB=AC,AD⊥BC,
∴BD=CD,
∵AB=10,BC=12,
∴AC=10,CD=6,
由勾股定理得:AD==8,
∵DF∥AC,
∴=,
∴BF=FA,
在Rt△ADB中,AB=10,BF=FA,
∴DG=DF=AB=5,
∴DG=DF=5,
∵∠C=∠C,∠CDG=∠CAE,
∴=,即=,
解得:AE=,
在Rt△ADE中,∠ADE=90°,AE=,AD=8,
∴DE==,
∴EC=CD﹣DE=.
20.解:货船能顺利通过这座拱桥,理由如下:
如图,连接ON、OA.
∵OC⊥AB,AB=7.2m,
∴AD=AB=3.6(m),
设OB=OC=ON=rm,则OD=(r﹣2.4)m,
在Rt△AOD中,根据勾股定理得:r2=(r﹣2.4)2+3.62,
解得:r=3.9.
∵CD=2.4m,船舱顶部为正方形并高出水面1.5m,
∴CH=2.4﹣1.5=0.9(m),
∴OH=3.9﹣0.9=3(m),
在Rt△OHN中,HN2=ON2﹣OH2=3.92﹣32=6.21(m2),
∴HN=(m),
∴MN=2HN=2(m)>3m,
∴货船能顺利通过这座拱桥.
21.解:(1)如图1,设∠BDC=α,∠DAC=β,
则∠CAB=∠BDC=α,
∵点C为弧ABD中点,
∴=,
∴∠ADC=∠DAC=β,
∴∠DAB=β﹣α,
连接AD,
∵AB为⊙O直径,
∴∠ADB=90°,
∴α+β=90°,
∴β=90°﹣α,
∴∠ABD=90°﹣∠DAB=90°﹣(β﹣α),
∴∠ABD=2α,
∴∠ABD=2∠BDC;
(2)∵CE⊥AB,
∴∠ACE+∠CAB=∠ADC+∠BDC=90°,
∵∠CAB=∠CDB,
∴∠ACE=∠ADC,
∵∠CAE=∠ADC,
∴∠ACE=∠CAE,
∴AE=CE;
(3)如图2,连接OC,
∴∠COB=2∠CAB,
∵∠ABD=2∠BDC,∠BDC=∠CAB,
∴∠COB=∠ABD,
∵∠OHC=∠ADB=90°,
∴,
∵OH=5,
∴BD=10,
∴AB==26,
∴AO=13,
∴AH=18,
∴,即=,
∴AE=,
∴DE=.
同课章节目录
