浙教版八年级数学上册 2.7探索勾股定理 自主提升训练 (含解析)
文档属性
| 名称 | 浙教版八年级数学上册 2.7探索勾股定理 自主提升训练 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 306.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 06:57:49 | ||
图片预览

文档简介
2022-2023学年浙教版八年级数学上册《2.7探索勾股定理》自主提升训练(附答案)
一.选择题
1.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A.3cm2 B.4cm2 C.6cm2 D.12cm2
2.△ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是( )
A.4.8 B.4.8或3.8 C.3.8 D.5
3.直角三角形的两条直角边为a、b,斜边为c,斜边上的高为h,下列结论:①a2+b2=c2;②ab=ch;③.其中正确的是( )
A.① B.①②③ C.①② D.①③
4.如图所示,在△ABC中,AB=AC=5,BC=8,CD是AB边上的高,则线段AD的长度为( )
A. B. C. D.
5.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形的面积为64,小正方形的面积为9,若用x、y分别表示直角三角形的两直角边长(x>y),则下列四个说法:①x2+y2=64:②x﹣y=3;③2xy=55;④x+y=11.其中正确的是( )
A.①② B.①②③ C.①②④ D.①②③④
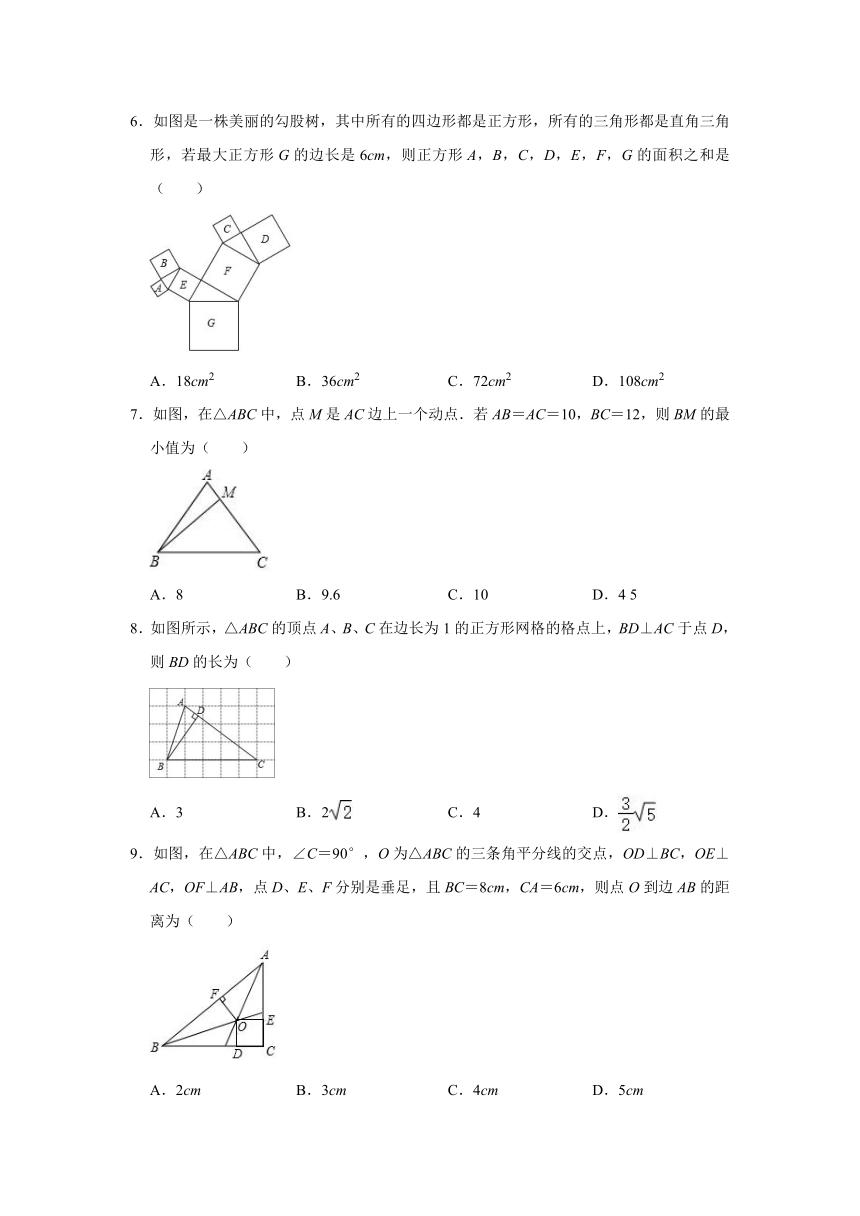
6.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若最大正方形G的边长是6cm,则正方形A,B,C,D,E,F,G的面积之和是( )
A.18cm2 B.36cm2 C.72cm2 D.108cm2
7.如图,在△ABC中,点M是AC边上一个动点.若AB=AC=10,BC=12,则BM的最小值为( )
A.8 B.9.6 C.10 D.4 5
8.如图所示,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为( )
A.3 B.2 C.4 D.
9.如图,在△ABC中,∠C=90°,O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且BC=8cm,CA=6cm,则点O到边AB的距离为( )
A.2cm B.3cm C.4cm D.5cm
二.填空题
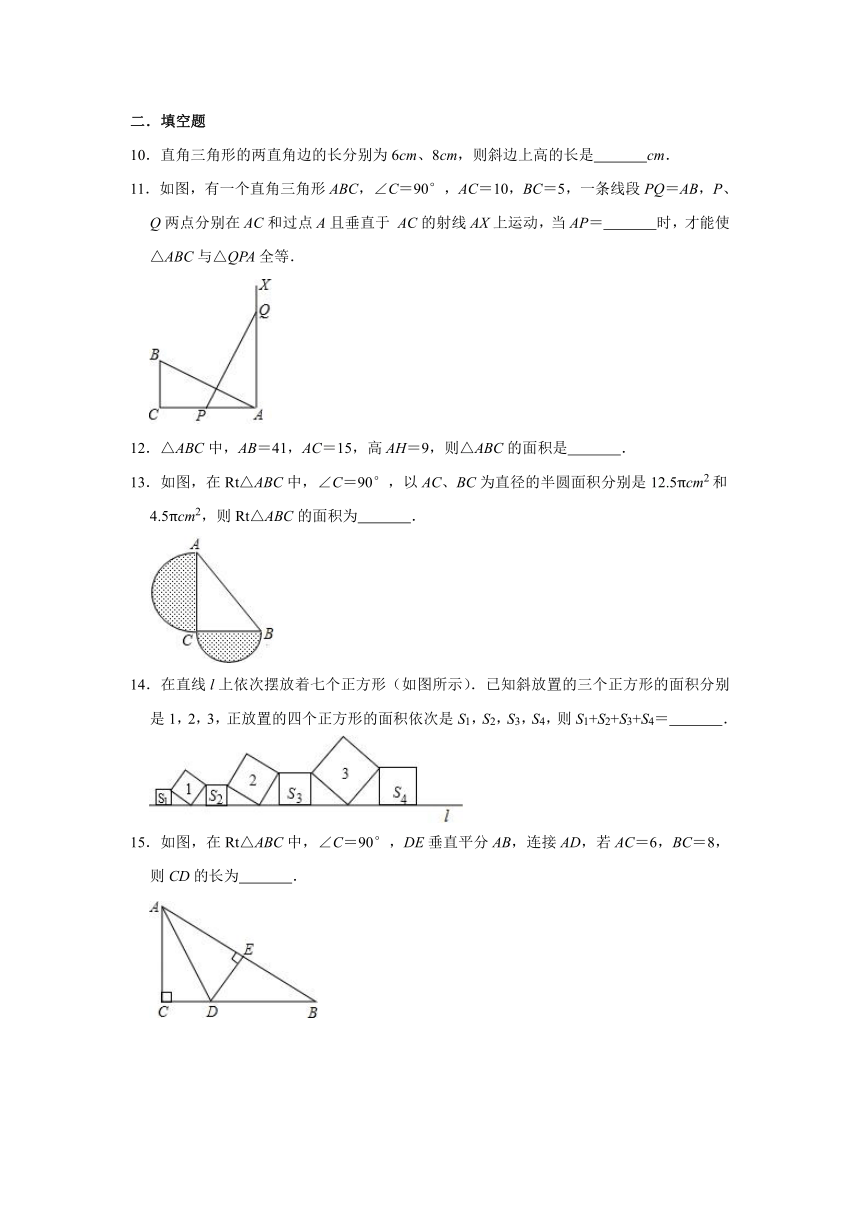
10.直角三角形的两直角边的长分别为6cm、8cm,则斜边上高的长是 cm.
11.如图,有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于 AC的射线AX上运动,当AP= 时,才能使△ABC与△QPA全等.
12.△ABC中,AB=41,AC=15,高AH=9,则△ABC的面积是 .
13.如图,在Rt△ABC中,∠C=90°,以AC、BC为直径的半圆面积分别是12.5πcm2和4.5πcm2,则Rt△ABC的面积为 .
14.在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1,S2,S3,S4,则S1+S2+S3+S4= .
15.如图,在Rt△ABC中,∠C=90°,DE垂直平分AB,连接AD,若AC=6,BC=8,则CD的长为 .
三.解答题
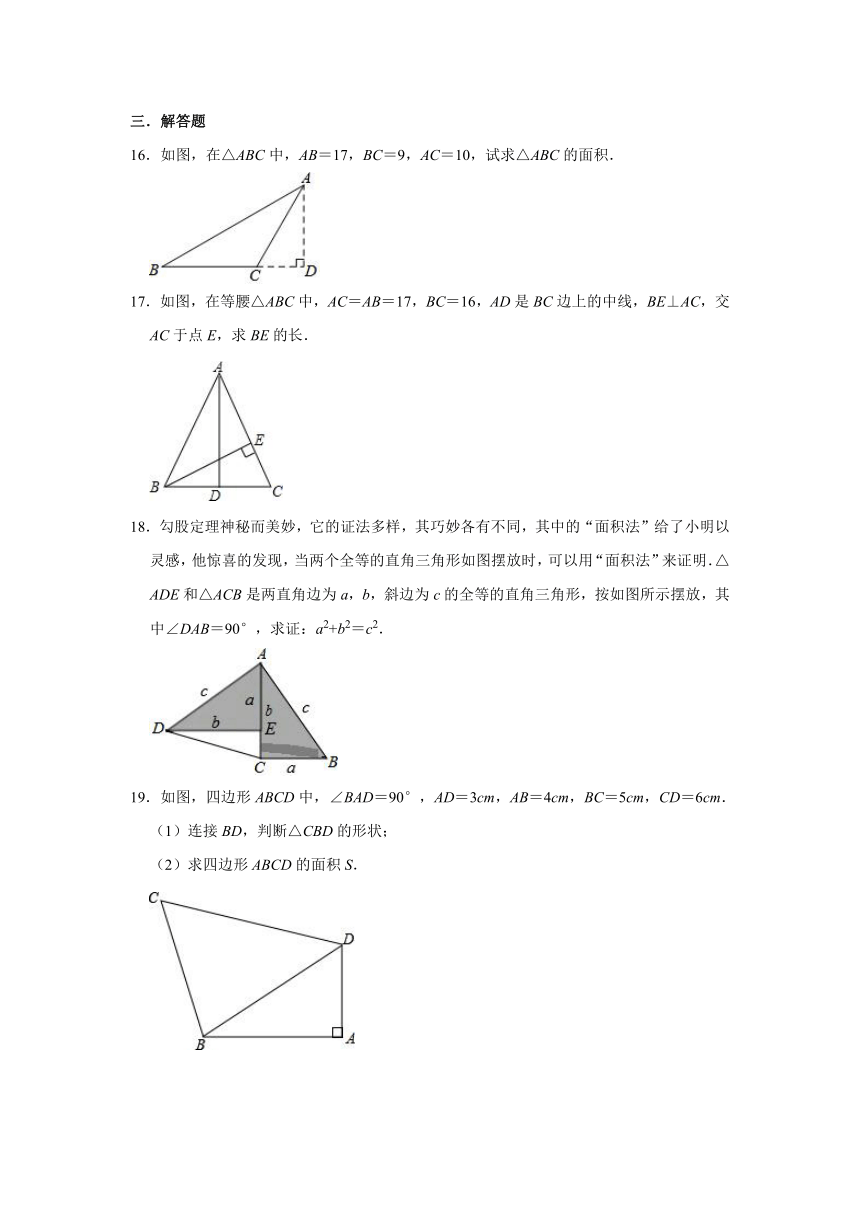
16.如图,在△ABC中,AB=17,BC=9,AC=10,试求△ABC的面积.
17.如图,在等腰△ABC中,AC=AB=17,BC=16,AD是BC边上的中线,BE⊥AC,交AC于点E,求BE的长.
18.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明以灵感,他惊喜的发现,当两个全等的直角三角形如图摆放时,可以用“面积法”来证明.△ADE和△ACB是两直角边为a,b,斜边为c的全等的直角三角形,按如图所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
19.如图,四边形ABCD中,∠BAD=90°,AD=3cm,AB=4cm,BC=5cm,CD=6cm.
(1)连接BD,判断△CBD的形状;
(2)求四边形ABCD的面积S.
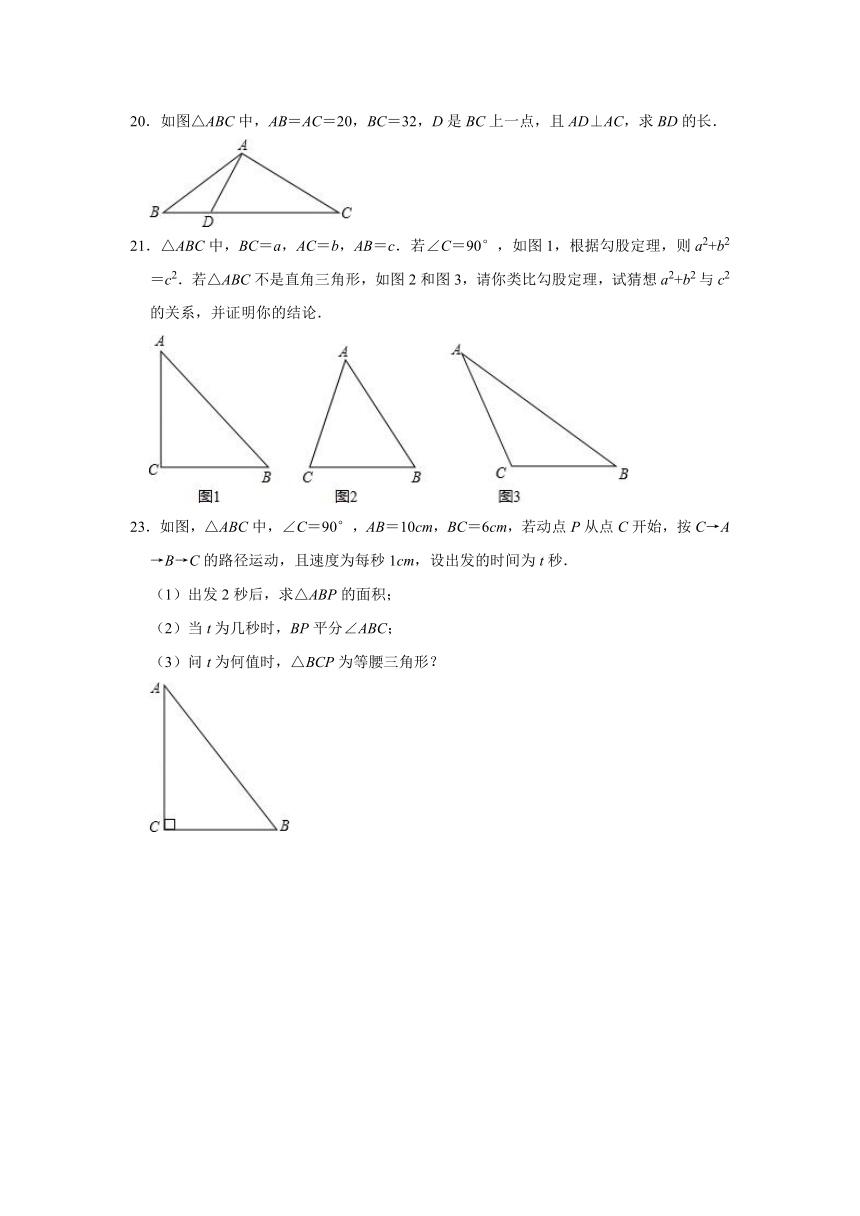
20.如图△ABC中,AB=AC=20,BC=32,D是BC上一点,且AD⊥AC,求BD的长.
21.△ABC中,BC=a,AC=b,AB=c.若∠C=90°,如图1,根据勾股定理,则a2+b2=c2.若△ABC不是直角三角形,如图2和图3,请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.
23.如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的面积;
(2)当t为几秒时,BP平分∠ABC;
(3)问t为何值时,△BCP为等腰三角形?
参考答案
一.选择题
1.解:将此长方形折叠,使点B与点D重合,∴BE=ED.
∵AD=9cm=AE+DE=AE+BE.
∴BE=9﹣AE,
根据勾股定理可知AB2+AE2=BE2.
解得AE=4.
∴△ABE的面积为3×4÷2=6.故选:C.
2.解:过A点作AF⊥BC于F,连接AP,
∵△ABC中,AB=AC=5,BC=8,
∴BF=4,
∴△ABF中,AF==3,
∴×8×3=×5×PD+×5×PE,
12=×5×(PD+PE)
PD+PE=4.8.
故选:A.
3.解:∵直角三角形的两条直角边为a、b,斜边为c,斜边上的高为h,
∴由勾股定理可知:a2+b2=c2,①正确;
这个直角三角形的面积=ab=ch,
∴ab=ch,②正确;
∴a2b2=c2h2,
∴====,③正确.
故选:B.
4.解:设AD=x
∵CD⊥AB,
∴∠D=90°,
∴CD2=BC2﹣BD2=AC2﹣AD2,
∴82﹣(5+x)2=52﹣x2,
∴x=,
∴AD=,
故选:D.
5.解:①∵△ABC为直角三角形,
∴根据勾股定理:x2+y2=AB2=64,
故本选项正确;
②由图可知,x﹣y=CE==3,
故本选项正确;
③由2xy+9=64可得2xy=55,
故本选项正确;
④∵x2+2xy+y2=64+55,
整理得,(x+y)2=119,
x+y=≠11,
故本选项错误;
∴正确结论有①②③.
故选:B.
6.解:由图可得,A与B的面积的和是E的面积;C与D的面积的和是F的面积;而E,F的面积的和是G的面积.
即A、B、C、D、E、F、G的面积之和为3个G的面积.
∵G的面积是62=36cm2,
∴A、B、C、D、E、F、G的面积之和为36×3=108cm2.
故选:D.
7.解:作AD⊥BC于D,如图所示:
则∠ADB=90°,
∵AB=AC,
∴BD=BC=6,
由勾股定理得:AD==8,
当BM⊥AC时,BM最小,
此时,∠BMC=90°,
∵△ABC的面积=AC BM=BC AD,
即×10×BM=×12×8,
解得:BM=9.6,
故选:B.
8.解:∵BC=5,AC==5,
∴S△ABC=×5×3=×AC×BD,
∴BD=3,
解法二:过A点做AE⊥BC交于点E,则易证三角形AEC全等三角形BDC,所以BD等于AE=3.
故选:A.
9.解:∵在△ABC中,∠C=90°,BC=8cm,CA=6cm,
∴AB=10cm,
∵点O为△ABC的三条角平分线的交点,
∴OE=OF=OD,
设OE=x,
∵S△ABC=S△OAB+S△OAC+S△OCB,
∴×6×8=OF×10+OE×6+OD×8,
∴5x+3x+4x=24,
∴x=2,
∴点O到AB的距离等于2.
故选:A.
二.填空题
10.解:∵直角三角形两直角边分别为6cm,8cm,
∴斜边长为 =10cm.
∵直角三角形面积=×一直角边长×另一直角边长=×斜边长×斜边的高,
代入题中条件,即可得:斜边高=4.8cm.
故答案为:4.8.
11.解:当AP=5时,Rt△ABC≌Rt△QPA,
理由是:∵∠C=90°,AQ⊥AC,
∴∠C=∠QAP=90°,
当AP=5=BC时,
在Rt△ABC和Rt△QPA中,,
∴Rt△ABC≌Rt△QPA(HL),
当AP=AC=10,AQ=BC=5时,△ABC≌△PQA,
故答案为:5或10.
12.解:①当△ABC为锐角三角形时,如图1所示,
∵AH⊥BC,
∴∠AHB=∠AHC=90°,
在Rt△ABH中,AB=41,AH=9,
根据勾股定理得:BH==40,
在Rt△AHC中,AC=15,AH=9,
根据勾股定理得:HC==12,
∴BC=BH+HC=40+12=52,
则S△ABC=BC AH=234;
②当△ABC为钝角三角形时,如图2所示,
由①得,BH=40,CH=12,
∴BC=BH﹣HC=40﹣12=28,
则S△ABC=BC AH=126.
综上,△ABC的面积为234或126.
故答案为:234或126.
13.解:由题意得,×π×()2=12.5π,
解得,AC=10,
×π×()2=4.5π,
解得,BC=6,
∴Rt△ABC的面积=×6×10=30cm2,
故答案为:30cm2.
14.
解:观察发现,
∵AB=BE,∠ACB=∠BDE=90°,
∴∠ABC+∠BAC=90°,∠ABC+∠EBD=90°,
∴∠BAC=∠EBD,
∴△ABC≌△BDE(AAS),
∴BC=ED,
∵AB2=AC2+BC2,
∴AB2=AC2+ED2=S1+S2,
即S1+S2=1,
同理S3+S4=3.
则S1+S2+S3+S4=1+3=4.
故答案为:4.
15.解:∵DE是AB的中垂线,
∴DA=DB,
设AD=x,则DB=x,CD=BC﹣BD=8﹣x,
在Rt△ACD中,∵AC2+CD2=AD2,
∴62+(8﹣x)2=x2,
解得x=,
∴CD=8﹣x=,
故答案为:.
三.解答题
16.解:由题意可得:在Rt△ABD和Rt△ACD中,
AB2﹣BD2=AD2,AC2﹣CD2=AD2,
设DC=x,
∵AB=17,BC=9,AC=10,
∴BD=9+x,
故172﹣(9+x)2=102﹣x2,
解得:x=6,
故AD===8,
则△ABC的面积为:×BC×AD=×9×8=36.
17.解:∵AC=AB=17,BC=16,AD是BC边上的中线,
∴BD=BC=8,AD⊥BC,
∴∠ADB=90°,
∴AD===15,
∴△ABC的面积==AC×BE,
∴BE==.
18.证明:连接DB,过点D作BC边上的高DF,则DF=EC=b﹣a.
∵S四边形ADCB=S△ACD+S△ABC=b2+ab.
又∵S四边形ADCB=S△ADB+S△DCB=c2+a(b﹣a)
∴b2+ab=c2+a(b﹣a)
∴a2+b2=c2
19.解:(1)∵∠BAD=90°,AD=3cm,AB=4cm,
∴BD==5,
∵BC=5,
∴△CBD是等腰三角形.
(2)作BE⊥CD于E,计算可得:
∵DE=3cm,BD=5
∴BE=4cm,
∴S△CBD=12cm2,
∵S△ABD=6cm2.
故四边形ABCD的面积为18cm2.
20.解:点A作AE⊥BC于点E,
∵AB=AC=20,BC=32,
∴BE=CE=BC.
∴AE===12.
设DE=x,则BD=16﹣x,CD=16+x,
在Rt△ADE中,AD2=AE2+DE2,即AD2=122+x2①,
在Rt△ADC中,AD2=CD2﹣AC2,即AD2=(16+x)2﹣202②,
①②联立得,122+x2=(16+x)2﹣202,解得x=9,
∴BD=16﹣9=7.
21.解:若△ABC是锐角三角形,则有a2+b2>c2(1分)
若△ABC是钝角三角形,∠C为钝角,则有a2+b2<c2.(2分)
当△ABC是锐角三角形时,
证明:过点A作AD⊥BC,垂足为D,设CD为x,则有BD=a﹣x(3分)
根据勾股定理,得b2﹣x2=AD2=c2﹣(a﹣x)2
即b2﹣x2=c2﹣a2+2ax﹣x2.
∴a2+b2=c2+2ax(5分)
∵a>0,x>0,
∴2ax>0.
∴a2+b2>c2.(6分)
当△ABC是钝角三角形时,
证明:过B作BD⊥AC,交AC的延长线于D.
设CD为y,则有BD2=a2﹣y2(7分)
根据勾股定理,得(b+y)2+a2﹣y2=c2.
即a2+b2+2by=c2.(9分)
∵b>0,y>0,
∴2by>0,
∴a2+b2<c2.(10分)
23.解:(1)如图1,
∵∠C=90°,AB=10cm,BC=6cm,
∴AC=8cm,
根据题意可得:PC=2cm,则AP=6cm,
故△ABP的面积为:×AP×BC=×6×6=18(cm2);
(2)如图2所示,过点P作PD⊥AB于点D,
∵BP平分∠CBA,
∴PD=PC.
在Rt△BPD与Rt△BPC中,,
∴Rt△BPD≌Rt△BPC(HL),
∴BD=BC=6 cm,
∴AD=10﹣6=4 cm.
设PC=x cm,则PA=(8﹣x)cm
在Rt△APD中,PD2+AD2=PA2,
即x2+42=(8﹣x)2,
解得:x=3,
∴当t=3秒时,BP平分∠CBA;
(3)如图3,
若P在边AC上时,BC=CP=6cm,
此时用的时间为6s,△BCP为等腰三角形;
若P在AB边上时,有3种情况:
①如图4,
若使BP=CB=6cm,此时AP=4cm,P运动的路程为12cm,
所以用的时间为12s,故t=12s时△BCP为等腰三角形;
②如图5,
若CP=BC=6cm,过C作斜边AB的高,根据面积法求得高为4.8cm,
根据勾股定理求得BP=7.2cm,
所以P运动的路程为18﹣7.2=10.8cm,
∴t的时间为10.8s,△BCP为等腰三角形;
③如图6,
若BP=CP时,则∠PCB=∠PBC,
∵∠ACP+∠BCP=90°,∠PBC+∠CAP=90°,∴∠ACP=∠CAP,∴PA=PC
∴PA=PB=5cm
∴P的路程为13cm,所以时间为13s时,△BCP为等腰三角形.
∴t=6s或13s或12s或 10.8s 时△BCP为等腰三角形.
一.选择题
1.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A.3cm2 B.4cm2 C.6cm2 D.12cm2
2.△ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是( )
A.4.8 B.4.8或3.8 C.3.8 D.5
3.直角三角形的两条直角边为a、b,斜边为c,斜边上的高为h,下列结论:①a2+b2=c2;②ab=ch;③.其中正确的是( )
A.① B.①②③ C.①② D.①③
4.如图所示,在△ABC中,AB=AC=5,BC=8,CD是AB边上的高,则线段AD的长度为( )
A. B. C. D.
5.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形的面积为64,小正方形的面积为9,若用x、y分别表示直角三角形的两直角边长(x>y),则下列四个说法:①x2+y2=64:②x﹣y=3;③2xy=55;④x+y=11.其中正确的是( )
A.①② B.①②③ C.①②④ D.①②③④
6.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若最大正方形G的边长是6cm,则正方形A,B,C,D,E,F,G的面积之和是( )
A.18cm2 B.36cm2 C.72cm2 D.108cm2
7.如图,在△ABC中,点M是AC边上一个动点.若AB=AC=10,BC=12,则BM的最小值为( )
A.8 B.9.6 C.10 D.4 5
8.如图所示,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为( )
A.3 B.2 C.4 D.
9.如图,在△ABC中,∠C=90°,O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且BC=8cm,CA=6cm,则点O到边AB的距离为( )
A.2cm B.3cm C.4cm D.5cm
二.填空题
10.直角三角形的两直角边的长分别为6cm、8cm,则斜边上高的长是 cm.
11.如图,有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于 AC的射线AX上运动,当AP= 时,才能使△ABC与△QPA全等.
12.△ABC中,AB=41,AC=15,高AH=9,则△ABC的面积是 .
13.如图,在Rt△ABC中,∠C=90°,以AC、BC为直径的半圆面积分别是12.5πcm2和4.5πcm2,则Rt△ABC的面积为 .
14.在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1,S2,S3,S4,则S1+S2+S3+S4= .
15.如图,在Rt△ABC中,∠C=90°,DE垂直平分AB,连接AD,若AC=6,BC=8,则CD的长为 .
三.解答题
16.如图,在△ABC中,AB=17,BC=9,AC=10,试求△ABC的面积.
17.如图,在等腰△ABC中,AC=AB=17,BC=16,AD是BC边上的中线,BE⊥AC,交AC于点E,求BE的长.
18.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明以灵感,他惊喜的发现,当两个全等的直角三角形如图摆放时,可以用“面积法”来证明.△ADE和△ACB是两直角边为a,b,斜边为c的全等的直角三角形,按如图所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
19.如图,四边形ABCD中,∠BAD=90°,AD=3cm,AB=4cm,BC=5cm,CD=6cm.
(1)连接BD,判断△CBD的形状;
(2)求四边形ABCD的面积S.
20.如图△ABC中,AB=AC=20,BC=32,D是BC上一点,且AD⊥AC,求BD的长.
21.△ABC中,BC=a,AC=b,AB=c.若∠C=90°,如图1,根据勾股定理,则a2+b2=c2.若△ABC不是直角三角形,如图2和图3,请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.
23.如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的面积;
(2)当t为几秒时,BP平分∠ABC;
(3)问t为何值时,△BCP为等腰三角形?
参考答案
一.选择题
1.解:将此长方形折叠,使点B与点D重合,∴BE=ED.
∵AD=9cm=AE+DE=AE+BE.
∴BE=9﹣AE,
根据勾股定理可知AB2+AE2=BE2.
解得AE=4.
∴△ABE的面积为3×4÷2=6.故选:C.
2.解:过A点作AF⊥BC于F,连接AP,
∵△ABC中,AB=AC=5,BC=8,
∴BF=4,
∴△ABF中,AF==3,
∴×8×3=×5×PD+×5×PE,
12=×5×(PD+PE)
PD+PE=4.8.
故选:A.
3.解:∵直角三角形的两条直角边为a、b,斜边为c,斜边上的高为h,
∴由勾股定理可知:a2+b2=c2,①正确;
这个直角三角形的面积=ab=ch,
∴ab=ch,②正确;
∴a2b2=c2h2,
∴====,③正确.
故选:B.
4.解:设AD=x
∵CD⊥AB,
∴∠D=90°,
∴CD2=BC2﹣BD2=AC2﹣AD2,
∴82﹣(5+x)2=52﹣x2,
∴x=,
∴AD=,
故选:D.
5.解:①∵△ABC为直角三角形,
∴根据勾股定理:x2+y2=AB2=64,
故本选项正确;
②由图可知,x﹣y=CE==3,
故本选项正确;
③由2xy+9=64可得2xy=55,
故本选项正确;
④∵x2+2xy+y2=64+55,
整理得,(x+y)2=119,
x+y=≠11,
故本选项错误;
∴正确结论有①②③.
故选:B.
6.解:由图可得,A与B的面积的和是E的面积;C与D的面积的和是F的面积;而E,F的面积的和是G的面积.
即A、B、C、D、E、F、G的面积之和为3个G的面积.
∵G的面积是62=36cm2,
∴A、B、C、D、E、F、G的面积之和为36×3=108cm2.
故选:D.
7.解:作AD⊥BC于D,如图所示:
则∠ADB=90°,
∵AB=AC,
∴BD=BC=6,
由勾股定理得:AD==8,
当BM⊥AC时,BM最小,
此时,∠BMC=90°,
∵△ABC的面积=AC BM=BC AD,
即×10×BM=×12×8,
解得:BM=9.6,
故选:B.
8.解:∵BC=5,AC==5,
∴S△ABC=×5×3=×AC×BD,
∴BD=3,
解法二:过A点做AE⊥BC交于点E,则易证三角形AEC全等三角形BDC,所以BD等于AE=3.
故选:A.
9.解:∵在△ABC中,∠C=90°,BC=8cm,CA=6cm,
∴AB=10cm,
∵点O为△ABC的三条角平分线的交点,
∴OE=OF=OD,
设OE=x,
∵S△ABC=S△OAB+S△OAC+S△OCB,
∴×6×8=OF×10+OE×6+OD×8,
∴5x+3x+4x=24,
∴x=2,
∴点O到AB的距离等于2.
故选:A.
二.填空题
10.解:∵直角三角形两直角边分别为6cm,8cm,
∴斜边长为 =10cm.
∵直角三角形面积=×一直角边长×另一直角边长=×斜边长×斜边的高,
代入题中条件,即可得:斜边高=4.8cm.
故答案为:4.8.
11.解:当AP=5时,Rt△ABC≌Rt△QPA,
理由是:∵∠C=90°,AQ⊥AC,
∴∠C=∠QAP=90°,
当AP=5=BC时,
在Rt△ABC和Rt△QPA中,,
∴Rt△ABC≌Rt△QPA(HL),
当AP=AC=10,AQ=BC=5时,△ABC≌△PQA,
故答案为:5或10.
12.解:①当△ABC为锐角三角形时,如图1所示,
∵AH⊥BC,
∴∠AHB=∠AHC=90°,
在Rt△ABH中,AB=41,AH=9,
根据勾股定理得:BH==40,
在Rt△AHC中,AC=15,AH=9,
根据勾股定理得:HC==12,
∴BC=BH+HC=40+12=52,
则S△ABC=BC AH=234;
②当△ABC为钝角三角形时,如图2所示,
由①得,BH=40,CH=12,
∴BC=BH﹣HC=40﹣12=28,
则S△ABC=BC AH=126.
综上,△ABC的面积为234或126.
故答案为:234或126.
13.解:由题意得,×π×()2=12.5π,
解得,AC=10,
×π×()2=4.5π,
解得,BC=6,
∴Rt△ABC的面积=×6×10=30cm2,
故答案为:30cm2.
14.
解:观察发现,
∵AB=BE,∠ACB=∠BDE=90°,
∴∠ABC+∠BAC=90°,∠ABC+∠EBD=90°,
∴∠BAC=∠EBD,
∴△ABC≌△BDE(AAS),
∴BC=ED,
∵AB2=AC2+BC2,
∴AB2=AC2+ED2=S1+S2,
即S1+S2=1,
同理S3+S4=3.
则S1+S2+S3+S4=1+3=4.
故答案为:4.
15.解:∵DE是AB的中垂线,
∴DA=DB,
设AD=x,则DB=x,CD=BC﹣BD=8﹣x,
在Rt△ACD中,∵AC2+CD2=AD2,
∴62+(8﹣x)2=x2,
解得x=,
∴CD=8﹣x=,
故答案为:.
三.解答题
16.解:由题意可得:在Rt△ABD和Rt△ACD中,
AB2﹣BD2=AD2,AC2﹣CD2=AD2,
设DC=x,
∵AB=17,BC=9,AC=10,
∴BD=9+x,
故172﹣(9+x)2=102﹣x2,
解得:x=6,
故AD===8,
则△ABC的面积为:×BC×AD=×9×8=36.
17.解:∵AC=AB=17,BC=16,AD是BC边上的中线,
∴BD=BC=8,AD⊥BC,
∴∠ADB=90°,
∴AD===15,
∴△ABC的面积==AC×BE,
∴BE==.
18.证明:连接DB,过点D作BC边上的高DF,则DF=EC=b﹣a.
∵S四边形ADCB=S△ACD+S△ABC=b2+ab.
又∵S四边形ADCB=S△ADB+S△DCB=c2+a(b﹣a)
∴b2+ab=c2+a(b﹣a)
∴a2+b2=c2
19.解:(1)∵∠BAD=90°,AD=3cm,AB=4cm,
∴BD==5,
∵BC=5,
∴△CBD是等腰三角形.
(2)作BE⊥CD于E,计算可得:
∵DE=3cm,BD=5
∴BE=4cm,
∴S△CBD=12cm2,
∵S△ABD=6cm2.
故四边形ABCD的面积为18cm2.
20.解:点A作AE⊥BC于点E,
∵AB=AC=20,BC=32,
∴BE=CE=BC.
∴AE===12.
设DE=x,则BD=16﹣x,CD=16+x,
在Rt△ADE中,AD2=AE2+DE2,即AD2=122+x2①,
在Rt△ADC中,AD2=CD2﹣AC2,即AD2=(16+x)2﹣202②,
①②联立得,122+x2=(16+x)2﹣202,解得x=9,
∴BD=16﹣9=7.
21.解:若△ABC是锐角三角形,则有a2+b2>c2(1分)
若△ABC是钝角三角形,∠C为钝角,则有a2+b2<c2.(2分)
当△ABC是锐角三角形时,
证明:过点A作AD⊥BC,垂足为D,设CD为x,则有BD=a﹣x(3分)
根据勾股定理,得b2﹣x2=AD2=c2﹣(a﹣x)2
即b2﹣x2=c2﹣a2+2ax﹣x2.
∴a2+b2=c2+2ax(5分)
∵a>0,x>0,
∴2ax>0.
∴a2+b2>c2.(6分)
当△ABC是钝角三角形时,
证明:过B作BD⊥AC,交AC的延长线于D.
设CD为y,则有BD2=a2﹣y2(7分)
根据勾股定理,得(b+y)2+a2﹣y2=c2.
即a2+b2+2by=c2.(9分)
∵b>0,y>0,
∴2by>0,
∴a2+b2<c2.(10分)
23.解:(1)如图1,
∵∠C=90°,AB=10cm,BC=6cm,
∴AC=8cm,
根据题意可得:PC=2cm,则AP=6cm,
故△ABP的面积为:×AP×BC=×6×6=18(cm2);
(2)如图2所示,过点P作PD⊥AB于点D,
∵BP平分∠CBA,
∴PD=PC.
在Rt△BPD与Rt△BPC中,,
∴Rt△BPD≌Rt△BPC(HL),
∴BD=BC=6 cm,
∴AD=10﹣6=4 cm.
设PC=x cm,则PA=(8﹣x)cm
在Rt△APD中,PD2+AD2=PA2,
即x2+42=(8﹣x)2,
解得:x=3,
∴当t=3秒时,BP平分∠CBA;
(3)如图3,
若P在边AC上时,BC=CP=6cm,
此时用的时间为6s,△BCP为等腰三角形;
若P在AB边上时,有3种情况:
①如图4,
若使BP=CB=6cm,此时AP=4cm,P运动的路程为12cm,
所以用的时间为12s,故t=12s时△BCP为等腰三角形;
②如图5,
若CP=BC=6cm,过C作斜边AB的高,根据面积法求得高为4.8cm,
根据勾股定理求得BP=7.2cm,
所以P运动的路程为18﹣7.2=10.8cm,
∴t的时间为10.8s,△BCP为等腰三角形;
③如图6,
若BP=CP时,则∠PCB=∠PBC,
∵∠ACP+∠BCP=90°,∠PBC+∠CAP=90°,∴∠ACP=∠CAP,∴PA=PC
∴PA=PB=5cm
∴P的路程为13cm,所以时间为13s时,△BCP为等腰三角形.
∴t=6s或13s或12s或 10.8s 时△BCP为等腰三角形.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
