2.8 直角三角形全等的判定 课件(共18张PPT)
文档属性
| 名称 | 2.8 直角三角形全等的判定 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 244.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 17:38:36 | ||
图片预览


文档简介
(共18张PPT)
2.8 直角三角形全等的判定
浙教版八上数学
领悟的,SSA------HL
1.在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等(简记为SAS)
温故知新:
2.在两个三角形中,如果有两个角及它们的夹边对应相等,
那么这两个三角形全等(简记为ASA)
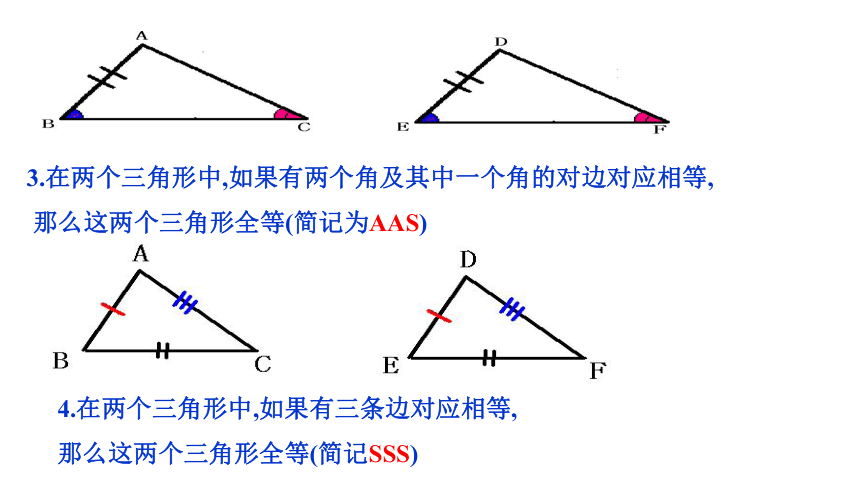
3.在两个三角形中,如果有两个角及其中一个角的对边对应相等,
那么这两个三角形全等(简记为AAS)
4.在两个三角形中,如果有三条边对应相等,
那么这两个三角形全等(简记SSS)
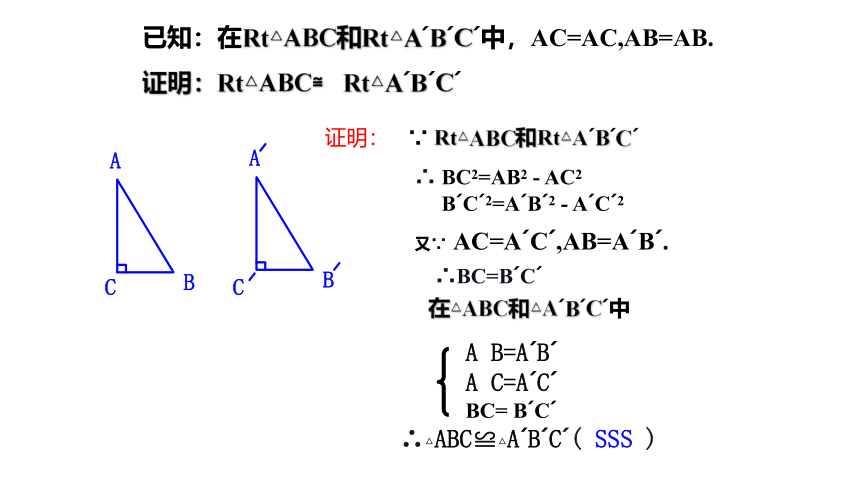
已知:在Rt△ABC和Rt△A B C 中,AC=AC,AB=AB.
证明:Rt△ABC≌ Rt△A B C
∵ Rt△ABC和Rt△A B C
∴ BC2=AB2 - AC2
B C 2=A B 2 - A C 2
又∵ AC=A C ,AB=A B .
∴BC=B C
在△ABC和△A B C 中
A B=A B
A C=A C BC= B C
∴△ABC≌△A B C ( SSS )
证明:
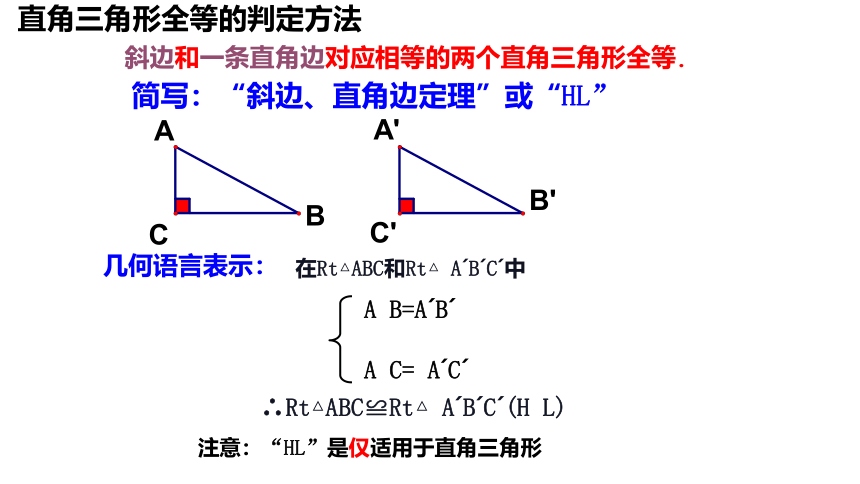
简写:“斜边、直角边定理”或“HL”
A B=A B
A C= A C
∴Rt△ABC≌Rt△ A B C (H L)
直角三角形全等的判定方法
几何语言表示:
斜边和一条直角边对应相等的两个直角三角形全等.
在Rt△ABC和Rt△ A B C 中
注意:“HL”是仅适用于直角三角形
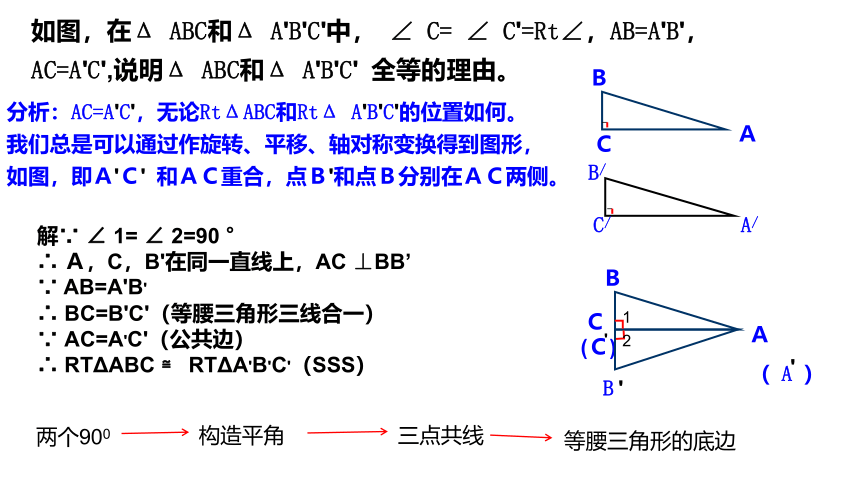
分析:AC=A'C',无论RtΔABC和RtΔ A'B'C'的位置如何。
我们总是可以通过作旋转、平移、轴对称变换得到图形,如图,即A'C' 和AC重合,点B'和点B分别在AC两侧。
A
C
B
A/
C/
B/
如图,在Δ ABC和Δ A'B'C'中, ∠ C= ∠ C'=Rt∠,AB=A'B', AC=A'C',说明Δ ABC和Δ A'B'C' 全等的理由。
( A )
'
'
(C)
A
C
B
B
'
┓
┓
1
2
解∵ ∠ 1= ∠ 2=90 °
∴ A,C,B'在同一直线上,AC ⊥BB’
∵ AB=A'B'
∴ BC=B'C'(等腰三角形三线合一)
∵ AC=A'C'(公共边)
∴ RTΔABC ≌ RTΔA'B'C'(SSS)
构造平角
两个900
三点共线
等腰三角形的底边
直角三角形全等的判定
一般三角形全等的判定
SAS
ASA
AAS
SSS
SAS
ASA
AAS
HL
SSS
知识小结:
(1) _______,∠A=∠D ( ASA )
(2) AC=DF,________ (SAS)
(3) AB=DE,BC=EF ( )
(4) AC=DF, ______ (HL)
(5) ∠A=∠D, BC=EF ( )
B
C
A
E
F
D
1.把下列说明Rt△ABC≌Rt△DEF的条件或根据补充完整.
AC=DF
BC=EF
HL
AB=DE
AAS
学以致用:
角平分线的性质定理:
角的平分线上的点到角的两边的距离相等.
几何语言:∵OC是∠AOB的平分线,
PD⊥OA,PE⊥OB,∴PD=PE.
O
A
B
C
P
D
E
┐
┐
说出角平分线的性质定理的逆命题。
角的内部,到角两边距离相等的点,在这个角的平分线上。
2、如图,已知 P是∠AOB内部一点,PD⊥OA, PE⊥OB,D,E分别是垂足,且PD=PE,则点P在∠AOB的平分线上.请说明理由。
O
P
D
E
A
B
1
2
解: 作射线OP
在Rt Δ PDO 和 RtΔ PEO中:
PD=PE
OP=OP
∴ RtΔ PDO ≌ RtΔ PEO(HL)
∵ PD ┴ OA,PE ┴ OB,
∴ ∠ PDO= ∠ PEO=Rt ∠
∴ ∠ 1= ∠ 2,即点P在∠ AOB的平分线上。
同学们,你得出什么结论?
角平分线的判定:
角的内部,到角两边距离相等的点,在这个角的平分线上。
新知讲解
判定定理:角的内部到角的两边的距离相等的点在角的平分线上.
P
A
O
B
C
D
E
定理的作用:判断点是否在角平分线上.
几何语言:
∵ PD⊥OA,PE⊥OB,PD=PE.
∴点P 在∠AOB的平分线上.
角的平分线的性质定理与判定定理的关系
点在角的平分线上
性质定理
(角的内部)点到角的两边的距离相等
判定定理
新知讲解
3. 已知:如图,△ABC的角平分线BM,CN相交于点P,
求证:(1)点P到三边AB,BC,CA的距离相等.(2)点P在∠A的平分线上
证明:(1)过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE.同理PE=PF.∴PD=PE=PF.
点P到三边AB,BC,CA的距离相等.
A
B
C
P
N
M
D
E
F
(2)
∵PD⊥AB,PF⊥AC,且PD=PF
∴点P在∠A的平分线上.
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.
三角形三条角平分线的交点,叫做三角形的内心。
1 . 如图,在△ABC和△ABD中,AC⊥BC, AD⊥BD,垂足分C,D,BD=AC.
求证:BC=AD.
A
B
D
C
┓
┓
=
证明:
∵ AC⊥BC,AD⊥BD(已知),
∴∠C=∠D=90°.
在Rt△ABC 和 Rt△BAD中,
∴Rt△ABC≌Rt△BAD(HL),
∴BC=AD(全等三角形的对应边相等).
.
当堂检测:
2、如图,AC=AD,∠C=∠D=Rt∠ ,你能说明BC与BD相等吗?
解:BC=BD,理由如下:
AB=AB,
AC=AD.
∴ Rt△ACB≌Rt△ADB (HL).
∴BC=BD(全等三角形对应边相等).
在Rt△ACB和Rt△ADB中
3、已知:如图,在△ABC中,D是BC的中点,
DE⊥AB于点E,DF⊥AC于点F,且DE=DF.
求证:AB=AC.
D
B
C
A
E
F
┓
┓
证明:∵ DE⊥AB,DF⊥AC∴ ∠BED=∠CFD=Rt∠
∵ D是BC的中点 ∴ BD=CD
在RtΔBDE 和 RtΔCDF中,
∴ RtΔBDE ≌ RtΔCDF(HL)
∴ ∠B=∠C(全等三角形的对应角相等)
∴ AB=AC(在同一个三角形中,等角对等边)
BD=CD,
DE=DF
.
4:如图,∠B=∠E=Rt∠,AB=AE,∠1=∠2,则∠3=∠4 ,请说明理由。
∵ ∠1=∠2
∴AC=AD
∴在Rt△ABC和Rt△ADE中
∵ ∠B=∠E=Rt∠
AC=AD
AB=AE
∴ Rt△ABC ≌ Rt△ADE ( )
HL
∴ ∠3=∠4
2.再过点M作OA的垂线
1.如图:在已知∠AOB的两边OA,OB上分别取点M,N,使OM=ON
3.过点N作OB的垂线,两垂线交于点P
4.那么射线OP就是∠AOB的平分线.
A
B
O
●
●
●P
M
N
5.给你一块有刻度的三角板,作出∠AOB的平分线
连续递推,豁然开朗
6.已知:如图,在△ABC中,AD⊥BC于点D,E是AC上一点,且BF=AC,DF=DC.求证:BE⊥AC.
证明:
∵AD⊥BC
∴∠BDF=∠ADC=900
在Rt△BDF和Rt△ADC中
∴ Rt△BDF≌ Rt△ADC ( )
HL
BF=AC,
DF=DC
A
B
C
D
E
F
┓
⌒
⌒
⌒
⌒
1
2
3
4
∴∠1=∠2
∵∠3=∠4
∵∠1+∠3=900
∴∠2+∠4=900
∴BE⊥AC
2.8 直角三角形全等的判定
浙教版八上数学
领悟的,SSA------HL
1.在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等(简记为SAS)
温故知新:
2.在两个三角形中,如果有两个角及它们的夹边对应相等,
那么这两个三角形全等(简记为ASA)
3.在两个三角形中,如果有两个角及其中一个角的对边对应相等,
那么这两个三角形全等(简记为AAS)
4.在两个三角形中,如果有三条边对应相等,
那么这两个三角形全等(简记SSS)
已知:在Rt△ABC和Rt△A B C 中,AC=AC,AB=AB.
证明:Rt△ABC≌ Rt△A B C
∵ Rt△ABC和Rt△A B C
∴ BC2=AB2 - AC2
B C 2=A B 2 - A C 2
又∵ AC=A C ,AB=A B .
∴BC=B C
在△ABC和△A B C 中
A B=A B
A C=A C BC= B C
∴△ABC≌△A B C ( SSS )
证明:
简写:“斜边、直角边定理”或“HL”
A B=A B
A C= A C
∴Rt△ABC≌Rt△ A B C (H L)
直角三角形全等的判定方法
几何语言表示:
斜边和一条直角边对应相等的两个直角三角形全等.
在Rt△ABC和Rt△ A B C 中
注意:“HL”是仅适用于直角三角形
分析:AC=A'C',无论RtΔABC和RtΔ A'B'C'的位置如何。
我们总是可以通过作旋转、平移、轴对称变换得到图形,如图,即A'C' 和AC重合,点B'和点B分别在AC两侧。
A
C
B
A/
C/
B/
如图,在Δ ABC和Δ A'B'C'中, ∠ C= ∠ C'=Rt∠,AB=A'B', AC=A'C',说明Δ ABC和Δ A'B'C' 全等的理由。
( A )
'
'
(C)
A
C
B
B
'
┓
┓
1
2
解∵ ∠ 1= ∠ 2=90 °
∴ A,C,B'在同一直线上,AC ⊥BB’
∵ AB=A'B'
∴ BC=B'C'(等腰三角形三线合一)
∵ AC=A'C'(公共边)
∴ RTΔABC ≌ RTΔA'B'C'(SSS)
构造平角
两个900
三点共线
等腰三角形的底边
直角三角形全等的判定
一般三角形全等的判定
SAS
ASA
AAS
SSS
SAS
ASA
AAS
HL
SSS
知识小结:
(1) _______,∠A=∠D ( ASA )
(2) AC=DF,________ (SAS)
(3) AB=DE,BC=EF ( )
(4) AC=DF, ______ (HL)
(5) ∠A=∠D, BC=EF ( )
B
C
A
E
F
D
1.把下列说明Rt△ABC≌Rt△DEF的条件或根据补充完整.
AC=DF
BC=EF
HL
AB=DE
AAS
学以致用:
角平分线的性质定理:
角的平分线上的点到角的两边的距离相等.
几何语言:∵OC是∠AOB的平分线,
PD⊥OA,PE⊥OB,∴PD=PE.
O
A
B
C
P
D
E
┐
┐
说出角平分线的性质定理的逆命题。
角的内部,到角两边距离相等的点,在这个角的平分线上。
2、如图,已知 P是∠AOB内部一点,PD⊥OA, PE⊥OB,D,E分别是垂足,且PD=PE,则点P在∠AOB的平分线上.请说明理由。
O
P
D
E
A
B
1
2
解: 作射线OP
在Rt Δ PDO 和 RtΔ PEO中:
PD=PE
OP=OP
∴ RtΔ PDO ≌ RtΔ PEO(HL)
∵ PD ┴ OA,PE ┴ OB,
∴ ∠ PDO= ∠ PEO=Rt ∠
∴ ∠ 1= ∠ 2,即点P在∠ AOB的平分线上。
同学们,你得出什么结论?
角平分线的判定:
角的内部,到角两边距离相等的点,在这个角的平分线上。
新知讲解
判定定理:角的内部到角的两边的距离相等的点在角的平分线上.
P
A
O
B
C
D
E
定理的作用:判断点是否在角平分线上.
几何语言:
∵ PD⊥OA,PE⊥OB,PD=PE.
∴点P 在∠AOB的平分线上.
角的平分线的性质定理与判定定理的关系
点在角的平分线上
性质定理
(角的内部)点到角的两边的距离相等
判定定理
新知讲解
3. 已知:如图,△ABC的角平分线BM,CN相交于点P,
求证:(1)点P到三边AB,BC,CA的距离相等.(2)点P在∠A的平分线上
证明:(1)过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE.同理PE=PF.∴PD=PE=PF.
点P到三边AB,BC,CA的距离相等.
A
B
C
P
N
M
D
E
F
(2)
∵PD⊥AB,PF⊥AC,且PD=PF
∴点P在∠A的平分线上.
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.
三角形三条角平分线的交点,叫做三角形的内心。
1 . 如图,在△ABC和△ABD中,AC⊥BC, AD⊥BD,垂足分C,D,BD=AC.
求证:BC=AD.
A
B
D
C
┓
┓
=
证明:
∵ AC⊥BC,AD⊥BD(已知),
∴∠C=∠D=90°.
在Rt△ABC 和 Rt△BAD中,
∴Rt△ABC≌Rt△BAD(HL),
∴BC=AD(全等三角形的对应边相等).
.
当堂检测:
2、如图,AC=AD,∠C=∠D=Rt∠ ,你能说明BC与BD相等吗?
解:BC=BD,理由如下:
AB=AB,
AC=AD.
∴ Rt△ACB≌Rt△ADB (HL).
∴BC=BD(全等三角形对应边相等).
在Rt△ACB和Rt△ADB中
3、已知:如图,在△ABC中,D是BC的中点,
DE⊥AB于点E,DF⊥AC于点F,且DE=DF.
求证:AB=AC.
D
B
C
A
E
F
┓
┓
证明:∵ DE⊥AB,DF⊥AC∴ ∠BED=∠CFD=Rt∠
∵ D是BC的中点 ∴ BD=CD
在RtΔBDE 和 RtΔCDF中,
∴ RtΔBDE ≌ RtΔCDF(HL)
∴ ∠B=∠C(全等三角形的对应角相等)
∴ AB=AC(在同一个三角形中,等角对等边)
BD=CD,
DE=DF
.
4:如图,∠B=∠E=Rt∠,AB=AE,∠1=∠2,则∠3=∠4 ,请说明理由。
∵ ∠1=∠2
∴AC=AD
∴在Rt△ABC和Rt△ADE中
∵ ∠B=∠E=Rt∠
AC=AD
AB=AE
∴ Rt△ABC ≌ Rt△ADE ( )
HL
∴ ∠3=∠4
2.再过点M作OA的垂线
1.如图:在已知∠AOB的两边OA,OB上分别取点M,N,使OM=ON
3.过点N作OB的垂线,两垂线交于点P
4.那么射线OP就是∠AOB的平分线.
A
B
O
●
●
●P
M
N
5.给你一块有刻度的三角板,作出∠AOB的平分线
连续递推,豁然开朗
6.已知:如图,在△ABC中,AD⊥BC于点D,E是AC上一点,且BF=AC,DF=DC.求证:BE⊥AC.
证明:
∵AD⊥BC
∴∠BDF=∠ADC=900
在Rt△BDF和Rt△ADC中
∴ Rt△BDF≌ Rt△ADC ( )
HL
BF=AC,
DF=DC
A
B
C
D
E
F
┓
⌒
⌒
⌒
⌒
1
2
3
4
∴∠1=∠2
∵∠3=∠4
∵∠1+∠3=900
∴∠2+∠4=900
∴BE⊥AC
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
