2022-2023学年浙教版七年级数学上册3.1平方根 课件(共17张PPT)
文档属性
| 名称 | 2022-2023学年浙教版七年级数学上册3.1平方根 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 325.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 08:13:16 | ||
图片预览




文档简介
(共17张PPT)
第3章 实数
3.1 平方根
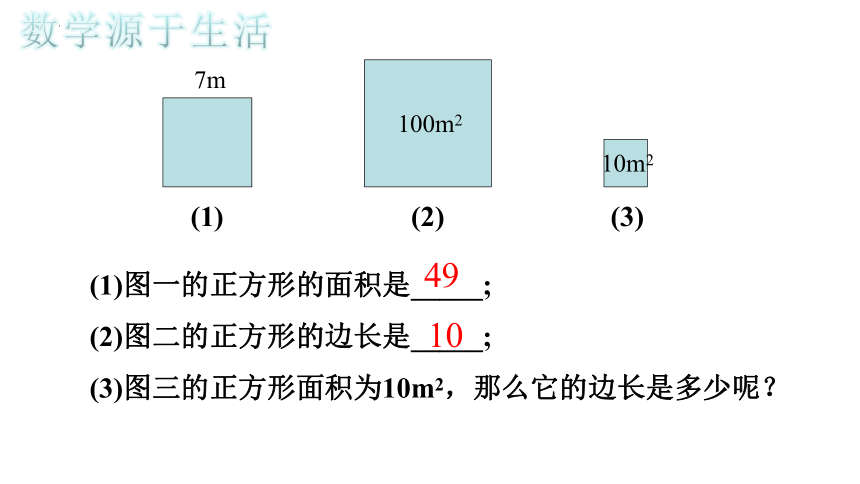
(1)图一的正方形的面积是_____;
(2)图二的正方形的边长是_____;
(3)图三的正方形面积为10m2,那么它的边长是多少呢?
数学源于生活
(1)
(2)
(3)
7m
100m2
10m2
49
10
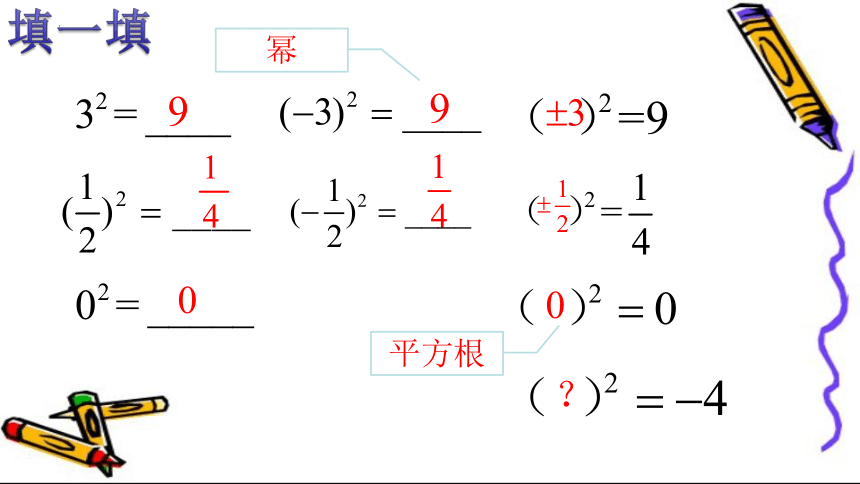
填一填
9
9
0
0
?
平方根
幂
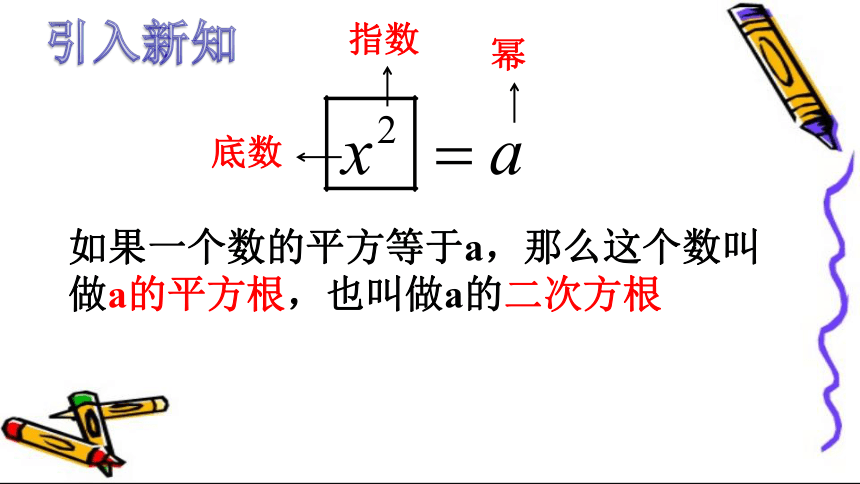
如果一个数的平方等于a,那么这个数叫做a的平方根,也叫做a的二次方根
指数
底数
幂
引入新知
合作探究
说一说他们的平方根? 4,9,0,0.01,
议一议:
(1)1个正数有几个平方根?
(2)0有几个平方根?
(3)负数呢?
2
1、正数有__个平方根,它们互为_____;
2、0有____个平方根,它是_______;
3、负数______平方根。
合作探究
没有
0
1
相反数
平方根的性质:
那如何表示平方根呢??
读作:根号
引入新知
读作:根号
(正数a)
正平方根,读作:根号a,
(正数a)
负平方根,读作:负根号a
(正数a)
平方根,读作:正负根号a
被开方数
求一个数的平方根的运算,叫做开平方
引入新知
开平方
平方
互为逆运算
已知指数和幂,求底数
已知底数和指数,求幂
是不是所有的数都能进行开平方运算?
1、求下列各数的平方根
(1)9 (2) (3)0 (4) (5)(-3)2 (6)
例题讲解
算数平方根:正数的正平方根和0的平方根
练一练 下列各数有没有平方根?若有,求它的算数平方根
121 (-3)2 -0.36 6
2、先说出下列各式的意义,再计算
(1) (2) (3) (4)
解: (1) 表示 的平方根
(2) 表示 225 的算数平方根
(3) 表示 的负平方根
(4) 表示 81 平方根
巩固练习
1、下列各数有没有平方根?如果有,求出它的平方根,如果没有,请说明理由
100,0.0001,0,
2、已知一个长方形的长是宽的2倍,面积为72cm2,求这个长方形的周长。
反思与提高
1、你有什么收获呢?
2、你还有什么疑问么?
课堂小结:
1、如果一个数的平方等于a,那么这个数叫做a的平方根,也叫做a的二次方根。
2、一个正数有正负两个平方根,它们互为相反数
3、 0的平方根是0
4、负数没有平方根
5、正数的正平方根和0的平方根称为算数平方根
课堂小结:
6、一个正数a的平方根表示为
7、一个非负数a的算数平方根表示为
8、求一个数的平方根的运算,叫做开平方.
探究活动
观察右图,每个小正方形的边长均为1,我们可以得到小正方形的面积为1. .
(1)图中阴影正方形的面积是多少 它的边长是多少
(2)估计 2 的值在哪两个整数之间 .
第3章 实数
3.1 平方根
(1)图一的正方形的面积是_____;
(2)图二的正方形的边长是_____;
(3)图三的正方形面积为10m2,那么它的边长是多少呢?
数学源于生活
(1)
(2)
(3)
7m
100m2
10m2
49
10
填一填
9
9
0
0
?
平方根
幂
如果一个数的平方等于a,那么这个数叫做a的平方根,也叫做a的二次方根
指数
底数
幂
引入新知
合作探究
说一说他们的平方根? 4,9,0,0.01,
议一议:
(1)1个正数有几个平方根?
(2)0有几个平方根?
(3)负数呢?
2
1、正数有__个平方根,它们互为_____;
2、0有____个平方根,它是_______;
3、负数______平方根。
合作探究
没有
0
1
相反数
平方根的性质:
那如何表示平方根呢??
读作:根号
引入新知
读作:根号
(正数a)
正平方根,读作:根号a,
(正数a)
负平方根,读作:负根号a
(正数a)
平方根,读作:正负根号a
被开方数
求一个数的平方根的运算,叫做开平方
引入新知
开平方
平方
互为逆运算
已知指数和幂,求底数
已知底数和指数,求幂
是不是所有的数都能进行开平方运算?
1、求下列各数的平方根
(1)9 (2) (3)0 (4) (5)(-3)2 (6)
例题讲解
算数平方根:正数的正平方根和0的平方根
练一练 下列各数有没有平方根?若有,求它的算数平方根
121 (-3)2 -0.36 6
2、先说出下列各式的意义,再计算
(1) (2) (3) (4)
解: (1) 表示 的平方根
(2) 表示 225 的算数平方根
(3) 表示 的负平方根
(4) 表示 81 平方根
巩固练习
1、下列各数有没有平方根?如果有,求出它的平方根,如果没有,请说明理由
100,0.0001,0,
2、已知一个长方形的长是宽的2倍,面积为72cm2,求这个长方形的周长。
反思与提高
1、你有什么收获呢?
2、你还有什么疑问么?
课堂小结:
1、如果一个数的平方等于a,那么这个数叫做a的平方根,也叫做a的二次方根。
2、一个正数有正负两个平方根,它们互为相反数
3、 0的平方根是0
4、负数没有平方根
5、正数的正平方根和0的平方根称为算数平方根
课堂小结:
6、一个正数a的平方根表示为
7、一个非负数a的算数平方根表示为
8、求一个数的平方根的运算,叫做开平方.
探究活动
观察右图,每个小正方形的边长均为1,我们可以得到小正方形的面积为1. .
(1)图中阴影正方形的面积是多少 它的边长是多少
(2)估计 2 的值在哪两个整数之间 .
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
