2.8 直角三角形全等的判定

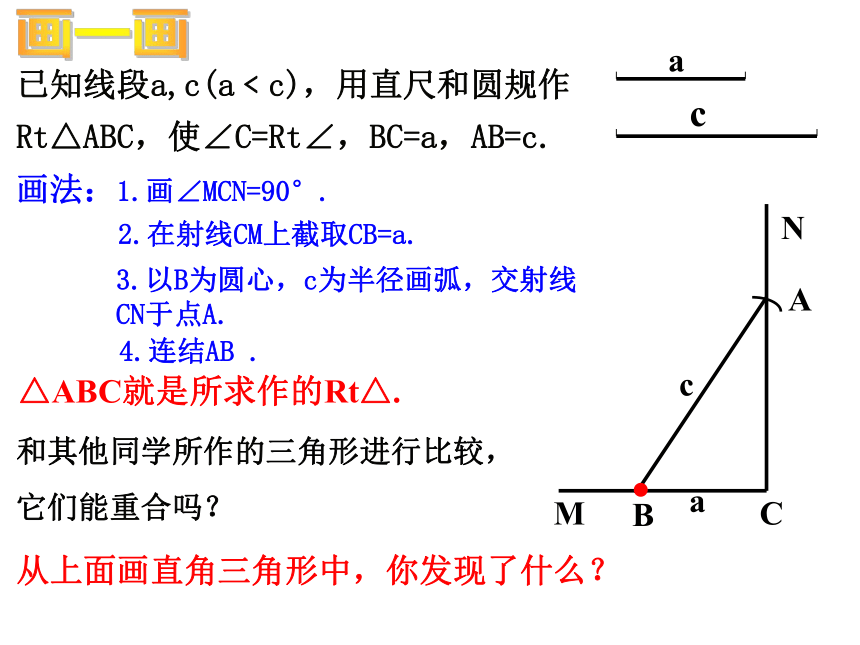
课件12张PPT。2.8 直角三角形全等的判定1、判定两个三角形全等有什么方法？知识回顾SSS，SAS，ASA，AAS.2、在用SAS判定两个三角形全等时，要注意什么？这个角是已知两边的夹角。已知线段a,c(a﹤c)，用直尺和圆规作Rt△ABC，使∠C=Rt∠，BC=a，AB=c.画法：1.画∠MCN=90°.3.以B为圆心，c为半径画弧，交射线CN于点A.4.连结AB .△ABC就是所求作的Rt△.MCNaBcA2.在射线CM上截取CB=a.画一画从上面画直角三角形中，你发现了什么？和其他同学所作的三角形进行比较，
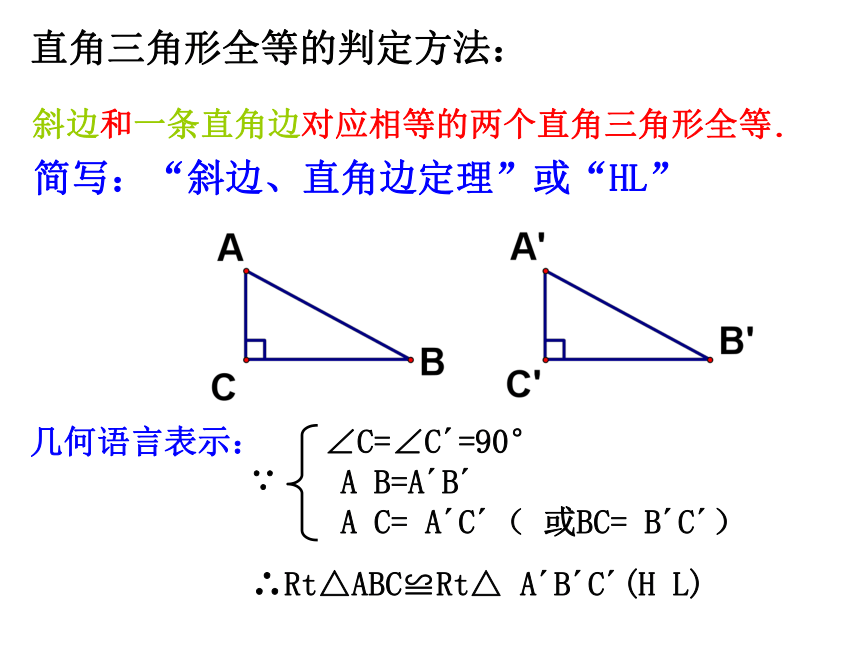
它们能重合吗？简写：“斜边、直角边定理”或“HL”∠C=∠C′=90°
A B=A′B′
A C= A′C′（ 或BC= B′C′）∴Rt△ABC≌Rt△ A′B′C′(H L)直角三角形全等的判定方法：∵几何语言表示：斜边和一条直角边对应相等的两个直角三角形全等.已知：如图，在△ABC和△A’B’C’中，
∠C=∠C’=Rt∠，AB=A’B’，AC=A’C’.
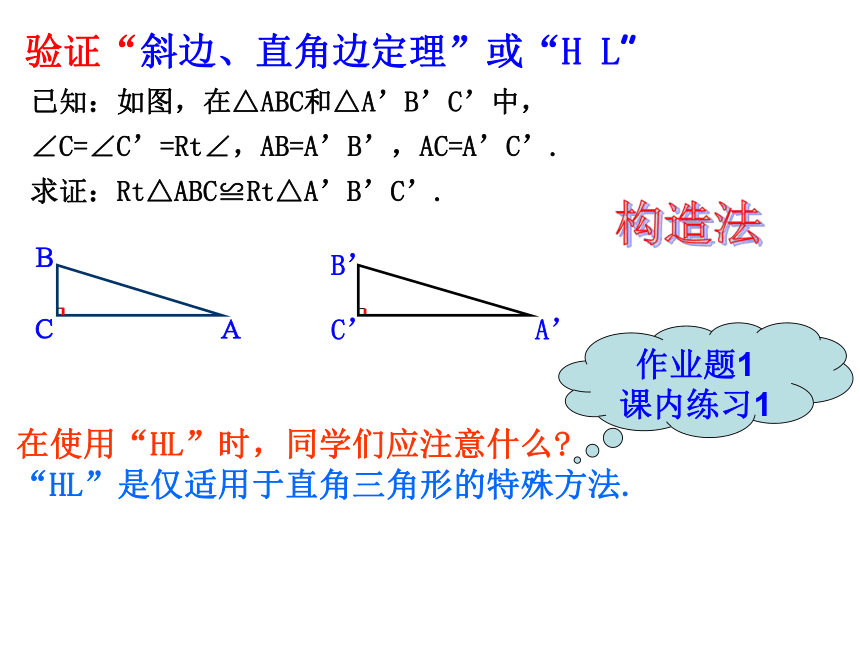
求证：Rt△ABC≌Rt△A’B’C’.验证“斜边、直角边定理”或“H L”在使用“HL”时，同学们应注意什么?
“HL”是仅适用于直角三角形的特殊方法.作业题1
课内练习1构造法1、已知：如图，在△ABC中，D是BC的中点,
DE⊥AB于点E，DF⊥AC于点F，且DE=DF.
求证：AB=AC.证明：∵ DE⊥AB，DF⊥AC
∴ ∠BED=∠CFD=RT∠
∵ D是BC的中点
∴ BD=CD
∵ DE=DF
∴ RtΔBDE ≌ RtΔCDF（HL）
∴ ∠B=∠C（全等三角形的对应角相等）
∴ AB=AC（在同一个三角形中，等角对等边）例 已知：如图，P是∠AOB内一点，PD⊥OA， PE⊥OB，D，E分别是垂足，且PD=PE.
求证：点P在∠AOB的平分线上.角的内部，到角两边距离相等的点，在这个角的平分线上。角平分线性质定理的逆定理：作业题4
课内练习24、已知：如图，∠ABD=∠ACD=90°，∠1=∠2.
求证：AD平分∠BAC.2、已知△ABC，用直尺和圆规作一点P，使它到三边
的距离都相等（只要求作出图形，并保留作图痕迹）.P1、已知：如图，∠B=∠E=Rt∠，AB=AE，∠1=∠2.
求证：∠3=∠4.练习：2、已知：如图，AB⊥BD于点B，CD⊥BD于点D，P是BD上一点，且AP=PC，AP⊥PC. 求证：△ABP≌△PDC.证明：∵ AB⊥BD，CD⊥BD∴ ∠ B= ∠ D=Rt∠∵ AP⊥PC∴ ∠ APB+ ∠ CPD=900∴ ∠ APB+ ∠ A=900∴ ∠ CPD= ∠ A（同角的余角相等）∵ AP=PC∴ △ABP≌△PDC（AAS）1、如图，两根长度为12米的绳子，一端系在旗杆上，另一端分别固定在地面两个木桩上，两个木桩离旗杆底部的距离相等吗？请说明你的理由。应用练习：小 结直角三角形全等的判定定理：
SSS，SAS，ASA，AAS，HL（特有）.
切记!!! 两边及其中一边的对角对应相等的两个三角形不一定全等.
角平分线的性质定理：
①角平分线上的点到角两边的距离相等；
②角的内部，到角两边距离相等的点，在这个角的平分线上。