浙教版八年级下册5.1矩形课件(共16张PPT)
文档属性
| 名称 | 浙教版八年级下册5.1矩形课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 19:45:43 | ||
图片预览






文档简介
(共16张PPT)
5.1矩形(1)
新知导入
议一议
用6根火柴棒首尾相接摆成一个平行四边形(如图)
思考(1)能摆成多少个不同的平行四边形?它们有什么共同特点?
(2)在这些平行四边形中,有没有面积最大的一个平行四边形?
说出你的理由.
说一说
有一个角是直角的平行四边形叫做矩形。
有一个直角
平行四边形
矩形
矩形是一种特殊的平行四边形。
小学里学过的长方形、正方形都是矩形
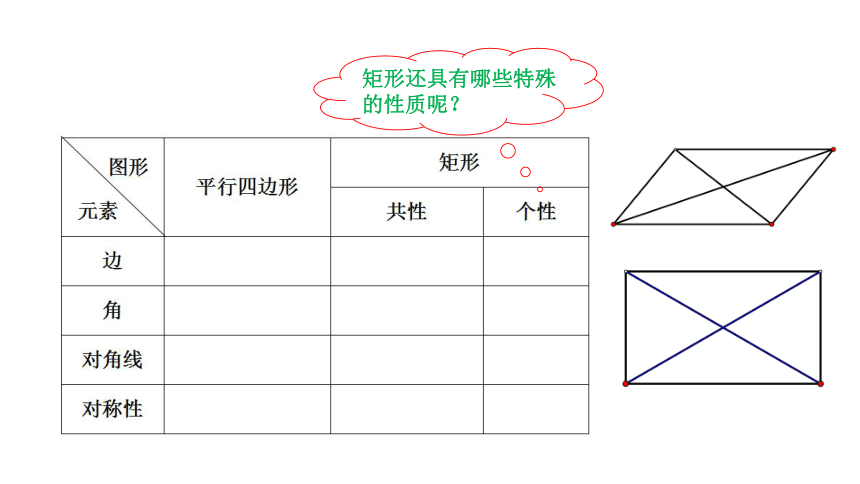
矩形还具有哪些特殊的性质呢?
合作探究
矩形还具有哪些特殊的性质呢?
两组对边分别平行且相等
两组对边分别平行且相等
两组对角分别相等
两组对角分别相等
互相平分
互相平分
中心对称图形
中心对称图形
无
四个角都是直角
相等
对称图形轴
新知讲解
提炼概念
矩形性质定理1: 矩形的四个角都是直角.
几何语言:
∵四边形ABCD是矩形,∴∠A=∠B=∠C=∠D=90°
矩形的对角线相等.
这个命题正确吗?试着说说你的理由.
已知:四边形ABCD是矩形.
求证:AC = BD.
证明:在矩形ABCD中,∵∠ABC = ∠DCB = 90°,
又∵AB = DC , BC = CB,
∴△ABC≌△DCB,∴AC = BD.
矩形的性质定理2:矩形的对角线相等.
符号语言:∵四边形ABCD是矩形,∴AC = BD.
归纳概念
典例精讲
新知讲解
例1:已知:如图,在矩形ABCD中对角线AC、BD相交于点O,
∠AOD=120°,AB=4 cm.
(1)判断△AOB的形状;
(2)求矩形对角线的长.
解:(1)∵四边形ABCD是矩形,∴AC=BD,
∴OA=OC=OB=OD,∴OA=OC=OB=OD,∴∠AOB=60°,∴△AOB是等边三角形;
(2)∵AB=4,
∴AC=BD=2AB=8 cm,
即矩形对角线的长为8 cm.
想一想:
矩形是轴对称图形吗?如果是,它有几条对称轴 是中心对称图形吗?
矩形是轴对称图形,它至少有两条对称轴。
矩形也是中心对称图形,
它的对称中心是对角线的交点。
D
A
B
C
O
矩形的对称性:
既是轴对称图形又是中心对称图形
课堂练习
1、矩形具有而平行四边形不具有的性质( )
A .内角和是360° B .对角相等
C .对边平行且相等 D .对角线相等
2、下面性质中,矩形不一定具有的是( )
A.对角线相等 B .四个角相等
C .是轴对称图形 D .对角线垂直
3、已知矩形的一条对角线与一边的夹角是40°,
则两条对角线所夹锐角的度数为 ( )
A.50° B.60° C.70° D.80°
1.D 2.D 3.D
课堂练习
4、已知:如图,M为 ABCD的AD边上的中点,且MB=MC.
求证: ABCD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
又∵AM=DM,MB=MC,
∴△ABM≌△DCM,
∴∠A=∠D.
∵AB∥CD,
∴∠A+∠D=180°,∴∠A=90°,
∴ ABCD是矩形.
【点悟】证明一个四边形是矩形,可以先证明是平行四边形,再证明有一个角是直角.
5、如图,四边形ABCD是矩形,过A作AE∥BD,交CB的延长线于点E.
(1)猜想:图中的△ACE是_______三角形;
(2)证明你的猜想.
证明:(2)∵四边形ABCD是矩形,
∴AD∥BC,AC=BD.
又∵AE∥BD,∴四边形AEBD是平行四边形,
∴AE=BD,
∴AE=AC,
∴△ACE是等腰三角形.
【点悟】此类探索结论问题,通过分析已知条件,观察图形特征,
得到猜想结论,然后加以证明.
课堂总结
A
B
C
D
矩形特征:
(3)对角线:
四个角都是直角
互相平分
相 等
(2)角:
对边: 平行
相等
(1)边:
(共性)
(共性)
(特性)
(特性)
(特性)
(共性)
邻边:互相垂直
5.1矩形(1)
新知导入
议一议
用6根火柴棒首尾相接摆成一个平行四边形(如图)
思考(1)能摆成多少个不同的平行四边形?它们有什么共同特点?
(2)在这些平行四边形中,有没有面积最大的一个平行四边形?
说出你的理由.
说一说
有一个角是直角的平行四边形叫做矩形。
有一个直角
平行四边形
矩形
矩形是一种特殊的平行四边形。
小学里学过的长方形、正方形都是矩形
矩形还具有哪些特殊的性质呢?
合作探究
矩形还具有哪些特殊的性质呢?
两组对边分别平行且相等
两组对边分别平行且相等
两组对角分别相等
两组对角分别相等
互相平分
互相平分
中心对称图形
中心对称图形
无
四个角都是直角
相等
对称图形轴
新知讲解
提炼概念
矩形性质定理1: 矩形的四个角都是直角.
几何语言:
∵四边形ABCD是矩形,∴∠A=∠B=∠C=∠D=90°
矩形的对角线相等.
这个命题正确吗?试着说说你的理由.
已知:四边形ABCD是矩形.
求证:AC = BD.
证明:在矩形ABCD中,∵∠ABC = ∠DCB = 90°,
又∵AB = DC , BC = CB,
∴△ABC≌△DCB,∴AC = BD.
矩形的性质定理2:矩形的对角线相等.
符号语言:∵四边形ABCD是矩形,∴AC = BD.
归纳概念
典例精讲
新知讲解
例1:已知:如图,在矩形ABCD中对角线AC、BD相交于点O,
∠AOD=120°,AB=4 cm.
(1)判断△AOB的形状;
(2)求矩形对角线的长.
解:(1)∵四边形ABCD是矩形,∴AC=BD,
∴OA=OC=OB=OD,∴OA=OC=OB=OD,∴∠AOB=60°,∴△AOB是等边三角形;
(2)∵AB=4,
∴AC=BD=2AB=8 cm,
即矩形对角线的长为8 cm.
想一想:
矩形是轴对称图形吗?如果是,它有几条对称轴 是中心对称图形吗?
矩形是轴对称图形,它至少有两条对称轴。
矩形也是中心对称图形,
它的对称中心是对角线的交点。
D
A
B
C
O
矩形的对称性:
既是轴对称图形又是中心对称图形
课堂练习
1、矩形具有而平行四边形不具有的性质( )
A .内角和是360° B .对角相等
C .对边平行且相等 D .对角线相等
2、下面性质中,矩形不一定具有的是( )
A.对角线相等 B .四个角相等
C .是轴对称图形 D .对角线垂直
3、已知矩形的一条对角线与一边的夹角是40°,
则两条对角线所夹锐角的度数为 ( )
A.50° B.60° C.70° D.80°
1.D 2.D 3.D
课堂练习
4、已知:如图,M为 ABCD的AD边上的中点,且MB=MC.
求证: ABCD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
又∵AM=DM,MB=MC,
∴△ABM≌△DCM,
∴∠A=∠D.
∵AB∥CD,
∴∠A+∠D=180°,∴∠A=90°,
∴ ABCD是矩形.
【点悟】证明一个四边形是矩形,可以先证明是平行四边形,再证明有一个角是直角.
5、如图,四边形ABCD是矩形,过A作AE∥BD,交CB的延长线于点E.
(1)猜想:图中的△ACE是_______三角形;
(2)证明你的猜想.
证明:(2)∵四边形ABCD是矩形,
∴AD∥BC,AC=BD.
又∵AE∥BD,∴四边形AEBD是平行四边形,
∴AE=BD,
∴AE=AC,
∴△ACE是等腰三角形.
【点悟】此类探索结论问题,通过分析已知条件,观察图形特征,
得到猜想结论,然后加以证明.
课堂总结
A
B
C
D
矩形特征:
(3)对角线:
四个角都是直角
互相平分
相 等
(2)角:
对边: 平行
相等
(1)边:
(共性)
(共性)
(特性)
(特性)
(特性)
(共性)
邻边:互相垂直
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
