第1章 三角形的初步知识1.1-1.5精选习题(含解析)
文档属性
| 名称 | 第1章 三角形的初步知识1.1-1.5精选习题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第1章1.1-1.5各节精选习题(含解析)
一、1.1认识三角形
1.某同学用5cm、7cm、9cm、13cm的四根小木棒摆出不同形状的三角形的个数为( )
A.1 B.2 C.3 D.4
2.用海伦公式求面积的计算方法是: ,其中S表示三角形的面积,a,b,c分别表示三边之长,p表示周长的一半,即 .我国宋代数学家秦九韶提出的“三斜求积术”与这个公式基本一致,所以这个公式也叫“海伦-秦九韶式” .请你利用公式解答下列问题.在 中,已知三边之长 , , ,则 的面积为 .
3.如图,在△ABC中,∠A=70°,∠C=30°,点D为AC边上一点,过点D作DE∥AB,交BC于点E,且DE=BE,则∠BDE的度数是 .
4.在△ABC中,∠B=60°,∠C=40°,AD、AE分别是△ABC的高线和角平分线,则∠DAE的度数为 .
5.先化简,再求值:
,其中a是已知两边分别为2和3的三角形的第三边长,且a是整数.
6.中,CD平分,点E是BC上一动点,连接AE交CD于点D.
(1)如图1,若,AE平分,则的度数为 ;
(2)如图2,若,,,则的度数为 ;
(3)如图3,在BC的右侧过点C作,交AE延长线于点F,且,.试判断AB与CF的位置关系,并证明你的结论.
二、1.2定义与命题
7.下列命题是真命题的个数为( )
①一个角的补角大于这个角.②三角形的内角和是180°.③若
,则
.④相等的角是对顶角.⑤两点之间,线段最短.
A.2 B.3 C.4 D.5
8.下列语句是真命题的是( ).
A.内错角相等
B.若,则
C.直角三角形中,两锐角和的函数关系是一次函数
D.在中,,那么为直角三角形
9.小豪发现一个命题:“如果两个无理数,,满足,那么这两个无理数的和是无理数.”这个命题是 (填写“真命题”,“假命题”);请你举例说明 .
10.命题“两个全等三角形的周长相等”的逆命题是 .
11.探究问题:已知 ,画一个角 ,使 ,且 交 于点 . 与 有怎样的数量关系?
(1)我们发现 与 有两种位置关系:如图1与图2所示.
①图1中 与 数量关系为 ;图2中 与 数量关系为 .请选择其中一种情况说明理由.
②由①得出一个真命题(用文字叙述): .
(2)应用②中的真命题,解决以下问题:若两个角的两边互相平行,且一个角比另一个角的2倍少30°,请直接写出这两个角的度数.
三、1.3证明
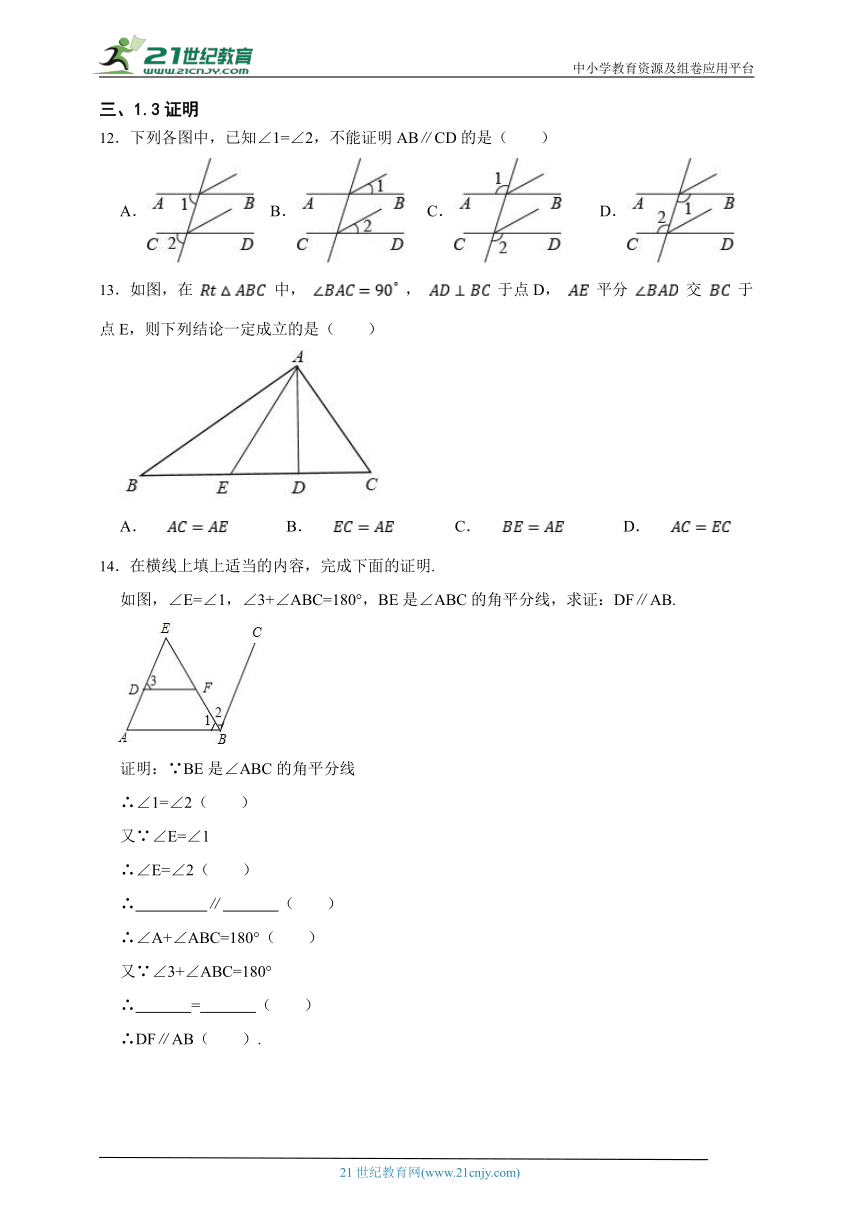
12.下列各图中,已知∠1=∠2,不能证明AB∥CD的是( )
A. B. C. D.
13.如图,在 中, , 于点D, 平分 交 于点E,则下列结论一定成立的是( )
A. B. C. D.
14.在横线上填上适当的内容,完成下面的证明.
如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线,求证:DF∥AB.
证明:∵BE是∠ABC的角平分线
∴∠1=∠2( )
又∵∠E=∠1
∴∠E=∠2( )
∴ ∥ ( )
∴∠A+∠ABC=180°( )
又∵∠3+∠ABC=180°
∴ = ( )
∴DF∥AB( ).
四、1.4全等三角形
15.如图,△ABC≌△ADE,∠C=40°,则∠E的度数为( )
A.80° B.75° C.40° D.70°
16.如图,点D,E,F分别在的边,,上(不与顶点重合),设,.若,则,满足的关系是( )
A. B.
C. D.
17.若,A与D,B与E分别是对应顶点,,,则 .
18.三国时期,数学家赵爽绘制了“勾股圆方图”,又叫“赵爽弦图”,如图所示,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和四边形EFGH都是正方形,如果EF=2,AH=6,那么四边形ABCD的面积等于 .
19.已知:如图,D为△ABC外角∠ACP平分线上一点,且DA=DB,DM⊥BP于点M.
(1)若AC=6,DM=2,求△ACD的面积;
(2)求证:AC=BM+CM.
五、1.5全等三角形的判定
20.如图,三条笔直的公路两两相交,交点分别在点A、B、C处,有两户村民分别在点D和点E处,现准备建造一个蓄水池,要求水池到两条公路AB、BC的距离相等,且到两户村民D、E的距离相等,则水池修建的位置应该是( )
A.在∠B的平分线与DE的交点处
B.在线段AB、AC的垂直平分线的交点处
C.在∠B的平分线与DE的垂直平分线的交点处
D.在∠A的平分线与DE的垂直平分线的交点处
21.如图,在 的网格中,每一个小正方形的边长都是1,点 , , , 都在格点上,连接 , 相交于 ,那么 的大小是( )
A. B. C. D.
22.如图,在 △ABC 中,BE平分 ∠ABC , AE⊥BE 于点E, △BCE 的面积为2,则 △ABC 的面积是 .
23.如图,已知 的周长是22,PB、PC分别平分 和 , 于D,且 , 的面积是 .
24.如图,点D在AC上,BC,DE交于点F, , , .
(1)求证: ;
(2)若 ,求∠CDE的度数.
25.如图,在锐角三角形ABC中,AB=4,△ABC的面积为10,BD平分∠ABC,若M、N分别是BD、BC上的动点,则CM+MN的最小值为
26.直线l经过点A, 在直线l上方, .
(1)如图1, ,过点B,C作直线l的垂线,垂足分别为D、E.求证:
(2)如图2,D,A,E三点在直线l上,若 ( 为任意锐角或钝角),猜想线段DE、BD、CE有何数量关系?并给出证明.
(3)如图3, 过点B作直线l上的垂线,垂足为F,点D是BF延长线上的一个动点,连结AD,作 ,使得 ,连结DE,CE.直线l与CE交于点G.求证:G是CE的中点.
27.在
中,
,
,直线
经过点
,且
于
,
于
.
(1)当直线
绕点
旋转到图1的位置时,
①求证:
≌
;
②求证:
;
(2)当直线
绕点
旋转到图2的位置时,(1)中的结论②还成立吗?若成立,请给出证明;若不成立,说明理由.
六、1.6尺规作图
28.已知下列尺规作图:①作一个角的角平分线;②作一个角等于已知角;③作一条线段的垂直平分线,其中作法正确的是( )
A.①② B.①③ C.②③ D.①②③
29.如图,在中,,以顶点为圆心,适当长为半径画弧,分别交、于点、,再分别以点、为圆心,大于的长为半径画弧,两弧交于点,作射线交于点,若,,则的面积是( )
A.21 B.80 C.40 D.45
30.如图是5×5的正方形网格,△ABC的顶点都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形.画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画出 个.
31.如图,直线a、b、c分别表示相互交叉的马路,要建一个停车场要求到三条马路的距离相等,那么符合条件的修建点有 处.
32.如图,有分别过A、B两个加油站的公路l1、l2相交于点O,现准备在∠AOB内建一个油库,要求油库的位置点P满足到A、B两个加油站的距离相等,而且油库的位置到两条公路l1、l2的距离也相等.那么油库应该修建在什么位置?在图上标出它的位置(不写作法,保留作图痕迹).
33.如图,已知ABC.
(1)请用直尺和圆规作∠ABC的角平分线BD,交AC于点D.(保留作图痕迹,不写作法)
(2)在(1)的条件下,若,,求∠BDA的度数.
七、综合培优
34.已知△ABC的两条中线的长分别为5、10,若第三条中线的长也是整数,则第三条中线长的最大值( )
A.7 B.8 C.14 D.15
35.能说明命题“对于任何实数a,|a|>-a”是假命题的一个反例可以是( )
A.a=-2 B.a= C.a=1 D.a=
36.如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
A. B. C. D.
37.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点 G作EF ∥ BC交AB于E,交AC 于F,过点G作 GD⊥AC 于D,下列四个结论:① EF=BE+CF;②∠BGC=90°+ ∠A ;③点G到 △ABC 各边的距离相等;④设GD=m,AE+AF=n,则 =mn. 其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
38.如图,在△ABC中,∠A=20°,∠ABC与∠ACB的平分线交于点D1,∠ABD1与∠ACD1的平分线交于点D2,以此类推,∠ABD2与∠ACD2的平分线交于点D,则∠BDC的度数是 .
39.如图,在∠AOB 的边
OA、OB 上取点 M、N,连接 MN,P 是△MON 外角平分线的交点,
若 MN=2,S△PMN=2,S△OMN=7.则△MON 的周长是 ;
40.按下列要求画图并填空:
(1)过点B画出直线AC的垂线,交直线AC于点D ,那么点B到直线AC的距离是线段 的长.
(2)用直尺和圆规作出△ABC的边AB的垂直平分线EF,交边AB、AC于点M、N,联结CM .那么线段CM是△ABC的 .(保留作图痕迹)
41.如图1,在△ABC中,BE、CF分别平分∠ABC和∠ACB,BE和CF相交于D点.
(1)求证:∠BDC=90°+;
(2)如图2,若∠A=∠ABE,求证:EB+EC=BC+BF.
42.如图,∠AOB=45°,OC是∠AOB的角平分线,点D是射线OB上的一点,点M为线段OD的中点,过点M作OD的垂线,交射线OA于点E,交射线OC于点F,连接ED,交OC于点G.
(1)依题意补全图形;
(2)猜想EF和EG的数量关系并证明;
(3)求证:ED+EF=2EM.
43.如图(1) , ,BD⊥AB, ,点 在线段 上以 的速度由点 向点 运动,同时,点 在线段 上由点 向点 运动,它们运动的时间为 .
(1)若点 的速度与点 的速度相等,当 时,求证: ;
(2)在(1)的条件下,判断此时 和 的位置关系,并证明;
(3)将图(1)中的“ , ”,改为“ ”,得到图(2),其他条件不变.设点 的运动速度为 ,请问是否存在实数 ,使得 与 全等?若存在,求出相应的 和 的值;若不存在,请说明理由.
答案解析部分
1.【答案】C
【解析】【解答】解:四条木棒的所有组合:5,7,9和5,9,13和5,7,13和7,9,13;
只有5,7,9和5,9,13和7,9,13能组成三角形.
故答案为:C.
【分析】三角形两边之和大于第三边,两边之差小于第三边,据此判断即可.
2.【答案】
【解析】【解答】解:∵三边之长 , , ,
∴ ,
∴ ;
故答案为: .
【分析】 直接利用海伦公式计算即可.
3.【答案】40°
【解析】【解答】解:∵∠A=70°,∠C=30°
∴∠ABC=180° ∠A ∠C=80°
∵DE∥AB
∴∠DEC=∠ABC=80°
∵DE=BE
∴∠BDE=∠DBE
∵∠DEC=∠BDE+∠DBE=2∠BDE
∴
故答案为:40°.
【分析】先利用三角形的内角和求出∠ABC的度数,再根据平行线段的性质可得∠DEC=∠ABC=80°,再利用∠BDE=∠DBE,∠DEC=∠BDE+∠DBE=2∠BDE,即可得到。
4.【答案】10°
【解析】【解答】解:在△ABC中,∠B=60°,∠C=40°,
∴∠BAC=180°-∠B-∠C=180°-40°-60°=80°,
∵AE是的角平分线
∴∠BAE=∠BAC=40°,
∵AD是△ABC的高,
∴∠ADB=90°,
∴在△ADB中,∠BAD=90°-∠B=90°-60°=30°,
∴∠DAE=∠BAE-∠BAD=40°-30°=10°.
故答案为10°
【分析】利用三角形角平分线、中线和高以及角的运算即可得出答案。
5.【答案】解:,
,
,
,
是已知两边分别为2和3的三角形的第三边长,
,即,
为整数,
、3、4,
由分式有意义的条件可知:、2、3,
,
原式.
【解析】【分析】先利用分式的混合运算化简,再求出a的值,最后将a的值代入计算即可。
6.【答案】(1)40°
(2)10°
(3)解:AB∥CF,理由为:
如图,延长AC到G,
∵AC=CF,
∴∠F=∠FAC,
∴∠FCG=∠F+∠FAC=2∠F,
∵CF⊥CD,
∴∠BCF+∠BCD=90°,∠FCG+∠ACD=90°,
∵CD平分∠ACB,
∴∠BCD=∠ACD,
∴∠BCF=∠FCG=2∠F,
∵∠B=2∠F,
∴∠B=∠BCF,
∴AB∥CF.
【解析】【解答】解:(1)∵∠ADC=110°,
∴∠DAC+∠DCA=180°-110°=70°,
∵AE平分∠BAC,CD平分∠ACB,
∴∠BAC=2∠DAC,∠ACB=2∠DCA,
∴∠BAC+∠ACB=2(∠DAC+∠DCA)=140°,
∴∠B=180°-(∠BAC+∠ACB)=180°-140°=40°,
故答案为:40°;
(2)∵∠ADC=∠DCE+∠DEC=100°,∠DCE=53°,
∴∠DEC=100°-53°=47°,
∴∠B+∠BAE=∠DEC=47°,
∵∠B-∠BAE=27°,
∴∠BAE=10°,
故答案为:10°;
【分析】(1)先利用三角形的内角和可得∠DAC+∠DCA=180°-110°=70°,再利用角平分线的定义可得∠BAC+∠ACB=2(∠DAC+∠DCA)=140°,再利用三角形的内角和可得∠B=180°-(∠BAC+∠ACB)=180°-140°=40°;
(2)先利用三角形的外角可得∠DEC=100°-53°=47°,∠B+∠BAE=∠DEC=47°,再结合可求出∠BAE=10°;
(3)延长AC到G,先证明∠FCG=∠F+∠FAC=2∠F,再结合角平分线的定义可得∠BCD=∠ACD,∠BCF=∠FCG=2∠F,再利用等量代换可得∠B=∠BCF,所以AB//CF。
7.【答案】A
【解析】【解答】解:①一个角的补角大于这个角,若这个角是钝角,则其补角小于这个角,原说法错误,假命题;
②三角形的内角和是180°,原说法正确,是真命题;
③若
,则
或
,原说法错误,是假命题;
④相等的角不一定是对顶角,原说法错误,假命题;
⑤两点之间,线段最短,原说法正确,真命题;
综上可得:②⑤是真命题,
故答案为:A.
【分析】根据补角的性质、三角形内角和定理、平方的意义、对顶角和线段的性质分别进行判断即可.
8.【答案】C
【解析】【解答】解:A、两直线平行,内错角相等,故原命题是假命题,不符合题意;
B、若,则,故原命题是假命题,不符合题意;
C、直角三角形中,两锐角和的函数关系是一次函数,故原命题是真命题,符合题意;
D、在中,,那么最大角∠C=,故△ABC为锐三角形,故原命题是假命题,不符合题意;
故答案为:C.
【分析】根据内错角的性质、等式的性质、三角形的内角和逐项判断即可。
9.【答案】假命题;与
【解析】【解答】解:设无理数,则,即
“如果两个无理数,,满足,那么这两个无理数的和是无理数.”是假命题
故答案为:假命题,例如:与(答案不唯一)
【分析】根据无理数的定义和假命题的定义求解即可。
10.【答案】如果两个三角形周长相等,那么这两个三角形全等
【解析】【解答】解:∵原命题的题设为两个全等三角形的周长,结论为三角形周长相等,
所以逆命题是:如果两个三角形的周长相等,那么这两个三角形全等.
【分析】从原命题中找出题设和结论,根据逆命题和原命题的关系直接将题设和条件互换位置后,用如果那么的标准形式写出即可.
11.【答案】(1);;如果两个角的两边互相平行,那么这两个角相等或互补 理由:如图1中, ∵BC∥EF, ∴∠DPB=∠DEF, ∵AB∥DE, ∴∠ABC+∠DPB=180°, ∴∠ABC+∠DEF=180°. 如图2中,∵BC∥EF, ∴∠DPC=∠DEF, ∵AB∥DE, ∴∠ABC=∠DPC, ∴∠ABC=∠DEF.
(2)解:设两个角分别为x和2x-30°,
由题意x=2x-30°或x+2x-30°=180°,
解得x=30°或x=70°,
∴这两个角的度数为30°,30°或70°和110°.
【解析】【分析】(1)①利用平行线的性质逐一进行推导即可得出答案;②根据①中的结论即可得;(2)设两个角分别为x和2x-30°,由题意x=2x-30°或x+2x-30°=180°,解方程即可解决问题.
12.【答案】B
【解析】【解答】:A、∵∠1=∠2,∴AB∥CD,该选项不符合题意;
B、由∠1=∠2,不能判断AB∥CD,该选项符合题意;
C、∵∠1=∠2,∠3=∠2,∴∠1=∠3,∴AB∥CD,该选项不符合题意;
D、∵∠1=∠2,∴AB∥CD,该选项不符合题意;
故答案为:B.
【分析】根据平行线的判定方法逐项判断即可。
13.【答案】D
【解析】【解答】解:∵ ,
∴∠BAE+∠DAE+∠CAD=90°,∠B+∠C=90°
∵AD⊥BC
∴∠BAE+∠DAE+∠B=90°,∠DAE+∠DEA=90°,∠CAD+∠C=90°
∵ 平分
∴∠DAE=∠BAE
∵∠B+∠C=90°
∴∠CAD=∠B
∵∠CEA=∠B+∠BAE
∴∠CEA=∠DAE+∠CAD=∠CAE
∴AC=EC,
其他选项均缺少条件,无法证明一定相等,
故答案为:D.
【分析】利用垂直,角平分线和三角形的外角性质对每个选项一一判断求解即可。
14.【答案】证明:∵BE是∠ABC的角平分线,
∴∠1=∠2(角平分线的定义),
又∵∠E=∠1,
∴∠E=∠2(等量代换),
∴AE∥BC(内错角相等,两直线平行),
∴∠A+∠ABC=180°(两线平行,同旁内角互补),
又∵∠3+∠ABC=180°,
∴∠A=∠3(同角的补角相等),
∴DF∥AB(同位角相等,两直线平行).
【解析】【分析】由角平分线定义,通过角的等量代换可得∠E=∠2,由内错角相等,两直线平行证明AE∥BC,由两直线平行,同旁内角互补得到∠A+∠ABC=180°,再由同角的补角相等得出∠A=∠3,利用同位角相等,两直线平行即可证明DF∥AB,据此填空即可.
15.【答案】C
【解析】【解答】解:∵△ABC≌△ADE,
∴∠E=∠C=40°.
故答案为:C.
【分析】根据全等三角形的性质可得∠E=∠C,据此解答.
16.【答案】B
【解析】【解答】解:∵,
∴∠B=∠C,∠BED=∠EFC,
∵,,在△ABC中,∠A+∠B+∠C=180°,
∴,,
∴,
∵在△EFC中,,
∴,即,
∴.
故答案为:B.
【分析】由全等三角形性质得∠B=∠C,∠BED=∠EFC,由三角形内角和求出,根据平角的定义得,即得,在△EFC中,,从而得出,继而得出结论.
17.【答案】70°
【解析】【解答】解:∵∠A=50°,∠B=60°,
∴∠ACB=180° 50° 60°=70°,
∵△ABC≌△DEF,
∴∠F=∠ACB=70°.
故答案为:70°.
【分析】首先利用内角和定理可得∠ACB的度数,然后根据全等三角形的对应角相等进行解答.
18.【答案】
【解析】【解答】解:∵△ABH≌△BCG,
∴BG=AH=6,
∵四边形EFGH都是正方形,
∴HG=EF=2,
∴BH=8,
在直角三角形AHB中,由勾股定理得到AB2=AH2+BH2=62+82=100,
∴正方形ABCD的面积=100.
故答案为:100.
【分析】由正方形的性质得GH=EF=2,由全等三角形的性质得BG=AH=6,则BH=BG+GH=8,在直角三角形AHB中,由勾股定理得到AB2即可得出答案.
19.【答案】(1)解:作DN⊥AC于点N.
∵D为△ABC外角∠ACP平分线上一点
(2)解:∴在Rt△CDN与Rt△CDM中,
∴在Rt△ADN与Rt△BDM中,
【解析】【分析】(1)作DN⊥AC于点N,根据角平分线性质得DM=DN,再由三角形面积公式即可求得答案.
(2)根据直角三角形全等的判定——HL可得△CDN≌△CDM,△ADN≌△BDM,再由全等三角形性质得CM=CN,AN=BM,等量代换即可得证.
20.【答案】C
【解析】【解答】解:作∠ABC的平分线和DE的垂直平分线,它们相交于P点,如图,
则水池修建的位置应该为P点.
故答案为:C.
【分析】由题意可得点P在∠ABC的角平分线上,且在DE的垂直平分线上,据此解答.
21.【答案】C
【解析】【解答】解:取格点 ,连接 ,
由已知条件可知: ,
∴ ,
∴ ,
同理可得: ,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ 是等腰直角三角形,
∴ ,
即 ,
故答案为:C.
【分析】取格点 ,连接 ,先证明,得出 ,再证明,得出,最后证明 是等腰直角三角形,得出 ,即可得出结论。
22.【答案】4
【解析】【解答】解:延长AE交BC于D,
∵BE平分
,
∴ ,
∵ ,
∴ ,
在
和
中,
,
∴ ,
∴ ,
∴ ,
,
∴
故答案为:4.
【分析】延长AE交BC于D,根据ASA证明
,可得
,根据等底同高可得
,
,从而得出
,即可得解.
23.【答案】33
【解析】【解答】解:如图,连接AP,过点P分别作PE⊥AB于点E,PF⊥AC于点F,
∵PB、PC分别平分
和
,
于D,
∴PD=PE,PD=PF,
∴PD=PE=PF=3,
∵ △ABC的周长是22,
∴ △ABC的面积是
.
故答案为:33.
【分析】连接AP,过点P分别作PE⊥AB于点E,PF⊥AC于点F,由角平分线性质得PD=PE=PF=3,然后根据三角形的面积公式以及面积间的和差关系进行计算.
24.【答案】(1)证明:∵∠ABD=∠CBE,
∴∠ABD+∠DBC=∠CBE+∠DBC,
即:∠ABC=∠DBE,
在△ABC和△DBE中,
,
∴△ABC≌△DBE(SAS);
(2)解:由(1)可知:△ABC≌△DBE,
∴∠C=∠E,
∵∠DFB=∠C+∠CDE,
∠DFB=∠E+∠CBE,
∴∠CDE=∠CBE,
∵∠ABD=∠CBE=20°,
∴∠CDE=20°.
【解析】【分析】(1) 由∠ABD=∠CBE,利用等式的性质求出∠ABC=∠DBE,根据SAS证明△ABC≌△DBE;
(2)由△ABC≌△DBE得∠C=∠E,利用三角形外角的性质得∠DFB=∠C+∠CDE,∠DFB=∠E+∠CBE,从而得出∠CDE=∠CBE=20°.
25.【答案】5
【解析】【解答】解:过点C作CE⊥AB于点E,交BD于点M,过点M作MN⊥BC于N.
∵BD平分∠ABC,ME⊥AB于点E,MN⊥BC于N,
∴MN=ME,
∴CE=CM+ME=CM+MN,
∴CE为CM+MN的最小值.
∵三角形ABC的面积为10,AB=4,
∴4 CE=10,
∴CE.
即CM+MN的最小值为5.
故答案为:5.
【分析】过点C作CE⊥AB于点E,交BD于点M,过点M作MN⊥BC于N,由角平分线的性质可得MN=ME,从而得出CE=CM+ME=CM+MN,继而得出CE为CM+MN的最小值,利用三角形的面积求出CE的长即可.
26.【答案】(1)证明:∵ , ,
∴ ,
∴
∵ ,
∴
∴ ,
在 与 中
,
∴
(2)解:猜想: ,
∵
∴ ,
∴ ,
在 与 中
∴ ,
∴ , ,
∴
(3)证明:分别过点C、E作 , ,
同(1)可证 , ,
∴ ,
∴ ,
∵ , ,
∴
在 与 中
∴ ,
∴ ,
∴G为CE的中点.
【解析】【分析】(1)由垂直的定义可得∠BDA=∠AEC=90°,利用同角的余角相等可得∠ABD=∠CAE,根据AAS证明△ABD≌△CAE;
(2)猜想:DE=BD+CE,理由:根据三角形内角和及平角定义得出∠ABD=∠CAE,根据AAS证明△ABD≌△CAE ,可得BD=AE,DA=EC,从而得出DE=AE+DA=BD+CE;
(3)分别过点C、E作CM⊥l,EN⊥l,利用AAS证△CMG≌△ENG,可得CG=EG,从而得出结论.
27.【答案】(1)证明:①∵AD⊥MN,BE⊥MN,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
又∵AC=BC,
∴ ≌ ;
②∵ ≌ ,
∴CD=BE,AD=CE,
∵DE=CE+CD,
∴DE=AD+BE;
(2)解:DE=AD+BE不成立,此时应有DE=AD-BE,理由如下:
∵BE⊥MN,AD⊥MN,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
又∵AC=BC,
∴ ≌ ,
∴AD=CE,CD=BE,
∵DE=CE-CD,
∴DE=AD-BE.
【解析】【分析】(1)①根据垂直的概念得∠ADC=∠BEC=90°,根据同角的余角相等得∠DAC=∠BCE,然后利用全等三角形的判定定理AAS进行证明;
②根据全等三角形的性质可得CD=BE,AD=CE,然后根据DE=CE+CD进行证明;
(2)同理证明△ADC≌△CEB,得到AD=CE,CD=BE,然后根据DE=CE-CD进行证明.
28.【答案】A
【解析】【解答】解:由作图可知:作图正确的是①②.
故答案为:A.
【分析】利用作一个角等于已知角的方法,作线段垂直平分线的方法,可得答案.
29.【答案】C
【解析】【解答】解:如图,过点D作DH⊥AB于H.
由作图可知,AP平分∠CAB,
∵DC⊥AC,DH⊥AB,
∴DC=DH=5,
∴S△ABD= AB DH=×16×5=40.
故答案为:C.
【分析】过点D作DH⊥AB于H,利用作图可知AP平分∠CAB,利用角平分线上的点到角两边的距离相等,可求出DH的长,再利用三角形的面积公式进行计算,可求出△ABD的面积.
30.【答案】6
【解析】【解答】解:如图:
以BC为公共边可画出△BDC,△BEC,△BFC三个三角形和原三角形全等.
以AB为公共边可画出三个三角形△ABG,△ABM,△ABH和原三角形全等.
所以可画出6个.
故答案为:6.
【分析】根据网格的特点及全等三角形的性质可以以AB和BC为公共边分别画出3个,而AC得不到,从而得出结论.
31.【答案】4
【解析】【解答】解:如图所示,可供选择的地址有4个.
故答案为:4.
【分析】由三角形内角平分线的交点到三角形三边的距离相等,可得三角形内角平分线的交点满足条件;然后利用角平分线的性质,可证得三角形两条外角平分线的交点到其三边的距离也相等,这样的点有3个,可得可供选择的地址有4个.
32.【答案】解:连接 ,作 的垂直平分线,再作 的平分线,
垂直平分线与角平分线的交点即为
P为油库所在地,如图所示.
【解析】【分析】连接 AB ,作 AB 的垂直平分线,再作 的平分线,垂直平分线与角平分线的交点即为油库的所在地.
33.【答案】(1)解:如图
(2)解:∵∠A=100°,∠C=28°,
∴,
又∵BD平分∠ABC,
∴∠DBC=26°,
∴.
【解析】【分析】(1)以点B为圆心,任意长为半径画弧,与AB、BC交于两点,然后分别以这两点为圆心,以大于两点间距离的一半为半径画弧,交于一点,连接该点与点B,并延长,与AC交于点D,则BD为∠ABC的平分线;
(2)根据内角和定理可得∠ABC=52°,根据角平分线的概念可得∠DBC=26°,由外角的性质可得∠BDA=∠DBC+∠C,据此计算.
34.【答案】C
【解析】【解答】如图,角A、B、C对应的中点分别是D、E、F,且三条中线交点是O,将OD延长到G,使OD=DG,连接BG,设BE=5,CF=10,AD则为第三条中线长
∵角A、B、C对应的中点分别是D、E、F,且三条中线交点是O
∴ ,
∵OD=DG
∴
∴
∴
∴
∵第三条中线的长也是整数
∴第三条中线长的最大值为14
故答案为:C.
【分析】如图,角A、B、C对应的中点分别是D、E、F,且三条中线交点是O,将OD延长到G,使OD=DG,连接BG,设BE=5,CF=10,AD则为第三条中线长,根据三角形的三边关系和中线的性质列出不等式组,即可求出第三条中线长的最大值.
35.【答案】A
【解析】【解答】A、∵=2=-(-2),∴|a|>-a,错误,符合题意;
B、=>-, 正确,不符合题意;
C、=1>-1, 正确,不符合题意;
D、=-,正确,不符合题意;
故答案为:A.
【分析】当a>0时,|a|>-a,当a≤0时,|a|=-a,据此逐项分析即可判断.
36.【答案】D
【解析】【解答】∵PB+PC=BC,
而PA+PC=BC,
∴PA=PB,
∴点P在AB的垂直平分线上,
即点P为AB的垂直平分线与BC的交点.
故选D.
【分析】由PB+PC=BC和PA+PC=BC易得PA=PB,根据线段垂直平分线定理的逆定理可得点P在AB的垂直平分线上,于是可判断D选项正确.
37.【答案】C
【解析】【解答】解: ① ∵EF∥BC,∴∠EGB=∠CBG,∵∠EBG=CBG,∴∠EBG=∠EGB,∴EB=EG,同理FC=FG,EF=EG+FG=BE+CF,正确;
②∵BG和CG分别是∠ABC和∠ACB的平分线,∴∠CBG=∠ABC,∠BCG=∠ACB,∠BGC=180°-∠CBG-∠BCG=180°-(∠ABC+∠ACB)=180°-(180°-∠A)=90°+ ∠A ,正确;
③如图,过G作GN⊥AB,GM⊥BC,
∵BG是∠ABC的平分线,∴GN=GM,∵CG是∠ACB的平分线,∴GM=GD,∴GM=GN=GD,即
点G到 △ABC 各边的距离相等,正确;
④如图,连接AG,
S△AEF=S△AEG+S△AFG=AE×GN+AF×GD=(AE+AF)×GD=mn,错误.
综上,正确的有3项.
故答案为:C.
【分析】利用角的平分线和过平分线的一点作角的一边的平行线可得等腰三角形,推出EF等于BE和CF之和;根据角平分线的性质,结合三角形内角和定理把∠BGC用∠ABC和∠ACB表示,从而可把∠BGC用含∠A的关系式表示;因为G是三角形两角平分线的交点,根据角平分线性质定理可得点G到三角形的三边距离相等;用分割法求三角形面积,可得△AEF的面积是mn.
38.【答案】40°
【解析】【解答】∵∠A=20°,∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=160°,
∵BD1平分∠ABC,CD1平分∠ACB,
∴∠ABD1= ∠ABC,∠ACD1= ∠ACD,
∵BD2平分∠ABD1,CD2平分∠ACD1,
∴∠ABD2= ∠ABD1= ∠ABC,∠ACD2= ∠ACD1= ∠ACB,
同理可得∠ABD= ∠ABC,∠ACD= ∠ACB,
∴∠ABD+∠ACD=160°× =20°,
∴∠BCD+∠CBD=140°
∴∠BDC=180﹣∠BCD﹣∠CBD=40°
故答案为40°.
【分析】根据题意可得∠ABC+∠ACB=160°,BD1,CD1,CD2,BD2…BDn,CDn是角平分线,可得∠ABDn+∠ACDn=160×( )n,可求∠BCDn+∠CBDn的值,再根据三角形内角和定理可求结果.
39.【答案】11
【解析】【解答】解:如图:作PE⊥OB,PG⊥OA,PF⊥MN,连结OP,
∵PM、PN分别平分∠AMN,∠BNM,
∴PF=PG=PE,
∵S△PMN=·MN·PF=2,MN=2,
∴PF=PG=PE=2,
由题易得:
△GMP≌△GFP,△FPN≌△EPN,△OPG≌△OEP,
∴GM=GF,FN=NE,OG=OE,
∴S△OPG=S△OPE=×(2+2+7)=,
即S△OPG=·OG·PG=,
∴OG=,
∴C△MON=OM+ON+MN,
=OM+ON+MF+FN,
=OM+ON+MG+NE,
=OG+OE,
=2OG,
=2×,
=11.
故答案为:11.
【分析】作PE⊥OB,PG⊥OA,PF⊥MN,连结OP,根据角平分线的性质定理得PF=PG=PE,再由三角形面积公式得PF=PG=PE=2,据条件易得:△GMP≌△GFP,△FPN≌△EPN,△OPG≌△OEP,由全等三角形性质得GM=GF,FN=NE,OG=OE,S△OPG=·OG·PG=得OG=,由三角形周长和等量代换可得答案.
40.【答案】(1);BD
(2);边AB的中线
【解析】【解答】(1)如图所示,BD为所求作的垂线,点B到直线AC的距离是线段BD的长度,
故答案为:BD;(2)如图所示,EF为所求作的线段AB的垂直平分线,
线段CM是△ABC的边AB的中线,
故答案为:边AB的中线.
【分析】(1)以点B为圆心,以任意长为半径画弧,与AC的延长线相交于两点,在以这两点为圆心,以大于它们距离的一半为半径画弧,两弧相交于一点,连接点B与这一点与AC的延长线相交于点D,则点D即为所求,根据点到直线的距离解答;(2)分别以点A、B为圆心,以大于 AB为半径画弧,两弧相交于两点,过这两点作直线EF即可,根据线段垂直平分线的定义可得点M是AB的中点,然后根据中线的定义解答.
41.【答案】(1)证明:、分别平分和,
,
,
,
;
(2)证明:,
,
,
如图,过点作,交于点,
,
,
,,
在和中,,
,
,
,
.
【解析】【分析】(1)利用角平分线和三角形的内角和计算求解即可;
(2)先求出AE=EB,再利用全等三角形的判定与性质求解即可。
42.【答案】(1)解:根据题意,如图:
(2)解:EF=EG;
理由如下:如图,
∵点M为线段OD的中点,EM⊥OD,
∴线段EM是△OED的高,也是中线,
∴EM垂直平分OD,∠OME=90°,
∴OE=DE,
∴∠EDO=∠AOB=∠OEF=45°,
∵OC是∠AOB的角平分线,
∴∠AOC=∠BOC,
∴∠AOC+∠OEF=∠BOC+∠EDO,
∴∠EFG=∠EGF,
∴EF=EG;
(3)解:在射线EA上,截取EH=EG,连接GH,如图:
则EH=EF,
∵OE=DE,
∴ED+EF=OE+EH=OH,
∵∠EDO=∠EOM=∠OEF=45°,点M是OD的中点,
∴OM=EM=DM,∠DEA=45°+45°=90°,
∴OD=2EM;∠EHG=45°,
∵∠AOC=∠BOC,OG=OG,
∴△ODG≌△OHG(AAS),
∴OD=OH,
∴ED+EF=2EM.
【解析】【分析】(1)根据要求画出图形即可;
(2)结论:EF=EG,欲证明EF=EG,只要证明∠EFG=∠EGF=67.5°即可;
(3)过点G作OD的垂线,垂足为N,证明GN=EG=EF,ON=OE=ED,可得结论。
43.【答案】(1)解: 与 全等,
理由如下:当 时, ,
则 ,
∴ ,
又∵ ,
在 和 中,
∴ ;
(2)解: ,
证明:∵ ,
∴ ,
∴ .
∴ ,
即 ;
(3)解: , ,
①若
则 , ,
∴ ,
解得: ,则 ;
②若 ,
则 , ,
则 ,解得, ,
∴ ,解得, ,
故当 , 或 , 时, 与 全等.
【解析】【分析】(1)当t=1时求得 ,再利用SAS即可证明 ;(2)根据 ,推出 ,即可证明 ;(3)分 及 两种情况判断即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第1章1.1-1.5各节精选习题(含解析)
一、1.1认识三角形
1.某同学用5cm、7cm、9cm、13cm的四根小木棒摆出不同形状的三角形的个数为( )
A.1 B.2 C.3 D.4
2.用海伦公式求面积的计算方法是: ,其中S表示三角形的面积,a,b,c分别表示三边之长,p表示周长的一半,即 .我国宋代数学家秦九韶提出的“三斜求积术”与这个公式基本一致,所以这个公式也叫“海伦-秦九韶式” .请你利用公式解答下列问题.在 中,已知三边之长 , , ,则 的面积为 .
3.如图,在△ABC中,∠A=70°,∠C=30°,点D为AC边上一点,过点D作DE∥AB,交BC于点E,且DE=BE,则∠BDE的度数是 .
4.在△ABC中,∠B=60°,∠C=40°,AD、AE分别是△ABC的高线和角平分线,则∠DAE的度数为 .
5.先化简,再求值:
,其中a是已知两边分别为2和3的三角形的第三边长,且a是整数.
6.中,CD平分,点E是BC上一动点,连接AE交CD于点D.
(1)如图1,若,AE平分,则的度数为 ;
(2)如图2,若,,,则的度数为 ;
(3)如图3,在BC的右侧过点C作,交AE延长线于点F,且,.试判断AB与CF的位置关系,并证明你的结论.
二、1.2定义与命题
7.下列命题是真命题的个数为( )
①一个角的补角大于这个角.②三角形的内角和是180°.③若
,则
.④相等的角是对顶角.⑤两点之间,线段最短.
A.2 B.3 C.4 D.5
8.下列语句是真命题的是( ).
A.内错角相等
B.若,则
C.直角三角形中,两锐角和的函数关系是一次函数
D.在中,,那么为直角三角形
9.小豪发现一个命题:“如果两个无理数,,满足,那么这两个无理数的和是无理数.”这个命题是 (填写“真命题”,“假命题”);请你举例说明 .
10.命题“两个全等三角形的周长相等”的逆命题是 .
11.探究问题:已知 ,画一个角 ,使 ,且 交 于点 . 与 有怎样的数量关系?
(1)我们发现 与 有两种位置关系:如图1与图2所示.
①图1中 与 数量关系为 ;图2中 与 数量关系为 .请选择其中一种情况说明理由.
②由①得出一个真命题(用文字叙述): .
(2)应用②中的真命题,解决以下问题:若两个角的两边互相平行,且一个角比另一个角的2倍少30°,请直接写出这两个角的度数.
三、1.3证明
12.下列各图中,已知∠1=∠2,不能证明AB∥CD的是( )
A. B. C. D.
13.如图,在 中, , 于点D, 平分 交 于点E,则下列结论一定成立的是( )
A. B. C. D.
14.在横线上填上适当的内容,完成下面的证明.
如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线,求证:DF∥AB.
证明:∵BE是∠ABC的角平分线
∴∠1=∠2( )
又∵∠E=∠1
∴∠E=∠2( )
∴ ∥ ( )
∴∠A+∠ABC=180°( )
又∵∠3+∠ABC=180°
∴ = ( )
∴DF∥AB( ).
四、1.4全等三角形
15.如图,△ABC≌△ADE,∠C=40°,则∠E的度数为( )
A.80° B.75° C.40° D.70°
16.如图,点D,E,F分别在的边,,上(不与顶点重合),设,.若,则,满足的关系是( )
A. B.
C. D.
17.若,A与D,B与E分别是对应顶点,,,则 .
18.三国时期,数学家赵爽绘制了“勾股圆方图”,又叫“赵爽弦图”,如图所示,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和四边形EFGH都是正方形,如果EF=2,AH=6,那么四边形ABCD的面积等于 .
19.已知:如图,D为△ABC外角∠ACP平分线上一点,且DA=DB,DM⊥BP于点M.
(1)若AC=6,DM=2,求△ACD的面积;
(2)求证:AC=BM+CM.
五、1.5全等三角形的判定
20.如图,三条笔直的公路两两相交,交点分别在点A、B、C处,有两户村民分别在点D和点E处,现准备建造一个蓄水池,要求水池到两条公路AB、BC的距离相等,且到两户村民D、E的距离相等,则水池修建的位置应该是( )
A.在∠B的平分线与DE的交点处
B.在线段AB、AC的垂直平分线的交点处
C.在∠B的平分线与DE的垂直平分线的交点处
D.在∠A的平分线与DE的垂直平分线的交点处
21.如图,在 的网格中,每一个小正方形的边长都是1,点 , , , 都在格点上,连接 , 相交于 ,那么 的大小是( )
A. B. C. D.
22.如图,在 △ABC 中,BE平分 ∠ABC , AE⊥BE 于点E, △BCE 的面积为2,则 △ABC 的面积是 .
23.如图,已知 的周长是22,PB、PC分别平分 和 , 于D,且 , 的面积是 .
24.如图,点D在AC上,BC,DE交于点F, , , .
(1)求证: ;
(2)若 ,求∠CDE的度数.
25.如图,在锐角三角形ABC中,AB=4,△ABC的面积为10,BD平分∠ABC,若M、N分别是BD、BC上的动点,则CM+MN的最小值为
26.直线l经过点A, 在直线l上方, .
(1)如图1, ,过点B,C作直线l的垂线,垂足分别为D、E.求证:
(2)如图2,D,A,E三点在直线l上,若 ( 为任意锐角或钝角),猜想线段DE、BD、CE有何数量关系?并给出证明.
(3)如图3, 过点B作直线l上的垂线,垂足为F,点D是BF延长线上的一个动点,连结AD,作 ,使得 ,连结DE,CE.直线l与CE交于点G.求证:G是CE的中点.
27.在
中,
,
,直线
经过点
,且
于
,
于
.
(1)当直线
绕点
旋转到图1的位置时,
①求证:
≌
;
②求证:
;
(2)当直线
绕点
旋转到图2的位置时,(1)中的结论②还成立吗?若成立,请给出证明;若不成立,说明理由.
六、1.6尺规作图
28.已知下列尺规作图:①作一个角的角平分线;②作一个角等于已知角;③作一条线段的垂直平分线,其中作法正确的是( )
A.①② B.①③ C.②③ D.①②③
29.如图,在中,,以顶点为圆心,适当长为半径画弧,分别交、于点、,再分别以点、为圆心,大于的长为半径画弧,两弧交于点,作射线交于点,若,,则的面积是( )
A.21 B.80 C.40 D.45
30.如图是5×5的正方形网格,△ABC的顶点都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形.画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画出 个.
31.如图,直线a、b、c分别表示相互交叉的马路,要建一个停车场要求到三条马路的距离相等,那么符合条件的修建点有 处.
32.如图,有分别过A、B两个加油站的公路l1、l2相交于点O,现准备在∠AOB内建一个油库,要求油库的位置点P满足到A、B两个加油站的距离相等,而且油库的位置到两条公路l1、l2的距离也相等.那么油库应该修建在什么位置?在图上标出它的位置(不写作法,保留作图痕迹).
33.如图,已知ABC.
(1)请用直尺和圆规作∠ABC的角平分线BD,交AC于点D.(保留作图痕迹,不写作法)
(2)在(1)的条件下,若,,求∠BDA的度数.
七、综合培优
34.已知△ABC的两条中线的长分别为5、10,若第三条中线的长也是整数,则第三条中线长的最大值( )
A.7 B.8 C.14 D.15
35.能说明命题“对于任何实数a,|a|>-a”是假命题的一个反例可以是( )
A.a=-2 B.a= C.a=1 D.a=
36.如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
A. B. C. D.
37.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点 G作EF ∥ BC交AB于E,交AC 于F,过点G作 GD⊥AC 于D,下列四个结论:① EF=BE+CF;②∠BGC=90°+ ∠A ;③点G到 △ABC 各边的距离相等;④设GD=m,AE+AF=n,则 =mn. 其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
38.如图,在△ABC中,∠A=20°,∠ABC与∠ACB的平分线交于点D1,∠ABD1与∠ACD1的平分线交于点D2,以此类推,∠ABD2与∠ACD2的平分线交于点D,则∠BDC的度数是 .
39.如图,在∠AOB 的边
OA、OB 上取点 M、N,连接 MN,P 是△MON 外角平分线的交点,
若 MN=2,S△PMN=2,S△OMN=7.则△MON 的周长是 ;
40.按下列要求画图并填空:
(1)过点B画出直线AC的垂线,交直线AC于点D ,那么点B到直线AC的距离是线段 的长.
(2)用直尺和圆规作出△ABC的边AB的垂直平分线EF,交边AB、AC于点M、N,联结CM .那么线段CM是△ABC的 .(保留作图痕迹)
41.如图1,在△ABC中,BE、CF分别平分∠ABC和∠ACB,BE和CF相交于D点.
(1)求证:∠BDC=90°+;
(2)如图2,若∠A=∠ABE,求证:EB+EC=BC+BF.
42.如图,∠AOB=45°,OC是∠AOB的角平分线,点D是射线OB上的一点,点M为线段OD的中点,过点M作OD的垂线,交射线OA于点E,交射线OC于点F,连接ED,交OC于点G.
(1)依题意补全图形;
(2)猜想EF和EG的数量关系并证明;
(3)求证:ED+EF=2EM.
43.如图(1) , ,BD⊥AB, ,点 在线段 上以 的速度由点 向点 运动,同时,点 在线段 上由点 向点 运动,它们运动的时间为 .
(1)若点 的速度与点 的速度相等,当 时,求证: ;
(2)在(1)的条件下,判断此时 和 的位置关系,并证明;
(3)将图(1)中的“ , ”,改为“ ”,得到图(2),其他条件不变.设点 的运动速度为 ,请问是否存在实数 ,使得 与 全等?若存在,求出相应的 和 的值;若不存在,请说明理由.
答案解析部分
1.【答案】C
【解析】【解答】解:四条木棒的所有组合:5,7,9和5,9,13和5,7,13和7,9,13;
只有5,7,9和5,9,13和7,9,13能组成三角形.
故答案为:C.
【分析】三角形两边之和大于第三边,两边之差小于第三边,据此判断即可.
2.【答案】
【解析】【解答】解:∵三边之长 , , ,
∴ ,
∴ ;
故答案为: .
【分析】 直接利用海伦公式计算即可.
3.【答案】40°
【解析】【解答】解:∵∠A=70°,∠C=30°
∴∠ABC=180° ∠A ∠C=80°
∵DE∥AB
∴∠DEC=∠ABC=80°
∵DE=BE
∴∠BDE=∠DBE
∵∠DEC=∠BDE+∠DBE=2∠BDE
∴
故答案为:40°.
【分析】先利用三角形的内角和求出∠ABC的度数,再根据平行线段的性质可得∠DEC=∠ABC=80°,再利用∠BDE=∠DBE,∠DEC=∠BDE+∠DBE=2∠BDE,即可得到。
4.【答案】10°
【解析】【解答】解:在△ABC中,∠B=60°,∠C=40°,
∴∠BAC=180°-∠B-∠C=180°-40°-60°=80°,
∵AE是的角平分线
∴∠BAE=∠BAC=40°,
∵AD是△ABC的高,
∴∠ADB=90°,
∴在△ADB中,∠BAD=90°-∠B=90°-60°=30°,
∴∠DAE=∠BAE-∠BAD=40°-30°=10°.
故答案为10°
【分析】利用三角形角平分线、中线和高以及角的运算即可得出答案。
5.【答案】解:,
,
,
,
是已知两边分别为2和3的三角形的第三边长,
,即,
为整数,
、3、4,
由分式有意义的条件可知:、2、3,
,
原式.
【解析】【分析】先利用分式的混合运算化简,再求出a的值,最后将a的值代入计算即可。
6.【答案】(1)40°
(2)10°
(3)解:AB∥CF,理由为:
如图,延长AC到G,
∵AC=CF,
∴∠F=∠FAC,
∴∠FCG=∠F+∠FAC=2∠F,
∵CF⊥CD,
∴∠BCF+∠BCD=90°,∠FCG+∠ACD=90°,
∵CD平分∠ACB,
∴∠BCD=∠ACD,
∴∠BCF=∠FCG=2∠F,
∵∠B=2∠F,
∴∠B=∠BCF,
∴AB∥CF.
【解析】【解答】解:(1)∵∠ADC=110°,
∴∠DAC+∠DCA=180°-110°=70°,
∵AE平分∠BAC,CD平分∠ACB,
∴∠BAC=2∠DAC,∠ACB=2∠DCA,
∴∠BAC+∠ACB=2(∠DAC+∠DCA)=140°,
∴∠B=180°-(∠BAC+∠ACB)=180°-140°=40°,
故答案为:40°;
(2)∵∠ADC=∠DCE+∠DEC=100°,∠DCE=53°,
∴∠DEC=100°-53°=47°,
∴∠B+∠BAE=∠DEC=47°,
∵∠B-∠BAE=27°,
∴∠BAE=10°,
故答案为:10°;
【分析】(1)先利用三角形的内角和可得∠DAC+∠DCA=180°-110°=70°,再利用角平分线的定义可得∠BAC+∠ACB=2(∠DAC+∠DCA)=140°,再利用三角形的内角和可得∠B=180°-(∠BAC+∠ACB)=180°-140°=40°;
(2)先利用三角形的外角可得∠DEC=100°-53°=47°,∠B+∠BAE=∠DEC=47°,再结合可求出∠BAE=10°;
(3)延长AC到G,先证明∠FCG=∠F+∠FAC=2∠F,再结合角平分线的定义可得∠BCD=∠ACD,∠BCF=∠FCG=2∠F,再利用等量代换可得∠B=∠BCF,所以AB//CF。
7.【答案】A
【解析】【解答】解:①一个角的补角大于这个角,若这个角是钝角,则其补角小于这个角,原说法错误,假命题;
②三角形的内角和是180°,原说法正确,是真命题;
③若
,则
或
,原说法错误,是假命题;
④相等的角不一定是对顶角,原说法错误,假命题;
⑤两点之间,线段最短,原说法正确,真命题;
综上可得:②⑤是真命题,
故答案为:A.
【分析】根据补角的性质、三角形内角和定理、平方的意义、对顶角和线段的性质分别进行判断即可.
8.【答案】C
【解析】【解答】解:A、两直线平行,内错角相等,故原命题是假命题,不符合题意;
B、若,则,故原命题是假命题,不符合题意;
C、直角三角形中,两锐角和的函数关系是一次函数,故原命题是真命题,符合题意;
D、在中,,那么最大角∠C=,故△ABC为锐三角形,故原命题是假命题,不符合题意;
故答案为:C.
【分析】根据内错角的性质、等式的性质、三角形的内角和逐项判断即可。
9.【答案】假命题;与
【解析】【解答】解:设无理数,则,即
“如果两个无理数,,满足,那么这两个无理数的和是无理数.”是假命题
故答案为:假命题,例如:与(答案不唯一)
【分析】根据无理数的定义和假命题的定义求解即可。
10.【答案】如果两个三角形周长相等,那么这两个三角形全等
【解析】【解答】解:∵原命题的题设为两个全等三角形的周长,结论为三角形周长相等,
所以逆命题是:如果两个三角形的周长相等,那么这两个三角形全等.
【分析】从原命题中找出题设和结论,根据逆命题和原命题的关系直接将题设和条件互换位置后,用如果那么的标准形式写出即可.
11.【答案】(1);;如果两个角的两边互相平行,那么这两个角相等或互补 理由:如图1中, ∵BC∥EF, ∴∠DPB=∠DEF, ∵AB∥DE, ∴∠ABC+∠DPB=180°, ∴∠ABC+∠DEF=180°. 如图2中,∵BC∥EF, ∴∠DPC=∠DEF, ∵AB∥DE, ∴∠ABC=∠DPC, ∴∠ABC=∠DEF.
(2)解:设两个角分别为x和2x-30°,
由题意x=2x-30°或x+2x-30°=180°,
解得x=30°或x=70°,
∴这两个角的度数为30°,30°或70°和110°.
【解析】【分析】(1)①利用平行线的性质逐一进行推导即可得出答案;②根据①中的结论即可得;(2)设两个角分别为x和2x-30°,由题意x=2x-30°或x+2x-30°=180°,解方程即可解决问题.
12.【答案】B
【解析】【解答】:A、∵∠1=∠2,∴AB∥CD,该选项不符合题意;
B、由∠1=∠2,不能判断AB∥CD,该选项符合题意;
C、∵∠1=∠2,∠3=∠2,∴∠1=∠3,∴AB∥CD,该选项不符合题意;
D、∵∠1=∠2,∴AB∥CD,该选项不符合题意;
故答案为:B.
【分析】根据平行线的判定方法逐项判断即可。
13.【答案】D
【解析】【解答】解:∵ ,
∴∠BAE+∠DAE+∠CAD=90°,∠B+∠C=90°
∵AD⊥BC
∴∠BAE+∠DAE+∠B=90°,∠DAE+∠DEA=90°,∠CAD+∠C=90°
∵ 平分
∴∠DAE=∠BAE
∵∠B+∠C=90°
∴∠CAD=∠B
∵∠CEA=∠B+∠BAE
∴∠CEA=∠DAE+∠CAD=∠CAE
∴AC=EC,
其他选项均缺少条件,无法证明一定相等,
故答案为:D.
【分析】利用垂直,角平分线和三角形的外角性质对每个选项一一判断求解即可。
14.【答案】证明:∵BE是∠ABC的角平分线,
∴∠1=∠2(角平分线的定义),
又∵∠E=∠1,
∴∠E=∠2(等量代换),
∴AE∥BC(内错角相等,两直线平行),
∴∠A+∠ABC=180°(两线平行,同旁内角互补),
又∵∠3+∠ABC=180°,
∴∠A=∠3(同角的补角相等),
∴DF∥AB(同位角相等,两直线平行).
【解析】【分析】由角平分线定义,通过角的等量代换可得∠E=∠2,由内错角相等,两直线平行证明AE∥BC,由两直线平行,同旁内角互补得到∠A+∠ABC=180°,再由同角的补角相等得出∠A=∠3,利用同位角相等,两直线平行即可证明DF∥AB,据此填空即可.
15.【答案】C
【解析】【解答】解:∵△ABC≌△ADE,
∴∠E=∠C=40°.
故答案为:C.
【分析】根据全等三角形的性质可得∠E=∠C,据此解答.
16.【答案】B
【解析】【解答】解:∵,
∴∠B=∠C,∠BED=∠EFC,
∵,,在△ABC中,∠A+∠B+∠C=180°,
∴,,
∴,
∵在△EFC中,,
∴,即,
∴.
故答案为:B.
【分析】由全等三角形性质得∠B=∠C,∠BED=∠EFC,由三角形内角和求出,根据平角的定义得,即得,在△EFC中,,从而得出,继而得出结论.
17.【答案】70°
【解析】【解答】解:∵∠A=50°,∠B=60°,
∴∠ACB=180° 50° 60°=70°,
∵△ABC≌△DEF,
∴∠F=∠ACB=70°.
故答案为:70°.
【分析】首先利用内角和定理可得∠ACB的度数,然后根据全等三角形的对应角相等进行解答.
18.【答案】
【解析】【解答】解:∵△ABH≌△BCG,
∴BG=AH=6,
∵四边形EFGH都是正方形,
∴HG=EF=2,
∴BH=8,
在直角三角形AHB中,由勾股定理得到AB2=AH2+BH2=62+82=100,
∴正方形ABCD的面积=100.
故答案为:100.
【分析】由正方形的性质得GH=EF=2,由全等三角形的性质得BG=AH=6,则BH=BG+GH=8,在直角三角形AHB中,由勾股定理得到AB2即可得出答案.
19.【答案】(1)解:作DN⊥AC于点N.
∵D为△ABC外角∠ACP平分线上一点
(2)解:∴在Rt△CDN与Rt△CDM中,
∴在Rt△ADN与Rt△BDM中,
【解析】【分析】(1)作DN⊥AC于点N,根据角平分线性质得DM=DN,再由三角形面积公式即可求得答案.
(2)根据直角三角形全等的判定——HL可得△CDN≌△CDM,△ADN≌△BDM,再由全等三角形性质得CM=CN,AN=BM,等量代换即可得证.
20.【答案】C
【解析】【解答】解:作∠ABC的平分线和DE的垂直平分线,它们相交于P点,如图,
则水池修建的位置应该为P点.
故答案为:C.
【分析】由题意可得点P在∠ABC的角平分线上,且在DE的垂直平分线上,据此解答.
21.【答案】C
【解析】【解答】解:取格点 ,连接 ,
由已知条件可知: ,
∴ ,
∴ ,
同理可得: ,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ 是等腰直角三角形,
∴ ,
即 ,
故答案为:C.
【分析】取格点 ,连接 ,先证明,得出 ,再证明,得出,最后证明 是等腰直角三角形,得出 ,即可得出结论。
22.【答案】4
【解析】【解答】解:延长AE交BC于D,
∵BE平分
,
∴ ,
∵ ,
∴ ,
在
和
中,
,
∴ ,
∴ ,
∴ ,
,
∴
故答案为:4.
【分析】延长AE交BC于D,根据ASA证明
,可得
,根据等底同高可得
,
,从而得出
,即可得解.
23.【答案】33
【解析】【解答】解:如图,连接AP,过点P分别作PE⊥AB于点E,PF⊥AC于点F,
∵PB、PC分别平分
和
,
于D,
∴PD=PE,PD=PF,
∴PD=PE=PF=3,
∵ △ABC的周长是22,
∴ △ABC的面积是
.
故答案为:33.
【分析】连接AP,过点P分别作PE⊥AB于点E,PF⊥AC于点F,由角平分线性质得PD=PE=PF=3,然后根据三角形的面积公式以及面积间的和差关系进行计算.
24.【答案】(1)证明:∵∠ABD=∠CBE,
∴∠ABD+∠DBC=∠CBE+∠DBC,
即:∠ABC=∠DBE,
在△ABC和△DBE中,
,
∴△ABC≌△DBE(SAS);
(2)解:由(1)可知:△ABC≌△DBE,
∴∠C=∠E,
∵∠DFB=∠C+∠CDE,
∠DFB=∠E+∠CBE,
∴∠CDE=∠CBE,
∵∠ABD=∠CBE=20°,
∴∠CDE=20°.
【解析】【分析】(1) 由∠ABD=∠CBE,利用等式的性质求出∠ABC=∠DBE,根据SAS证明△ABC≌△DBE;
(2)由△ABC≌△DBE得∠C=∠E,利用三角形外角的性质得∠DFB=∠C+∠CDE,∠DFB=∠E+∠CBE,从而得出∠CDE=∠CBE=20°.
25.【答案】5
【解析】【解答】解:过点C作CE⊥AB于点E,交BD于点M,过点M作MN⊥BC于N.
∵BD平分∠ABC,ME⊥AB于点E,MN⊥BC于N,
∴MN=ME,
∴CE=CM+ME=CM+MN,
∴CE为CM+MN的最小值.
∵三角形ABC的面积为10,AB=4,
∴4 CE=10,
∴CE.
即CM+MN的最小值为5.
故答案为:5.
【分析】过点C作CE⊥AB于点E,交BD于点M,过点M作MN⊥BC于N,由角平分线的性质可得MN=ME,从而得出CE=CM+ME=CM+MN,继而得出CE为CM+MN的最小值,利用三角形的面积求出CE的长即可.
26.【答案】(1)证明:∵ , ,
∴ ,
∴
∵ ,
∴
∴ ,
在 与 中
,
∴
(2)解:猜想: ,
∵
∴ ,
∴ ,
在 与 中
∴ ,
∴ , ,
∴
(3)证明:分别过点C、E作 , ,
同(1)可证 , ,
∴ ,
∴ ,
∵ , ,
∴
在 与 中
∴ ,
∴ ,
∴G为CE的中点.
【解析】【分析】(1)由垂直的定义可得∠BDA=∠AEC=90°,利用同角的余角相等可得∠ABD=∠CAE,根据AAS证明△ABD≌△CAE;
(2)猜想:DE=BD+CE,理由:根据三角形内角和及平角定义得出∠ABD=∠CAE,根据AAS证明△ABD≌△CAE ,可得BD=AE,DA=EC,从而得出DE=AE+DA=BD+CE;
(3)分别过点C、E作CM⊥l,EN⊥l,利用AAS证△CMG≌△ENG,可得CG=EG,从而得出结论.
27.【答案】(1)证明:①∵AD⊥MN,BE⊥MN,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
又∵AC=BC,
∴ ≌ ;
②∵ ≌ ,
∴CD=BE,AD=CE,
∵DE=CE+CD,
∴DE=AD+BE;
(2)解:DE=AD+BE不成立,此时应有DE=AD-BE,理由如下:
∵BE⊥MN,AD⊥MN,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
又∵AC=BC,
∴ ≌ ,
∴AD=CE,CD=BE,
∵DE=CE-CD,
∴DE=AD-BE.
【解析】【分析】(1)①根据垂直的概念得∠ADC=∠BEC=90°,根据同角的余角相等得∠DAC=∠BCE,然后利用全等三角形的判定定理AAS进行证明;
②根据全等三角形的性质可得CD=BE,AD=CE,然后根据DE=CE+CD进行证明;
(2)同理证明△ADC≌△CEB,得到AD=CE,CD=BE,然后根据DE=CE-CD进行证明.
28.【答案】A
【解析】【解答】解:由作图可知:作图正确的是①②.
故答案为:A.
【分析】利用作一个角等于已知角的方法,作线段垂直平分线的方法,可得答案.
29.【答案】C
【解析】【解答】解:如图,过点D作DH⊥AB于H.
由作图可知,AP平分∠CAB,
∵DC⊥AC,DH⊥AB,
∴DC=DH=5,
∴S△ABD= AB DH=×16×5=40.
故答案为:C.
【分析】过点D作DH⊥AB于H,利用作图可知AP平分∠CAB,利用角平分线上的点到角两边的距离相等,可求出DH的长,再利用三角形的面积公式进行计算,可求出△ABD的面积.
30.【答案】6
【解析】【解答】解:如图:
以BC为公共边可画出△BDC,△BEC,△BFC三个三角形和原三角形全等.
以AB为公共边可画出三个三角形△ABG,△ABM,△ABH和原三角形全等.
所以可画出6个.
故答案为:6.
【分析】根据网格的特点及全等三角形的性质可以以AB和BC为公共边分别画出3个,而AC得不到,从而得出结论.
31.【答案】4
【解析】【解答】解:如图所示,可供选择的地址有4个.
故答案为:4.
【分析】由三角形内角平分线的交点到三角形三边的距离相等,可得三角形内角平分线的交点满足条件;然后利用角平分线的性质,可证得三角形两条外角平分线的交点到其三边的距离也相等,这样的点有3个,可得可供选择的地址有4个.
32.【答案】解:连接 ,作 的垂直平分线,再作 的平分线,
垂直平分线与角平分线的交点即为
P为油库所在地,如图所示.
【解析】【分析】连接 AB ,作 AB 的垂直平分线,再作 的平分线,垂直平分线与角平分线的交点即为油库的所在地.
33.【答案】(1)解:如图
(2)解:∵∠A=100°,∠C=28°,
∴,
又∵BD平分∠ABC,
∴∠DBC=26°,
∴.
【解析】【分析】(1)以点B为圆心,任意长为半径画弧,与AB、BC交于两点,然后分别以这两点为圆心,以大于两点间距离的一半为半径画弧,交于一点,连接该点与点B,并延长,与AC交于点D,则BD为∠ABC的平分线;
(2)根据内角和定理可得∠ABC=52°,根据角平分线的概念可得∠DBC=26°,由外角的性质可得∠BDA=∠DBC+∠C,据此计算.
34.【答案】C
【解析】【解答】如图,角A、B、C对应的中点分别是D、E、F,且三条中线交点是O,将OD延长到G,使OD=DG,连接BG,设BE=5,CF=10,AD则为第三条中线长
∵角A、B、C对应的中点分别是D、E、F,且三条中线交点是O
∴ ,
∵OD=DG
∴
∴
∴
∴
∵第三条中线的长也是整数
∴第三条中线长的最大值为14
故答案为:C.
【分析】如图,角A、B、C对应的中点分别是D、E、F,且三条中线交点是O,将OD延长到G,使OD=DG,连接BG,设BE=5,CF=10,AD则为第三条中线长,根据三角形的三边关系和中线的性质列出不等式组,即可求出第三条中线长的最大值.
35.【答案】A
【解析】【解答】A、∵=2=-(-2),∴|a|>-a,错误,符合题意;
B、=>-, 正确,不符合题意;
C、=1>-1, 正确,不符合题意;
D、=-,正确,不符合题意;
故答案为:A.
【分析】当a>0时,|a|>-a,当a≤0时,|a|=-a,据此逐项分析即可判断.
36.【答案】D
【解析】【解答】∵PB+PC=BC,
而PA+PC=BC,
∴PA=PB,
∴点P在AB的垂直平分线上,
即点P为AB的垂直平分线与BC的交点.
故选D.
【分析】由PB+PC=BC和PA+PC=BC易得PA=PB,根据线段垂直平分线定理的逆定理可得点P在AB的垂直平分线上,于是可判断D选项正确.
37.【答案】C
【解析】【解答】解: ① ∵EF∥BC,∴∠EGB=∠CBG,∵∠EBG=CBG,∴∠EBG=∠EGB,∴EB=EG,同理FC=FG,EF=EG+FG=BE+CF,正确;
②∵BG和CG分别是∠ABC和∠ACB的平分线,∴∠CBG=∠ABC,∠BCG=∠ACB,∠BGC=180°-∠CBG-∠BCG=180°-(∠ABC+∠ACB)=180°-(180°-∠A)=90°+ ∠A ,正确;
③如图,过G作GN⊥AB,GM⊥BC,
∵BG是∠ABC的平分线,∴GN=GM,∵CG是∠ACB的平分线,∴GM=GD,∴GM=GN=GD,即
点G到 △ABC 各边的距离相等,正确;
④如图,连接AG,
S△AEF=S△AEG+S△AFG=AE×GN+AF×GD=(AE+AF)×GD=mn,错误.
综上,正确的有3项.
故答案为:C.
【分析】利用角的平分线和过平分线的一点作角的一边的平行线可得等腰三角形,推出EF等于BE和CF之和;根据角平分线的性质,结合三角形内角和定理把∠BGC用∠ABC和∠ACB表示,从而可把∠BGC用含∠A的关系式表示;因为G是三角形两角平分线的交点,根据角平分线性质定理可得点G到三角形的三边距离相等;用分割法求三角形面积,可得△AEF的面积是mn.
38.【答案】40°
【解析】【解答】∵∠A=20°,∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=160°,
∵BD1平分∠ABC,CD1平分∠ACB,
∴∠ABD1= ∠ABC,∠ACD1= ∠ACD,
∵BD2平分∠ABD1,CD2平分∠ACD1,
∴∠ABD2= ∠ABD1= ∠ABC,∠ACD2= ∠ACD1= ∠ACB,
同理可得∠ABD= ∠ABC,∠ACD= ∠ACB,
∴∠ABD+∠ACD=160°× =20°,
∴∠BCD+∠CBD=140°
∴∠BDC=180﹣∠BCD﹣∠CBD=40°
故答案为40°.
【分析】根据题意可得∠ABC+∠ACB=160°,BD1,CD1,CD2,BD2…BDn,CDn是角平分线,可得∠ABDn+∠ACDn=160×( )n,可求∠BCDn+∠CBDn的值,再根据三角形内角和定理可求结果.
39.【答案】11
【解析】【解答】解:如图:作PE⊥OB,PG⊥OA,PF⊥MN,连结OP,
∵PM、PN分别平分∠AMN,∠BNM,
∴PF=PG=PE,
∵S△PMN=·MN·PF=2,MN=2,
∴PF=PG=PE=2,
由题易得:
△GMP≌△GFP,△FPN≌△EPN,△OPG≌△OEP,
∴GM=GF,FN=NE,OG=OE,
∴S△OPG=S△OPE=×(2+2+7)=,
即S△OPG=·OG·PG=,
∴OG=,
∴C△MON=OM+ON+MN,
=OM+ON+MF+FN,
=OM+ON+MG+NE,
=OG+OE,
=2OG,
=2×,
=11.
故答案为:11.
【分析】作PE⊥OB,PG⊥OA,PF⊥MN,连结OP,根据角平分线的性质定理得PF=PG=PE,再由三角形面积公式得PF=PG=PE=2,据条件易得:△GMP≌△GFP,△FPN≌△EPN,△OPG≌△OEP,由全等三角形性质得GM=GF,FN=NE,OG=OE,S△OPG=·OG·PG=得OG=,由三角形周长和等量代换可得答案.
40.【答案】(1);BD
(2);边AB的中线
【解析】【解答】(1)如图所示,BD为所求作的垂线,点B到直线AC的距离是线段BD的长度,
故答案为:BD;(2)如图所示,EF为所求作的线段AB的垂直平分线,
线段CM是△ABC的边AB的中线,
故答案为:边AB的中线.
【分析】(1)以点B为圆心,以任意长为半径画弧,与AC的延长线相交于两点,在以这两点为圆心,以大于它们距离的一半为半径画弧,两弧相交于一点,连接点B与这一点与AC的延长线相交于点D,则点D即为所求,根据点到直线的距离解答;(2)分别以点A、B为圆心,以大于 AB为半径画弧,两弧相交于两点,过这两点作直线EF即可,根据线段垂直平分线的定义可得点M是AB的中点,然后根据中线的定义解答.
41.【答案】(1)证明:、分别平分和,
,
,
,
;
(2)证明:,
,
,
如图,过点作,交于点,
,
,
,,
在和中,,
,
,
,
.
【解析】【分析】(1)利用角平分线和三角形的内角和计算求解即可;
(2)先求出AE=EB,再利用全等三角形的判定与性质求解即可。
42.【答案】(1)解:根据题意,如图:
(2)解:EF=EG;
理由如下:如图,
∵点M为线段OD的中点,EM⊥OD,
∴线段EM是△OED的高,也是中线,
∴EM垂直平分OD,∠OME=90°,
∴OE=DE,
∴∠EDO=∠AOB=∠OEF=45°,
∵OC是∠AOB的角平分线,
∴∠AOC=∠BOC,
∴∠AOC+∠OEF=∠BOC+∠EDO,
∴∠EFG=∠EGF,
∴EF=EG;
(3)解:在射线EA上,截取EH=EG,连接GH,如图:
则EH=EF,
∵OE=DE,
∴ED+EF=OE+EH=OH,
∵∠EDO=∠EOM=∠OEF=45°,点M是OD的中点,
∴OM=EM=DM,∠DEA=45°+45°=90°,
∴OD=2EM;∠EHG=45°,
∵∠AOC=∠BOC,OG=OG,
∴△ODG≌△OHG(AAS),
∴OD=OH,
∴ED+EF=2EM.
【解析】【分析】(1)根据要求画出图形即可;
(2)结论:EF=EG,欲证明EF=EG,只要证明∠EFG=∠EGF=67.5°即可;
(3)过点G作OD的垂线,垂足为N,证明GN=EG=EF,ON=OE=ED,可得结论。
43.【答案】(1)解: 与 全等,
理由如下:当 时, ,
则 ,
∴ ,
又∵ ,
在 和 中,
∴ ;
(2)解: ,
证明:∵ ,
∴ ,
∴ .
∴ ,
即 ;
(3)解: , ,
①若
则 , ,
∴ ,
解得: ,则 ;
②若 ,
则 , ,
则 ,解得, ,
∴ ,解得, ,
故当 , 或 , 时, 与 全等.
【解析】【分析】(1)当t=1时求得 ,再利用SAS即可证明 ;(2)根据 ,推出 ,即可证明 ;(3)分 及 两种情况判断即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
