2022-2023学年浙教版数学九年级上册3.1 圆 同步精练 (含答案)
文档属性
| 名称 | 2022-2023学年浙教版数学九年级上册3.1 圆 同步精练 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 521.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 08:14:46 | ||
图片预览


文档简介
3.1 圆 同步精练
一、单选题
1.如图,已知A,B,C,D四点都在⊙O上,则⊙O中的弦的条数为( )
A.2 B.3 C.4 D.5
2.半径为5的圆的一条弦长不可能是( )
A.3 B.5 C.10 D.12
3.如图①,若BC是Rt△ABC和Rt△DBC的公共斜边,则A、B、C、D在以BC为直径的圆上,则叫它们“四点共圆”.如图②,△ABC的三条高AD、BE、CF相交于点H,则图②中“四点共圆”的组数为( )
A.2 B.3 C.4 D.6
4.已知点是数轴上一定点,点是数轴上一动点,点表示的实数为,点所表示的实数为,作以为圆心,为半径的,若点在外,则的值可能是().
A. B. C. D.
5.下列说法:①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,但弧不一定是半圆.正确的说法有( )
A.1个 B.2个 C.3个 D.4个
6.已知⊙O的半径是5,点A到圆心O的距离是7,则点A与⊙O的位置关系是( )
A.点A在⊙O B.点A在⊙O内 C.点A在⊙O外 D.点A与圆心O重合
7.如果一个圆的半径由1厘米增加到2厘米.那么这个圆的周长增加了( )
A.3.14厘米 B.2厘米 C.8厘米 D.4厘米
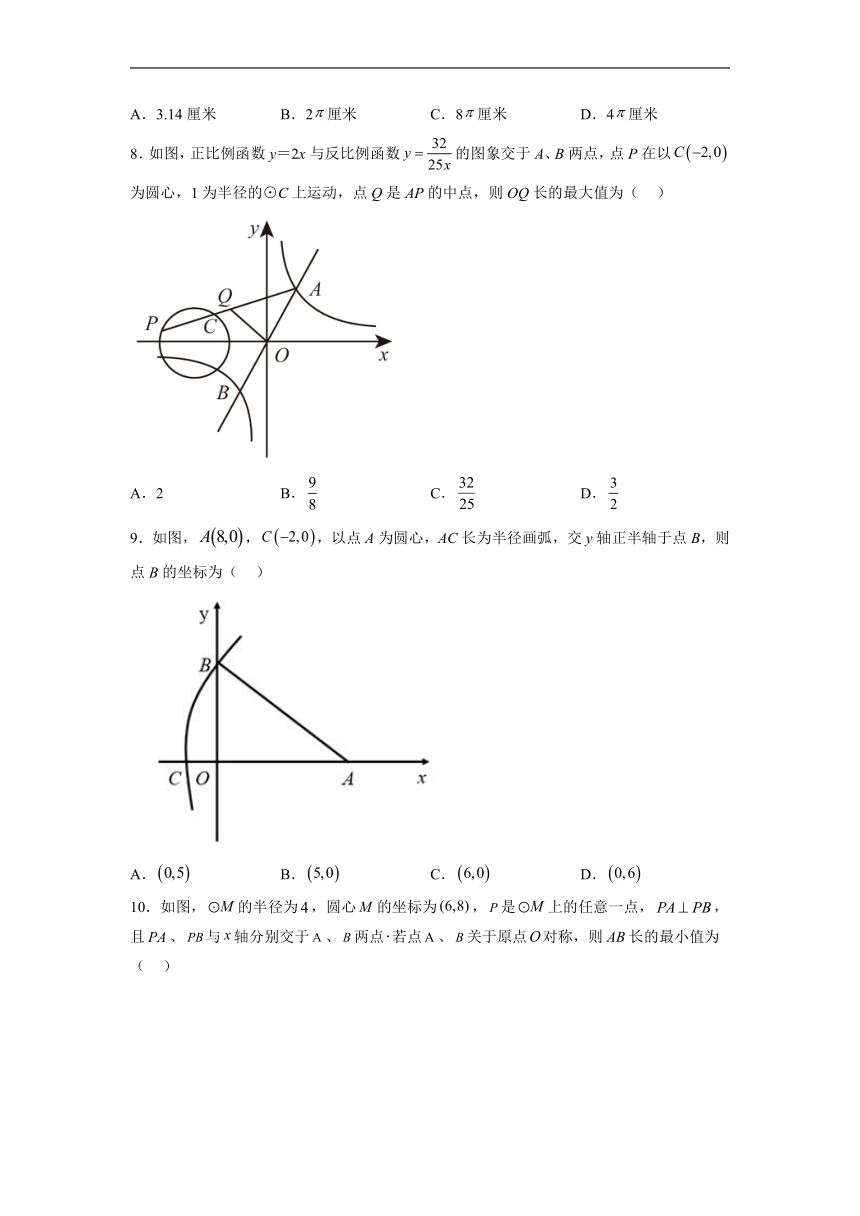
8.如图,正比例函数y=2x与反比例函数的图象交于A、B两点,点P在以为圆心,1为半径的⊙C上运动,点Q是AP的中点,则OQ长的最大值为( )
A.2 B. C. D.
9.如图,,,以点A为圆心,AC长为半径画弧,交y轴正半轴于点B,则点B的坐标为( )
A. B. C. D.
10.如图,的半径为,圆心的坐标为,是上的任意一点,,且、与轴分别交于、两点若点、关于原点对称,则长的最小值为( )
A. B. C. D.
11.已知⊙O的直径为3cm,点P到圆心O的距离OP=2cm,则点P( )
A.在⊙O外 B.在⊙O上 C.在⊙O内 D.不能确定
12.如图,中,,,,以点为圆心3为半径的优弧分布交,于点,点优弧上的动点,点为的中点,则长的取值范围是( )
A. B. C.D.
二、填空题
13.到定点的距离等于定长的所有点组成的图形是____________.
14.如图,一枚圆形古钱币的中间是一个正方形孔,已知圆的直径与正方形的对角线之比为3∶1,则圆的面积约为正方形面积的________倍.(精确到个位)
15.若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=8,则S△ABC=___________.
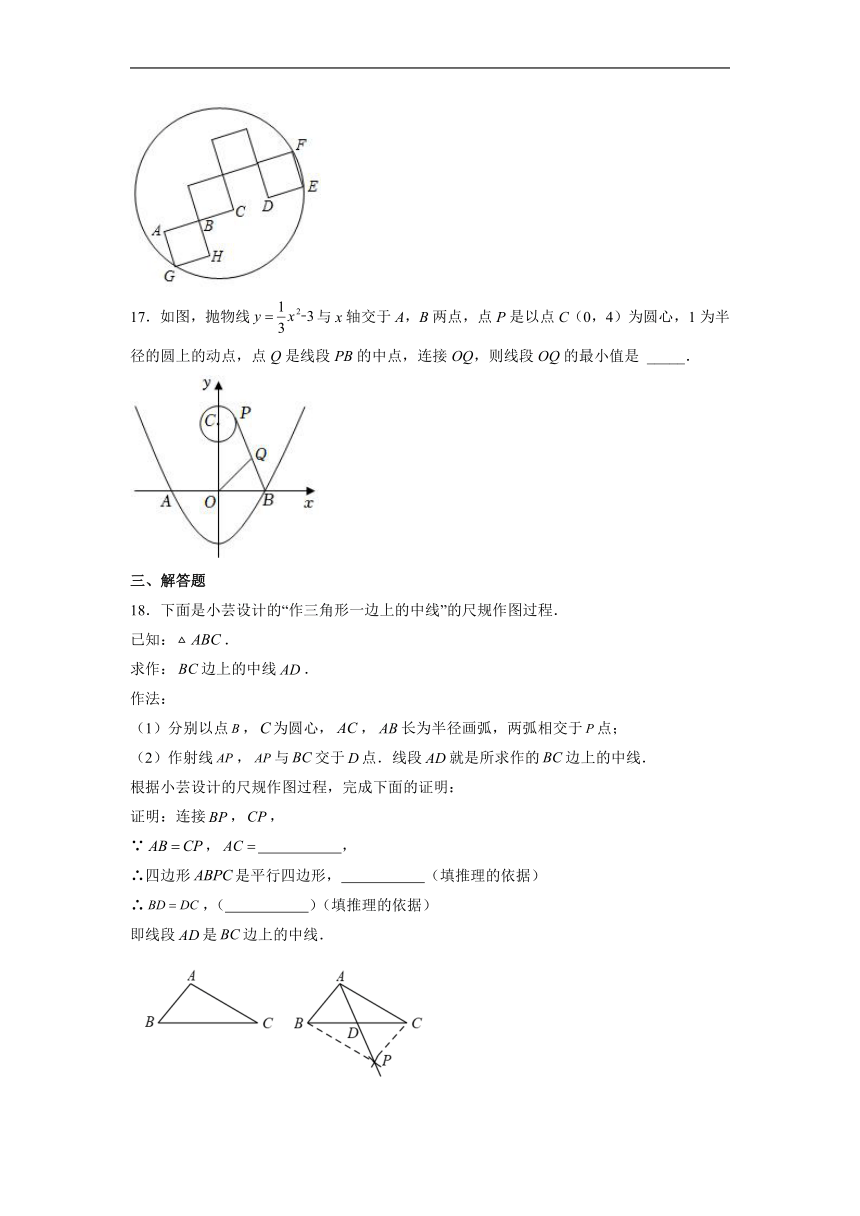
16.如图,圆内4个正方形的边长均为2a,若点A,B,C,D,E在同一条直线上,点E,F,G在同一个圆上,则此圆的半径为______.
17.如图,抛物线与x轴交于A,B两点,点P是以点C(0,4)为圆心,1为半径的圆上的动点,点Q是线段PB的中点,连接OQ,则线段OQ的最小值是 _____.
三、解答题
18.下面是小芸设计的“作三角形一边上的中线”的尺规作图过程.
已知:.
求作:边上的中线.
作法:
(1)分别以点,为圆心,,长为半径画弧,两弧相交于点;
(2)作射线,与交于点.线段就是所求作的边上的中线.
根据小芸设计的尺规作图过程,完成下面的证明:
证明:连接,,
∵, ,
∴四边形是平行四边形, (填推理的依据)
∴,( )(填推理的依据)
即线段是边上的中线.
19.如图,已知△ABC为等腰三角形,AD⊥BC;
(1)尺规作图:作△ABC的外接圆⊙O(保留作图痕迹,不写作法);
(2)若底边,腰,求△ABC外接圆⊙O的半径.
20.如图所示,为的一条弦,点为上一动点,且,点,分别是,的中点,直线与交于,两点,若的半径为7,求的最大值.
21.对于平面内⊙C和⊙C外一点P,若过点P的直线l与⊙C有两个不同的公共点M,N,点Q为直线l上的另一点,且满足(如图1所示),则称点Q是点P关于⊙O的密切点.已知在平面直角坐标系xOy中,⊙C的半径为2,点P(4,0).
(1)在点D(﹣2,1),E(1,0),F(3,)中,是点P关于⊙O的密切点的为 .
(2)设直线l方程为y=kx+b,如图2所示,
①k=时,求出点P关于O的密切点Q的坐标;
②⊙T的圆心为T(t,0),半径为2,若⊙T上存在点P关于⊙O的密切点,直接写出t的取值范围.
参考答案
1--10BDDAC CBDDC 11--12AA
13.圆
14.14
15.32+16或32﹣16
16.a
17.2
18.证明:连接,,
∵,BP,
∴四边形是平行四边形,(两组对边分别相等的四边形是平行四边形)
∴,(平行四边形的对角线互相平分)
即线段是边上的中线.
19.(1)解:如图所示:
如图是所求作的的外接圆.
(2)
解:如图: ∵是等腰三角形,底边,腰,
∴,
∴在中,.
在中,.
∴.
20.连结,,
∵ ∴
∴为等边三角形,
∵点,分别是,的中点
∴,∵ 为的一条弦
∴最大值为直径14 ∴的最大值为.
21.(1)当圆心在坐标原点时,直线l为y=0时,
∵⊙O的半径为2,点P(4,0),
∴M(2,0),N(﹣2,0),PM=2,PN=6,=,
∵,
∴,
设Q点坐标为(x,y),则QM=|2﹣x|,QN=|x﹣(﹣2)|=|x+2|,
∴,
∴|2+x|=3|2﹣x|,
∴2+x=6﹣3x,或2+x=3x﹣6,
∴x=1或x=4,
∴E(1,0)是点P关于⊙O的密切点.
故答案为:E.
(2)①依题意直线l:y=kx+b过定点P(4,0),
∵k=,
∴将P(4,0)代入y=x+b得:0=×4+b,
∴b=,
∴y=x+.
如图,作MA⊥x轴于点A,NB垂直x轴于点B,
设M(x, x+),由OM=2得:,
∴5x2﹣4x﹣10=0,
则M,N两点的横坐标,是方程5x2﹣4x﹣10=0的两根,
解得,,
∴AB=,PA=,PB=,
∵,
∴,
∴,
∴HA=,
∴OH=OA﹣HA=,
∴Q(1,1).
②点P关于⊙O的密切点的轨迹为切点弦ST(不含端点),如图所示:
∴﹣1≤t<0或2<t≤3.
一、单选题
1.如图,已知A,B,C,D四点都在⊙O上,则⊙O中的弦的条数为( )
A.2 B.3 C.4 D.5
2.半径为5的圆的一条弦长不可能是( )
A.3 B.5 C.10 D.12
3.如图①,若BC是Rt△ABC和Rt△DBC的公共斜边,则A、B、C、D在以BC为直径的圆上,则叫它们“四点共圆”.如图②,△ABC的三条高AD、BE、CF相交于点H,则图②中“四点共圆”的组数为( )
A.2 B.3 C.4 D.6
4.已知点是数轴上一定点,点是数轴上一动点,点表示的实数为,点所表示的实数为,作以为圆心,为半径的,若点在外,则的值可能是().
A. B. C. D.
5.下列说法:①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,但弧不一定是半圆.正确的说法有( )
A.1个 B.2个 C.3个 D.4个
6.已知⊙O的半径是5,点A到圆心O的距离是7,则点A与⊙O的位置关系是( )
A.点A在⊙O B.点A在⊙O内 C.点A在⊙O外 D.点A与圆心O重合
7.如果一个圆的半径由1厘米增加到2厘米.那么这个圆的周长增加了( )
A.3.14厘米 B.2厘米 C.8厘米 D.4厘米
8.如图,正比例函数y=2x与反比例函数的图象交于A、B两点,点P在以为圆心,1为半径的⊙C上运动,点Q是AP的中点,则OQ长的最大值为( )
A.2 B. C. D.
9.如图,,,以点A为圆心,AC长为半径画弧,交y轴正半轴于点B,则点B的坐标为( )
A. B. C. D.
10.如图,的半径为,圆心的坐标为,是上的任意一点,,且、与轴分别交于、两点若点、关于原点对称,则长的最小值为( )
A. B. C. D.
11.已知⊙O的直径为3cm,点P到圆心O的距离OP=2cm,则点P( )
A.在⊙O外 B.在⊙O上 C.在⊙O内 D.不能确定
12.如图,中,,,,以点为圆心3为半径的优弧分布交,于点,点优弧上的动点,点为的中点,则长的取值范围是( )
A. B. C.D.
二、填空题
13.到定点的距离等于定长的所有点组成的图形是____________.
14.如图,一枚圆形古钱币的中间是一个正方形孔,已知圆的直径与正方形的对角线之比为3∶1,则圆的面积约为正方形面积的________倍.(精确到个位)
15.若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=8,则S△ABC=___________.
16.如图,圆内4个正方形的边长均为2a,若点A,B,C,D,E在同一条直线上,点E,F,G在同一个圆上,则此圆的半径为______.
17.如图,抛物线与x轴交于A,B两点,点P是以点C(0,4)为圆心,1为半径的圆上的动点,点Q是线段PB的中点,连接OQ,则线段OQ的最小值是 _____.
三、解答题
18.下面是小芸设计的“作三角形一边上的中线”的尺规作图过程.
已知:.
求作:边上的中线.
作法:
(1)分别以点,为圆心,,长为半径画弧,两弧相交于点;
(2)作射线,与交于点.线段就是所求作的边上的中线.
根据小芸设计的尺规作图过程,完成下面的证明:
证明:连接,,
∵, ,
∴四边形是平行四边形, (填推理的依据)
∴,( )(填推理的依据)
即线段是边上的中线.
19.如图,已知△ABC为等腰三角形,AD⊥BC;
(1)尺规作图:作△ABC的外接圆⊙O(保留作图痕迹,不写作法);
(2)若底边,腰,求△ABC外接圆⊙O的半径.
20.如图所示,为的一条弦,点为上一动点,且,点,分别是,的中点,直线与交于,两点,若的半径为7,求的最大值.
21.对于平面内⊙C和⊙C外一点P,若过点P的直线l与⊙C有两个不同的公共点M,N,点Q为直线l上的另一点,且满足(如图1所示),则称点Q是点P关于⊙O的密切点.已知在平面直角坐标系xOy中,⊙C的半径为2,点P(4,0).
(1)在点D(﹣2,1),E(1,0),F(3,)中,是点P关于⊙O的密切点的为 .
(2)设直线l方程为y=kx+b,如图2所示,
①k=时,求出点P关于O的密切点Q的坐标;
②⊙T的圆心为T(t,0),半径为2,若⊙T上存在点P关于⊙O的密切点,直接写出t的取值范围.
参考答案
1--10BDDAC CBDDC 11--12AA
13.圆
14.14
15.32+16或32﹣16
16.a
17.2
18.证明:连接,,
∵,BP,
∴四边形是平行四边形,(两组对边分别相等的四边形是平行四边形)
∴,(平行四边形的对角线互相平分)
即线段是边上的中线.
19.(1)解:如图所示:
如图是所求作的的外接圆.
(2)
解:如图: ∵是等腰三角形,底边,腰,
∴,
∴在中,.
在中,.
∴.
20.连结,,
∵ ∴
∴为等边三角形,
∵点,分别是,的中点
∴,∵ 为的一条弦
∴最大值为直径14 ∴的最大值为.
21.(1)当圆心在坐标原点时,直线l为y=0时,
∵⊙O的半径为2,点P(4,0),
∴M(2,0),N(﹣2,0),PM=2,PN=6,=,
∵,
∴,
设Q点坐标为(x,y),则QM=|2﹣x|,QN=|x﹣(﹣2)|=|x+2|,
∴,
∴|2+x|=3|2﹣x|,
∴2+x=6﹣3x,或2+x=3x﹣6,
∴x=1或x=4,
∴E(1,0)是点P关于⊙O的密切点.
故答案为:E.
(2)①依题意直线l:y=kx+b过定点P(4,0),
∵k=,
∴将P(4,0)代入y=x+b得:0=×4+b,
∴b=,
∴y=x+.
如图,作MA⊥x轴于点A,NB垂直x轴于点B,
设M(x, x+),由OM=2得:,
∴5x2﹣4x﹣10=0,
则M,N两点的横坐标,是方程5x2﹣4x﹣10=0的两根,
解得,,
∴AB=,PA=,PB=,
∵,
∴,
∴,
∴HA=,
∴OH=OA﹣HA=,
∴Q(1,1).
②点P关于⊙O的密切点的轨迹为切点弦ST(不含端点),如图所示:
∴﹣1≤t<0或2<t≤3.
同课章节目录
