2022-2023学年浙教版九年级数学上册《3.3垂径定理》同步自主提升训练(含答案)
文档属性
| 名称 | 2022-2023学年浙教版九年级数学上册《3.3垂径定理》同步自主提升训练(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 374.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-28 08:22:29 | ||
图片预览



文档简介
2022-2023学年浙教版九年级数学上册《3.3垂径定理》同步自主提升训练题(附答案)
一.选择题
1.把半径长为2.5的球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知CD=4,则EF=( )
A.2 B.2.5 C.4 D.5
2.如图,AB是⊙O的直径,弦CD⊥AB于点E,AC=CD,⊙O的半径为2,则△AOC的面积为( )
A. B.2 C.2 D.4
3.如图,⊙O的直径AB与弦CD相交于点P,且∠APC=45°,若PC2+PD2=8,则⊙O的半径为( )
A. B.2 C.2 D.4
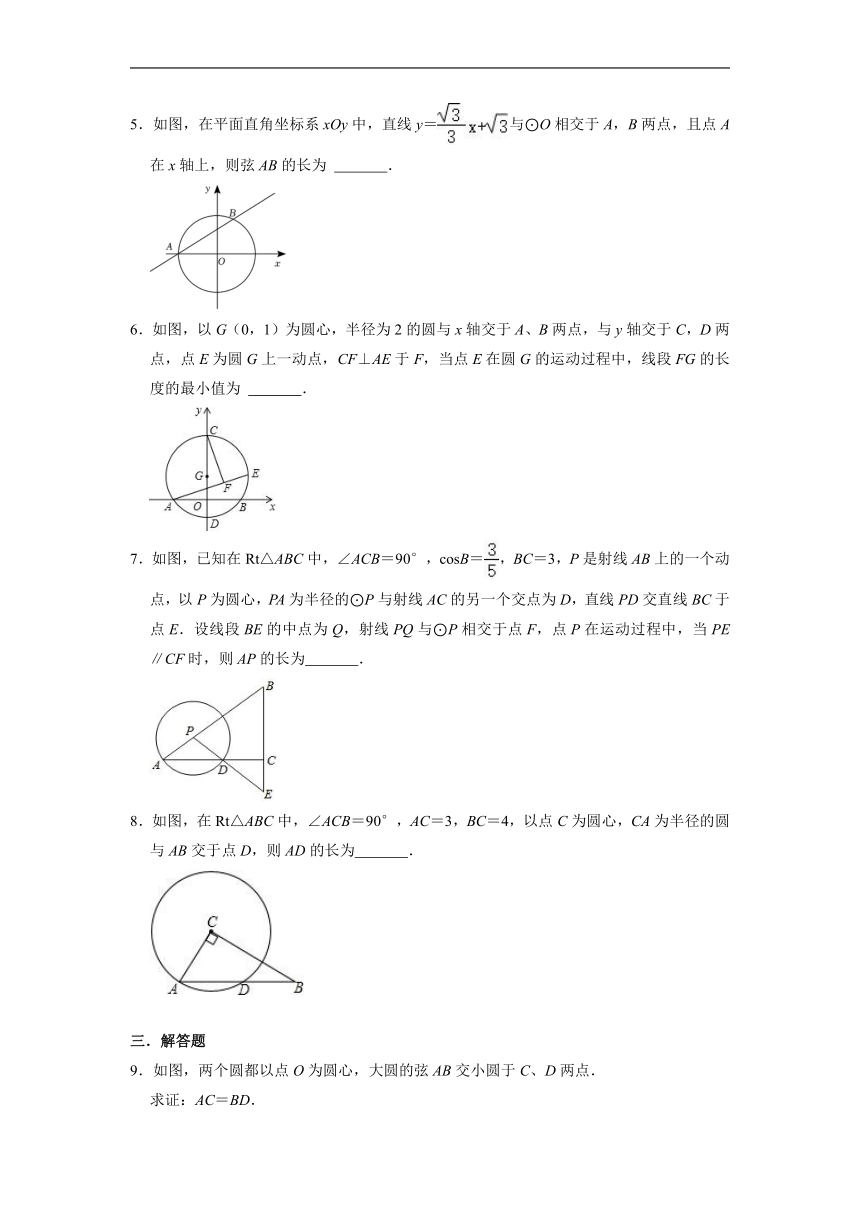
4.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8,OF=,则OE的长为( )
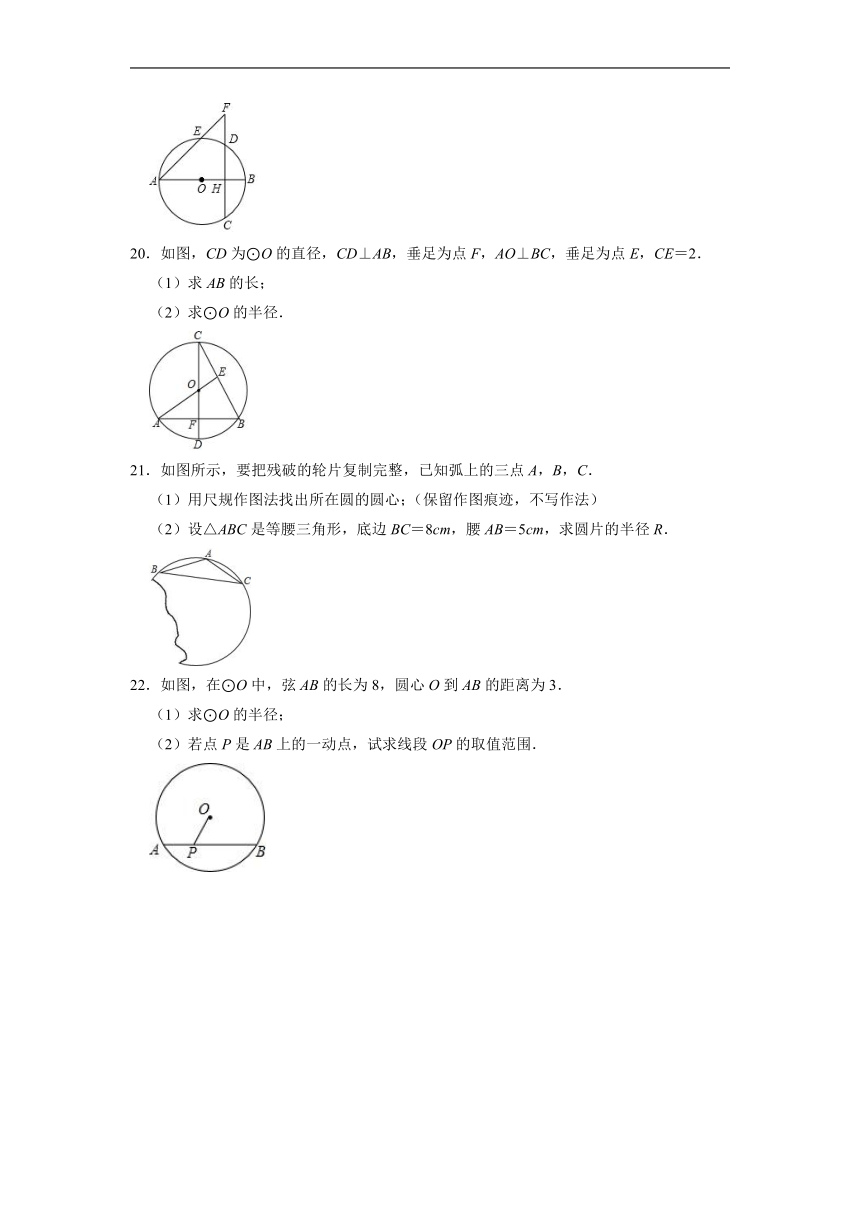
A.3 B.4 C.2 D.5
二.填空题
5.如图,在平面直角坐标系xOy中,直线y=与⊙O相交于A,B两点,且点A在x轴上,则弦AB的长为 .
6.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为圆G上一动点,CF⊥AE于F,当点E在圆G的运动过程中,线段FG的长度的最小值为 .
7.如图,已知在Rt△ABC中,∠ACB=90°,cosB=,BC=3,P是射线AB上的一个动点,以P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.设线段BE的中点为Q,射线PQ与⊙P相交于点F,点P在运动过程中,当PE∥CF时,则AP的长为 .
8.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为 .
三.解答题
9.如图,两个圆都以点O为圆心,大圆的弦AB交小圆于C、D两点.
求证:AC=BD.
10.如图,已知AB是圆O的直径,弦CD交AB于点E,∠CEA=30°,OE=4,DE=5,求弦CD及圆O的半径长.
11.如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm.若水面上升2cm(EG=2cm),则此时水面宽AB为多少?
12.如图所示,一座圆弧形拱桥的跨度AB长为40米,桥离水面最大距离CD为10米,若有一条水面上宽度为30米,高度为6米的船能否通过这座桥?请说明理由.
13.如图,⊙O的半径OB=5cm,AB是⊙O的弦,点C是AB延长线上一点,且∠OCA=30°,OC=8cm,求AB的长.
14.一根横截面为圆形的下水管道的直径为1米,管内有少量的污水(如图),此时的水面宽AB为0.6米.
(1)求此时的水深(即阴影部分的弓形高);
(2)当水位上升到水面宽为0.8米时,求水面上升的高度.
15.如图,D是⊙O弦BC的中点,A是⊙O上的一点,OA与BC交于点E,已知AO=8,BC=12.
(1)求线段OD的长;
(2)当EO=BE时,求DE的长.
16.⊙O中,直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,且∠DEB=60°,求CD的长.
17.已知:圆O的半径长为5,弦AB与弦CD平行,AB=6,CD=8.求弦AB与弦CD之间的距离.
18.如图,OA=OB,AB交⊙O于点C、D,AC与BD是否相等?为什么?
19.如图,已知AB是圆O的直径,弦CD⊥AB,垂足H在半径OB上,AH=5,CD=,点E在弧AD上,射线AE与CD的延长线交于点F.
(1)求圆O的半径;
(2)如果AE=6,求EF的长.
20.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,CE=2.
(1)求AB的长;
(2)求⊙O的半径.
21.如图所示,要把残破的轮片复制完整,已知弧上的三点A,B,C.
(1)用尺规作图法找出所在圆的圆心;(保留作图痕迹,不写作法)
(2)设△ABC是等腰三角形,底边BC=8cm,腰AB=5cm,求圆片的半径R.
22.如图,在⊙O中,弦AB的长为8,圆心O到AB的距离为3.
(1)求⊙O的半径;
(2)若点P是AB上的一动点,试求线段OP的取值范围.
参考答案
一.选择题
1.解:设球的平面投影圆心为O,过点O作ON⊥AD于点N,延长NO交BC于点M,连接OF,如图所示:
则NF=EN=EF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDNM是矩形,
∴MN=CD=4,ON=MN﹣OM=4﹣2.5=1.5,
在Rt△ONF中,由勾股定理得:ON2+NF2=OF2,
∴NF==2,EF=2NF=4,
故选:C.
2.解:∵CD⊥AB,
∴CE=DE=,∠AEC=90°,
∵AC=CD,
∴CE=,
∴∠A=30°,
∵OA=OC,
∴∠A=∠OCA=30°,
∴∠COE=60°,
∴CE=,
∴S△AOC=
=
=.故选:C.
3.解:作CM⊥AB于M,DN⊥AB于N,连接OC,OD,
∴∠NDP=∠MCP=∠APC=45°
又∵OC=OD,
∴∠ODP=∠OCP,
∵∠COM=45°+∠OCD,∠ODN=45°+∠ODC,
∴∠NDO=∠COM,
在Rt△ODN与Rt△COM中,
,
∴Rt△ODN≌Rt△COM,
∴ON=CM=PM,OM=ND=PN
又∵OC2=CM2+OM2,OD2=DN2+ON2
∴OC2=CM2+PN2,OD2=DN2+PM2
∴OC2+OD2=CM2+PN2+DN2+PM2=PC2+PD2=8
∴OC2=4,
∴OC=2,
故选:B.
4.解:连接OB、AB,
∵BD⊥AO,BD=8,
∴BE=ED=BD=4,
∵OF⊥BC,
∴CF=FB,
∵CO=OA,OF=,
∴AB=2OF=2,
由勾股定理得:AE==2,
在Rt△BOE中,OB2=OE2+BE2,
即OA2=(OA﹣2)2+42,
解得:OA=5,
∴OE=OA﹣AE=5﹣2=3.
故选:A.
二.填空题
5.解:过O作OM⊥直线AB与M,直线AB交y轴于C,
y=,
当x=0时,y=,
当y=0时,x+=0,解得:x=﹣3,
所以OC=,OA=3,
∴∠CAO=30°,
∵OM⊥AC,
∴∠OMA=90°,
∴OM=OA=,
由勾股定理得:AM===,
∵OM⊥AB,OM过圆心O,
∴AM=BM=,
∴AB=AM+BM=+=3,
故答案为:3.
6.解:作GM⊥AC于M,连接AG.
∵GO⊥AB,
∴OA=OB,
在Rt△AGO中,AG=2,OG=1,
∴AG=2OG,OA===,
∴∠GAO=30°,AB=2AO=2,
∴∠AGO=60°,
∵GC=GA,
∴∠GCA=∠GAC,
∵∠AGO=∠GCA+∠GAC,
∴∠GCA=∠GAC=30°,
∴AC=2OA=2,MG=CG=1,
∵∠AFC=90°,
∴点F在以AC为直径的⊙M上,
当点F在MG的延长线上时,FG的长最小,最小值=FM﹣GM=﹣1.
故答案为:﹣1.
7.解:如图,连接CF,过点P作PG⊥AC于G,设PA=x.
在Rt∠ACB中,∵ACB=90°,BC=3,=,
∴AB=5,AC===4,
∵PG⊥AD,
∴AG=DG=x,
∴AD=x,CD=4﹣x,
∵∠ABC+∠A=90°,∠PEC+∠CDE=90°,
∵∠A=∠PDA,
∴∠ABC=∠PEC,
∵∠ABC=∠EBP,
∴∠PEC=∠EBP,
∴PB=PE,
∵点Q为线段BE的中点,
∴PQ⊥BC,
∴PQ∥AC
∴当PE∥CF时,四边形PDCF是平行四边形,
∴PF=CD,
当点P在边AB的上时,x=4﹣x,x=,
当点P在边AB的延长线上时,x=x﹣4,x=,
综上所述,当PE∥CF时,AP的长为或.
8.解:过点C作CE⊥AD于点E,
则AE=DE,
∵∠ACB=90°,AC=3,BC=4,
∴AB==5,
∵S△ABC=AC BC=AB CE,
∴CE==,
∴AE==,
∴AD=2AE=,
故答案为.
三.解答题
9.证明:过点O作OE⊥AB,
∵OA=OB,
∴AE=BE,
又∵在⊙O中,
∴CE=DE,
∴AC=BD
10.解:过点O作OM⊥CD于点M,联结OD,
∵∠CEA=30°,∴∠OEM=∠CEA=30°,
在Rt△OEM中,∵OE=4,
∴,,
∵,
∴,
∵OM过圆心,OM⊥CD,
∴CD=2DM,
∴,
∵,
∴在Rt△DOM中,,
∴弦CD的长为,⊙O的半径长为.
11.解:连接OA、OC,
∵由题意知:AB∥CD,OE⊥AB,OF⊥CD,CD=20cm,
∴CG=CD=10cm,
在Rt△OGC中,由勾股定理得:OC2=CG2+OG2,
OC2=102+(OC﹣2)2,
解得:OC=26(cm),
则OE=26cm﹣2cm﹣2cm=22cm,
∵在Rt△OEA中,由勾股定理得:OA2=OE2+AE2,
∴262=222+AE2,
∴AE=8,
∵OE⊥AB,OE过圆心O,
∴AB=2AE=16cm.
12.解:如图,假设船能通过,弧形桥所在的圆恢复如图,
在Rt△AOD中,r2=202+(r﹣10)2,
解得r=25,
∴OD=r﹣10=15,
在Rt△OEG中,r2=152+OG2,
解得OG=20,
∴可以通过的船的高度为GD=OG﹣OD=20﹣15=5,
∵6>5,
∴船不能通过.
13.解:过点O作OD⊥AB于点D,连接OA,
∵在Rt△ODC中,∠OCA=30°,OC=8cm,
∴OD=OC=4cm,
∵在Rt△OAD中,OA=5cm,
∴AD==3,
∴AB=2AD=6.
14.解:(1)作半径OD⊥AB于C,连接OB,
由垂径定理得:BC=AB=0.3,
在Rt△OBC中,OC==0.4
CD=0.5﹣0.4=0.1,
此时的水深为0.1米;
(2)当水位上升到圆心以下时 水面宽0.8 米
则OC==0.3,
水面上升的高度为:0.3﹣0.2=0.1米;
当水位上升到圆心以上时,水面上升的高度为:0.4+0.3=0.7米,
综上可得,水面上升的高度为 0.1米或 0.7米.
15.解:(1)连接OB.
∵OD过圆心,且D是弦BC中点,
∴OD⊥BC,BD=BC,
在Rt△BOD中,OD2+BD2=BO2.
∵BO=AO=8,BD=6.
∴OD=2;
(2)在Rt△EOD中,OD2+ED2=EO2.
设BE=x,则OE=x,DE=6﹣x.
(2)2+(6﹣x)2=(x)2,
解得x1=﹣16(舍),x2=4.
则DE=2.
16.解:作OP⊥CD于P,连接OD,
∴CP=PD,
∵AE=1,EB=5,
∴AB=6,
∴OE=2,
在Rt△OPE中,OP=OE sin∠DEB=,
∴PD==,
∴CD=2PD=2(cm).
17.解:分两种情况:
(i)当两条弦在圆心O异侧时,如图1所示:
过O作OE⊥AB,交CD于F点,
连接OB,OD,可得出OB=OD=5,
∵AB∥CD,∴EF⊥CD,
∴E为AB中点,F为CD中点,
又∵AB=6,CD=8,
∴EB=3,FD=4,
在Rt△OEB和Rt△ODF中,
利用勾股定理得:OE==4,OF==3,
则弦AB与CD间的距离EF=OE+OF=4+3=7;
(ii)当两条弦在圆心O同侧时,如图2所示:
同理求出OE=4,OF=3,
则弦AB与CD间的距离EF=OE﹣OF=4﹣3=1.
综上,弦AB与CD间的距离为1或7.
18.解:AC与BD是相等,理由如下;
过点O作OE⊥AB,
∵OA=OB,
∴AE=BE,
又∵在⊙O中,
∴CE=DE,
∴AC=BD.
19.解:(1)连接OD,
∵直径AB⊥弦CD,CD=4,
∴DH=CH=CD=2,
在Rt△ODH中,AH=5,
设圆O的半径为r,
根据勾股定理得:OD2=(AH﹣OA)2+DH2,即r2=(5﹣r)2+20,
解得:r=4.5,
则圆的半径为4.5;
(2)过O作OG⊥AE于G,
∴AG=AE=×6=3,
∵∠A=∠A,∠AGO=∠AHF,
∴AF=,
∴EF=AF﹣AE=﹣6=.
20.解:(1)∵CD⊥AB,AO⊥BC
∴∠AFO=∠CEO=90°,
在△AOF和△COE中,
,
∴△AOF≌△COE,
∴CE=AF,
∵CE=2,
∴AF=2,
∵CD是⊙O的直径,CD⊥AB,
∴,
∴AB=4.
(2)∵AO是⊙O的半径,AO⊥BC
∴CE=BE=2,
∵AB=4,
∴,
∵∠AEB=90°,
∴∠A=30°,
又∵∠AFO=90°,
∴,即⊙O的半径是.
21.解:(1)作法:分别作AB和AC的垂直平分线,设交点为O,则O为所求圆的圆心;
(2)连接AO、BO,AO交BC于E,
∵AB=AC,
∴AE⊥BC,
∴BE=BC=×8=4,
在Rt△ABE中,AE===3,
设⊙O的半径为R,在Rt△BEO中,
OB2=BE2+OE2,
即R2=42+(R﹣3)2,
R=,
答:圆片的半径R为cm.
22.解:(1)作OC⊥AB于点C,
∵圆心O到AB的距离为3,
∴OC=3,
∵弦AB的长为8,
∴AC=BC=4,
∴OA==5,
∴⊙O的半径为5;
(2)∵点P是AB上的一动点,
∴3≤PO≤5.
一.选择题
1.把半径长为2.5的球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知CD=4,则EF=( )
A.2 B.2.5 C.4 D.5
2.如图,AB是⊙O的直径,弦CD⊥AB于点E,AC=CD,⊙O的半径为2,则△AOC的面积为( )
A. B.2 C.2 D.4
3.如图,⊙O的直径AB与弦CD相交于点P,且∠APC=45°,若PC2+PD2=8,则⊙O的半径为( )
A. B.2 C.2 D.4
4.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8,OF=,则OE的长为( )
A.3 B.4 C.2 D.5
二.填空题
5.如图,在平面直角坐标系xOy中,直线y=与⊙O相交于A,B两点,且点A在x轴上,则弦AB的长为 .
6.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为圆G上一动点,CF⊥AE于F,当点E在圆G的运动过程中,线段FG的长度的最小值为 .
7.如图,已知在Rt△ABC中,∠ACB=90°,cosB=,BC=3,P是射线AB上的一个动点,以P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.设线段BE的中点为Q,射线PQ与⊙P相交于点F,点P在运动过程中,当PE∥CF时,则AP的长为 .
8.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为 .
三.解答题
9.如图,两个圆都以点O为圆心,大圆的弦AB交小圆于C、D两点.
求证:AC=BD.
10.如图,已知AB是圆O的直径,弦CD交AB于点E,∠CEA=30°,OE=4,DE=5,求弦CD及圆O的半径长.
11.如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm.若水面上升2cm(EG=2cm),则此时水面宽AB为多少?
12.如图所示,一座圆弧形拱桥的跨度AB长为40米,桥离水面最大距离CD为10米,若有一条水面上宽度为30米,高度为6米的船能否通过这座桥?请说明理由.
13.如图,⊙O的半径OB=5cm,AB是⊙O的弦,点C是AB延长线上一点,且∠OCA=30°,OC=8cm,求AB的长.
14.一根横截面为圆形的下水管道的直径为1米,管内有少量的污水(如图),此时的水面宽AB为0.6米.
(1)求此时的水深(即阴影部分的弓形高);
(2)当水位上升到水面宽为0.8米时,求水面上升的高度.
15.如图,D是⊙O弦BC的中点,A是⊙O上的一点,OA与BC交于点E,已知AO=8,BC=12.
(1)求线段OD的长;
(2)当EO=BE时,求DE的长.
16.⊙O中,直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,且∠DEB=60°,求CD的长.
17.已知:圆O的半径长为5,弦AB与弦CD平行,AB=6,CD=8.求弦AB与弦CD之间的距离.
18.如图,OA=OB,AB交⊙O于点C、D,AC与BD是否相等?为什么?
19.如图,已知AB是圆O的直径,弦CD⊥AB,垂足H在半径OB上,AH=5,CD=,点E在弧AD上,射线AE与CD的延长线交于点F.
(1)求圆O的半径;
(2)如果AE=6,求EF的长.
20.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,CE=2.
(1)求AB的长;
(2)求⊙O的半径.
21.如图所示,要把残破的轮片复制完整,已知弧上的三点A,B,C.
(1)用尺规作图法找出所在圆的圆心;(保留作图痕迹,不写作法)
(2)设△ABC是等腰三角形,底边BC=8cm,腰AB=5cm,求圆片的半径R.
22.如图,在⊙O中,弦AB的长为8,圆心O到AB的距离为3.
(1)求⊙O的半径;
(2)若点P是AB上的一动点,试求线段OP的取值范围.
参考答案
一.选择题
1.解:设球的平面投影圆心为O,过点O作ON⊥AD于点N,延长NO交BC于点M,连接OF,如图所示:
则NF=EN=EF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDNM是矩形,
∴MN=CD=4,ON=MN﹣OM=4﹣2.5=1.5,
在Rt△ONF中,由勾股定理得:ON2+NF2=OF2,
∴NF==2,EF=2NF=4,
故选:C.
2.解:∵CD⊥AB,
∴CE=DE=,∠AEC=90°,
∵AC=CD,
∴CE=,
∴∠A=30°,
∵OA=OC,
∴∠A=∠OCA=30°,
∴∠COE=60°,
∴CE=,
∴S△AOC=
=
=.故选:C.
3.解:作CM⊥AB于M,DN⊥AB于N,连接OC,OD,
∴∠NDP=∠MCP=∠APC=45°
又∵OC=OD,
∴∠ODP=∠OCP,
∵∠COM=45°+∠OCD,∠ODN=45°+∠ODC,
∴∠NDO=∠COM,
在Rt△ODN与Rt△COM中,
,
∴Rt△ODN≌Rt△COM,
∴ON=CM=PM,OM=ND=PN
又∵OC2=CM2+OM2,OD2=DN2+ON2
∴OC2=CM2+PN2,OD2=DN2+PM2
∴OC2+OD2=CM2+PN2+DN2+PM2=PC2+PD2=8
∴OC2=4,
∴OC=2,
故选:B.
4.解:连接OB、AB,
∵BD⊥AO,BD=8,
∴BE=ED=BD=4,
∵OF⊥BC,
∴CF=FB,
∵CO=OA,OF=,
∴AB=2OF=2,
由勾股定理得:AE==2,
在Rt△BOE中,OB2=OE2+BE2,
即OA2=(OA﹣2)2+42,
解得:OA=5,
∴OE=OA﹣AE=5﹣2=3.
故选:A.
二.填空题
5.解:过O作OM⊥直线AB与M,直线AB交y轴于C,
y=,
当x=0时,y=,
当y=0时,x+=0,解得:x=﹣3,
所以OC=,OA=3,
∴∠CAO=30°,
∵OM⊥AC,
∴∠OMA=90°,
∴OM=OA=,
由勾股定理得:AM===,
∵OM⊥AB,OM过圆心O,
∴AM=BM=,
∴AB=AM+BM=+=3,
故答案为:3.
6.解:作GM⊥AC于M,连接AG.
∵GO⊥AB,
∴OA=OB,
在Rt△AGO中,AG=2,OG=1,
∴AG=2OG,OA===,
∴∠GAO=30°,AB=2AO=2,
∴∠AGO=60°,
∵GC=GA,
∴∠GCA=∠GAC,
∵∠AGO=∠GCA+∠GAC,
∴∠GCA=∠GAC=30°,
∴AC=2OA=2,MG=CG=1,
∵∠AFC=90°,
∴点F在以AC为直径的⊙M上,
当点F在MG的延长线上时,FG的长最小,最小值=FM﹣GM=﹣1.
故答案为:﹣1.
7.解:如图,连接CF,过点P作PG⊥AC于G,设PA=x.
在Rt∠ACB中,∵ACB=90°,BC=3,=,
∴AB=5,AC===4,
∵PG⊥AD,
∴AG=DG=x,
∴AD=x,CD=4﹣x,
∵∠ABC+∠A=90°,∠PEC+∠CDE=90°,
∵∠A=∠PDA,
∴∠ABC=∠PEC,
∵∠ABC=∠EBP,
∴∠PEC=∠EBP,
∴PB=PE,
∵点Q为线段BE的中点,
∴PQ⊥BC,
∴PQ∥AC
∴当PE∥CF时,四边形PDCF是平行四边形,
∴PF=CD,
当点P在边AB的上时,x=4﹣x,x=,
当点P在边AB的延长线上时,x=x﹣4,x=,
综上所述,当PE∥CF时,AP的长为或.
8.解:过点C作CE⊥AD于点E,
则AE=DE,
∵∠ACB=90°,AC=3,BC=4,
∴AB==5,
∵S△ABC=AC BC=AB CE,
∴CE==,
∴AE==,
∴AD=2AE=,
故答案为.
三.解答题
9.证明:过点O作OE⊥AB,
∵OA=OB,
∴AE=BE,
又∵在⊙O中,
∴CE=DE,
∴AC=BD
10.解:过点O作OM⊥CD于点M,联结OD,
∵∠CEA=30°,∴∠OEM=∠CEA=30°,
在Rt△OEM中,∵OE=4,
∴,,
∵,
∴,
∵OM过圆心,OM⊥CD,
∴CD=2DM,
∴,
∵,
∴在Rt△DOM中,,
∴弦CD的长为,⊙O的半径长为.
11.解:连接OA、OC,
∵由题意知:AB∥CD,OE⊥AB,OF⊥CD,CD=20cm,
∴CG=CD=10cm,
在Rt△OGC中,由勾股定理得:OC2=CG2+OG2,
OC2=102+(OC﹣2)2,
解得:OC=26(cm),
则OE=26cm﹣2cm﹣2cm=22cm,
∵在Rt△OEA中,由勾股定理得:OA2=OE2+AE2,
∴262=222+AE2,
∴AE=8,
∵OE⊥AB,OE过圆心O,
∴AB=2AE=16cm.
12.解:如图,假设船能通过,弧形桥所在的圆恢复如图,
在Rt△AOD中,r2=202+(r﹣10)2,
解得r=25,
∴OD=r﹣10=15,
在Rt△OEG中,r2=152+OG2,
解得OG=20,
∴可以通过的船的高度为GD=OG﹣OD=20﹣15=5,
∵6>5,
∴船不能通过.
13.解:过点O作OD⊥AB于点D,连接OA,
∵在Rt△ODC中,∠OCA=30°,OC=8cm,
∴OD=OC=4cm,
∵在Rt△OAD中,OA=5cm,
∴AD==3,
∴AB=2AD=6.
14.解:(1)作半径OD⊥AB于C,连接OB,
由垂径定理得:BC=AB=0.3,
在Rt△OBC中,OC==0.4
CD=0.5﹣0.4=0.1,
此时的水深为0.1米;
(2)当水位上升到圆心以下时 水面宽0.8 米
则OC==0.3,
水面上升的高度为:0.3﹣0.2=0.1米;
当水位上升到圆心以上时,水面上升的高度为:0.4+0.3=0.7米,
综上可得,水面上升的高度为 0.1米或 0.7米.
15.解:(1)连接OB.
∵OD过圆心,且D是弦BC中点,
∴OD⊥BC,BD=BC,
在Rt△BOD中,OD2+BD2=BO2.
∵BO=AO=8,BD=6.
∴OD=2;
(2)在Rt△EOD中,OD2+ED2=EO2.
设BE=x,则OE=x,DE=6﹣x.
(2)2+(6﹣x)2=(x)2,
解得x1=﹣16(舍),x2=4.
则DE=2.
16.解:作OP⊥CD于P,连接OD,
∴CP=PD,
∵AE=1,EB=5,
∴AB=6,
∴OE=2,
在Rt△OPE中,OP=OE sin∠DEB=,
∴PD==,
∴CD=2PD=2(cm).
17.解:分两种情况:
(i)当两条弦在圆心O异侧时,如图1所示:
过O作OE⊥AB,交CD于F点,
连接OB,OD,可得出OB=OD=5,
∵AB∥CD,∴EF⊥CD,
∴E为AB中点,F为CD中点,
又∵AB=6,CD=8,
∴EB=3,FD=4,
在Rt△OEB和Rt△ODF中,
利用勾股定理得:OE==4,OF==3,
则弦AB与CD间的距离EF=OE+OF=4+3=7;
(ii)当两条弦在圆心O同侧时,如图2所示:
同理求出OE=4,OF=3,
则弦AB与CD间的距离EF=OE﹣OF=4﹣3=1.
综上,弦AB与CD间的距离为1或7.
18.解:AC与BD是相等,理由如下;
过点O作OE⊥AB,
∵OA=OB,
∴AE=BE,
又∵在⊙O中,
∴CE=DE,
∴AC=BD.
19.解:(1)连接OD,
∵直径AB⊥弦CD,CD=4,
∴DH=CH=CD=2,
在Rt△ODH中,AH=5,
设圆O的半径为r,
根据勾股定理得:OD2=(AH﹣OA)2+DH2,即r2=(5﹣r)2+20,
解得:r=4.5,
则圆的半径为4.5;
(2)过O作OG⊥AE于G,
∴AG=AE=×6=3,
∵∠A=∠A,∠AGO=∠AHF,
∴AF=,
∴EF=AF﹣AE=﹣6=.
20.解:(1)∵CD⊥AB,AO⊥BC
∴∠AFO=∠CEO=90°,
在△AOF和△COE中,
,
∴△AOF≌△COE,
∴CE=AF,
∵CE=2,
∴AF=2,
∵CD是⊙O的直径,CD⊥AB,
∴,
∴AB=4.
(2)∵AO是⊙O的半径,AO⊥BC
∴CE=BE=2,
∵AB=4,
∴,
∵∠AEB=90°,
∴∠A=30°,
又∵∠AFO=90°,
∴,即⊙O的半径是.
21.解:(1)作法:分别作AB和AC的垂直平分线,设交点为O,则O为所求圆的圆心;
(2)连接AO、BO,AO交BC于E,
∵AB=AC,
∴AE⊥BC,
∴BE=BC=×8=4,
在Rt△ABE中,AE===3,
设⊙O的半径为R,在Rt△BEO中,
OB2=BE2+OE2,
即R2=42+(R﹣3)2,
R=,
答:圆片的半径R为cm.
22.解:(1)作OC⊥AB于点C,
∵圆心O到AB的距离为3,
∴OC=3,
∵弦AB的长为8,
∴AC=BC=4,
∴OA==5,
∴⊙O的半径为5;
(2)∵点P是AB上的一动点,
∴3≤PO≤5.
同课章节目录
