浙教版九年级数学下册 锐角三角函数课件2021-2022学年
文档属性
| 名称 | 浙教版九年级数学下册 锐角三角函数课件2021-2022学年 |  | |
| 格式 | zip | ||
| 文件大小 | 31.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-29 07:11:55 | ||
图片预览




文档简介
(共18张PPT)
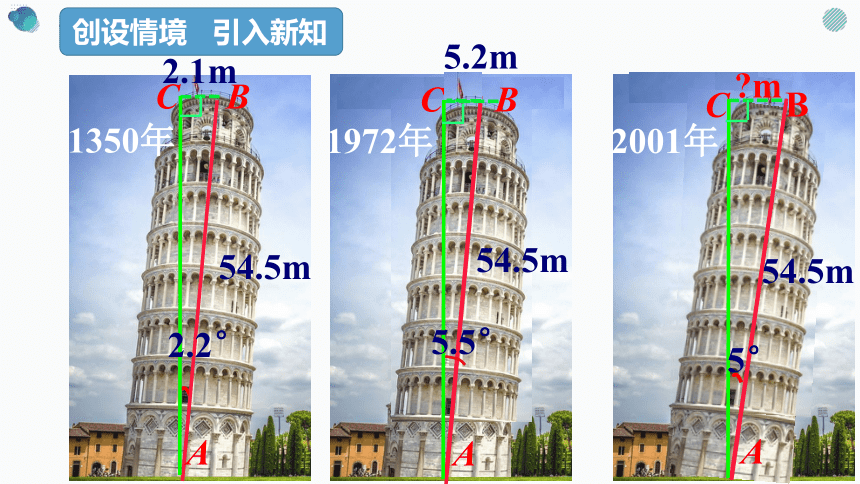
创设情境 引入新知
知道这是哪吗?
创设情境 引入新知
2.1m
54.5m
2.2°
C
A
B
5.2m
54.5m
C
A
B
54.5m
C
A
B
1350年
1972年
2001年
5.5°
5°
m
创设情境 引入新知
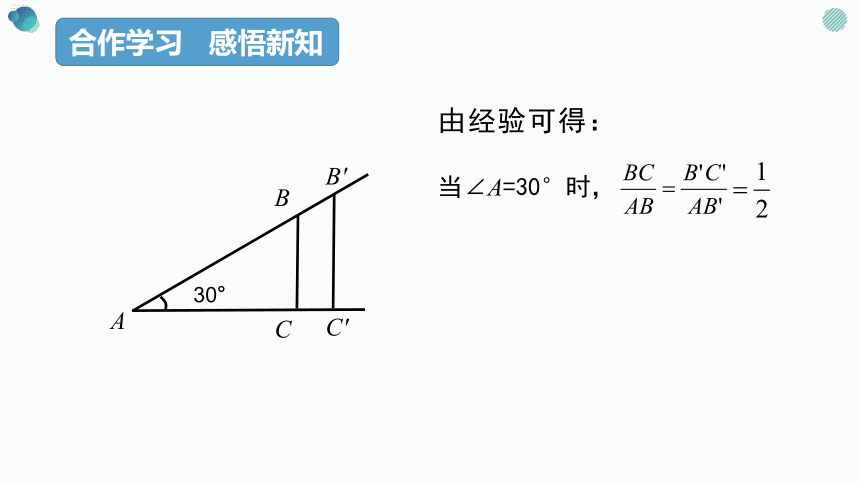
1.1锐角三角函数
A
B
C
B'
C'
合作学习 感悟新知
由经验可得:
30°
当∠A=30°时,
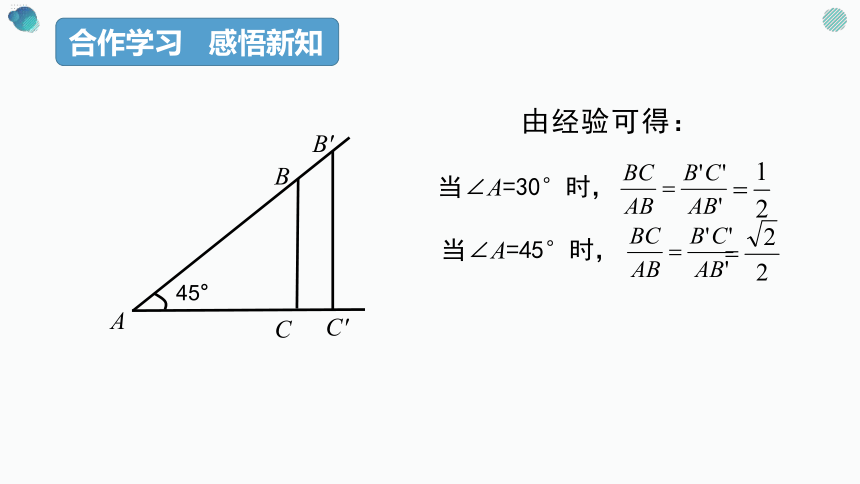
A
B
C
B'
C'
合作学习 感悟新知
由经验可得:
45°
当∠A=45°时,
当∠A=30°时,
A
B
C
B'
C'
合作学习 感悟新知
由经验可得:
60°
当∠A=45°时,
当∠A=30°时,
当∠A=60°时,
通过上面两个实践操作,你发现了什么?
合作学习 感悟新知
A
B
C
50°
A
B
C
15°
角度不变,比值不变
角度改变,比值改变
探究新知 明确定义
A
B
C
α
比值
叫做∠α的正弦值.
记做sinα.
正弦: sin A= ,如图,sin A=______.
余弦: cos A= ,如图,cos A=________.
正切: tan A= ,如图,tan A=________.
探究新知 明确定义
我们可以发现,锐角三角函数的值都是正实数,那么你知道sinA 和cosA 的取值范围吗?
0<cosA<1
0<sinA<1
A
B
C
如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,求∠A、∠B的正弦、余弦和正切.
5
3
4
例题学习 巩固概念
A
B
C
变式1.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,求∠B的正弦、余弦和正切.
6
8
变式练习 巩固概念
10
A
B
C
变式2.如图,在Rt△ABC中,∠C=90°,AC:BC=5:4,求∠B的正弦、余弦和正切.
4
5
变式练习 巩固概念
A
B
C
变式3.如图,在Rt△ABC中,∠C=90°, ,
求∠B的正弦、余弦和正切.
变式练习 巩固概念
5
3
4
A
B
C
变式4.如图,在Rt△ABC中,∠C=90°, ,
求∠BCD的正弦、余弦和正切.
变式练习 巩固概念
5
3
4
CD⊥AB,
D
4.905m
回归情景 巩固新知
归纳小结,反思提高
英文 名字 中文名字 三角形中的比例 取值
范围
a
c
b
c
a
b
sinA
cosA
tanA
∠A的正弦
∠A的余弦
∠A的正切
00tanA>0
A
B
C
归纳小结 反思提高
1.谈古论今,追根朔源 — 锐角三角函数的历史研究
2.书本作业题7
课后作业 巩固提升
创设情境 引入新知
知道这是哪吗?
创设情境 引入新知
2.1m
54.5m
2.2°
C
A
B
5.2m
54.5m
C
A
B
54.5m
C
A
B
1350年
1972年
2001年
5.5°
5°
m
创设情境 引入新知
1.1锐角三角函数
A
B
C
B'
C'
合作学习 感悟新知
由经验可得:
30°
当∠A=30°时,
A
B
C
B'
C'
合作学习 感悟新知
由经验可得:
45°
当∠A=45°时,
当∠A=30°时,
A
B
C
B'
C'
合作学习 感悟新知
由经验可得:
60°
当∠A=45°时,
当∠A=30°时,
当∠A=60°时,
通过上面两个实践操作,你发现了什么?
合作学习 感悟新知
A
B
C
50°
A
B
C
15°
角度不变,比值不变
角度改变,比值改变
探究新知 明确定义
A
B
C
α
比值
叫做∠α的正弦值.
记做sinα.
正弦: sin A= ,如图,sin A=______.
余弦: cos A= ,如图,cos A=________.
正切: tan A= ,如图,tan A=________.
探究新知 明确定义
我们可以发现,锐角三角函数的值都是正实数,那么你知道sinA 和cosA 的取值范围吗?
0<cosA<1
0<sinA<1
A
B
C
如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,求∠A、∠B的正弦、余弦和正切.
5
3
4
例题学习 巩固概念
A
B
C
变式1.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,求∠B的正弦、余弦和正切.
6
8
变式练习 巩固概念
10
A
B
C
变式2.如图,在Rt△ABC中,∠C=90°,AC:BC=5:4,求∠B的正弦、余弦和正切.
4
5
变式练习 巩固概念
A
B
C
变式3.如图,在Rt△ABC中,∠C=90°, ,
求∠B的正弦、余弦和正切.
变式练习 巩固概念
5
3
4
A
B
C
变式4.如图,在Rt△ABC中,∠C=90°, ,
求∠BCD的正弦、余弦和正切.
变式练习 巩固概念
5
3
4
CD⊥AB,
D
4.905m
回归情景 巩固新知
归纳小结,反思提高
英文 名字 中文名字 三角形中的比例 取值
范围
a
c
b
c
a
b
sinA
cosA
tanA
∠A的正弦
∠A的余弦
∠A的正切
0
A
B
C
归纳小结 反思提高
1.谈古论今,追根朔源 — 锐角三角函数的历史研究
2.书本作业题7
课后作业 巩固提升
