2.1算法的概念及描述 课件 2022—2023学年学年浙教版(2019)高中信息技术必修1(22张PPT)
文档属性
| 名称 | 2.1算法的概念及描述 课件 2022—2023学年学年浙教版(2019)高中信息技术必修1(22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-09-28 22:52:07 | ||
图片预览






文档简介
(共22张PPT)
2.1
算法的概念及描述
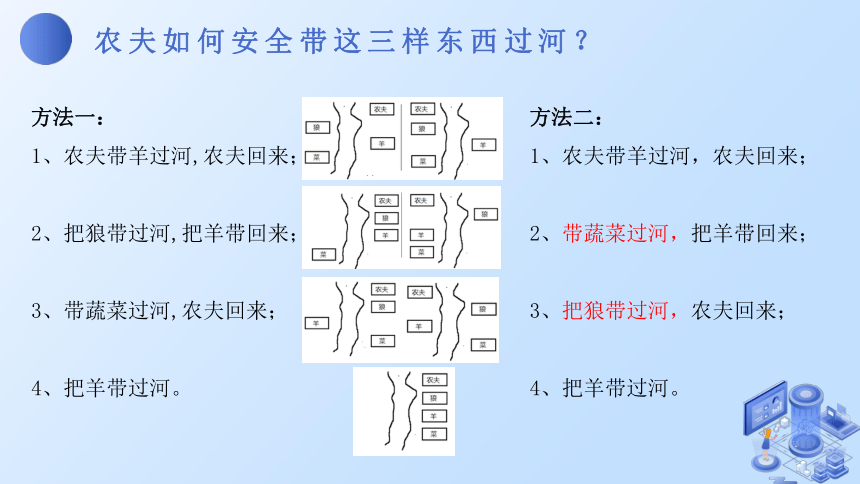
农夫如何安全带这三样东西过河?
一个农夫带着一条狼、一头山羊和一篮蔬菜要过河,但只有一条船。乘船时,农夫在场的时候,这三样东西相安无事。一旦农夫不在,狼会吃羊,羊会吃菜。船很小,只够农夫带一样东西过河。农夫该如何解此难题?
方法一:
1、农夫带羊过河,农夫回来;
2、把狼带过河,把羊带回来;
3、带蔬菜过河,农夫回来;
4、把羊带过河。
方法二:
1、农夫带羊过河,农夫回来;
2、带蔬菜过河,把羊带回来;
3、把狼带过河,农夫回来;
4、把羊带过河。
农夫如何安全带这三样东西过河?
2.1.1 算法的概念
广义:“算法”指的是解决问题或完成任务的一系列步骤。
不仅仅指计算任务(算术),也可以是社会生活中各种事务的处理。
计算机科学领域:“算法”指的是用计算机解决问题的步骤,是为了解决问题而需要让计算机有序执行的、无歧义的、有限步骤的集合。
不仅包含了数值计算,还包含了非数值计算的数据处理。
1. 算法的定义
为了让计算机理解算法中的步骤,用计算机能理解的语言来描述算法并将其输入到计算机中,这个过程就称为计算机程序设计。
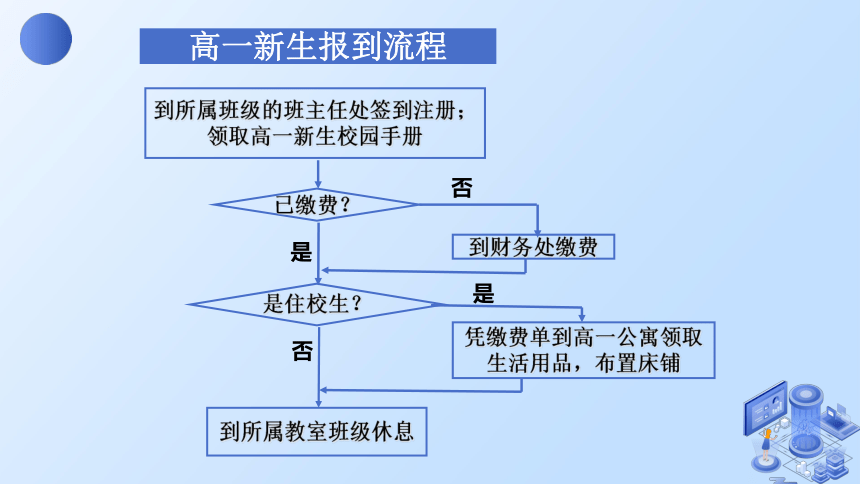
到所属班级的班主任处签到注册;
领取高一新生校园手册
已缴费?
是住校生?
到所属教室班级休息
到财务处缴费
凭缴费单到高一公寓领取生活用品,布置床铺
否
否
是
是
高一新生报到流程
例:用求根公式求解一元二次方程的算法
一元二次方程的解的意义:能使一元二次方程左右两边相等的未知数的值称为一元二次方程的解。利用一元二次方程根的判别式( )可以判断方程的根的情况。
过程方法具体描述: ax +bx+c=0
(1)输入一般形式下的二次项系数a,一次项系数b,常数项c;
(2)计算判别式 的值;
(3)若 ,则计算 ,输出字符串“方程有实数解”,并输出x的值;否则,输出字符串“方程无实数解”。
特征 含义
有穷性 一个算法的处理步骤必须是有限的
可行性 一个算法中的每一步操作与要求都应该是算法执行者(人或机器)可以实施的,同时在现实环境中能做到并且能在有限时间内完成
确定性 算法中对于每个步骤的执行描述必须是明确的
0个或多个输入 数据可从外部输入,也可包含在算法中(可以没有输入)
1个或多个输出 算法必须包含至少一个输出,以告诉外界问题求解的结果(必须有输出)
2. 算法的特征
把大象放冰箱是不是算法?
不是算法,不满足算法的可行性。
农夫过河是不是算法?
是算法。
思考:
求根公式求解一元二次方程的算法:
(1)输入一般形式下的二次项系数a,一次项系数b,常数项c
(2)计算判别式 的值
(3)若 ,则计算 ,输出字符串“方程有实数解”,并输
出x的值;否则,输出字符串“方程无实数解”
要素 含义
数据 明确参与运算的初始数据、运算时产生的中间数据以及代表问题解决的结果数据
运算 明确每一步的运算是什么、对哪些数据进行运算等
控制转移 有时需要根据数据或运算结果的特点进行不同的处理,这时就需要运用控制转移来执行不同的操作
3. 算法的要素
a,b,c, ,x
加减乘除,
开根,平方
若......,则......;
否则........
2.1.2 算法的描述
设计出一个解决问题的算法,也需要用能被算法执行者理解的形式加以呈现,才能被算法执行者(人或计算机)理解并执行。算法的这种呈现就称为算法的描述。
常见的算法描述方式有自然语言、流程图、伪代码、计算机程序设计语言等。
2.1.2 算法的描述
自然语言是人们在日常生活中交流使用的语言,如汉语、英语、德语、日语等。用自然语言描述算法通俗易懂,且不需要进行专门的学习和训练。
阅读:停车场车位探测中的算法,尝试用自然语言描述该算法。
自然语言描述如下:
(1)输入变量flag的值。
(2)若flag的值为1, 则设置指示灯为绿色,输出“空车位”;否则,设置指示灯为红色,输出“非空车位。
1. 自然语言描述算法
流程图用一些图形符号表示规定的操作,并用带箭头的流程线连接这些图形符号,表示操作进行方向。
2. 流程图描述算法
自然语言描述如下:
(1)输入变量flag的值。
(2)若flag的值为1, 则设置指示灯为绿色,输出“空车位”;否则,设置指示灯为红色,输出“非空车位。
2. 流程图描述算法
图形 名称 功能
开始/结束框 表示算法的开始或结束
输入/输出框 表示算法中数据的输入或输出
处理框 表示算法中数据的运算处理
判断框 表示算法中的条件判断
流程线 表示算法中的流向
连接框 表示算法中的转接
尝试画出求根公式的流程图
2. 流程图描述算法
开始
输入二项系数a,
一项系数b,常数c
计算判别式
?
计算
输出方程
无实数根
输出方程有实数根
输出x
结束
否
是
“N-S图”是由美国学者纳西(Nassi)和斯奈德曼(Shneiderman)提出的一种在流程图中完全去掉流程线,全部算法写在一个矩形框内的算法描述方式。相比于原来的流程图描述,结构性显得更好,也更有助于高效地编写程序。前面车位探测中的算法,可用N-S图表示成如下形式。
输入flag的值 指示灯绿色 指示灯红色
输出“空车位” 输出“非空车位”
flag=1
是
否
拓展链接
伪代码指的是一种比较直观简洁的、符号接近计算机程序代码的算法描述方式,其风格很像计算机程序设计语言,但又不是真正的可以被计算机理解的代码。
求根公式算法
3. 伪代码描述算法
格式1: If 条件 then
(语句序列1)
Else
(语句序列2)
格式2: If 条件 then
(语句序列1)
条件判断语句
格式:while 条件
(循环体)
循环语句
车位探测算法
flag←车位探测结果;
If flag=1 then
(指示灯绿色
输出“空车位”)
Else
(指示灯红色
输出“非空车位”)
为了让计算机真正解决问题,需要将算法用某种计算机程序设计语言来描述,这个过程称为程序编写(或称代码编写)。
4. 计算机程序语言描述算法
车位探测算法
flag=int(input(“输入车位状态值:”))
if flag==1:
print(“绿色”)
print(“空车位”)
else:
print(“红色”)
print(“非空车位”)
求根公式算法
a=int(input(“输入二次项系数:”))
b=int(input(“输入一次项系数:”))
c=int(input(“输入常数项系数:”))
ref=b**2-4*a*c
if ref>=0:
x1=((-b)+math.sqrt(ref))/(2*a)
x2=((-b)-math.sqrt(ref))/(2*a)
printf(“方程有实数解”)
printf(“x1=”,x1)
printf(“x2=”,x2)
else:
printf(“方程无实数解”)
求两个正整数的最大公约数问题
(1)输入两个正整数m和n。
(2)若m(3)以m除以n,相除得到的余数为r。
(4)若r = 0,则输出n的值,算法结束;
否则,执行步骤(5)。
(5)令m = n, n = r,返回步骤(3)继续执行。
辗转相除法
更相减损术
(1)输入两个正整数m和n。
(2)判断两个数是否都是偶数,若是,则用2约简,直至出现奇数。
(3)以较大的数(被减数)减去较小的数(减数),得到差。
(4)若减数与差相等,则第二步约掉的若干个2与差的乘积就是最大公约数,算法结束;否则,执行步骤(5)。
(5)将减数与差作为比较的数,返回步骤(3)继续执行。
体验算法多样性
1.算法的概念
解决问题或完成任务的一系列步骤;
为了解决问题而需要让计算机有序执行的、无歧义的、有限步骤的集合
2.算法的特征
有穷性;可行性;确定性;0个或多个输入;1个或多个输出
3.算法的要素
数据,运算,控制转移
4.算法的描述
自然语言、流程图、伪代码、计算机程序设计语言
小结
《作业本》
P29-32
作业
2.1
算法的概念及描述
农夫如何安全带这三样东西过河?
一个农夫带着一条狼、一头山羊和一篮蔬菜要过河,但只有一条船。乘船时,农夫在场的时候,这三样东西相安无事。一旦农夫不在,狼会吃羊,羊会吃菜。船很小,只够农夫带一样东西过河。农夫该如何解此难题?
方法一:
1、农夫带羊过河,农夫回来;
2、把狼带过河,把羊带回来;
3、带蔬菜过河,农夫回来;
4、把羊带过河。
方法二:
1、农夫带羊过河,农夫回来;
2、带蔬菜过河,把羊带回来;
3、把狼带过河,农夫回来;
4、把羊带过河。
农夫如何安全带这三样东西过河?
2.1.1 算法的概念
广义:“算法”指的是解决问题或完成任务的一系列步骤。
不仅仅指计算任务(算术),也可以是社会生活中各种事务的处理。
计算机科学领域:“算法”指的是用计算机解决问题的步骤,是为了解决问题而需要让计算机有序执行的、无歧义的、有限步骤的集合。
不仅包含了数值计算,还包含了非数值计算的数据处理。
1. 算法的定义
为了让计算机理解算法中的步骤,用计算机能理解的语言来描述算法并将其输入到计算机中,这个过程就称为计算机程序设计。
到所属班级的班主任处签到注册;
领取高一新生校园手册
已缴费?
是住校生?
到所属教室班级休息
到财务处缴费
凭缴费单到高一公寓领取生活用品,布置床铺
否
否
是
是
高一新生报到流程
例:用求根公式求解一元二次方程的算法
一元二次方程的解的意义:能使一元二次方程左右两边相等的未知数的值称为一元二次方程的解。利用一元二次方程根的判别式( )可以判断方程的根的情况。
过程方法具体描述: ax +bx+c=0
(1)输入一般形式下的二次项系数a,一次项系数b,常数项c;
(2)计算判别式 的值;
(3)若 ,则计算 ,输出字符串“方程有实数解”,并输出x的值;否则,输出字符串“方程无实数解”。
特征 含义
有穷性 一个算法的处理步骤必须是有限的
可行性 一个算法中的每一步操作与要求都应该是算法执行者(人或机器)可以实施的,同时在现实环境中能做到并且能在有限时间内完成
确定性 算法中对于每个步骤的执行描述必须是明确的
0个或多个输入 数据可从外部输入,也可包含在算法中(可以没有输入)
1个或多个输出 算法必须包含至少一个输出,以告诉外界问题求解的结果(必须有输出)
2. 算法的特征
把大象放冰箱是不是算法?
不是算法,不满足算法的可行性。
农夫过河是不是算法?
是算法。
思考:
求根公式求解一元二次方程的算法:
(1)输入一般形式下的二次项系数a,一次项系数b,常数项c
(2)计算判别式 的值
(3)若 ,则计算 ,输出字符串“方程有实数解”,并输
出x的值;否则,输出字符串“方程无实数解”
要素 含义
数据 明确参与运算的初始数据、运算时产生的中间数据以及代表问题解决的结果数据
运算 明确每一步的运算是什么、对哪些数据进行运算等
控制转移 有时需要根据数据或运算结果的特点进行不同的处理,这时就需要运用控制转移来执行不同的操作
3. 算法的要素
a,b,c, ,x
加减乘除,
开根,平方
若......,则......;
否则........
2.1.2 算法的描述
设计出一个解决问题的算法,也需要用能被算法执行者理解的形式加以呈现,才能被算法执行者(人或计算机)理解并执行。算法的这种呈现就称为算法的描述。
常见的算法描述方式有自然语言、流程图、伪代码、计算机程序设计语言等。
2.1.2 算法的描述
自然语言是人们在日常生活中交流使用的语言,如汉语、英语、德语、日语等。用自然语言描述算法通俗易懂,且不需要进行专门的学习和训练。
阅读:停车场车位探测中的算法,尝试用自然语言描述该算法。
自然语言描述如下:
(1)输入变量flag的值。
(2)若flag的值为1, 则设置指示灯为绿色,输出“空车位”;否则,设置指示灯为红色,输出“非空车位。
1. 自然语言描述算法
流程图用一些图形符号表示规定的操作,并用带箭头的流程线连接这些图形符号,表示操作进行方向。
2. 流程图描述算法
自然语言描述如下:
(1)输入变量flag的值。
(2)若flag的值为1, 则设置指示灯为绿色,输出“空车位”;否则,设置指示灯为红色,输出“非空车位。
2. 流程图描述算法
图形 名称 功能
开始/结束框 表示算法的开始或结束
输入/输出框 表示算法中数据的输入或输出
处理框 表示算法中数据的运算处理
判断框 表示算法中的条件判断
流程线 表示算法中的流向
连接框 表示算法中的转接
尝试画出求根公式的流程图
2. 流程图描述算法
开始
输入二项系数a,
一项系数b,常数c
计算判别式
?
计算
输出方程
无实数根
输出方程有实数根
输出x
结束
否
是
“N-S图”是由美国学者纳西(Nassi)和斯奈德曼(Shneiderman)提出的一种在流程图中完全去掉流程线,全部算法写在一个矩形框内的算法描述方式。相比于原来的流程图描述,结构性显得更好,也更有助于高效地编写程序。前面车位探测中的算法,可用N-S图表示成如下形式。
输入flag的值 指示灯绿色 指示灯红色
输出“空车位” 输出“非空车位”
flag=1
是
否
拓展链接
伪代码指的是一种比较直观简洁的、符号接近计算机程序代码的算法描述方式,其风格很像计算机程序设计语言,但又不是真正的可以被计算机理解的代码。
求根公式算法
3. 伪代码描述算法
格式1: If 条件 then
(语句序列1)
Else
(语句序列2)
格式2: If 条件 then
(语句序列1)
条件判断语句
格式:while 条件
(循环体)
循环语句
车位探测算法
flag←车位探测结果;
If flag=1 then
(指示灯绿色
输出“空车位”)
Else
(指示灯红色
输出“非空车位”)
为了让计算机真正解决问题,需要将算法用某种计算机程序设计语言来描述,这个过程称为程序编写(或称代码编写)。
4. 计算机程序语言描述算法
车位探测算法
flag=int(input(“输入车位状态值:”))
if flag==1:
print(“绿色”)
print(“空车位”)
else:
print(“红色”)
print(“非空车位”)
求根公式算法
a=int(input(“输入二次项系数:”))
b=int(input(“输入一次项系数:”))
c=int(input(“输入常数项系数:”))
ref=b**2-4*a*c
if ref>=0:
x1=((-b)+math.sqrt(ref))/(2*a)
x2=((-b)-math.sqrt(ref))/(2*a)
printf(“方程有实数解”)
printf(“x1=”,x1)
printf(“x2=”,x2)
else:
printf(“方程无实数解”)
求两个正整数的最大公约数问题
(1)输入两个正整数m和n。
(2)若m
(4)若r = 0,则输出n的值,算法结束;
否则,执行步骤(5)。
(5)令m = n, n = r,返回步骤(3)继续执行。
辗转相除法
更相减损术
(1)输入两个正整数m和n。
(2)判断两个数是否都是偶数,若是,则用2约简,直至出现奇数。
(3)以较大的数(被减数)减去较小的数(减数),得到差。
(4)若减数与差相等,则第二步约掉的若干个2与差的乘积就是最大公约数,算法结束;否则,执行步骤(5)。
(5)将减数与差作为比较的数,返回步骤(3)继续执行。
体验算法多样性
1.算法的概念
解决问题或完成任务的一系列步骤;
为了解决问题而需要让计算机有序执行的、无歧义的、有限步骤的集合
2.算法的特征
有穷性;可行性;确定性;0个或多个输入;1个或多个输出
3.算法的要素
数据,运算,控制转移
4.算法的描述
自然语言、流程图、伪代码、计算机程序设计语言
小结
《作业本》
P29-32
作业
