第3章 圆的基本性质复习课件
图片预览



文档简介
课件17张PPT。一叶知秋窥一斑而知全豹圆的基本性质复习一
联 想 转化 法
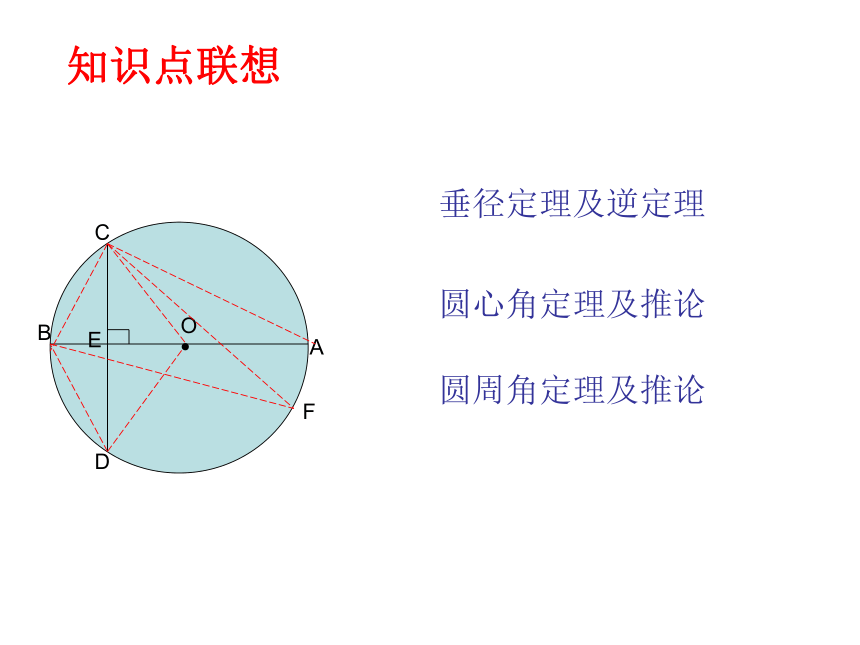
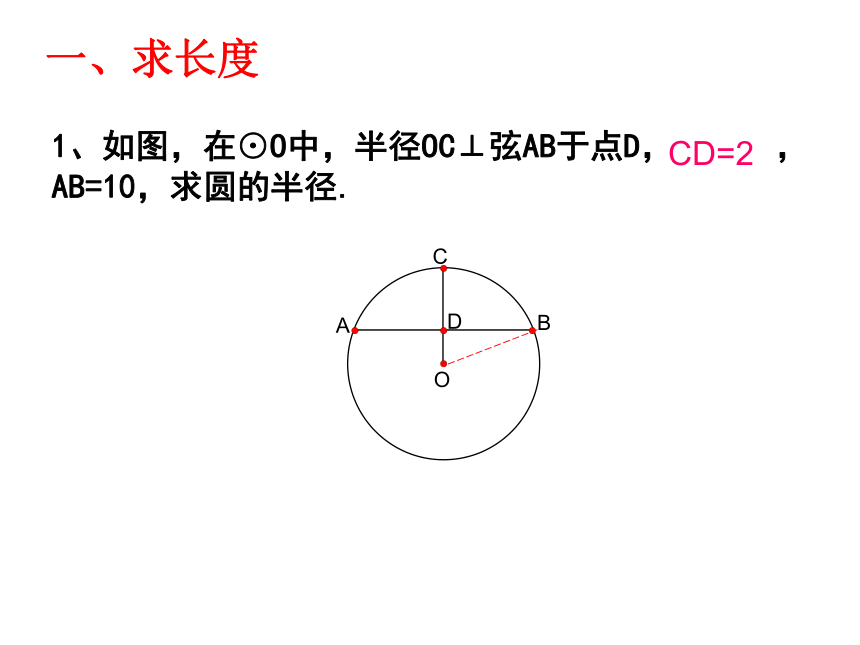
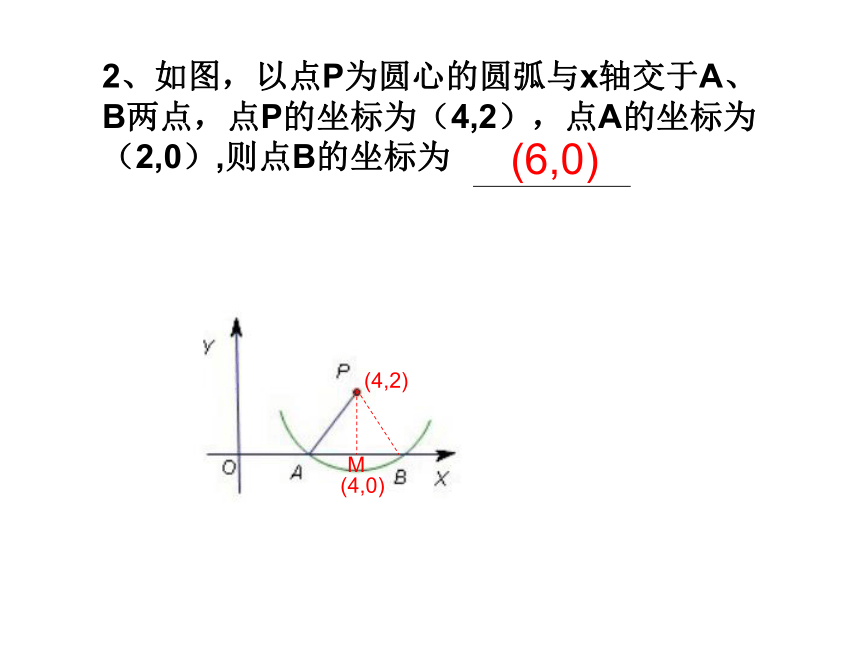
OAB●知识点联想垂径定理及逆定理圆心角定理及推论圆周角定理及推论1、如图,在⊙O中,半径OC⊥弦AB于点D,OD=2 ,AB=10,求圆的半径.一、求长度CD=2M(4,2)(4,0)(6,0)2、如图,以点P为圆心的圆弧与x轴交于A、B两点,点P的坐标为(4,2),点A的坐标为(2,0),则点B的坐标为
3、如图,在⊙O中,弦AC=BC,∠A=50°,求∠AOC、∠B、∠ACB的度数。二、算角度D3.6 cm4、如图,在圆O中,弦AB=1.8cm,圆周角∠ACB=30°,则圆O的直径为多少?
三、长度与角度的转化 5、已知⊙O中弦AB的长等于半径,
求弦AB所对的圆心角和圆周角的度数。 圆心角为60度圆周角为 30 度或 150 度。圆中
多解
问题 6、如图已知A、B、C、D、E均在圆O上,且AC 为圆O的直径,求∠A+∠B+∠C的度数。 1、如图,AB为⊙O的直径,CD为弦,且CD AB,垂足为H.
若∠OCD 的平分线CE交⊙O 于点E,连结OE.
求证:E为弧ADB的中点;CABEDOH四、综合应用(2)如图所示⌒=60°, G是⌒的中点,若⊙O的直径
AB=10, 问:在AB上是否存在点P使得PC+PG最短?若
存在,求出最短距离;若不存在,请说明理由.BC●●●ABCG●PG’BC(3)点C所在位置如图所示,此时在⌒上有一点G,
若⊙O的直径AB=10,点C、G到AB的距离分别是4和3,
问:在AB上是否存在点P使得PC+PG最短?若存在,求出最短距离;若不存在,请说明理由.BC●●●ABCG●PC’H条 件 是 点
知 识 是 线
联 想 转 化
串 成 一 片
五、谈谈收获祝同学们解题顺利轻松2、如图,在⊙O中,两条弦AC,BD垂直相交于点M,若AB=6,CD=8,求⊙O的半径。 E五、拓展提高C3.△ABC内接于⊙O,P为弧AC的中点,PQ//AB,点Q在BC上,QR//PA,点R在AB上, 求证:AR=BQD
联 想 转化 法
OAB●知识点联想垂径定理及逆定理圆心角定理及推论圆周角定理及推论1、如图,在⊙O中,半径OC⊥弦AB于点D,OD=2 ,AB=10,求圆的半径.一、求长度CD=2M(4,2)(4,0)(6,0)2、如图,以点P为圆心的圆弧与x轴交于A、B两点,点P的坐标为(4,2),点A的坐标为(2,0),则点B的坐标为
3、如图,在⊙O中,弦AC=BC,∠A=50°,求∠AOC、∠B、∠ACB的度数。二、算角度D3.6 cm4、如图,在圆O中,弦AB=1.8cm,圆周角∠ACB=30°,则圆O的直径为多少?
三、长度与角度的转化 5、已知⊙O中弦AB的长等于半径,
求弦AB所对的圆心角和圆周角的度数。 圆心角为60度圆周角为 30 度或 150 度。圆中
多解
问题 6、如图已知A、B、C、D、E均在圆O上,且AC 为圆O的直径,求∠A+∠B+∠C的度数。 1、如图,AB为⊙O的直径,CD为弦,且CD AB,垂足为H.
若∠OCD 的平分线CE交⊙O 于点E,连结OE.
求证:E为弧ADB的中点;CABEDOH四、综合应用(2)如图所示⌒=60°, G是⌒的中点,若⊙O的直径
AB=10, 问:在AB上是否存在点P使得PC+PG最短?若
存在,求出最短距离;若不存在,请说明理由.BC●●●ABCG●PG’BC(3)点C所在位置如图所示,此时在⌒上有一点G,
若⊙O的直径AB=10,点C、G到AB的距离分别是4和3,
问:在AB上是否存在点P使得PC+PG最短?若存在,求出最短距离;若不存在,请说明理由.BC●●●ABCG●PC’H条 件 是 点
知 识 是 线
联 想 转 化
串 成 一 片
五、谈谈收获祝同学们解题顺利轻松2、如图,在⊙O中,两条弦AC,BD垂直相交于点M,若AB=6,CD=8,求⊙O的半径。 E五、拓展提高C3.△ABC内接于⊙O,P为弧AC的中点,PQ//AB,点Q在BC上,QR//PA,点R在AB上, 求证:AR=BQD
同课章节目录
