3.2 不等式的基本性质 课件(共21张PPT)
文档属性
| 名称 | 3.2 不等式的基本性质 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-05 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
3.2 不等式的基本性质
浙教版 八年级上册
教学目标
【教学目标】
1.掌握和理解不等式的三条基本性质.
2.培养学生观察、分析和比较的能力,会运用不等式的基本性质进行不等式的变形,提高他们灵活地运用所学知识解题的能力.
【重点】不等式的三条基本性质的运用.
【难点】不等式的基本性质3的运用和不等式的变形以及范例要比较两个代数式的大小的几种方法,是本节教学的难点.
前面我们已经学习过等式的基本性质
(1)等式两边加(或减去)同一个数(或式子),
结果仍相等.
(2)等式两边乘同一个数,或除以同一个不为0的数,
结果仍相等.
猜想 :不等式也具有同样的性质吗?
复习导入
合作学习
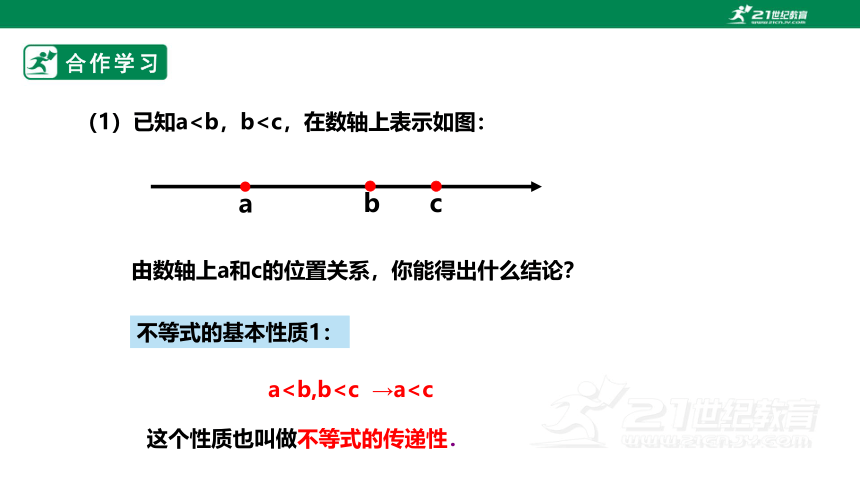
(1)已知aa
b
c
由数轴上a和c的位置关系,你能得出什么结论?
这个性质也叫做不等式的传递性.
a不等式的基本性质1:
合作学习
b
a
b+c
a+c
c
c
b-c
a-c
b
a
c
c
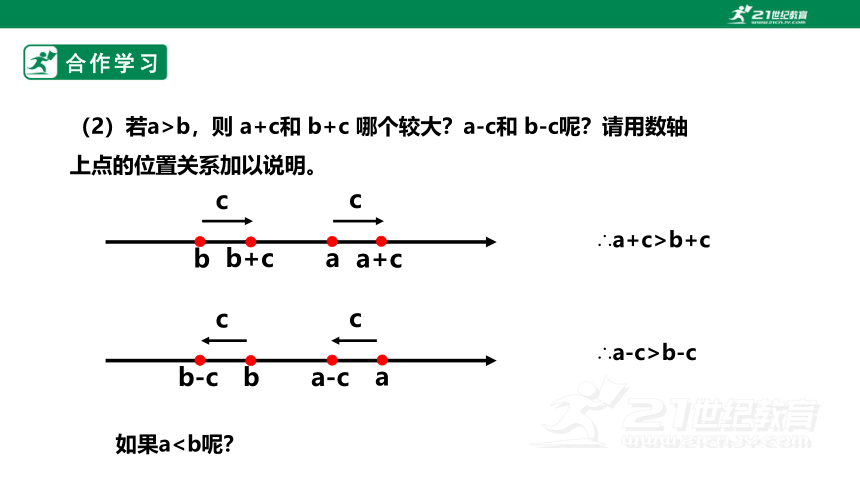
∴a+c>b+c
∴a-c>b-c
如果a(2)若a>b,则 a+c和 b+c 哪个较大?a-c和 b-c呢?请用数轴上点的位置关系加以说明。
合作学习
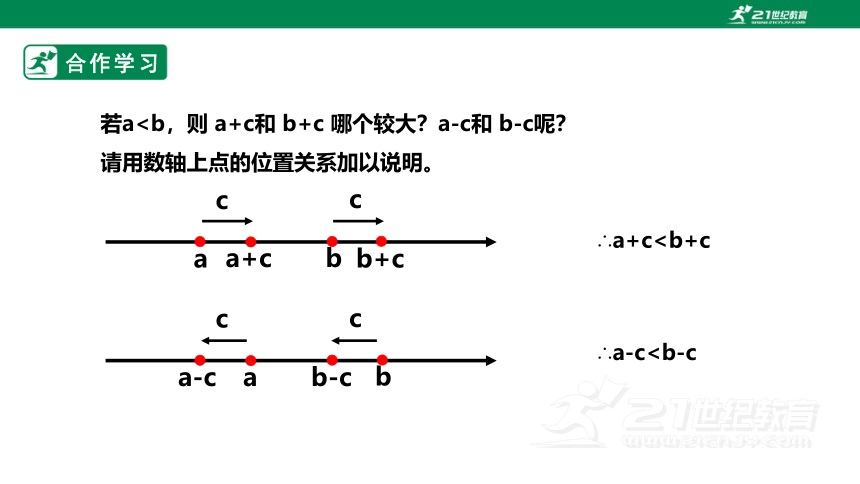
若aa
b
a+c
b+c
c
c
a-c
b-c
a
b
c
c
∴a+c∴a-c归纳总结
如果a>b,那么a+c>b+c,a-c>b-c;
如果a<b,那么a+c<b+c,a-c<b-c.
不等式的基本性质2:
不等式的两边都加上(或减去)同一个数,所得到的不等式仍成立.
做一做
选择适当的不等号填空:
(1) ∵ 0 1,
∴ a a+1(不等式的基本性质2)
(2) ∵ (a-1) 0,
∴ (a-1) -2 -2(不等式的基本性质2)
<
<
≥
≥
你有什么发现吗?
8 12
8×4 12×4
8÷3 12÷3
<
(–4) (– 6)
(– 4)×(–2) (– 6)×(–2)
(– 4)÷(–4) (– 6)÷(–4)
<
<
<
比较大小:
不等式的两边都乘以(或除以)同一个正数, 所得的不等式仍成立;
不等式的两边都乘以(或除以)同一个负数,必须把不等号的方向改变,所得的不等式成立;
<
<
合作探究
1、不等式的两边都乘以(或除以)同一个正数,所得的不等式仍成立;(正数不变向)
2、不等式的两边都乘以(或除以)同一个负数,必须把不等号的方向改变,所得的不等式成立. (负数要变向)
不等式的基本性质3
口诀记忆法:
加减方向不变
乘除正数方向也不变
乘除负数方向要改变
不等号方向改变
归纳总结
针对训练
用适当的不等号填空:
(1)若 a-1(2)若 -3a<-3b,则 a____b;
(3)若 0.3a+1<0.3b+1,则 a___b.
<
>
<
两边同时加1
两边同时除以-3
0.3a<0.3b
a两边同时减1
两边同时除以0.3
例题讲解
例 已知a<0,试比较2a与a的大小.
解法一:∵2>1,a<0,
∴2a<a(不等式的基本性质3)
解法二:在数轴上分别表示2a和a的点(a<0),如图. 2a位于a的左边,所以2a<a.
0
a
2a
∣a∣
∣a∣
例题讲解
例 已知a<0 ,试比较2a与a的大小.
解法三:∵ a<0,
∴ a+a<a
∴2a课堂练习
1.(1)若x+1>0,两边同加上-1,
得_________ (依据:_______________________ );
(2)若2x>-6,两边同除以2,
得_________ (依据:_______________________ );
(3)若 x≤ ,两边同乘 -3,
得 _________ (依据:__________________________).
x>-1
不等式的基本性质2
不等式的基本性质3
x≥
x>-3
不等式的基本性质3
课堂练习
2.若 m>n,则下列不等式不一定成立的是( )
A. m+3>n+3
B. -3m<-3n
C.
D. m2>n2
加同一个数,不等号方向不变
除以同一个正数,不等号方向不变
乘同一个负数,不等号方向改变
当 m=2,n=-3 时,m2D
课堂练习
3. 已知a < b,用“>”或“<”填空:
(1)a +12 b +12 ;
(2)b-10 a -10 .
<
>
4.由x<y得到ax<ay,则a应满足条件是( )
A.a≥0 B.a≤0
C.a>0 D.a<0
C
课堂练习
5.将物体“▲”的质量用 a 表示,物体“●”的质量用 b 表示,现已知 ab+a
a+a
两边同时加 aa+aB
课堂练习
6.若实数 a,b,c 在数轴上的位置如图所示,则下列不等式成立的是( )
A. abB. ac>bc
C. a+c>b+c
D. a+bc<0c0
acaac>bc
b>a,c<0
b+c>a+c
a>c,b>0
a+b>c+b
B
课堂总结
不等式的基本性质
性质1:若a<b,b<c,则a<c。
性质2:不等式的两边都加上(或减去)同一个数,所得到的不等式仍成立.
性质3:
不等式的两边都乘(或都除以)同一个正数,所得到的不等式仍成立;
不等式的两边都乘(或都除以)同一个负数,必须把不等号的方向改变,所得到的不等式成立.
(传递性)
(不等号方向不变)
(不等号方向不变)
(不等号方向改变)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.2 不等式的基本性质
浙教版 八年级上册
教学目标
【教学目标】
1.掌握和理解不等式的三条基本性质.
2.培养学生观察、分析和比较的能力,会运用不等式的基本性质进行不等式的变形,提高他们灵活地运用所学知识解题的能力.
【重点】不等式的三条基本性质的运用.
【难点】不等式的基本性质3的运用和不等式的变形以及范例要比较两个代数式的大小的几种方法,是本节教学的难点.
前面我们已经学习过等式的基本性质
(1)等式两边加(或减去)同一个数(或式子),
结果仍相等.
(2)等式两边乘同一个数,或除以同一个不为0的数,
结果仍相等.
猜想 :不等式也具有同样的性质吗?
复习导入
合作学习
(1)已知a
b
c
由数轴上a和c的位置关系,你能得出什么结论?
这个性质也叫做不等式的传递性.
a
合作学习
b
a
b+c
a+c
c
c
b-c
a-c
b
a
c
c
∴a+c>b+c
∴a-c>b-c
如果a
合作学习
若a
b
a+c
b+c
c
c
a-c
b-c
a
b
c
c
∴a+c
如果a>b,那么a+c>b+c,a-c>b-c;
如果a<b,那么a+c<b+c,a-c<b-c.
不等式的基本性质2:
不等式的两边都加上(或减去)同一个数,所得到的不等式仍成立.
做一做
选择适当的不等号填空:
(1) ∵ 0 1,
∴ a a+1(不等式的基本性质2)
(2) ∵ (a-1) 0,
∴ (a-1) -2 -2(不等式的基本性质2)
<
<
≥
≥
你有什么发现吗?
8 12
8×4 12×4
8÷3 12÷3
<
(–4) (– 6)
(– 4)×(–2) (– 6)×(–2)
(– 4)÷(–4) (– 6)÷(–4)
<
<
<
比较大小:
不等式的两边都乘以(或除以)同一个正数, 所得的不等式仍成立;
不等式的两边都乘以(或除以)同一个负数,必须把不等号的方向改变,所得的不等式成立;
<
<
合作探究
1、不等式的两边都乘以(或除以)同一个正数,所得的不等式仍成立;(正数不变向)
2、不等式的两边都乘以(或除以)同一个负数,必须把不等号的方向改变,所得的不等式成立. (负数要变向)
不等式的基本性质3
口诀记忆法:
加减方向不变
乘除正数方向也不变
乘除负数方向要改变
不等号方向改变
归纳总结
针对训练
用适当的不等号填空:
(1)若 a-1
(3)若 0.3a+1<0.3b+1,则 a___b.
<
>
<
两边同时加1
两边同时除以-3
0.3a<0.3b
a
两边同时除以0.3
例题讲解
例 已知a<0,试比较2a与a的大小.
解法一:∵2>1,a<0,
∴2a<a(不等式的基本性质3)
解法二:在数轴上分别表示2a和a的点(a<0),如图. 2a位于a的左边,所以2a<a.
0
a
2a
∣a∣
∣a∣
例题讲解
例 已知a<0 ,试比较2a与a的大小.
解法三:∵ a<0,
∴ a+a<a
∴2a
1.(1)若x+1>0,两边同加上-1,
得_________ (依据:_______________________ );
(2)若2x>-6,两边同除以2,
得_________ (依据:_______________________ );
(3)若 x≤ ,两边同乘 -3,
得 _________ (依据:__________________________).
x>-1
不等式的基本性质2
不等式的基本性质3
x≥
x>-3
不等式的基本性质3
课堂练习
2.若 m>n,则下列不等式不一定成立的是( )
A. m+3>n+3
B. -3m<-3n
C.
D. m2>n2
加同一个数,不等号方向不变
除以同一个正数,不等号方向不变
乘同一个负数,不等号方向改变
当 m=2,n=-3 时,m2
课堂练习
3. 已知a < b,用“>”或“<”填空:
(1)a +12 b +12 ;
(2)b-10 a -10 .
<
>
4.由x<y得到ax<ay,则a应满足条件是( )
A.a≥0 B.a≤0
C.a>0 D.a<0
C
课堂练习
5.将物体“▲”的质量用 a 表示,物体“●”的质量用 b 表示,现已知 a
a+a
两边同时加 aa+a
课堂练习
6.若实数 a,b,c 在数轴上的位置如图所示,则下列不等式成立的是( )
A. ab
C. a+c>b+c
D. a+b
ac
b>a,c<0
b+c>a+c
a>c,b>0
a+b>c+b
B
课堂总结
不等式的基本性质
性质1:若a<b,b<c,则a<c。
性质2:不等式的两边都加上(或减去)同一个数,所得到的不等式仍成立.
性质3:
不等式的两边都乘(或都除以)同一个正数,所得到的不等式仍成立;
不等式的两边都乘(或都除以)同一个负数,必须把不等号的方向改变,所得到的不等式成立.
(传递性)
(不等号方向不变)
(不等号方向不变)
(不等号方向改变)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
