3.1 认识不等式 课件(共24张PPT)
文档属性
| 名称 | 3.1 认识不等式 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-05 16:12:29 | ||
图片预览







文档简介
(共24张PPT)
3.1 认识不等式
浙教版 八年级上册
教学目标
【教学目标】
1.了解不等式的意义,经历由具体实例建立不等式模型的过程。
2.了解不等号的意义。
3.会根据给定的条件列不等式。
【重点】不等式的概念和列不等式。
【难点】既要理解不等式的意义,又要会在数轴上表示,并用来解决实际问题。
新课导入
思考
一辆匀速行驶的汽车在 11:20 距离 A 地 50 km,要在 12:00 之前驶过 A 地,车速满足什么条件?
这个问题我们要怎么解答呢?
A
50千米
11 :20
12 :00
40分钟=2/3小时
新知探究
下列问题中的数量关系能用等式表示吗?若不能,应该用怎样的式子来表示
(1)下图为公路上对汽车的限速标志,表示汽车在该路段行使的速度不得超过40Km/h,用v(km/h)表示汽车的速度,怎样表示v和40之间的关系
v≤40
(2)根据科学家测定,太阳表面的温度不低于6000℃.设太阳表面的温度为t (℃),怎样表示t与6000之间的关系?
t≥6000
新知探究
下列问题中的数量关系能用等式表示吗?若不能,应该用怎样的式子来表示
(3)如图,天平左盘放3个的乒乓球,右盘放5g砝码,天平倾斜,设每个乒乓球的质量为x(g),怎样表示x与5之间的关系?
3x > 5
(4)如图,小聪与小明玩跷跷板,两人都不用力时,跷跷板左低、右高,小聪的身体质量为p (kg),书包的质量为2kg,小明的身体质量为q (kg),怎样表示p , q之间的关系
q<2+p
新知探究
下列问题中的数量关系能用等式表示吗?若不能,应该用怎样的式子来表示
(5)要使代数式 有意义,x的值与3之间有什么关系?
x≠3
新知讲解
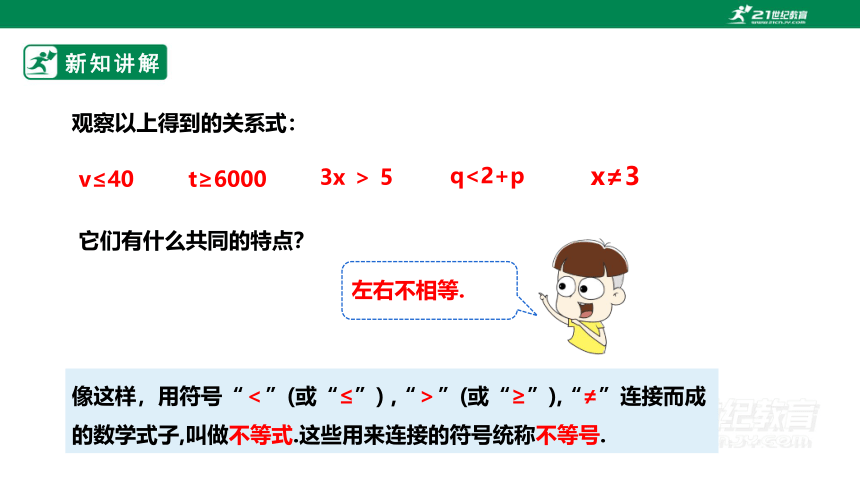
观察以上得到的关系式:
左右不相等.
它们有什么共同的特点?
像这样,用符号“<”(或“≤”) ,“>”(或“≥”),“≠”连接而成的数学式子,叫做不等式.这些用来连接的符号统称不等号.
v≤40
t≥6000
3x > 5
q<2+p
x≠3
新知讲解
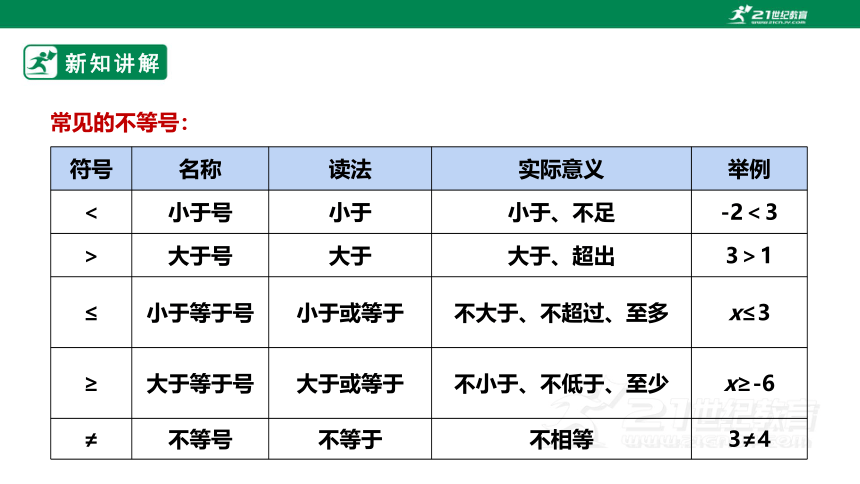
常见的不等号:
符号 名称 读法 实际意义 举例
< 小于号 小于 小于、不足 -2<3
> 大于号 大于 大于、超出 3>1
≤ 小于等于号 小于或等于 不大于、不超过、至多 x≤3
≥ 大于等于号 大于或等于 不小于、不低于、至少 x≥-6
≠ 不等号 不等于 不相等 3≠4
新知讲解
例1 根据下列数量关系列不等式:
(1)a是正数;
(2)y的2倍与6的和比1小;
(3)x2减去10不大于10;
(4)设a,b,c为一个三角形的三条边长,两边之和大于第三边.
a>0
a+b>c a+c>b b+c>a
x2-10≤10
2y+6<1
针对训练
①a是正数; ②a是负数;
③a与5的和小于7; ④a与2的差大于-1;
⑤a的4倍大于8; ⑥a的一半小于3.
①a>0; ②a<0; ③a+5<7;
④a – 2>– 1 ; ⑤4a>8; ⑥ a<3.
解:
用不等式表示:
新知探究
【做一做】
①已知x1=1,x2=2,请在数轴上表示出x1,x2的位置;
2
1
0
-1
x1
x2
②x<1表示怎样的数的全体?
(表示所有比1小的数的全体.)
2
1
0
-1
x≥2表示怎样的数的全体?
(表示所有大于等于2的数的全体.)
2
1
0
-1
新知讲解
x<a表示小于a的全体实数,在数轴上对应a左边的所有点,不包括a在内;
x≥a表示大于或等于a的全体实数,在数轴上对应a右边的所有点,包括a在内;
b<x<a(b<a)表示大于b而小于a的全体实数,在数轴上对应如图。
新知讲解
a
a
a
b
在数轴上表示出以下的不等式.
(1) x>a
(2) x≤a
(3) b ≤ x<a (b < a)
a
a
b
a
新知讲解
不等式 x > a x < a x ≥ a x ≤ a
数轴表示
用数轴表示不等式的步骤:
1.定边界点:在数轴上要标出原点和边界点,注意是实心圆点还是空心圆圈,有等号边界点画实心圆点(表示包括这一点),无等号边界点画空心圆圈(表示不包括这一点).
2.定方向:大于向右,小于向左.
0
a
0
a
0
a
0
a
常见不等式在数轴上的表示:
新知讲解
例2 一座小水电站的水库水位在12~20m(包括12m,20m)时,
发电机能正常工作.设水库水位为x(m).
(1)用不等式表示发电机正常工作的水位范围,并把它表示在数轴上;
(2)当水位在下列位置时,发电机能正常工作吗?
①x1=8;②x2=10;③x3=15;④x4=19.
用不等式和数轴给出解释。
新知讲解
解:(1)正常工作范围 12≤x≤20.
0
2
4
6
8
10
12
14
16
18
20
22
x2
x1
x3
x4
显然, x3,x4满足不等式12≤x≤20 ,而x1,x2不满足,
当水位在15m,19m时,发电机能正常发电,
当水位在8m,10m时,发电机不能正常发电。
0
2
4
6
8
10
12
14
16
18
20
22
(2)
问题解答
分析:
设车速是 x 千米/时.
从时间上看
汽车要在 12:00 之前驶过 A 地,则以这个速度行驶 50 km 所用的时间不到 h,即:
从路程上看
汽车要在 12:00 之前驶过 A 地,则以这个速度行驶 h 的路程要超过 50 km,即:
本节导入问题解答:
1.下列式子:①a+b=b+a;②-3>-5;③x≠1;④x+3>6;⑤2m<n;⑥2x-3,其中不等式有( )
A.2个 B.3个 C.4个 D.5个
2.某市最高气温是33℃,最低气温是24℃,则该市气温t(℃)的变化范围是( )
A.t>33 B.t≤24
C.24<t<33 D.24≤t≤33
C
D
课堂练习
课堂练习
3.下列数量关系用不等式表示错误的是( )
A.若a是负数,则a<0
B.若m的值小于1,则m<1
C.若x与-1的和大于0,则x-1>0
D.若a的 大于b,则 a≠b
D
课堂练习
4.实数a,b在数轴上的位置如图所示,选择适当的不等号填空。
>
>
<
<
<
课堂练习
5.恩格尔系数n是指家庭日常饮食占家庭总支出的比例,它反映了居民家庭的实际生活水平,各种类型家庭的n值如下表所示:
家庭类型 贫困 温饱 小康 发达国家 最富裕国家
n 75%以上 50%~75% 40%~49% 20%~39% 不到20%
如果用含n的不等式表示,那么贫困家庭为________,最富裕国家家庭为__________;当某一家庭n=0.6时,表明该家庭的实际生活水平是______.
n>75%
n<20%
温饱
课堂总结
一个概念:
备好数轴找准点
分清空实定方向
不等式(用“>、≥、<、≤、≠”连接)
列
表
抓住关键词,选准不等号。
两种步骤
三种思想:
数学建模、数形结合、分类讨论
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.1 认识不等式
浙教版 八年级上册
教学目标
【教学目标】
1.了解不等式的意义,经历由具体实例建立不等式模型的过程。
2.了解不等号的意义。
3.会根据给定的条件列不等式。
【重点】不等式的概念和列不等式。
【难点】既要理解不等式的意义,又要会在数轴上表示,并用来解决实际问题。
新课导入
思考
一辆匀速行驶的汽车在 11:20 距离 A 地 50 km,要在 12:00 之前驶过 A 地,车速满足什么条件?
这个问题我们要怎么解答呢?
A
50千米
11 :20
12 :00
40分钟=2/3小时
新知探究
下列问题中的数量关系能用等式表示吗?若不能,应该用怎样的式子来表示
(1)下图为公路上对汽车的限速标志,表示汽车在该路段行使的速度不得超过40Km/h,用v(km/h)表示汽车的速度,怎样表示v和40之间的关系
v≤40
(2)根据科学家测定,太阳表面的温度不低于6000℃.设太阳表面的温度为t (℃),怎样表示t与6000之间的关系?
t≥6000
新知探究
下列问题中的数量关系能用等式表示吗?若不能,应该用怎样的式子来表示
(3)如图,天平左盘放3个的乒乓球,右盘放5g砝码,天平倾斜,设每个乒乓球的质量为x(g),怎样表示x与5之间的关系?
3x > 5
(4)如图,小聪与小明玩跷跷板,两人都不用力时,跷跷板左低、右高,小聪的身体质量为p (kg),书包的质量为2kg,小明的身体质量为q (kg),怎样表示p , q之间的关系
q<2+p
新知探究
下列问题中的数量关系能用等式表示吗?若不能,应该用怎样的式子来表示
(5)要使代数式 有意义,x的值与3之间有什么关系?
x≠3
新知讲解
观察以上得到的关系式:
左右不相等.
它们有什么共同的特点?
像这样,用符号“<”(或“≤”) ,“>”(或“≥”),“≠”连接而成的数学式子,叫做不等式.这些用来连接的符号统称不等号.
v≤40
t≥6000
3x > 5
q<2+p
x≠3
新知讲解
常见的不等号:
符号 名称 读法 实际意义 举例
< 小于号 小于 小于、不足 -2<3
> 大于号 大于 大于、超出 3>1
≤ 小于等于号 小于或等于 不大于、不超过、至多 x≤3
≥ 大于等于号 大于或等于 不小于、不低于、至少 x≥-6
≠ 不等号 不等于 不相等 3≠4
新知讲解
例1 根据下列数量关系列不等式:
(1)a是正数;
(2)y的2倍与6的和比1小;
(3)x2减去10不大于10;
(4)设a,b,c为一个三角形的三条边长,两边之和大于第三边.
a>0
a+b>c a+c>b b+c>a
x2-10≤10
2y+6<1
针对训练
①a是正数; ②a是负数;
③a与5的和小于7; ④a与2的差大于-1;
⑤a的4倍大于8; ⑥a的一半小于3.
①a>0; ②a<0; ③a+5<7;
④a – 2>– 1 ; ⑤4a>8; ⑥ a<3.
解:
用不等式表示:
新知探究
【做一做】
①已知x1=1,x2=2,请在数轴上表示出x1,x2的位置;
2
1
0
-1
x1
x2
②x<1表示怎样的数的全体?
(表示所有比1小的数的全体.)
2
1
0
-1
x≥2表示怎样的数的全体?
(表示所有大于等于2的数的全体.)
2
1
0
-1
新知讲解
x<a表示小于a的全体实数,在数轴上对应a左边的所有点,不包括a在内;
x≥a表示大于或等于a的全体实数,在数轴上对应a右边的所有点,包括a在内;
b<x<a(b<a)表示大于b而小于a的全体实数,在数轴上对应如图。
新知讲解
a
a
a
b
在数轴上表示出以下的不等式.
(1) x>a
(2) x≤a
(3) b ≤ x<a (b < a)
a
a
b
a
新知讲解
不等式 x > a x < a x ≥ a x ≤ a
数轴表示
用数轴表示不等式的步骤:
1.定边界点:在数轴上要标出原点和边界点,注意是实心圆点还是空心圆圈,有等号边界点画实心圆点(表示包括这一点),无等号边界点画空心圆圈(表示不包括这一点).
2.定方向:大于向右,小于向左.
0
a
0
a
0
a
0
a
常见不等式在数轴上的表示:
新知讲解
例2 一座小水电站的水库水位在12~20m(包括12m,20m)时,
发电机能正常工作.设水库水位为x(m).
(1)用不等式表示发电机正常工作的水位范围,并把它表示在数轴上;
(2)当水位在下列位置时,发电机能正常工作吗?
①x1=8;②x2=10;③x3=15;④x4=19.
用不等式和数轴给出解释。
新知讲解
解:(1)正常工作范围 12≤x≤20.
0
2
4
6
8
10
12
14
16
18
20
22
x2
x1
x3
x4
显然, x3,x4满足不等式12≤x≤20 ,而x1,x2不满足,
当水位在15m,19m时,发电机能正常发电,
当水位在8m,10m时,发电机不能正常发电。
0
2
4
6
8
10
12
14
16
18
20
22
(2)
问题解答
分析:
设车速是 x 千米/时.
从时间上看
汽车要在 12:00 之前驶过 A 地,则以这个速度行驶 50 km 所用的时间不到 h,即:
从路程上看
汽车要在 12:00 之前驶过 A 地,则以这个速度行驶 h 的路程要超过 50 km,即:
本节导入问题解答:
1.下列式子:①a+b=b+a;②-3>-5;③x≠1;④x+3>6;⑤2m<n;⑥2x-3,其中不等式有( )
A.2个 B.3个 C.4个 D.5个
2.某市最高气温是33℃,最低气温是24℃,则该市气温t(℃)的变化范围是( )
A.t>33 B.t≤24
C.24<t<33 D.24≤t≤33
C
D
课堂练习
课堂练习
3.下列数量关系用不等式表示错误的是( )
A.若a是负数,则a<0
B.若m的值小于1,则m<1
C.若x与-1的和大于0,则x-1>0
D.若a的 大于b,则 a≠b
D
课堂练习
4.实数a,b在数轴上的位置如图所示,选择适当的不等号填空。
>
>
<
<
<
课堂练习
5.恩格尔系数n是指家庭日常饮食占家庭总支出的比例,它反映了居民家庭的实际生活水平,各种类型家庭的n值如下表所示:
家庭类型 贫困 温饱 小康 发达国家 最富裕国家
n 75%以上 50%~75% 40%~49% 20%~39% 不到20%
如果用含n的不等式表示,那么贫困家庭为________,最富裕国家家庭为__________;当某一家庭n=0.6时,表明该家庭的实际生活水平是______.
n>75%
n<20%
温饱
课堂总结
一个概念:
备好数轴找准点
分清空实定方向
不等式(用“>、≥、<、≤、≠”连接)
列
表
抓住关键词,选准不等号。
两种步骤
三种思想:
数学建模、数形结合、分类讨论
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
