浙教版八年级数学上册 第一章三角形的初步知识单元练习(含答案)
文档属性
| 名称 | 浙教版八年级数学上册 第一章三角形的初步知识单元练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 92.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-08 17:02:06 | ||
图片预览

文档简介
浙教版八年级数学上册第一章三角形的初步知识单元练习(附答案)
一、单选题(每题3分,共30分)(共10题;共30分)
1.已知三角形的三边分别为2、a、4,那么a的取值范围是
A. B. C. D.
2.下列命题中,真命题是( )
A.若 =2 ,则AB=2CD
B.平分弦的直径垂直于弦,且平分弦所对的两条弧
C.直径所对的圆周角是直角
D.同一条弧所对的圆心角等于它所对圆周角的一半
3.下列语句是命题的是( )
⑴两点之间,线段最短;(2)如果两个角的和是90度,那么这两个角互余. (3)请画出两条互相平行的直线;(4)过直线外一点作已知直线的垂线;
A.(1)(2) B.(3)(4) C.(2)(3) D.(1)(4)
4.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为( )
A.3 B.4 C.5 D.6
5.已知图中的两个三角形全等,则∠α等于( )
A.72° B.60° C.58° D.48°
6.在中,,的角平分线AD交BC于点D,CD=2,则点D到AB的距离是 ( )
A.1 B.2 C.3 D.4
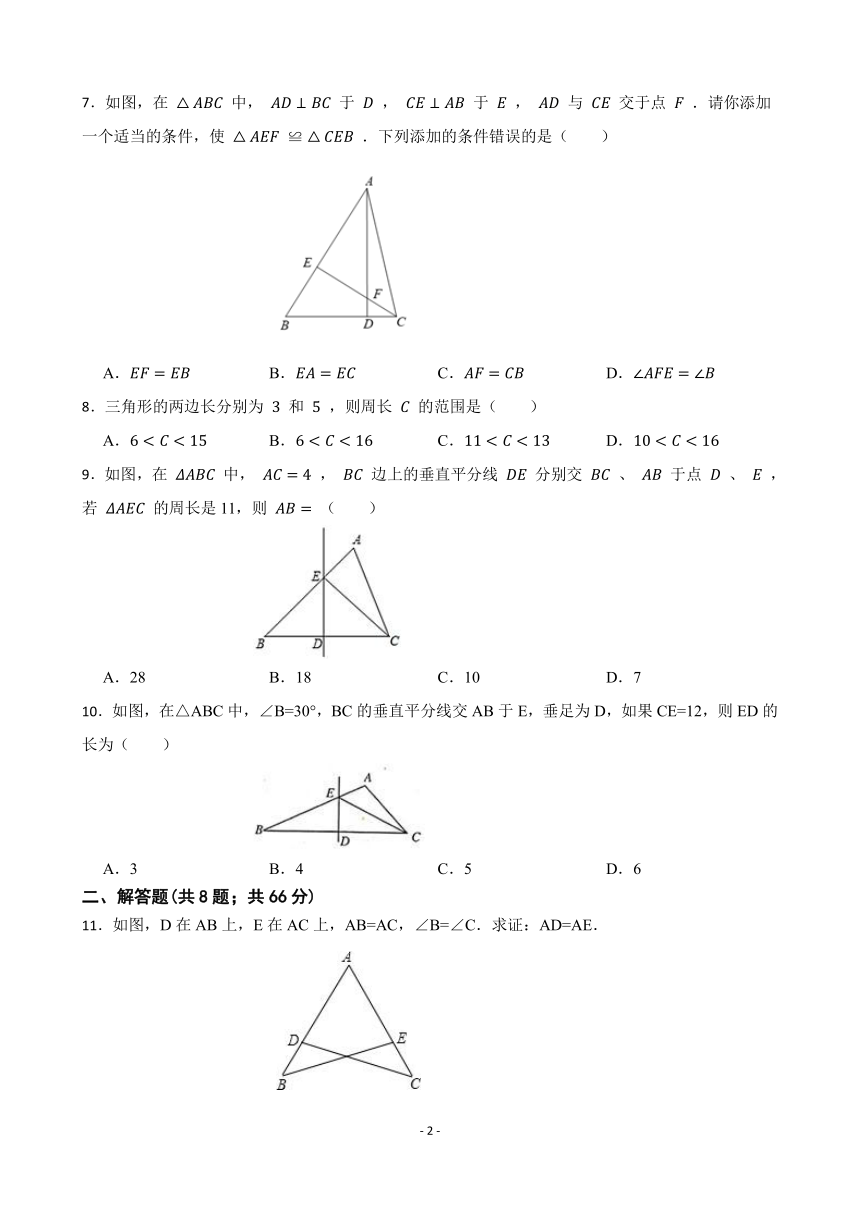
7.如图,在 中, 于 , 于 , 与 交于点 .请你添加一个适当的条件,使 ≌ .下列添加的条件错误的是( )
A. B. C. D.
8.三角形的两边长分别为 和 ,则周长 的范围是( )
A. B. C. D.
9.如图,在 中, , 边上的垂直平分线 分别交 、 于点 、 ,若 的周长是11,则 ( )
A.28 B.18 C.10 D.7
10.如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D,如果CE=12,则ED的长为( )
A.3 B.4 C.5 D.6
二、解答题(共8题;共66分)
11.如图,D在AB上,E在AC上,AB=AC,∠B=∠C.求证:AD=AE.
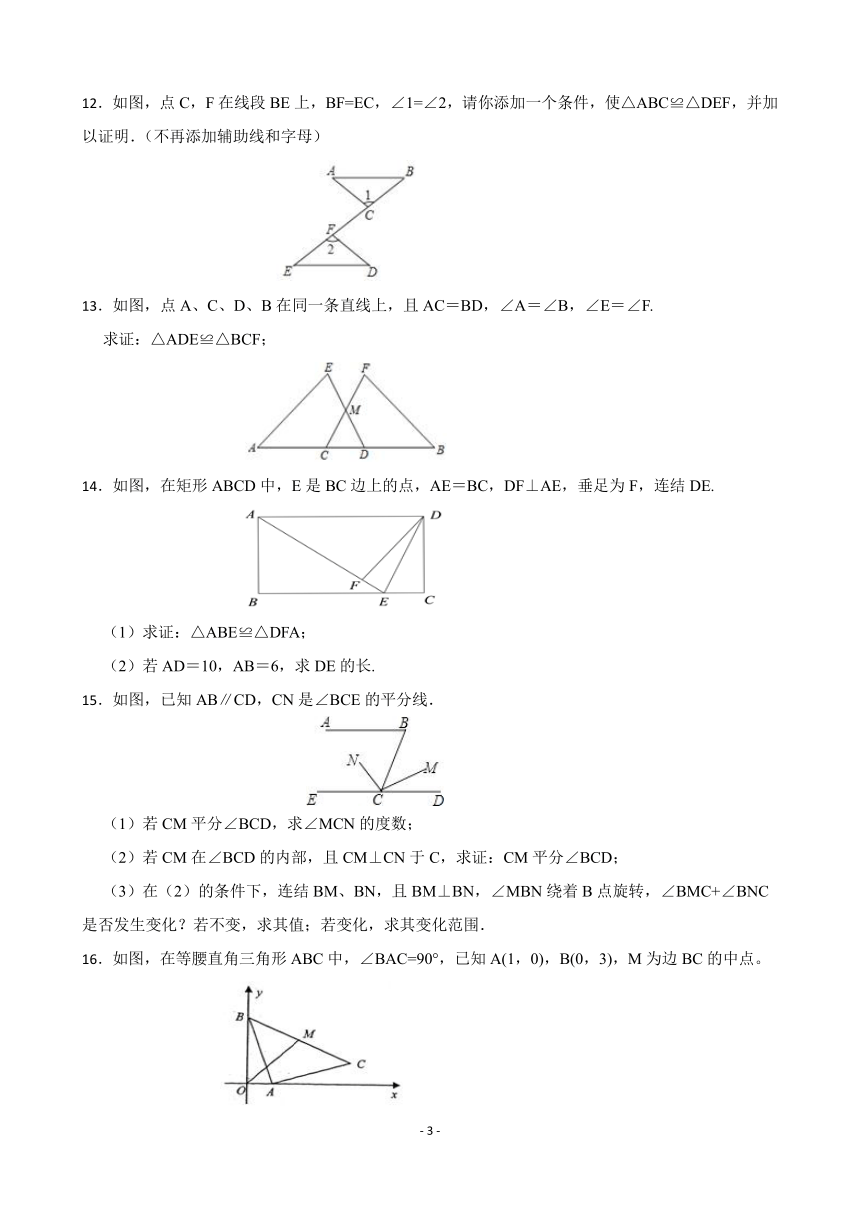
12.如图,点C,F在线段BE上,BF=EC,∠1=∠2,请你添加一个条件,使△ABC≌△DEF,并加以证明.(不再添加辅助线和字母)
13.如图,点A、C、D、B在同一条直线上,且AC=BD,∠A=∠B,∠E=∠F.
求证:△ADE≌△BCF;
14.如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连结DE.
(1)求证:△ABE≌△DFA;
(2)若AD=10,AB=6,求DE的长.
15.如图,已知AB∥CD,CN是∠BCE的平分线.
(1)若CM平分∠BCD,求∠MCN的度数;
(2)若CM在∠BCD的内部,且CM⊥CN于C,求证:CM平分∠BCD;
(3)在(2)的条件下,连结BM、BN,且BM⊥BN,∠MBN绕着B点旋转,∠BMC+∠BNC是否发生变化?若不变,求其值;若变化,求其变化范围.
16.如图,在等腰直角三角形ABC中,∠BAC=90°,已知A(1,0),B(0,3),M为边BC的中点。
(1)求点C的坐标;
(2)设点M的坐标为(a,b),求 的值;
(3)探究:在x轴上是否存在点P,使以O、P、M为顶点的三角形与△OBM相似?若存在,请求出点P的坐标:若不存在,请简述理由。
17.如图,点O是直线AB上的一点,∠BOC:∠AOC=1:2,OD平分∠BOC,OE⊥OD于点O.
(1)求∠BOC的度数;
(2)试说明OE平分∠AOC.
18.如图,AC平分∠BAD,CR⊥AB,CD⊥AD,点B、D为垂足,CF=CB。
(1)求证:BE= FD:
(2)若CD=6,AD=8,求四边形ABCF的面积。
答案
1.B 2.C 3.A 4.A 5.D 6.B 7.D 8.D 9.D 10.D
11.解:在△ABE与△ACD中, ,
∴△ACD≌△ABE(ASA),
∴AD=AE(全等三角形的对应边相等).
12.解:AC=DF.
证明:∵BF=EC,
∴BF﹣CF=EC﹣CF,∴BC=EF,
在△ABC和△DEF中
∴△ABC≌△DEF(SAS).
13.证明: , , ,
,
在 和 中, , .
14.(1)证明: 在矩形 中, ,
.
, , .
(AAS).
(2)解:由(1)知 . .
在直角 中, ,
.
在Rt 中, ,
15.(1)解:∵CN、CM分别平分∠BCE和∠BCD,
∴ , ,
∵∠BCE+∠BCD=180°,
∴∠MCN=∠BCN+∠BCM= = (∠BCE+∠BCD)=90°;
(2)证明:∵CM⊥CN, ∴∠MCN=90°,
即∠BCN+∠BCM=90°,∴2∠BCN+2∠BCM=180°,
∵CN是∠BCE的平分线,
∴∠BCE=2∠BCN,∴∠BCE+2∠BCM=180°,
∴∠BCD=2∠BCM,∴CM平分∠BCD;
(3)解:如图,∠BMC+∠BNC=180°,
延长AB至F,过N,M分别作NG∥AB,MH∥AB,则有NG∥AB∥MH∥CD,
∴∠BNG=∠ABN,∠CNG=∠ECN,∠BMH=∠FBM,∠CMH=∠DCM,
∵BM⊥BN,CM⊥CN,
∴∠MBN=∠MCN=90°,
∵∠ABN+∠MBN+∠FBN=180°,∠ECN+∠MCN+∠DCM=180°,
∴∠ABN+∠FBM+∠ECN+∠DCM=180°,
∴∠BMC+∠BNC=∠BMH+∠CMH+∠BNG+∠CNG=∠ABN+∠FBM+∠ECN+∠DCM=180°,
∴∠BMC+∠BNC=180°不变.
16.(1)解:过点C作CD⊥x轴,垂足为点D
∵△ABC是等腰直角三角形,∴AB=CA,∠BAC=90°,∴∠OAB+∠CAD=90°,
又∠OAB+∠ABO=90°
∴∠ABO=∠CAD,
∵∠AOB=∠CDA,∴△ABO≌△CAD
∴AO=CD=1,OB=AD=3,∴C(4,1)
(2)解:过点M作MH⊥x轴,垂足为点H
∵BO∥MH∥CD,MB=MC ∴a=HO=HD=2
∴b=MH =2,∴ =1
(3)解:存在点P,分三种情况:
∵在Rt△OMH中,∵MH=OH=2,∴∠MOH=45°
当点P在x轴时,∵∠MOP=45°=∠BOM,∴当△CBD∽△CAB时,有 或
∴OP=3或OP= ∴P1(3,0)、P2( ,0)
17.(1)解:∵∠AOB=∠BOC+∠AOC=180°,
又∠BOC:∠AOC=1:2,
∴∠AOC=2∠BOC,
∴∠BOC+2∠BOC=180°,
∴∠BOC=60°;
(2)解:∵OD平分∠BOC, ∴∠BOD=∠DOC,
∵∠DOC+∠COE=90°,∠AOB是平角,
∴∠AOE+∠BOD=90°,∴∠AOE=∠COE
即OE平分∠AOC.
18.(1)证明:∵AC平分 , ,
∴
又∵CF=CB∴ ≌ ∴BE=FD
(2)解:∵ , , ,
∴ ≌
又∵ ≌ ,CD=6,AD=8
∴
一、单选题(每题3分,共30分)(共10题;共30分)
1.已知三角形的三边分别为2、a、4,那么a的取值范围是
A. B. C. D.
2.下列命题中,真命题是( )
A.若 =2 ,则AB=2CD
B.平分弦的直径垂直于弦,且平分弦所对的两条弧
C.直径所对的圆周角是直角
D.同一条弧所对的圆心角等于它所对圆周角的一半
3.下列语句是命题的是( )
⑴两点之间,线段最短;(2)如果两个角的和是90度,那么这两个角互余. (3)请画出两条互相平行的直线;(4)过直线外一点作已知直线的垂线;
A.(1)(2) B.(3)(4) C.(2)(3) D.(1)(4)
4.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为( )
A.3 B.4 C.5 D.6
5.已知图中的两个三角形全等,则∠α等于( )
A.72° B.60° C.58° D.48°
6.在中,,的角平分线AD交BC于点D,CD=2,则点D到AB的距离是 ( )
A.1 B.2 C.3 D.4
7.如图,在 中, 于 , 于 , 与 交于点 .请你添加一个适当的条件,使 ≌ .下列添加的条件错误的是( )
A. B. C. D.
8.三角形的两边长分别为 和 ,则周长 的范围是( )
A. B. C. D.
9.如图,在 中, , 边上的垂直平分线 分别交 、 于点 、 ,若 的周长是11,则 ( )
A.28 B.18 C.10 D.7
10.如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D,如果CE=12,则ED的长为( )
A.3 B.4 C.5 D.6
二、解答题(共8题;共66分)
11.如图,D在AB上,E在AC上,AB=AC,∠B=∠C.求证:AD=AE.
12.如图,点C,F在线段BE上,BF=EC,∠1=∠2,请你添加一个条件,使△ABC≌△DEF,并加以证明.(不再添加辅助线和字母)
13.如图,点A、C、D、B在同一条直线上,且AC=BD,∠A=∠B,∠E=∠F.
求证:△ADE≌△BCF;
14.如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连结DE.
(1)求证:△ABE≌△DFA;
(2)若AD=10,AB=6,求DE的长.
15.如图,已知AB∥CD,CN是∠BCE的平分线.
(1)若CM平分∠BCD,求∠MCN的度数;
(2)若CM在∠BCD的内部,且CM⊥CN于C,求证:CM平分∠BCD;
(3)在(2)的条件下,连结BM、BN,且BM⊥BN,∠MBN绕着B点旋转,∠BMC+∠BNC是否发生变化?若不变,求其值;若变化,求其变化范围.
16.如图,在等腰直角三角形ABC中,∠BAC=90°,已知A(1,0),B(0,3),M为边BC的中点。
(1)求点C的坐标;
(2)设点M的坐标为(a,b),求 的值;
(3)探究:在x轴上是否存在点P,使以O、P、M为顶点的三角形与△OBM相似?若存在,请求出点P的坐标:若不存在,请简述理由。
17.如图,点O是直线AB上的一点,∠BOC:∠AOC=1:2,OD平分∠BOC,OE⊥OD于点O.
(1)求∠BOC的度数;
(2)试说明OE平分∠AOC.
18.如图,AC平分∠BAD,CR⊥AB,CD⊥AD,点B、D为垂足,CF=CB。
(1)求证:BE= FD:
(2)若CD=6,AD=8,求四边形ABCF的面积。
答案
1.B 2.C 3.A 4.A 5.D 6.B 7.D 8.D 9.D 10.D
11.解:在△ABE与△ACD中, ,
∴△ACD≌△ABE(ASA),
∴AD=AE(全等三角形的对应边相等).
12.解:AC=DF.
证明:∵BF=EC,
∴BF﹣CF=EC﹣CF,∴BC=EF,
在△ABC和△DEF中
∴△ABC≌△DEF(SAS).
13.证明: , , ,
,
在 和 中, , .
14.(1)证明: 在矩形 中, ,
.
, , .
(AAS).
(2)解:由(1)知 . .
在直角 中, ,
.
在Rt 中, ,
15.(1)解:∵CN、CM分别平分∠BCE和∠BCD,
∴ , ,
∵∠BCE+∠BCD=180°,
∴∠MCN=∠BCN+∠BCM= = (∠BCE+∠BCD)=90°;
(2)证明:∵CM⊥CN, ∴∠MCN=90°,
即∠BCN+∠BCM=90°,∴2∠BCN+2∠BCM=180°,
∵CN是∠BCE的平分线,
∴∠BCE=2∠BCN,∴∠BCE+2∠BCM=180°,
∴∠BCD=2∠BCM,∴CM平分∠BCD;
(3)解:如图,∠BMC+∠BNC=180°,
延长AB至F,过N,M分别作NG∥AB,MH∥AB,则有NG∥AB∥MH∥CD,
∴∠BNG=∠ABN,∠CNG=∠ECN,∠BMH=∠FBM,∠CMH=∠DCM,
∵BM⊥BN,CM⊥CN,
∴∠MBN=∠MCN=90°,
∵∠ABN+∠MBN+∠FBN=180°,∠ECN+∠MCN+∠DCM=180°,
∴∠ABN+∠FBM+∠ECN+∠DCM=180°,
∴∠BMC+∠BNC=∠BMH+∠CMH+∠BNG+∠CNG=∠ABN+∠FBM+∠ECN+∠DCM=180°,
∴∠BMC+∠BNC=180°不变.
16.(1)解:过点C作CD⊥x轴,垂足为点D
∵△ABC是等腰直角三角形,∴AB=CA,∠BAC=90°,∴∠OAB+∠CAD=90°,
又∠OAB+∠ABO=90°
∴∠ABO=∠CAD,
∵∠AOB=∠CDA,∴△ABO≌△CAD
∴AO=CD=1,OB=AD=3,∴C(4,1)
(2)解:过点M作MH⊥x轴,垂足为点H
∵BO∥MH∥CD,MB=MC ∴a=HO=HD=2
∴b=MH =2,∴ =1
(3)解:存在点P,分三种情况:
∵在Rt△OMH中,∵MH=OH=2,∴∠MOH=45°
当点P在x轴时,∵∠MOP=45°=∠BOM,∴当△CBD∽△CAB时,有 或
∴OP=3或OP= ∴P1(3,0)、P2( ,0)
17.(1)解:∵∠AOB=∠BOC+∠AOC=180°,
又∠BOC:∠AOC=1:2,
∴∠AOC=2∠BOC,
∴∠BOC+2∠BOC=180°,
∴∠BOC=60°;
(2)解:∵OD平分∠BOC, ∴∠BOD=∠DOC,
∵∠DOC+∠COE=90°,∠AOB是平角,
∴∠AOE+∠BOD=90°,∴∠AOE=∠COE
即OE平分∠AOC.
18.(1)证明:∵AC平分 , ,
∴
又∵CF=CB∴ ≌ ∴BE=FD
(2)解:∵ , , ,
∴ ≌
又∵ ≌ ,CD=6,AD=8
∴
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
